基于共同因子法和阈值法的局部放电去噪方法
朱庆东,伊 锋,许 伟,高志新,徐 冉
(国网山东省电力公司电力科学研究院,山东 济南 250003)
0 引言
局部放电(Partial Discharge,PD)会使得电气设备的绝缘性能逐渐劣化,造成潜在的危险,严重时PD 还会造成设备停运。因此,为了准确评估设备绝缘状况,制定合理的检修计划,需要对电气设备进行PD在线监测[1-2]。在实际工程中,最常用的方法之一是特高频法,该方法通过特高频传感器来测量电磁波幅值来判断是否有PD 发生[3-4]。用特高频法进行PD 测量会受到现场随机噪声的影响,其中最常见的就是白噪声。为了得到真实的PD 信号,避免白噪声的影响,需要对测量信号进行去噪[5-6]。电力系统中常用的去噪方法是由Donoho 提出的基于小波变换的阈值去噪法。该方法是一种经典的去噪方法,具有普适性,被广泛应用于各类信号白噪声去噪问题。然而,该方法在应用过程中涉及下采样过程,导致小波变换缺乏平移不变性,从而造成混叠效应,影响结果精确性[7-8]。
为了克服缺乏平移不变性的缺陷,有学者提出非抽取小波变换(Non-decimation Wavelet Transform,NDWT)法,又称平稳小波变换(Stationary Wavelet Transform,SWT)法[9]。该方法没有下采样过程,保持了平移不变性质。但是由于该方法基于非正交变换,因此得到小波系数无法直接用阈值函数处理;学者Coifman 和Donoho 提出采用循环移位(Cycle Spinning,CS)的方法,将信号进行循环移位,并对移位后的信号全部进行去噪处理后再将均值作为输出信号[10]。该方法去噪精度更高,但是由于引入了循环移位,其计算耗时也远超基于小波变换的阈值去噪法。剑桥大学教授Kingsbury 指出,为了避免大量计算,同时尽量保持平移不变性[11-12],需要构造一个实部和虚部互相独立的复小波来对信号进行处理,此复小波也被称之为“双树复小波”(Dual-tree Complex Wavelet,DTCW)。在对信号进行处理时,用实部和虚部小波分别对信号进行阈值去噪,然后将两棵树的结果进行平均作为最终结果。学者Selesnick 从理论上推导出具有平移不变性的DTCW应满足的条件,同时提出一种共同因子法[13-17],即认为实部和虚部的小波函数都是由一个共同函数与另一个函数进行卷积而得到,通过该方法可以构造出近似满足平移不变性的DTCW。
PD 是一类非平稳时变信号,通常在时域上表现为指数衰减函数或高斯函数的形式。在前人研究结果的基础上,基于共同因子法构造出DTCW,进而利用邻近小波系数阈值法对PD 信号进行去噪。最后,对基准数据进行仿真计算,并与传统的去噪方法的结果进行了对比。
1 模型和基本原理
PD信号观测模型可以表示为
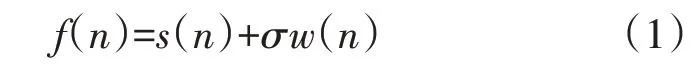
式中:(fn)为第n个观测信号;s(n)为真实PD 信号;w(n)为均值为0、标准差为1 的白噪声信号;σ为噪声标准差。
实际中常用的经典方法为阈值法,其基本原理是将信号进行小波分解,并对小波系数进行收缩,最后进行信号重构得到去噪信号。
1.1 信号分解
信号分解与重构是通过一组正交镜像滤波器函数(Quadrature Mirror Filter,QMF)h和g实现的。其中,h[·]称为尺度滤波器函数,g[·]称为小波滤波器函数。对信号进行y层分解,可得到各层逼近系数aj[p]和细节系数dj[p],其中j为系数所在层数,aj[p]和dj[p]为第j层第p个系数。分解公式如式(2)所示,该过程也被称为下采样过程[18]。
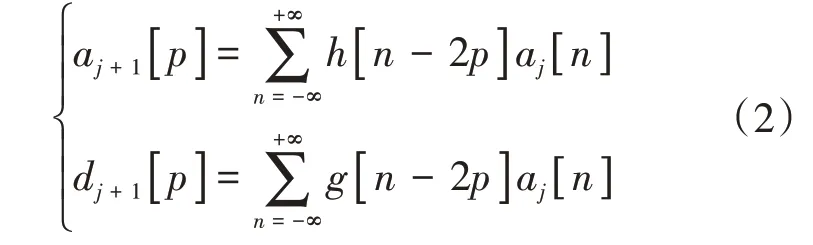
对得到的小波系数进行上采样过程可以得到重构信号,重构公式如式(3)所示。
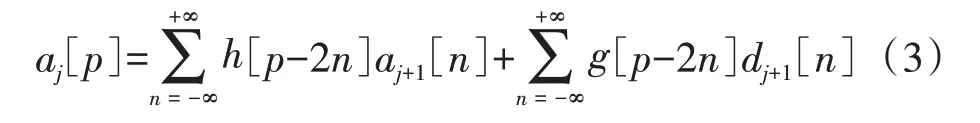
1.2 小波系数处理
对小波系数进行处理,首先需要根据细第y层细节系数dy,对白噪声信号的标准差σ进行估计。常用式(4)进行估算。

式中:fMAD为取中位数函数。
根据对标准差σ的估计值设定阈值λ,如最为常见的固定阈值λsqt为
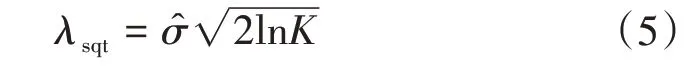
式中:K为小波系数个数。
将各层细节系数dj[p]乘以收缩系数,得到处理后的系数qj[p]。Donoho 提出用软阈值函数进行处理,为
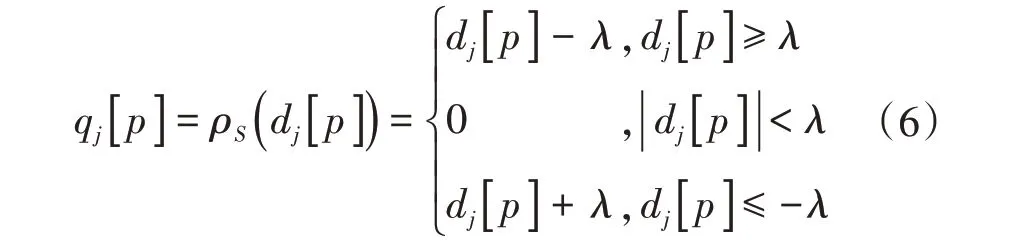
将处理过的小波系数qj进行重构,可得到去噪后的PD信号。
2 共同因子法
传统的基于小波变换阈值去噪方法中,式(2)是下采样过程,破坏了小波变换的平移不变性。于是信号剧烈变化部分会产生伪吉布斯现象,造成重构信号失真。为了克服缺乏平移不变性的缺陷,同时保证计算时长满足实际需求,学者N.Kingsbury 提出选择两个独立的实小波ψr和ψi分别作为DTCW 的实部和虚部,即ψc=ψr+ψi。对实部和虚部分别进行独立的小波变换阈值去噪后,将得到的结果求均值,即得到最终的重构信号。
文献[19-20]中,作者证明了若ψi=H{ψ}r,则DTCW 具有平移不变性,式中H{·}是Hilbert 变换。同时,构成Hilbert 变换对的ψr和ψi对应的尺度滤波器函数hi(n)和hr(n)在时域和z域应该分别满足条件为
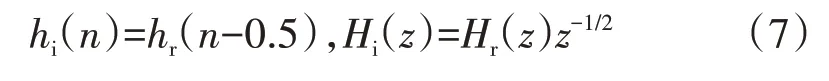
即实部树和虚部树之间应满足1/2 采样时延。由于hi(n)和hr(n)均为有限长单位冲激响应滤波器函数(Finite Impulse Response,FIR),因此该条件是无法满足的,所以只能通过某些构造手段来逼近。
在文献[13]中,Selesnick 提出具有特定形式的尺度滤波器函数hi(n)和hr(n)满足性质为
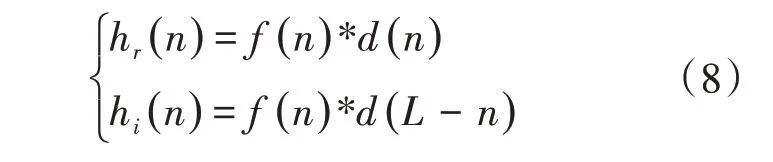
式中:*为卷积运算;L为某固定常数;d(n)为长度为L+1 的FIR;f(n)为滤波器函数hi(n)和hr(n)所包含的共同因子,因此该方法也被称为共同因子法。
将hi(n)和hr(n)变换到z域中可以得到
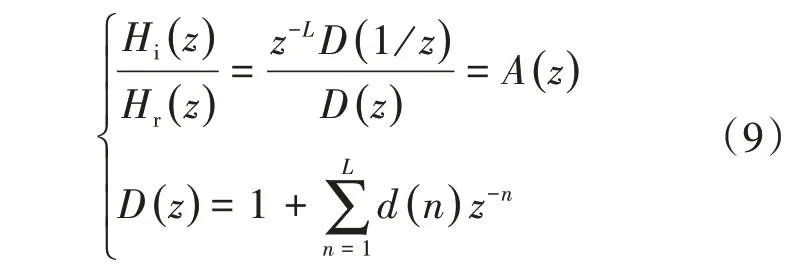
对比式(8)与式(9)可知,要逼近式(7),需要对d(n)的系数进行选择。Selesnick 证明了,当d(n)满足式(10)且取τ=1/2 时,式(9)可以在一定程度上逼近式(7),即A(z)≈z-1/2在z=1 附近成立。其中,τ应满足
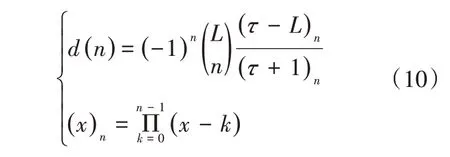
所以,在式(10)中取τ=1/2 即可获得近似构成Hilbert 变换对的DTCW。用类似于Daubechies 在文献[21]中提出的方法,最终可求出f(n)、hr(n)和hi(n)。
一个典型例子如表1所示,给定消失矩K=4,d(n)长度L=2,则实部和虚部滤波器函数hr(n)和hi(n)二者长度均为12,hr(n)和hi(n)的各项数值如表1所示。
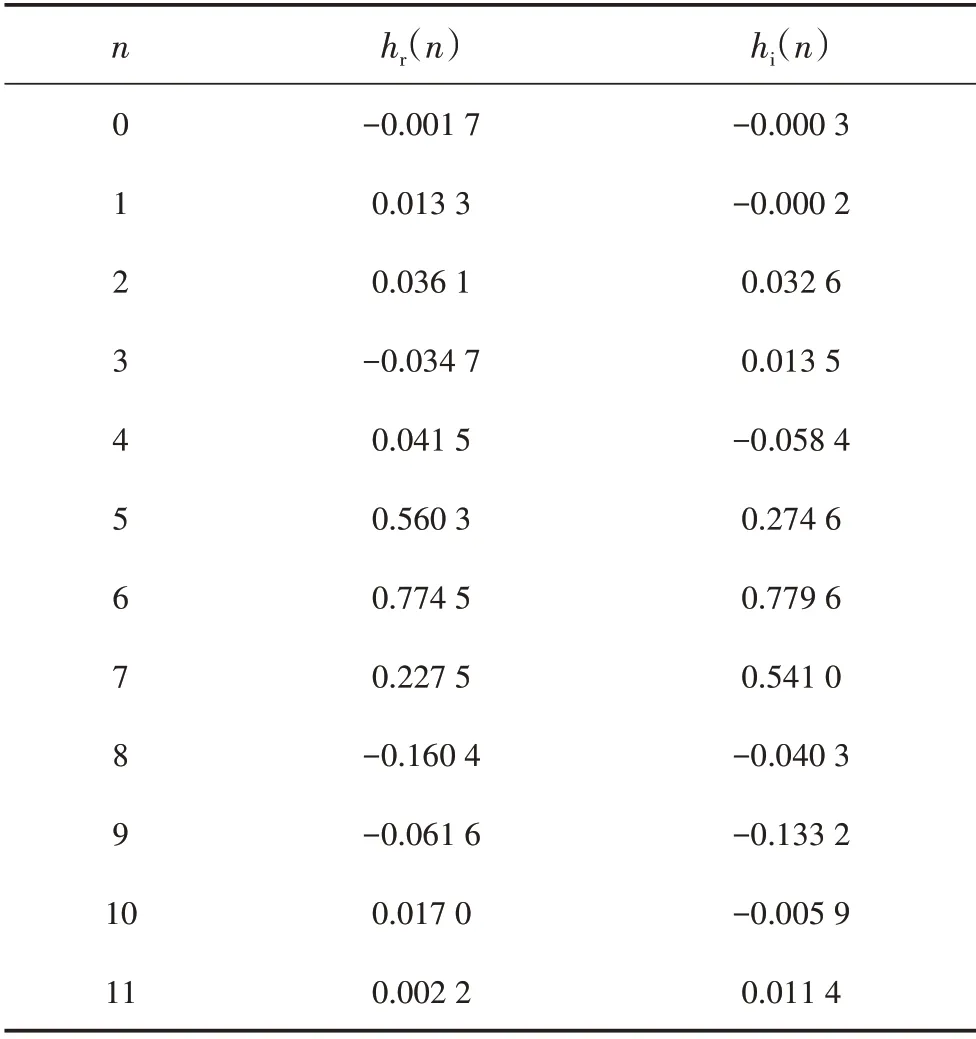
表1 h(rn)和h(in)各项数值
3 所提去噪算法
结合共同因子法和阈值去噪法,首先对含噪PD信号进行DTCW 变换,得到实部和虚部的小波系数,然后对两棵树进行基于邻近小波系数的阈值去噪,进而得到两棵树的重构信号,最后将两个信号进行平均得到最终结果,流程如图1所示。
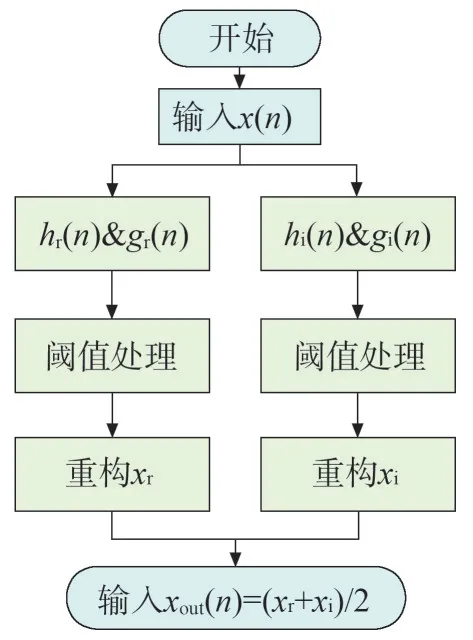
图1 算法流程
4 仿真算例验证
不同的电气设备有不同特征的特高频PD 信号。采用文献[22]所描述的PD 模型作为算例,即以SF6为介质的GIS 特高频气隙缺陷PD 信号模型。归一化的PD信号图像如图2所示。
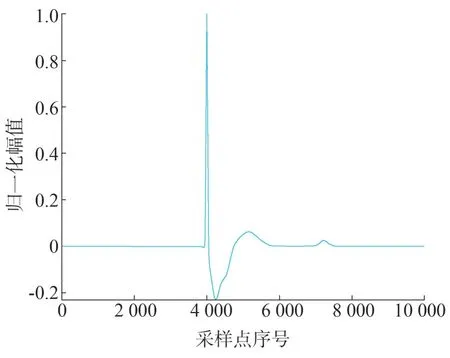
图2 PD信号
用构造的hi(n)和hr(n)来对含噪PD 信号进行分解,分解层数设为5 层,采用第3 节提出的去噪方法用固定阈值进行处理。同时作为对比,选择同样具有4 阶消失矩的DB4 小波,以及滤波器函数长度同样为12 的DB6 小波来进行计算。DB4/DB6 小波分解层数也设为5 层,采用固定阈值和软阈值函数进行处理。
为了评价去噪效果,引入了信噪比fSNR(Signal to Noise Ratio,SNR)和归一化相关系数fNCC(Normalized Correlation Coefficient,NCC)来对去噪效果进行评价。信噪比是用以衡量含噪PD 信号中信号与噪声能量比值的参数,其表达式为

而fNCC是用以衡量染噪PD 信号在去噪后与纯PD信号波形相似程度的参数,其表达式为

fSNR和fNCC二者数值越大,代表去噪效果越好。经过计算,所得fSNR和fNCC结果如图3 和图4 所示。其中横坐标代表噪声标准差,纵坐标代表fSNR/fNCC。
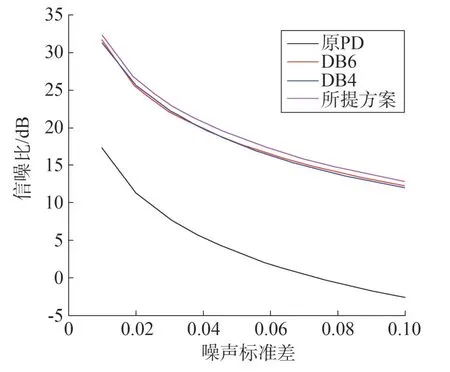
图3 PD信号去噪前后fSNR对比
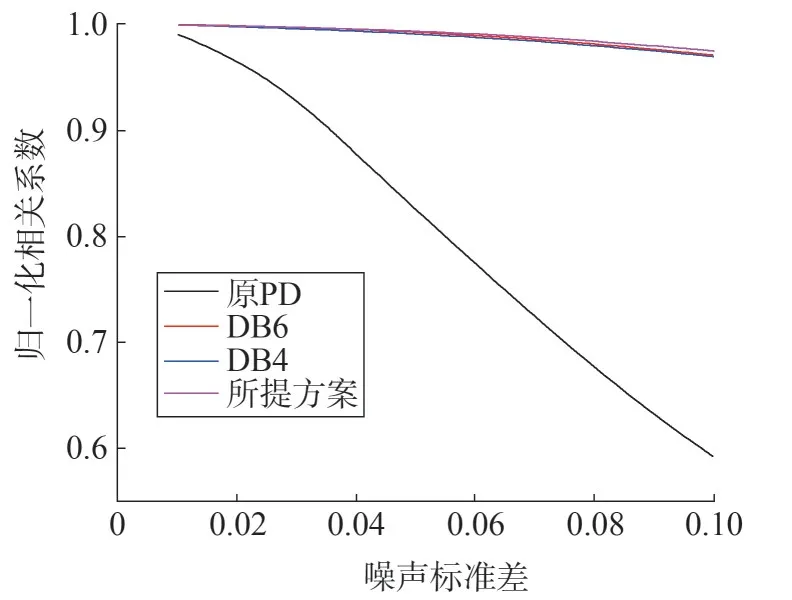
图4 PD信号去噪前后fNCC对比
根据计算结果可知,本文所提方法和DB4/DB6小波去噪都有较好的去噪效果,能够在很大程度上抑制信号中的噪声。但是,对于染噪PD 信号,无论原始染噪PD 信号的噪声强度高低,通过本文所提方法得到的fSNR和fNCC效果更优;同时,在噪声强度越高的情况下,本文所提方法去噪效果的优势越明显。
5 结语
基于共同因子法,构造出DTCW 组成近似Hilbert 变换对,并结合基于邻近小波系数的阈值去噪法,对被白噪声污染的PD 信号进行去噪。不同于传统的基于小波变换的阈值去噪法,提出了一种基于DTCW 变换的邻近小波系数阈值去噪法。在对被白噪声污染的特高频PD 信号进行处理时,所得结果表明本文所提方法得到的计算结果更为准确。

