基于Virtual.Lab的某电动车平顺性研究

史利芳， 杨 林， 刘进伟， 欧阳旭

(隆鑫通用动力股份有限公司 技术中心， 重庆 400039)

汽车行驶的平顺性主要指路面不平引起的汽车振动。研究平顺性的目的是控制汽车振动系统的动态特性，使系统输出的振动在一定范围内，对乘员舒适性或货物完整性的影响在一定界限之内。汽车平顺性作为主要指标之一，主要用于评价乘坐舒适性[1-5]，还影响到零部件及路面的疲劳寿命和行驶安全性。各主机厂、各研究机构和学者都将改善汽车平顺性作为研究重点，是提高中国汽车制造水平的关键因素。纵观国内外研究现状，各国学者和研究机构主要研究对象还是传统内燃机汽车，基于传统内燃机汽车的平顺性研究模型和相关理论已较为成熟，在电动汽车领域内的研究还相对较为欠缺。电动车以电机作为主要动力来源，因此路面激励引起的振动导致的汽车平顺性问题将作为主要的研究重点[6-8]。基于此，本文将两种不同频率的路面激励作为振动源，建立两种低频平顺性(1～5 Hz激励路面)和高频平顺性(5～25 Hz激励路面)作为平顺性评价工况，对整车底盘参数进行灵敏度分析，研究相关参数对平顺性的影响特性和影响程度，确定最终优化方案。

1 整车动力学模型

动力学主要研究作用于物体的力与物体运动的关系。车辆动力学模型一般用于分析车辆的平顺性和车辆的操纵稳定性。对于车辆来说，研究动力学主要研究车辆轮胎及其相关部件的受力情况。整车动力学模型的创建步骤包括建立车辆前悬架系统、后悬架系统、白车身、转向系统、驱动系统、轮胎等。车辆各个部件之间通过建立正确的连接关系如旋转副、衬套、TSDA、固定副等，保证车辆可以正常进行平顺性分析。

1.1 整车物理模型

实际汽车运动模型是一个融合了多自由度的复杂非线性系统，重建出完全符合其运动规律的物理模型极其困难。在实际研究过程中，根据研究重点的差异简化模型复杂性。在本文中做出以下假设：汽车沿纵向中心线左右对称，并作匀速直线运动，路面是平稳的，具有各向同性，考虑4个轮输入的相关性；路面以外的其他振源、轮胎阻尼暂不考虑[9]。

简化后的整车运动模型包含8个自由度，如图1所示，u、v、w、p分别为汽车的纵向速度、横向速度、横摆角速度和车身侧倾角速度，再加上4个车轮的转动角速度。图1中Fxi、Fyi、Fzi(i=1,2,3,4)为路面对车轮的作用力在车辆坐标系上的分解；C为整车质心；c′为簧载质量质心；h为整车质心距地面的高度；h′为簧载质心距离侧倾轴线的距离；T为汽车轮距；I为汽车轴距；a、b分别为整车质心至前、后轴的水平距离[9]。

图1 8自由度汽车动力学模型

1.2 建立整车动力学模型

采用LMS Virtual Lab软件中Motion模块(西门子工业软件公司，德国)建立整车动力学模型。主要包括柔性化的白车身、前悬架系统、柔性稳定杆、转向系统、后悬架系统、轮胎等，并且为了考虑路面激励是否会激励其他柔性零部件，对后桥、后横撑杆、后摇臂、前摇臂、车身、稳定杆等进行刚柔耦合分析。创建与电动车样车相符的整车动力学模型的整车动力学模型，如图2所示。

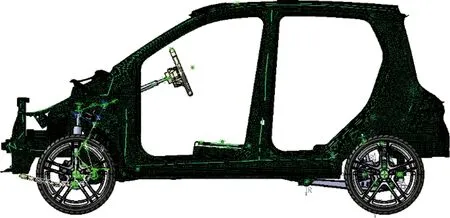
图2 整车动力学模型

1.3 模型校核

为保证分析结果的准确性，需对模型进行校核。本文主要通过整备状态前后各轮胎受力和整车自由模态的模型校核。为此对实车进行前/后悬架系统偏频试验，偏频是汽车底盘的前悬架和后悬架与簧上质量组成系统的固有频率，其大小和比值决定整车的平顺和操稳性能，故必须满足一定的标准。

偏频试验采用LMS Test Lab振动测试设备进行振动加速度信号采集。试验时首先将4个三向振动加速度传感器分别安装在2个后悬架的簧上位置和簧下位置，测试后轮冲击瞬间的振动信号，处理数据后得到左右后轮的偏频。校核结果见表1、表2。

通过对该车动力学模型进行校准，与试验结果误差在8%以内，判定动力学模型准确，可以进行平顺性分析。

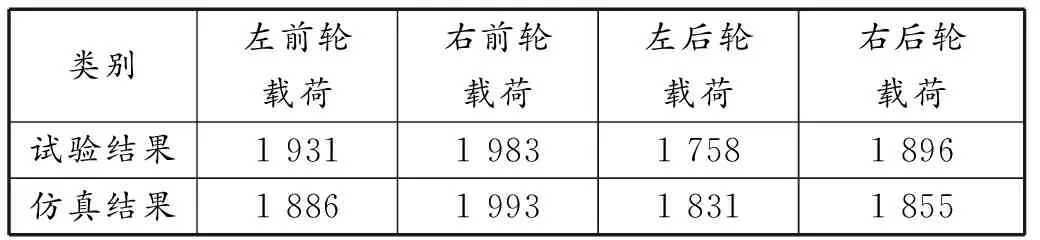
表1 载荷对比结果 单位：N

表2 偏频对比结果

2 评价工况与指标

2.1 评价工况

完成电动车动力学模型及校核后，平顺性研究中所使用的评价路况如图3所示，包括了平顺性研究的两种分析工况低频平顺性(Primary Ride)和高频平顺性(Secondary Ride)。

1)低频平顺性：低频振动(1～5 Hz)，竖直方向振动频率主要考虑1.0～1.2 Hz，俯仰频率主要考虑1.2～1.5 Hz，所有的车辆子系统可以被认为是一个刚体，主要考虑簧载质量相振动。

2)高频平顺性：中频振动(5～25 Hz)，涉及车身的结构振动振型(如汽车车架、簧下质量部件、柔性零部件、发动机的缸体模态的弯曲振型)，主要考虑非簧载质量振动。

针对平顺性分析的冲击工况，即高级振型(Harshness)：车辆结构和/或组件的更高频率振动(25～100 Hz),视为噪声分析工况，本文暂不考虑。

图3 评价路况

2.2 评价指标

传统平顺性评价方法以座椅、靠背、地板、方向盘等与人体直接接触的部位为检测点[1,10-15]，本文提出增加车身与底盘的8个连接点以及车身等检测点，能够更加全面地检测平顺性。

车身加速度均方根值是衡量汽车平顺性的常用指标，其大小直接影响乘员舒适性。本文以车身加速度均方根理论推导为例进行说明[1,4]。根据汽车理论可知，二自由度悬架振动模型为一线性模型，且当路面只有单个输入时，振动响应的PSD(功率谱密度)Gx(f)与路面位移输入PSD(功率谱密度)Gq(f)的关系式为

(1)

式中，|H(f)|x～q为系统输出x对输入q的幅频特性。

由于路面速度功率谱密度函数通常为“白噪声”，即在频域内为一常数。改写式(1)得

(2)

(3)

(4)

依据《人体承受全身振动计算 第一部分:一般要求》(ISO 2631-1)，人体对于不同方向上的振动频率敏感度不同。在垂直轴向方向，人体敏感频率为4～12.5 Hz，在4～8 Hz频率范围内，车身会与人体内脏器官产生共振，其频率为8～12.5 Hz。车身振动会对人的脊椎系统产生严重不良影响。所以，可以进一步研究考虑加权加速度均方根值作为评价指标时的情况[15]。对于垂向振动的频率f加权函数w(f)表示为

(5)

考虑频率加权函数的加权加速度均方根，其表达式[1,14]为

(6)

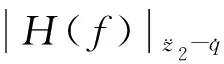
评价指标为RMS(均方根值)、RFG(原始信号的频域均方根值)、RMQ(均四次方根值)，计算式分别为

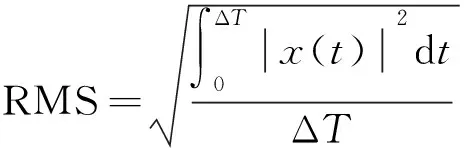
(7)

(8)

(9)

3 灵敏度优化分析

3.1 不同工况下各参数影响特性

首先，在建立整车动力学模型时将其底盘前、后减震器弹簧的刚度、阻尼器的压缩和复原阻尼、衬套的轴向和径向刚度、稳定杆的扭转刚度等23个参数进行参数化设置，基于整车的约束条件，确定每个变量的优化范围。为明确各参数对平顺性的影响特性，这里采用RMS-SUM、RMQ-SUM、RFG-SUM 3个评价指标进行衡量。

通过仿真分析结果，分别得出对两种工况影响“最灵敏”参数如下。

1)低频平顺性：前悬刚度和阻尼、稳定杆刚度、后纵臂与车身连接处衬套刚度、后纵臂与后桥连接处衬套刚度，后悬刚度和阻尼影响。

2)高频平顺性：前悬刚度和阻尼、稳定杆刚度、后悬刚度和阻尼影响。

通过分析整理各项指标参数可以得出如下结论：

1)后悬弹簧刚度、衬套刚度、结构橡胶刚度3个参数的影响特性一致。

2)前/后减震器阻尼参数对两种工况的影响特性为矛盾关系。

3.2 灵敏度优化分析结果

车身原状态PSD曲线和车身优化状态PSD曲线分别如图4、图5所示。图中虚线代表车身x向，实线代表车身y向。

图4 车身原状态PSD曲线

图5 车身优化状态PSD曲线

将各点位PSD曲线进行数据处理，得到两个工况下平顺性分析指标参数，见表3。表3中“-”表示在原状态基础上降低。通过与原状态进行对比分析，优化方案在保证高频平顺性工况的舒适性前提下，低频平顺性工况舒适性提升11%，优化方案效果明显。

表3 优化分析结果 %

4 结论

以电动车为原型，利用动力学分析软件Virtual.Lab 软件的Motion模块建立了刚柔耦合整车模型。通过在低频平顺性和高频平顺性两种工况上进行平顺性分析与优化，得出如下结论:

1)在进行车辆动力学仿真前需对整车模型进行校核，可以通过偏频试验和前后轮胎载荷方法，仿真与整车模型误差在8%以内，动力学模型准确，可以进行平顺性分析。

2)为保证平顺性性能的准确评判，考虑实际路面激励，建立低频平顺性和高频平顺性两种平顺性评价工况，确定每个工况下的评价指标和10个评价点。

3)平顺性优化分析中前/后减震器阻尼参数对两种工况的影响会表现矛盾的情况，故而需要明确该车的实际使用工况，明确优化分析目标。

4)为明确平顺性优化方向，对底盘参数进行灵敏度分析，确定每个参数的影响程度，明确优化对象，为整车的正向开发提供相关理论基础。