深挖方膨胀土渠道边坡变形特征分析与预测

胡 江，张吉康，余梦雪，马福恒，肖文素

(1.南京水利科学研究院，江苏 南京 210029；2.南水北调中线干线工程建设管理局，北京 100038)

我国膨胀土分布广泛，膨胀土边坡滑坡具有渐进性、季节性、滞后性和反复性等特征[1-3]。多个灌区、调水工程的膨胀土渠道运行期遭遇了滑坡问题，如淠史杭灌区运行前30 年干渠发生滑坡195 处，引丹灌区干渠运行期挖方渠段坍塌55 处，驷马山分洪道深切岭边坡运行后出现11 处滑坡，那板水库北干渠、新疆引额济克工程总干渠等也都出现过多处滑坡[1]。运行期失稳或滑坡不仅影响渠道正常运行，还会造成严重的社会、经济和环境影响，甚至威胁生命安全。当前我国正处于灌区、调水工程的大规模建设时期，膨胀土地区渠道的长期安全稳定问题备受关注，开展膨胀土渠道边坡变形特性分析和预测研究意义重大。

膨胀土滑坡一般有以下特征：多为牵引式或渐进式滑坡；多发生在持续降雨情况下；多属浅层滑动。针对膨胀土渠坡滑坡特征与演化机制，包承纲等[4-7]通过地质勘察、现场和室内试验、数值分析等手段开展了大量研究，得出膨胀土渠坡失稳分浅层破坏和深层整体失稳，浅层破坏主要为受水增湿条件下的浅表蠕变；深层破坏是受重力作用下沿内部裂隙结构面的滑动。陆定杰等[8-9]在膨胀土渠道滑坡破坏机理的基础上，提出了改性换填、防护、压重和柔性支护等滑坡破坏防治措施。

膨胀土渠道滑坡破坏具有明显的时效性，一些渠道在稳定运行较长时间后仍发生了滑坡；同时，渠坡滑坡破坏还有渐进性和滞后性[10-11]。基于安全监测数据的监控模型可定量分析边坡变形特征并进行变形预测预报，从而可及时采取合理措施进行治理。边坡变形预测研究已取得较多成果[12-13]，主要有经验公式法和统计学方法等，如斋藤法、Verhulst 生物增长模型等。谢向荣等[14]总结了膨胀土渠坡的监测项目应包含变形、应力、环境量、土体含水量、吸力、渗透压力等。膨胀土渠坡变形受地下水位、降雨、温度等环境因素和时效影响显著，依据环境量和变形监测数据，建立多因素影响下渠坡变形的数学模型，可体现各影响因素对边坡变形的影响[15-16]。

然而，目前对运行期膨胀土渠坡变形特征及应急处理研究较多偏理论方面，结合工程实践的较少。考虑到膨胀土渠道滑坡具有长期性和反复性特点，研究加固后渠坡变形特征并进行变形预测，对类似工程问题具有指导意义。某长距离调水工程一膨胀土渠段虽采取表层换填措施，但在通水运行两年后仍发生了较大变形，采取了布设伞形锚和增设排水孔等加固处理措施。为此，以该膨胀土渠段为例，基于加固处理后3 个完整干湿循环周期的安全监测数据，利用主成分聚类分析方法，分析渠坡变形的空间特征；选取典型测点，分析测点随深度、时间的变化特征；并应用时间序列分析和回归模型进行变形预测，为类似工程提供借鉴。

1 工程概况和监测布置

该长距离调水工程膨胀土（岩）段累计长约387 km，分布地域广，大气及土体干湿变化大，渠坡稳定性控制困难，运行期存在边坡稳定问题。桩号X+740～X+860 为中膨胀土渠段，左岸渠坡挖深34～39 m，渠道底宽13.5 m；过水断面坡比1∶3.0；一级马道宽5 m，以上每6 m 设一级马道，一级至四级马道间比为1∶2.5，四级马道以上坡比为1∶3.0。渠道全断面换填水泥改性土，其中过水断面换填厚1.5 m，一级马道以上换填厚1.0 m（图1）。

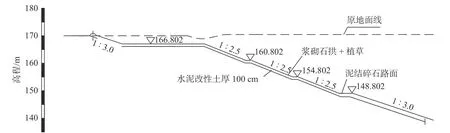
图1 渠坡断面结构示意Fig.1 Structural diagram of the canal slope

该段一级马道以上未发现大裂隙及裂隙密集带，故在渠道过水断面设置了方桩，一级马道以上渠坡未设抗滑桩。2016 年4 月，二级马道坡肩排水沟内侧沟壁倾斜变形；三级渠坡横向排水沟局部沉陷、断裂，三、四级渠坡中上部混凝土拱圈出现连续性裂缝，裂缝宽度进一步扩大，变形有继续发展趋势，表现出浅层滑移特征。渠坡变形和裂缝分布见图2。

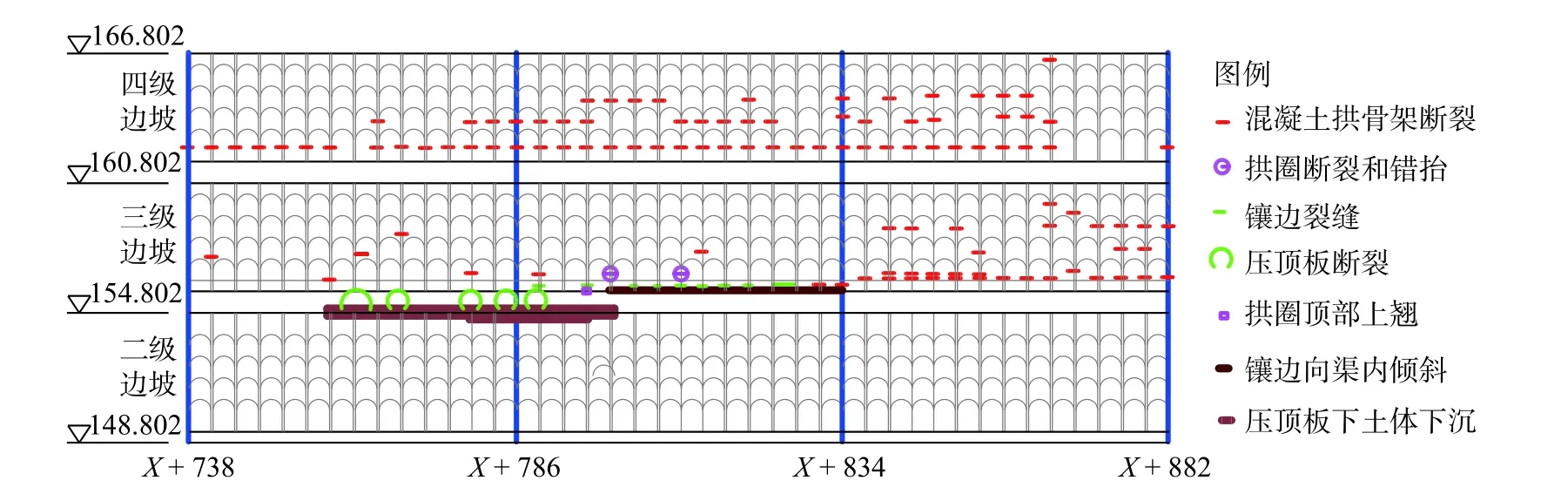
图2 三四级渠坡变形和裂缝分布（单位：m）Fig.2 Deformation characteristic and crack distribution of the third and the fourth canal slopes (unit:m)

探坑表明：X+800 四级渠坡、X+840 三级渠坡坡脚渗水，外界水体已透过渠坡局部水泥改性土换填层。查勘结果表明：渠坡在154 m 高程附近存在一深度2～8 m 的变形体。变形体产生原因为：换填层未完全隔绝膨胀土与外界水体交换，膨胀土反复胀缩、短小裂隙贯通，渠坡产生蠕动变形。

为确保工程运行安全，2016 年12 月，采取了伞型锚杆加固、排水管增设、安全监测设施安装等应急处理措施[17]。在三级渠坡沿纵向间距3 m、呈矩形布置3 排伞形锚，设计、锁定锚固力分别为100 kN 和不小于50 kN。安全监测设施主要包括测斜管、渗压计等，测斜管埋深21.5～31.5 m，测斜管和渗压计布设见图3。以805-3、805-3-m 两个测点为例说明测点的表示含义，805-3 表示桩号805 断面上3 级马道上的测点，805-3-m 表示桩号805 断面上3 级边坡上的测点。

图3 安全监测设施平面布置（单位：m）Fig.3 Layout of safety monitoring equipment (unit:m)

至2017 年4 月的监测资料表明，应急处理措施有一定效果，但变形未完全收敛。为此，2017 年6 月，在三级渠坡新增6 排伞形锚，垂直、顺水流方向间距分别为2.0 和3.4 m，设计、锁定锚固力分别为120 kN 和不小于100 kN，与前期伞型锚间隔布置。基于加固处理后、重新取基准值的变形监测数据开展分析研究。

2 基于主成分聚类分析的渠坡变形特征分析

2.1 基于主成分的聚类分析方法

主成分分析（principal component analysis，PCA）和分层聚类（hierarchical clustering，HC）都是变量相似性度量工具。当均采用Euclidean 距离时，在PCA 基础上实施HC（即HCPC 方法）可更好地描述变量间关系[18-19]。PCA 采用K-means 算法，HC 分组数使用基于Huygens 定理的Ward 标准。Huygens 定理允许分解组间、组内方差，Ward 准则使聚合两组时每步中总方差增长最小。当Q−1～Q组方差增加远大于Q～Q+1 组方差增加时，建议划分为Q组。

2.2 基于HCPC 方法的渠坡变形特征分析

采用HCPC 方法对变形测点进行聚类分析。选取二次应急处理后即2017 年7 月31 日至2020 年6 月30 日数据进行分析。图3 中测斜管最大变形及降雨量、地下水位（渗透压力）、渠道水位等环境量过程线分别见图4～5，测斜管最大变形处深度一般为0.5～2.0 m。测斜管、地下水位的观测频率为每月4 次，二次应急处理到2017 年10 月31 日基本每天1 次。降雨量为日降雨量，仅收集到2019 年的数据，渠道水位为日平均值，地下水位为805-3 渗压计测值。

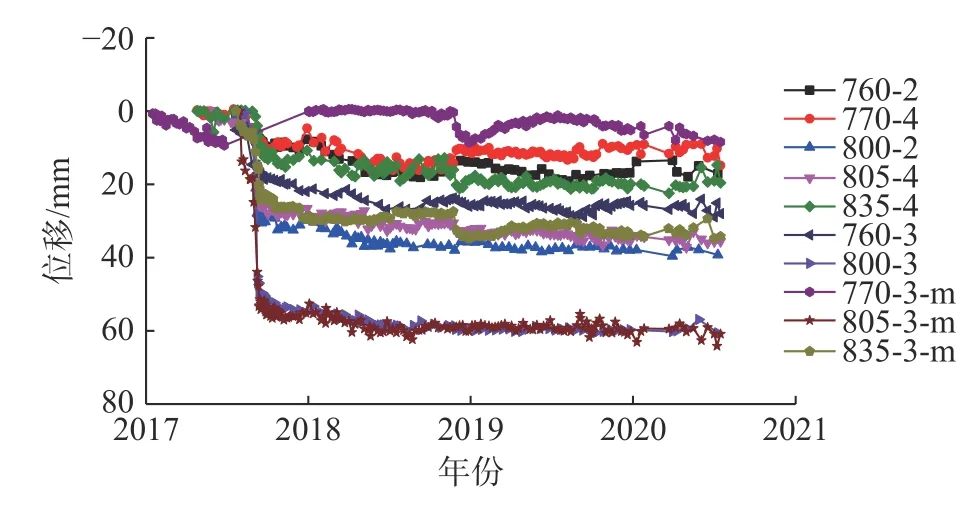
图4 各测斜管表面测点位移过程线Fig.4 Displacement records of surface measuring points of the installed inclinometer tubes

图5 渠段环境量过程线Fig.5 Records of environmental quantities in the canal slope

二次应急处理后，已完整地观察了在3 个干湿循环周期。总体看，加固处理后渠坡变形有以下特点：向渠道内变形量逐渐增大；二级与四级马道间变形同时发生，具有相似变形过程和良好同步响应性；各处变形量并不相同，具有较明显不均一性，在干湿循环条件下，二级与三级边坡间变形量最大；渠坡经历了从变形到逐步稳定的过程，伞型锚锚固力调整2 个月左右，相应地，渠坡经历了加速变形到稳定发展的阶段，2017 年11 月后，群锚效果开始显现，变形趋于稳定，但存在一定的周期性波动。

采用HCPC 法对各测斜管最大位移点变形进行分析，得到树状分区结果见图6，建议的最优分区数Q为3，映射到渠坡如图7。位移空间分布具有明显不均衡性，X+805、X+835 三级渠坡变形最大，形成了一个单独的分区。变形向两侧减弱，且X+760～X+800 区域变形相对较小，也形成了一个单独的分区。结合险情处置探坑和查勘结果，X+805 附近三级渠坡在154 m 高程附近存在一滑动面，可知上述变形特征是膨胀土渠坡滑移带造成的。为此，后文中选取835 断面上三级渠坡上805-3-m 测点进行重点分析和预测预报。

图6 变形测点树状分区Fig.6 Dendrogram of the deformation measuring points

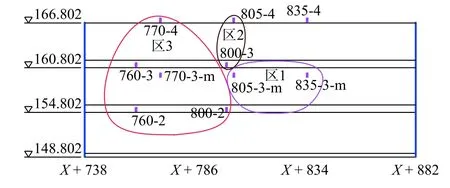
图7 变形测点分区平面映射(单位:m)Fig.7 Plane mapping of clustering zones of the deformation measuring points (unit:m)

805-3-m 测点典型时刻沿深度方向的位移分布见图8。可见，同一支测斜管孔口部位位移变化相对较大，5～7 m 深处存在一个变形急剧加大区域，之上为变形体；之下渠坡变形量逐渐减小；渠坡采用水泥改性土换填未完全隔绝膨胀土与地下水位、大气水交换。

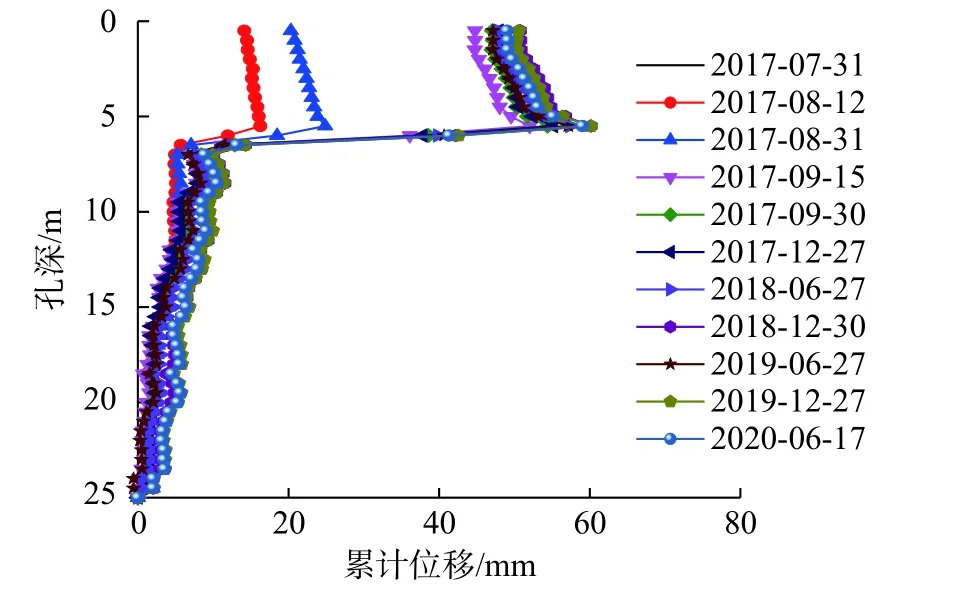
图8 805-3-m 测点沿深度方向的位移典型时间过程线Fig.8 Typical time history of displacements along depth direction of 805-3-m

3 渠坡变形的主要影响因素分析

渠坡变形是内外因综合作用的结果，地质构造、土体物理力学性质等内因主导了变形，降雨、地下水、蒸发、温度和时效等外因加速了变形。

3.1 胀缩因子

膨胀土具有裂隙性及吸水膨胀、失水收缩等特性。降雨、蒸发、温度、地下水会引起膨胀土土体含水率变化，导致膨胀土渠道胀缩，统称为胀缩因子[20]。干湿循环（降雨与蒸发交替）是引起土体含水率变化的主因，降雨决定土体湿化程度及入渗深度，是渠坡变形的最直接气候因素，该调水工程施工期约80%的滑坡由降雨触发[2]。蒸发引起土体裂隙。已有试验结果[11]表明，每次干湿循环，膨胀土边坡均累积了向坡下的沉降和水平位移。

降雨入渗有一定滞后性，且由于地表径流、水分蒸发等原因，入渗量要小于降雨量。用于渠坡变形分析的降雨量一般取当天及前几天的降雨量记录。进入岩土体降雨量的经验式：

式中：r为有效降雨量；a为有效雨量系数，一般取0.84；n为前第n天，一般为15 d。

大气蒸发、气温变化会引起土体温度变化，进一步引起含水率变化，从而导致膨胀土渠坡变形。根据经验，可取单位时间的平均蒸发量、气温作为影响因子。

地下水是影响渠坡变形的另一重要因素，地下水不仅可加快结构面软化，使得滑面抗滑力降低；还能在底滑面上提供扬压力、在后缘拉裂面提供静水压力，导致渠坡变形和滑坡启动。在初始蠕变、稳定变形及加速蠕变阶段，地下水均会产生很大影响。渠道水位、地下水位因子则参考文献[21]，取1～3 次方。除降雨外，该调水工程施工期剩余的滑坡明显受到地下水影响。根据图5 可知，渠段的地下水位略高于渠道水位，主要受外界和降雨影响。

3.2 时效因子

膨胀土渠坡时效变形原因复杂。一般地，边坡变形的时效[22]可表示为：

式中：θ为观测日至始测日累计天数t除以100；c1，c2为时效因子系数。

渠坡运行期受干湿循环周期性变化，还应当考虑周期性因子的影响：

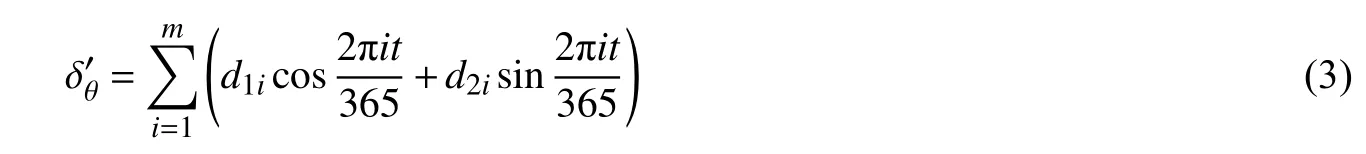
式中：d1i、d2i为周期因子系数；m一般取1～2。

3.3 渠坡变形与环境和时效的相关性

对805-3-m 测点2018—2019 年的表面最大位移与平均气温、有效降雨量、渠道水位、地下水位、时效等进行相关性分析，Pearson 相关系数见表1。由表1 可知，表面位移与时效、平均气温相关性最大，相关性在0.4～0.6 范围内，为中等程度相关；其次为地下水位，相关性在0.2～0.4 范围内，为弱相关；与渠道水位相关性小于0.2，为极弱相关；同时，与有效降雨量呈中等程度负相关。

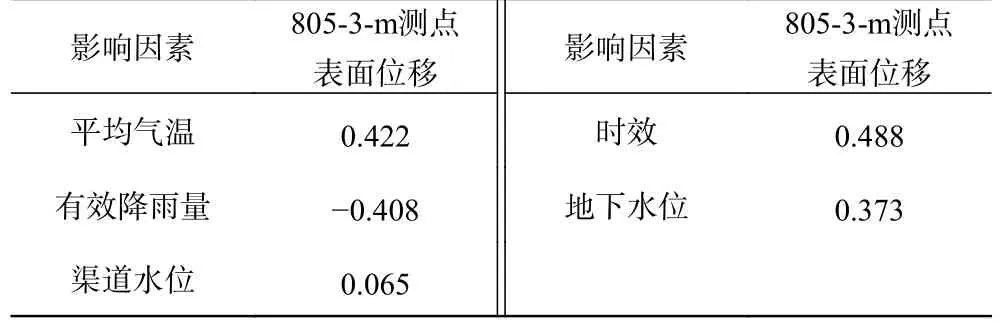
表1 805-3-m 测点表面位移与影响因子间相关性Tab.1 Correlation coefficients between 805-3-m and influencing factors

4 变形预测预报模型

4.1 指数平滑法分析

时间序列模型常用加法模型：

式中：Tt为趋势项；St为波动项（季节和周期项）；Rt为随机或偶然项。

局部加权回归指数平滑法[23]以当前时刻为起点，利用历史信息预测未来变化，较近时间数据影响较大，更切合实际，且能消除随机干扰的影响进行时间序列分析。加权系数对预测精度有较大影响，系数越大，加权后序列衰减越快，系数宜取0.1～0.3。经试算后，取值0.2 时效果最好。

浅表层土体活动明显，以2017 年7 月31 日至2019 年12 月31 日间805-3-m 测点表面最大位移为例判断变形的发展和趋势。实测值与分离后的趋势项、周期项见图9。从图9 可看出，伞型锚实施加固后前期渠坡变形速率快，后期随锚固力增大渠坡变形速率趋缓。

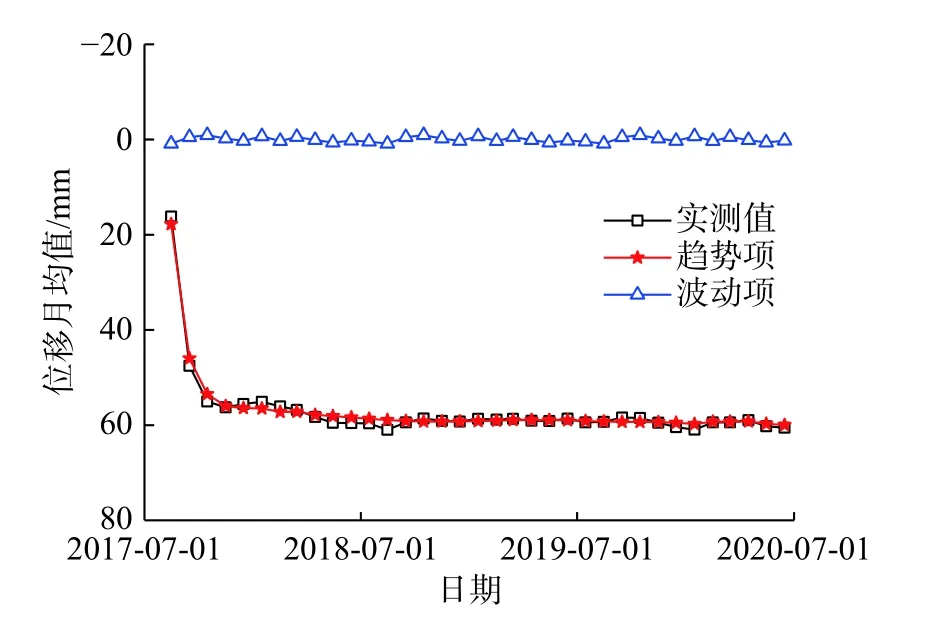
图9 指数平滑法分离得到的趋势项和波动项Fig.9 Trend and fluctuation terms separated by the exponential smoothing method

4.2 自回归移动平均模型预测

差分自回归移动平均模型（autoregressive integrated moving average model，ARIMA）[23]也是根据过去数据预测未来数据，AR 为自回归模型，MA 是移动平均模型，ARIMA（p，d，q）模型为：

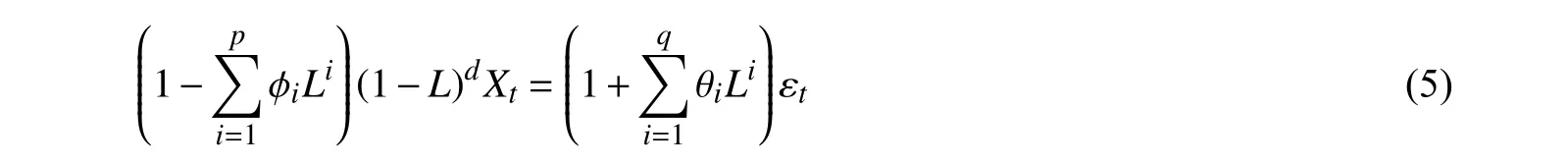
式中：d为使序列平稳的差分次数即阶数，d∈Z（Z为整数），d>0，一般不超过2；L为滞后算子；εt为白噪声序列；φi（i=1，2，···，p）为自回归模型系数，p为自回归项；θi（i=1，2，···，q）为移动模型的系数，q为移动平均项数；Xt为t时刻的随机变量值。

采用ARIMA 模型预测的时间序列须是平稳的，对非平稳时间序列需进行平稳化处理。建立ARIMA模型的步骤为：分别采用自相关函数、Box-Ljung 法检验平稳性和白噪声；基于Box-Jenkins 方法进行模型识别；使用最小AIC 准则对模型定阶，确定差分和移动项数；建立模型并验证。

以2017 年7 月31 日至2019 年12 月31 日期间805-3-m 测点表面最大位移时间序列为例建立ARIMA 模型，采用10 阶交叉检验验证模型可靠性，并以最后半月数据检验模型预测精度。通过2 次差分序列变为平稳，且通过白噪声检验；对模型进行定阶；建立模型ARIMA（1，2，2），残差为白噪声，且参数显著，模型同构10 阶交叉检验，以此预测变形。模型训练、预测阶段的平均绝对误差、平均绝对百分比误差分别为0.195、0.462 及0.262、0.637。模型拟合和预测值与实测值对比见图10。

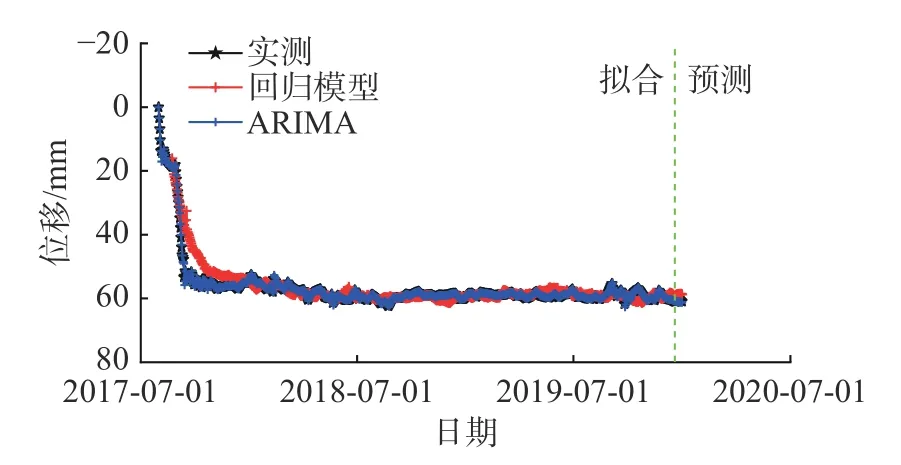
图10 ARIMA 和回归模型拟合与预测效果Fig.10 Comparison of fitting and prediction values between ARIMA and regression models

4.3 多因素非线性回归模型分析

进一步建立2017 年7 月31 日至2019 年12 月31 日期间805-3-m 测点表面最大位移时间序列的多元非线性回归模型。根据前文分析，选取了有效降雨量、地下水位、渠道水位、日均气温、时效等影响因素。模型复相关系数R2为0.908，训练、预测阶段平均绝对误差、平均绝对百分比误差分别为0.923、2.830 及1.022、3.150。模型通过了10 阶交叉验证，拟合预测精度较高、具有稳健性。拟合和预测值与实测值对比见图10，各因素对变形的相对影响见图11。可见，时效在伞形锚加固处理后为主导因素，地下水位、降雨量和温度也是主要影响因素，渠道水位影响较小，这与该调水工程渠道水位平稳、变化小有关。为此，在实测降雨量、温度、地下水位的基础上，构建渠坡变形与多因素之间的函数关系，可以建立符合膨胀土渠坡变形的经验性预测模型。

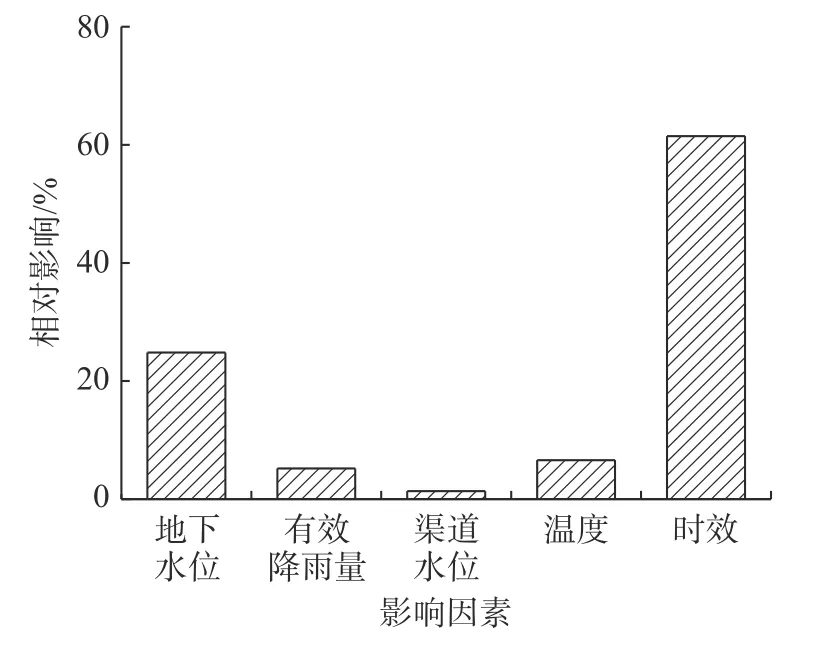
图11 各因素对变形的相对影响Fig.11 Relative influence of various factors on deformation

从以上对比分析可知，采用指数平滑法可分析膨胀土渠坡加固处理后运行初期的趋势性和周期波动性，利用ARIMA 模型、多因素非线性回归模型可预测其变形，且构建的回归模型还能分析各因素对变形的影响大小，指导运行管理。

一般地，膨胀土开挖渠坡在经历2～3 个以上干湿循环后易发生破坏。该段渠道2014 年12 月通水运行，在2016 年发生了较严重的变形。2017 年6 月二次伞形锚锚固处理后，渠坡变形经历了加速变形到稳定发展共2 个月左右的调整，之后群锚效果显现，变形趋于稳定，但受降雨、地下水位及气温等因素影响，存在一定的波动，仍应加强雨季的巡查和安全监测。

5 结语

（1）深挖方膨胀土渠道受降雨、蒸发、地下水位、气温等外界环境因素影响，渠坡变形机理复杂，若未隔断周边地下水、大气环境的影响，渠坡运行期易面临滑坡破坏风险。

（2）实施伞形锚、排水孔等加固处理措施后，深挖方膨胀土渠坡变形经过短暂调整后，变形趋于平衡，采用伞形锚处理效果较好。

（3）巡视检查和安全监测能及时发现深挖方膨胀土渠坡变形和破坏迹象。采用指数平滑法可分析其变形规律，利用ARIMA 模型、回归模型可预测其变形，分析各因素对变形的影响，从而指导运行管理。

（4）深挖方膨胀土渠坡变形破坏具有长期性、反复性及空间不均衡性等特点，应基于已积累的大量监测数据，采用大数据挖掘技术，在时空两方面对渠坡稳定进行分析和预测，以进一步提高膨胀土渠坡变形安全监控的有效性。