窝崩治理新型结构—布帘石的理论分析和试验研究

应 强，张幸农，假冬冬，陈长英

(南京水利科学研究院 港口航道泥沙工程交通部重点实验室，江苏 南京 210029)

窝崩具有很强的突发性，而且土体崩塌发展速度快、范围大，通常1～2 d 时间内就会形成横宽、纵深达数十甚至数百米的巨大窝塘，崩塌土体可达上百万立方米，对防洪、河势和地方经济及社会发展的危害极大[1-3]。在窝崩险情的应急治理方面，江苏省目前已形成了“守两肩、固周边、先促淤、后封口”的险情抢护及后续治理原则，抢护材料大多选用树头石[4]、抛石、四面六边体混凝土框架[3,5]及塑枕坝等，实践证明，树头石促淤效果很好，但由于树头石需砍伐大量的树木，会对生态产生一定的影响。

借助柔性导流坝[6-7]概念，在窝塘防冲促淤中，提出了一种以宽度较小布匹为载体，顶部连接浮块（浮块的浮力为T0），底部袋装石块的结构[8-9]，仿照已有的树头+石块为树头石的命名，称此结构为布帘石。作为新型的阻水结构，布帘石在水中的沉浮状态、力学机制及阻水效果都需进行研究。

布帘石在水流中的受力尚未有过理论探讨，有的作者认为其与锚链受力相似，符合悬链线方程[9-11]。在不考虑锚链受水流力作用，只考虑重力作用时，两者受力相似；如考虑水流力和重力综合作用后，悬链段水平投影长度和锚链力均较经典悬链线方程的计算结果要大，且流速越大，偏差越大[12]。布帘石也同样受水流力和重力综合作用，但布帘的自重较小，受水流力的作用较大，因此其剖面形态与悬链线的偏差应更大，故需进行研究。

1 方程推导

布帘石在水流中的状态如图1 所示。设布帘石宽度为bB，长度为L，浮力为T0，布置在水深为H、垂线平均流速为V的水流中。在水流作用下，布帘石阻水高度为Hs，水平投影长度为bL，任取布帘石部分长度为∆L的微元，其受力情况（见图2）为：①两端张力T和T+∆L,其作用线与x轴成θ角；②水流水平推力f(y)∆y；③水流上举力f(x)∆x；④水中自重为σg∆L，σ为布帘的线密度，g为重力加速度。

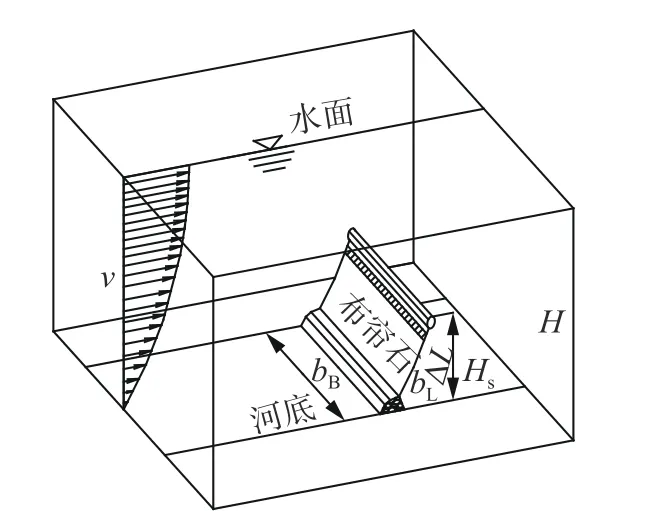
图1 布帘石在水流中的状态Fig.1 Condition of curtain-stones in flow

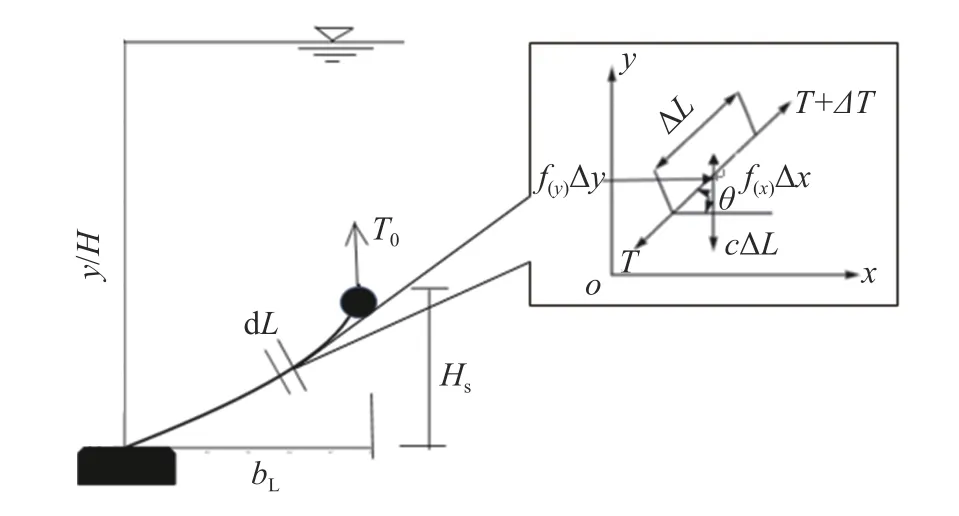
图2 布帘石在水流中临界状况及受力分析Fig.2 Stress analysis of curtain-stones in flow

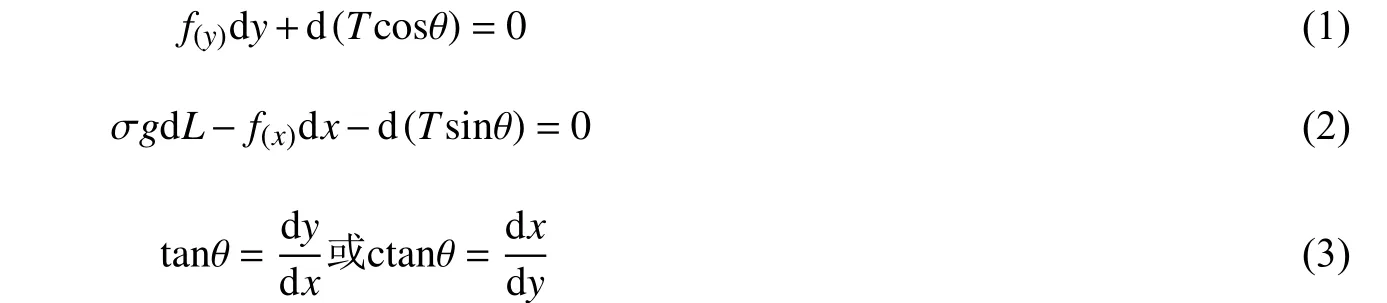
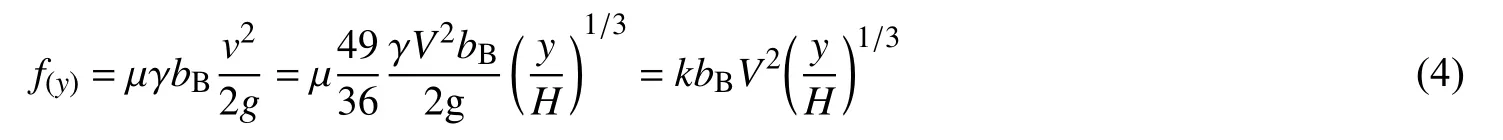
式中：V为垂线平均流速；k，µ为水平推力系数，γ为水的重度；上举力f(x)与布帘在水中的重力 σg为方向相反的两个力，且两者均不大，可认为σgdL−f(x)dx项忽略不计，即由式（2）可得d(Tsinθ)=0。这样式（1）可变为：

对式（5）进行积分，并认为在布帘顶端仅有浮力的作用，即有y=Hs，x′=0，由此确定积分常数。

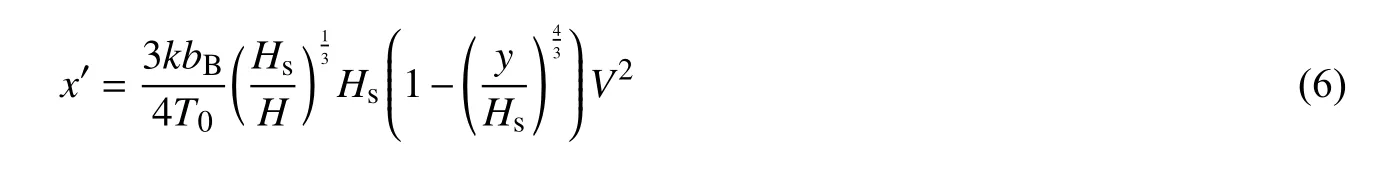
求解式（6），可得：

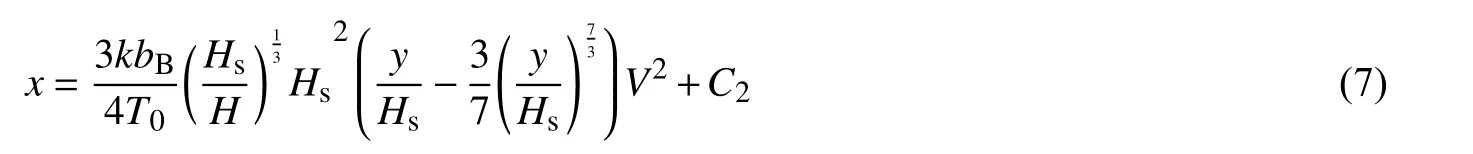
由y=0，x=0可得C2=0：则剖面曲线方程为

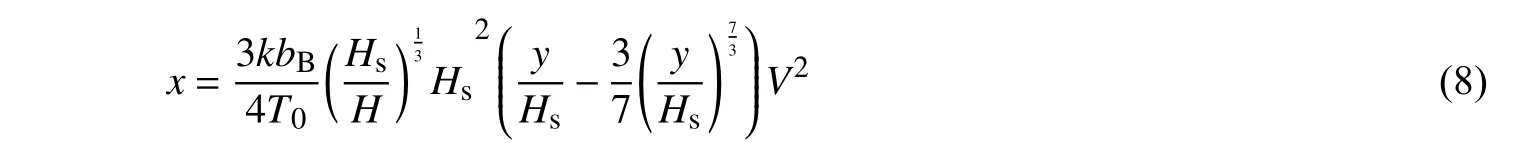
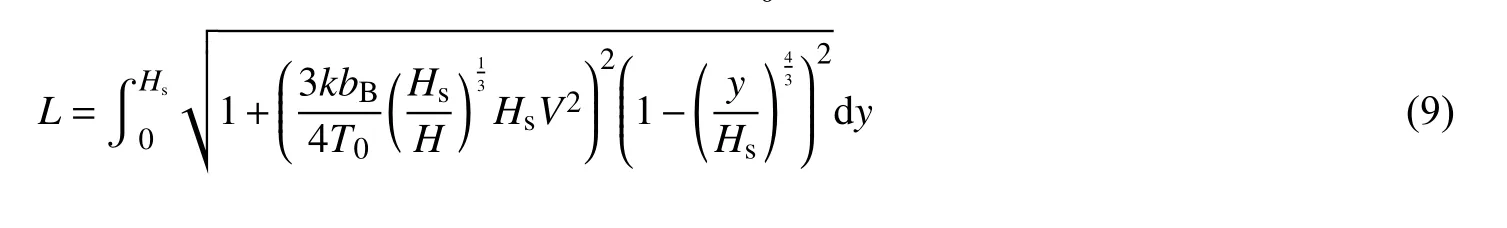
2 系数确定

由式（4）可见，系数k与水流水平推力系数有关，文献[9]进行了布帘石处于水面临界状态（即Hs刚好等于H0）时，浮力T0、流速V0、水平投影长度bL0间的水槽试验，试验采用的水深为20～40 cm，流速为22～55 cm/s。

当Hs=H0时，式（8）可改写为：

研究区域位于辽宁省鞍山市千山山脉西北脚下，全国较为典型的深凹露天铁矿，已有百年的开采历史。2017年6月，按照矿山和选矿厂位置，依地形围绕矿区在毗邻城区方向5 km2范围内，设置11个样点，分别标记为S1～S11，具体布点如图1。采用五点取样法采样，每个样点均采集0～20 cm表层土壤，去除土壤中动植物残体、石子等杂物，充分混匀后取1 kg左右装入自封袋，编号，密封带回实验室后风干，用四分法选取土样并经粉碎研磨，过100目筛备用。

当y=H0时，x为布帘石的水平投影长度bL0，可得：

图3 计算和实测的b L值比较Fig.3 Comparisons of calculated and measured bL values

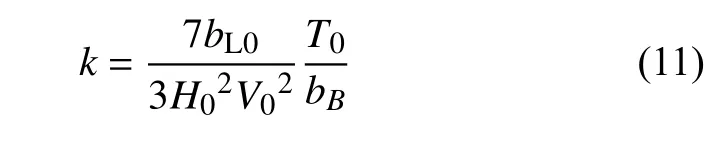
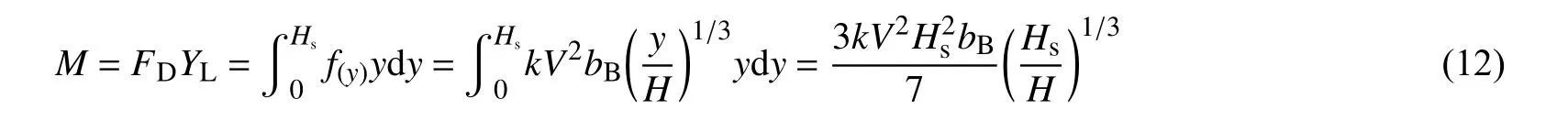
说明式（8）的物理意义是以布帘石与河床底部接触处为中心，上浮力力矩与水流对布帘作用力的力矩平衡。

3 方程验证

试验在宽4 m、高50 cm 的水泥光面底的水槽中进行，试验水深为30 cm，摆放布帘石处的垂线流速分布见图4，垂线平均流速为5.4 cm/s。采用的布帘长度L=16 cm，宽度bB=10 cm，底端由3 根10 cm 长的4#铁丝压重，顶端由为0.5 cm×0.5 cm×10.0 cm 的泡沫塑料条作浮块，其浮力为0.070 N。由式（8）计算和试验测量的剖面方程曲线见图5。可见，水槽流速分布与对数分布较为符合，但计算布帘剖面与实测剖面有所差别，这可能与公式推导中忽略了布帘的自重有关，当布帘自重与浮块自重占比增大时，其偏离值也会增大。

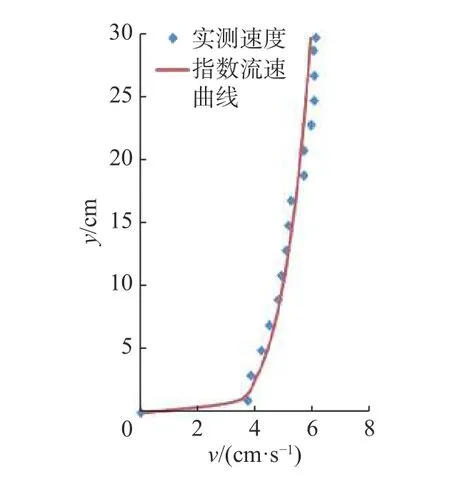
图4 垂线流速分布Fig.4 Vertical velocity distribution

图5 布帘石剖面计算和实测剖面比较Fig.5 Comparison between calculated and measured sections of curtain-stone

4 布帘石在水中状态的讨论

置于河流中的布帘石，浮块在水中会出现浮于水面、没入水中两种状态；布帘也有全部浮于水中和部分（近底段）沉入河底两种状态；假设设计时河流中水深为H0、流速为V0、浮力为T0时，浮块顶刚好处于水面和没入水中的临界状态，由式（8）可以得出剖面方程，由式（9）可以计算出布帘长度L0，此时，水流力矩与浮力矩处于水面临界平衡状态，由式（11）改写为：

4.1 浮块顶浮于水面或没入水中的状态分析

当流速V、水深H有一个变小，或两者都变小时，由于作用于布帘上水流力矩减小，浮块的浮力矩不变，浮力矩大于水流力矩，促使浮块上浮，直到浮块部分浮出水面后，浮力减小到T，当等式成立后达到新的平衡。

当流速V、水深H有一个变大，或两者都变大时，此时水流力矩已大于浮块的浮力矩，于是水流将布帘没于水中，以减小布帘所受的水流力和力矩，同时增大bL值和浮力矩，直至达到形成新的力矩=1平衡。图6 为流速V增大后的布帘剖面状态。

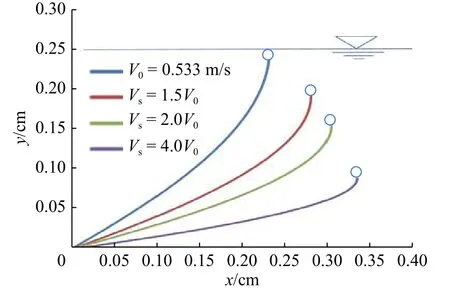
图6 流速增大时布帘剖面情况比较Fig.6 Comparisons of profiles with increasing velocity

4.2 布帘浮于水中或沉入河底的状态分析

当实际采用的布料长度L大于临界状态的布料长度L0时，由于流速、水深、浮力等因素不变，由式（10）可知，其剖面形式也不会改变，多余的长度L−L0会沉在河底。文献[7]中临界状态时L0=1.2H0，并给出了同样为临界条件时，当布帘长分别为L=1.5H0和L=1.8H0时由试验所得的沉底布料长度，其试验所得的沉底布料长度与L−L0值基本相同。图5中还绘制了水深、流速与验证时相同，但浮力减小一半后的布帘石剖面情况，可见，这种情况下，有3.5 cm长的布料沉入河底。

5 布帘石阻水效果研究

布帘石阻水效果试验在南京水利科学研究院1∶100 的正态局部模型中进行，模型模拟2017 年11 月8 日在长江扬中市指南村附近发生窝崩后的窝塘地形及附近长江河床地形（见图7（a）），模型模拟的原型流量为28 500 m3/s，模型制作、口门流速、水位的验证见文献[13]，在验证相似后，进行了4 种方案试验：①窝塘内无工程；②窝塘内布置布帘石（高7 m、宽2 m、6 m×6 m 的间距，每条布帘重647 N，浮力3 038 N，下端固定在河床上（见图8（a））；③高7 m、6 m×6 m 的间距布置树头石；④高5 m、6 m×6 m 的间距布置树头石（见图8（b）），窝塘内共布置了12 个测点，各测点的位置见图7（b），测量了各方案窝内各测点流速流向值，窝塘内布置布帘石后窝塘及其附近长江河道内的表面流速分布见图9（a），窝塘内12 个点0.2H、0.6H和0.8H处的流速流向分布见图9（b），无工程方案（方案①）及2 种高度的树头石方案（方案③、方案④）的试验成果可参考文献[13]，作为总体效果比较，采用数学平(均的方法)统计了各方案窝内各点的平均值，计算V无−V方案i/V无值作为各方案减速效果。计算表明：布帘石方案减速效果为14.2%，5 m 和7 m 高树头石分别为：11.8%和16.1%。可见，布帘石方案与同高度的树头石方案阻水效果相当。

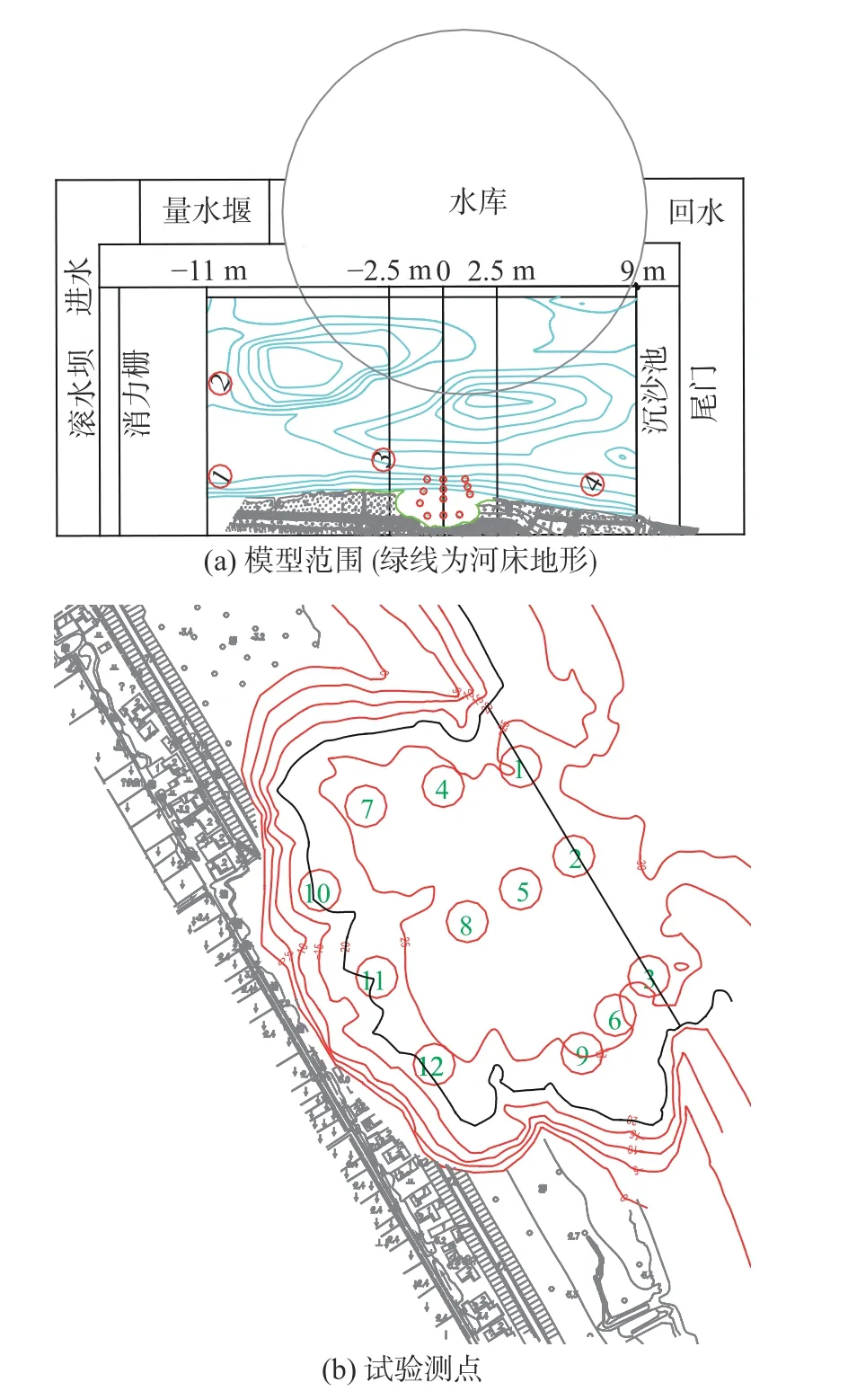
图7 模型范围及试验测点示意Fig.7 Scope of physical model and test points

图8 布帘石与树头石布置Fig.8 Layout of curtain-stone and tree head-stone

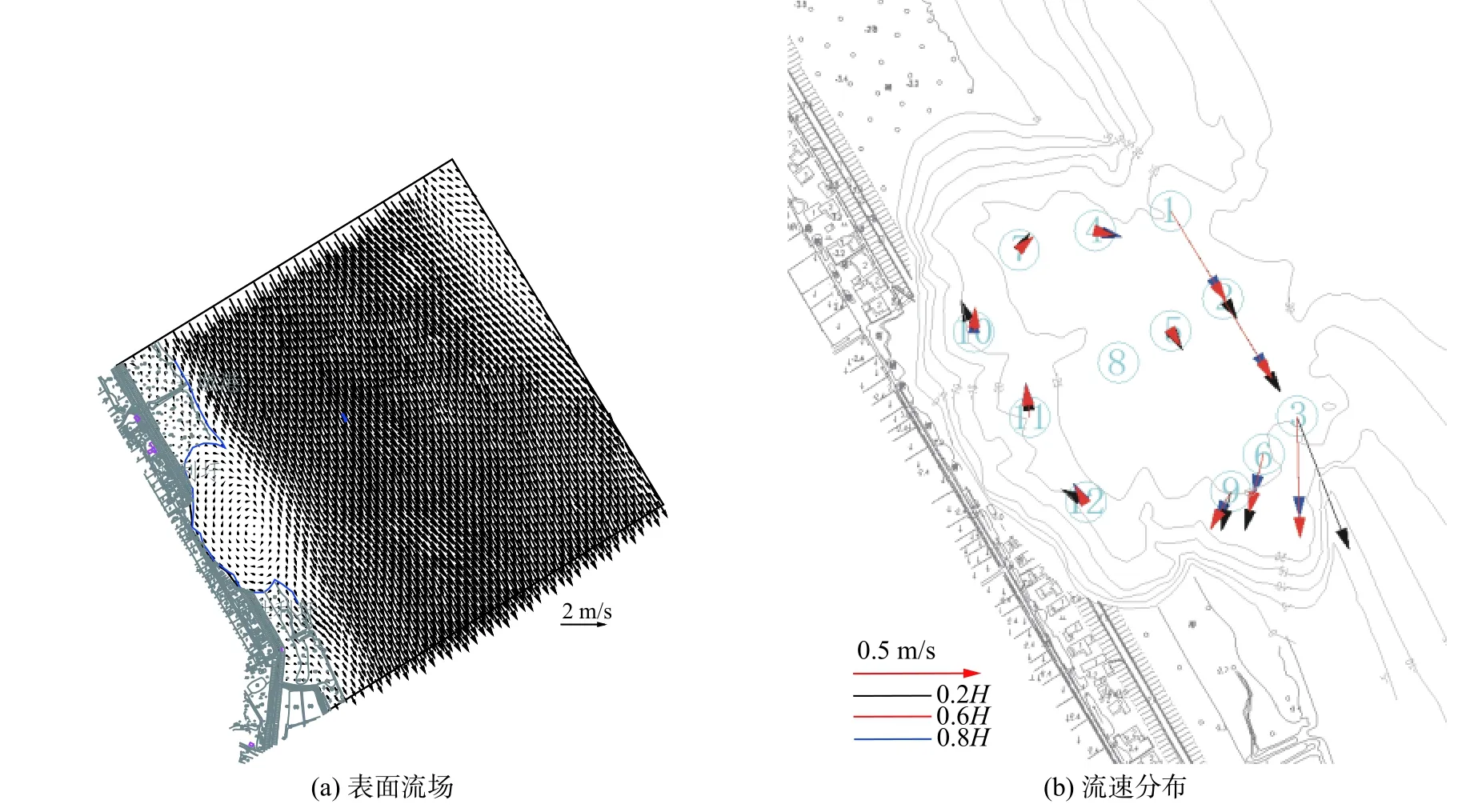
图9 布帘石布置的表面流场及流速分布Fig.9 Surface flow field and velocity distribution after layout of curtain-stone

6 结语

（1）分析了布帘石在水流中的受力状态，推导了布帘石在水流作用下沿水深方向分布曲线（面）方程，并根据试验资料确定了方程中的系数。方程的物理意义是以布帘石与河床接触点为中心，浮块的上浮力力矩与水流对布帘作用力的力矩相平衡。

（2）探讨了布帘石在水流中可能出现的各种状态的机理，可得流速、水深、布帘长、浮力间存在一种平衡（临界）关系，当流速、水深大（小）于临界状态时，浮块会没入（浮于）水中；当布帘长度大于临界状态时，超过部分会沉于河底。

（3）正态局部模型试验表明，布帘石的阻水效果与相同布置方式下树头石的阻水效果相当，可用作窝塘内的促淤结构。