离心泵径向力的数值模拟与实验研究

朱艾晨，高翼飞，李国栋，边 玉(沈阳工业大学 机械工程学院，辽宁 沈阳 110000)

0 引言

泵作为全球使用最广泛、种类最多的通用机械之一，设计时要综合考虑其运行的可靠性、水力性能、工作效率等技术指标，而水泵径向力的大小是影响泵组运行可靠的重要因素[1]。径向力能够让泵轴受到交变应力的作用，产生定向的挠度，其大小直接影响泵工作的稳定性。此外，径向力也会增加轴封之间的间隙，而不均匀的间隙也是离心泵发生泄漏的主要原因之一[2]，如果不能够很好地平衡泵轴受到的径向力，导致叶轮与机壳摩擦变大、负载增大、产生振动以及噪声[3-4]。若设计不当，会导致水泵无法正常运行，产生故障。因此，研究泵的径向力具有重要的意义。

目前研究径向力的方法主要有三种，包括经验公式法、测试法以及数值模拟预测法[5]。

大多数采用的经验公式都是关醒凡[6]在书中所提到的计算公式，经验公式见式(1)：

F=9.81KtHD2B2×103

(1)

式中：H—泵扬程 (m)；D2—叶轮外径 (m)；B2—叶轮出口宽度 (m)；Kt—实验系数，可按下式计算：

(2)

测试法又分为直接测试法和间接测试法。直接测试法就是通过测量泵轴上的应变来确定离心泵的径向力，考虑到轴套以及支撑点的原因，测量径向力需要设计专用的测量设备，因此成本较高。文献[7]通过应变片以及专门的测量装置测出大型双吸离心泵泵轴所受的弯应力进而测定叶轮所受径向力的大小。间接测试法就是将应变片或压力传感器安装在离心泵滚动轴承的合适位置。经过计算机数据处理，得到测量结果。目前对于间接法的研究主要是确定适合安装测力传感器的位置。卓震[8]等人提出了用多点应力法来测量离心泵的径向力。为了准确测量出应力的大小，应变片的布置位置如图1所示，得到各个点上的压力，再采用线性插值的方法求得叶轮所受到的径向力大小。由于采用的线性插值方法，会导致计算结果出现一些误差[9]。

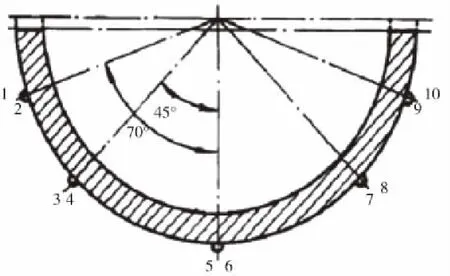
图1 应变片粘贴位置

相对于测试法的费时费力，数值模拟相对来说非常的方便，只要有正确的物理模型，就可以准确的反映出泵内部流场的流动规律[10-12]。如今，数值模拟已经成为研究人员分析实际工程中流体内部运动的重要方法之一。若将试验手段和数值模拟手段联系在一起，改善应用的数学模型，就可以使数值模拟结果与实际内部流动的情况一致。本文正是采用数值模拟和试验相结合的方式来预测并验证一种离心泵径向力大小。

1 离心泵径向力计算的数学模型

1.1 出口压力法

应用Fluent对离心泵的内部流场进行仿真，得到叶轮出口与蜗壳之间的连接面的静压分布。假定在连接面的各个网格节点附近的静压均匀分布，把每个网格节点的面积看作是相等的。这样就可以先通过求解面上每一个节点上所受到的力，通过力的分解合成定理，分别计算在y、z向受到的力，最后得到总力的大小以及方向[13]，如下所示：

(3)

(4)

(5)

(6)

R2—叶轮出口半径；

B2—叶轮出口宽度；

N—连接面网格节点的个数；

Pi—第i个网格节点的压强。

将各流量工况下数值模拟得到的连接面的静压分布根据上述公式进行计算，就可以得出叶轮在各流量工况下所受到的y、z向径向力的大小和方向，以及总径向力的大小和方向。

1.2 径向力计算的直接积分法

在CFD软件Fluent中直接积分法是很容易实现的，因为Fluent可以直接获取边界上所受到的作用力大小以及方向，所以我们可以很轻松的得到一个边界上沿着x、y、z方向上的作用力[14]。这种用Fluent进行直接积分的方法能够考虑到液体本身所具有的粘性力，因此比上节建立的模型更加准确。

2 离心泵内部流场的数值模拟

2.1 控制方程

坐标系选用固定在叶轮表面的旋转坐标系，可将叶轮内的流动看作是定常流动，整个流场内部看作是三维不可压得稳态湍流场，建立相对坐标系下的时均连续方程及N-S方程，采用RNGk-ε湍流模型封闭方程组。

2.2 边界条件

1)进口边界条件：进口条件就是指定进口边界上流动介质的参数，常用的进口参数一共有三种：进口速度、进口压力和进口质量。当介质是可压缩的情况下，一般选用进口质量作为进口边界条件；当介质是不可压缩或未压缩的情况下则选择进口速度或者压力作为进口条件。因为本次实验选择的介质是清水(water-liquid)，属于不可压缩，又因为只要改变进口速度，就可以很轻易的改变离心泵的流量，因此选择进口速度作为本次实验的进口边界条件。

2)出口边界条件：出口边界条件同样分为三种：压强出口(outlet)条件、压强远场条件以及出流(outflow)边界条件。其中压强远场条件是指在给定自由流马赫数和静参数条件确定后，给定无限远处的压强条件，因此跟本次实验的不可压缩计算不适合。压强出口条件相比于出流边界条件来说，前者在出现回流的时候更容易在迭代过程中收敛，而本次实验的出口区域远离回流区域，因此选用出流边界条件作为本次实验的出口边界条件。

3)壁面条件：在叶片表面、轮毂等固体壁面上，速度满足无滑移条件，采用标准壁面函数法对固壁附近的流动进行确定[15]。

2.3 建模及网格划分和控制方程的离散与求解

采用Pro/E三维建模软件进行本次离心泵的建模，并用ICEM-CFD软件划分网格。如图2所示。利用有限体积法计算离散控制方程，速度和压力耦合采用SIMPLE算法，实现速度与压力的耦合。连续性方程、动量方程、湍动能方程和湍动能耗散方程都采用二阶迎风格式来进行离散计算。

图2 模型建立及网格划分

3 离心泵数值模拟的结果与分析

对离心泵进行数值模拟分析，经过538次迭代后得到收敛解。图3为该离心泵在流量为0.5 m3/s下的残差图。

图3 残差收敛曲线图

经迭代，其他工况也是收敛的，因此可以分析各个流量工况下的数值模拟结果。

3.1 流量-扬程曲线

扬程(H)：指水泵能够扬水的高度。在Fluent软件里面并没有直接显示扬程的功能，但是我们知道扬程可以通过压力来计算，最常用的水泵扬程计算公式是：

(7)

其中，H—离心泵扬程(m)；P1—离心泵进口处液体的压力(Pa)；P2—离心泵出口处液体的压力(Pa)；C1—离心泵进口处液体的流速(m/s)；C2—离心泵出口处液体的流速(m/s)；Z1—离心泵进口高度(m)；Z2—离心泵出口高度(m)。

在实际计算当中，还会将流速之后的部分进行省略，省略之后的公式为：

(8)

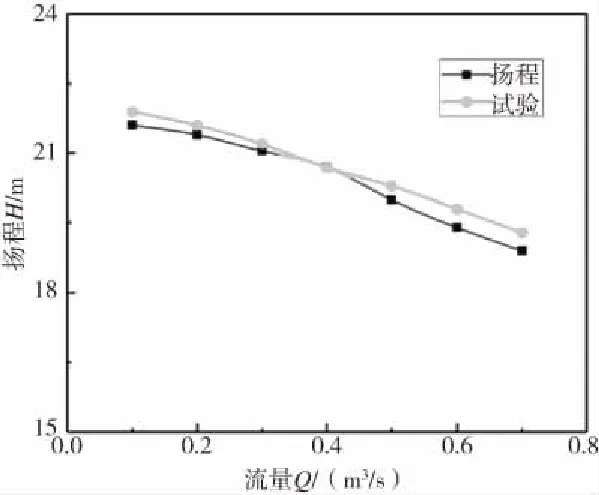
图4 流量-扬程曲线

在Fluent后处理的Report面板中找到Surface Integrals，表面选择进出口面(inlet、outlet)，就会在计算窗口处得到离心泵的进出口压力值。再根据上述计算公式求出数值模拟情况下的扬程。本实验采用的离心泵数值模拟和试验的流量扬程曲线图如图4所示，对比发现变化趋势比较一致，误差不超过8.3%。因此，采用数值模拟的方法来分析本次离心泵叶轮的径向力。

3.2 径向力数值计算

图5是在设计工况Qn=0.5 m3/s下，离心泵中间截面的静压力分布情况。利用Fluent的后处理，求出并导出不同流量工况下的静压分布。将导出的数据用EXCEL软件打开，结合第二部分所述的计算公式，算出y、z方向的径向力以及总径向力。如表1所示。

图5 离心泵中间面的压力分布

由表1可以看出，在设计流量工况下，叶轮依然会受到径向力的作用，这是因为泵体的非对称结构会使泵内部流场的流量、流速及叶轮出口的压力产生非对称分布[16]。各工况下所受到的径向力大小和方向都不一样，随着流量的增加，测得的径向力先变小后变大，其中当流量为设计流量时，叶轮所受径向力最小。

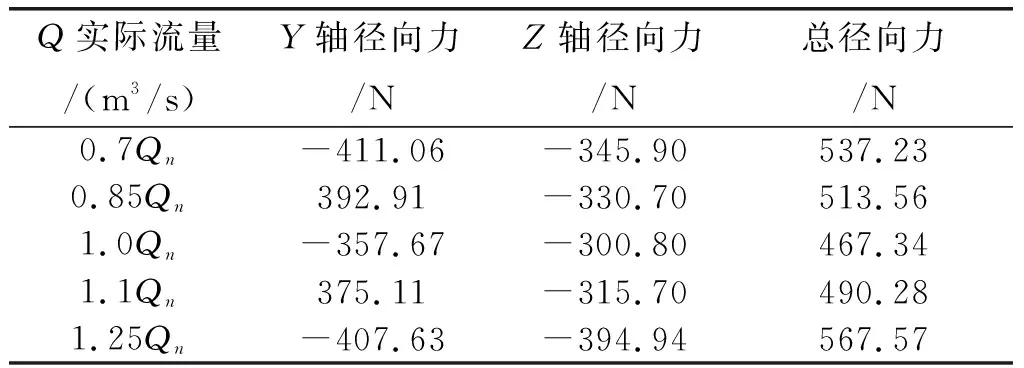
表1 不同流量下径向力数值计算

4 实验与数据分析

4.1 测量装置的设计

离心泵径向力测量装置的径向力测试原理示意图如图6所示，测力装置包括套在轴承1外的轴承座2。轴承座沿其圆周处分布3个通孔，将传感器3依次安装在通孔内。压力传感器一端抵靠于轴承的外表面，另一端通过压紧螺栓4安装于通孔内。使得离心泵转轴旋转时，离心泵转子由3个压力传感器支撑。压紧螺栓通过压盖7和螺栓6安装于轴承座上，同时还设有锁紧螺母5。轴承座上设有导线孔，用于穿过压力传感器的输出电缆，以便于连接数据采集系统。

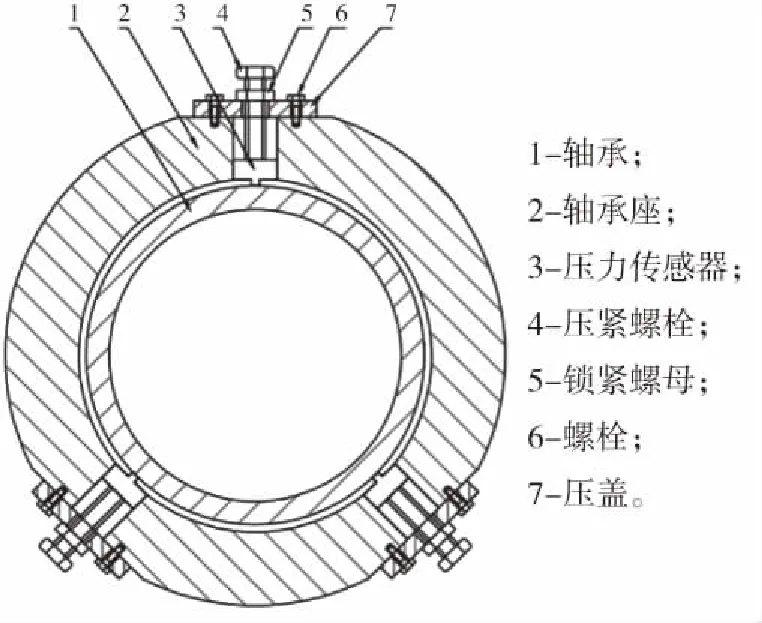
图6 径向力测量装置

该装置能够在有限的空间中，完成径向力的测量。与水泵轴承座和滚动轴承均为刚性连接，转子运转稳定，测试数据更加准确。

4.2 实验结果与数据分析

该离心泵径向力的实验值如表2所示，比较实验值与数值模拟得到的数值，并作出F-Q曲线，如图7所示。

表2 径向力试验数据

图7 数值模拟与试验比较图

由图7可知：

1)当流量Q=0.7Qn、0.85Qn、1Qn、1.1Qn、1.25Qn时，预测值相对于试验值的误差分别为6.76%、4.04%、2.08%、0.7%、8.1%，平均误差为4.34%，可知预测值是在误差允许范围内的。

2)在设计工况附近，误差最小，小流量和大流量工况下误差较大。这可能是由于在数值模拟过程中简化了物理模型，导致小流量和大流量工况下复杂的流动形式影响了数值模拟的计算精度，使得误差较大。

5 结论

1)本文采用数值模拟的方法，针对离心泵叶轮的径向力进行研究。随着流量的增加，测得的径向力先变小后变大，其中当流量为设计流量时，叶轮所受径向力最小。

2)对该离心泵进行了径向力实际测量实验，得到其各流量工况下的径向力数值，比较其与数值模拟得到的径向力数值，发现数模拟值要比实验值略高一些，且两者之间的最大相对误差为8.1%，满足数值模拟的计算误差要求，说明本次实验的数值模拟能够准确的预测离心泵的径向力。