基于机器学习的燃煤锅炉燃烧效率在线计算

陈 波 ，曹歌瀚，黄亚继 ，岳峻峰 ，徐文韬 ，王亚欧，李雨欣，金保昇

(1.江苏方天电力技术有限公司 江苏 南京 211102；2.东南大学 东南大学 能源热转换及其过程测控教育部重点实验室，江苏 南京 210096)

0 引 言

随着信息技术的发展和新基建理念的提出，传统火力发电厂亟需向智能化方向升级[1]。利用人工智能算法构建电厂锅炉的燃烧模型是目前的研究热点。锅炉效率是衡量锅炉运行状态的重要指标，也是锅炉燃烧优化的重要目标。传统的锅炉优化方法主要通过专家经验，采用交叉试验或单因素轮回试验对燃烧工况进行优化调整[2-3]，不仅费时费力，而且试验工况有限，一旦锅炉煤种或运行状态发生变化，原有的优化试验结果即失效。因此为了更好地对锅炉效率进行优化，采用启发式算法对锅炉进行参数寻优是目前较好的方法之一，要求首先构建锅炉运行参数与锅炉效率之间的实时计算模型。应明良等[4]提出了一种基于锅炉有效输出热量和总输出热量计算锅炉热效率的方法，该方法无需进行煤质测试，具有良好的实时性，但其依赖于对过热蒸汽与再热蒸汽的测量，大型设备需安装大量测点。王诣[5]针对锅炉效率计算中灰渣含碳量难以获得的问题，研究了基于图像处理技术的灰渣含碳量快速检测系统，并对锅炉效率反平衡计算进行简化分析，建立了锅炉效率的实时计算模型。赵国强[6]利用极限学习机方法对锅炉烟气含氧量和飞灰含碳量建模，将结果输入锅炉热效率计算模型，得到实时的锅炉效率计算结果。也有学者采用机器学习算法对锅炉效率进行计算，如混合最小二乘支持向量机[7]、分布式极限学习机[8]、神经网络[9-12]、支持向量机[13-14]等，这些研究将锅炉效率直接作为机器学习模型的输出，但实际的锅炉效率获取较困难，导致训练样本不足，难以获得具有广泛性的计算模型。这些研究促进了电厂锅炉智能化运行的发展，但其自身的不足限制了智能算法的广泛应用。

为了获得具有广泛性的实时锅炉效率计算方法，本文利用遗传算法改进神经网络算法训练锅炉参数与锅炉排烟温度、飞灰含碳量和煤质灰分之间的关系，计算锅炉的烟气热损失与固体不完全燃烧热损失，并对文献[4]提出的锅炉效率计算方法进行改进，减少计算模型所需的测量数据，降低锅炉的改造成本。

1 目标锅炉与燃烧系统

锅炉特征参数的选择对构建锅炉效率的计算模型十分重要，本文采用某电厂1 000 MW超超临界锅炉为研究对象，单炉膛，Π型构造，已装备低NOx同轴燃烧系统，如图1所示。燃烧系统具有一层分离燃尽风和6层燃烧器，分别对应6个磨煤机，每个磨煤机与2层燃料空气(FA)和一次风出口连接。每个燃烧器中间注入油辅助空气(OA)，下层和上层也分别注入两级辅助空气(AA)，2个燃烧器顶部是紧凑燃尽风(CCOFA)。 6个燃烧器分别记为A～F。F层的辅助空气记为F-AA-1和F-AA-2、油辅助空气记为F-OA、燃料空气记为F-FA-1和F-FA-2，其他层以此类推，F-FA-1和F-FA-2位置由一个测点测量。锅炉的过热段和再加热段产生蒸汽，过热段包含一、二、三级过热器，再热段包含一、二级再热器。燃烧器布置在4个角落，通常同一层上4组燃烧器的风门同步运行。挡板的制动以及当前位置的测量直接在炉壁内设备的机械驱动器内进行。

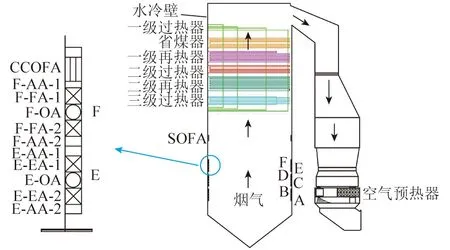
图1 锅炉示意和风门挡板排列Fig.1 Schematic diagram of the boiler andthe arrangement of the damper

选取表1中1～51号参数作为样本特征，其中，负荷代表锅炉不同发电负荷下的工况，炉膛氧量表示氧量对锅炉燃烧的影响，煤粉温度、一次风温和二次风温与锅炉的燃烧情况相关，4～49号参数为锅炉配风方式对锅炉燃烧的影响；飞灰含碳量、煤质灰分与排烟温度作为样本的因变量参与锅炉效率的计算。

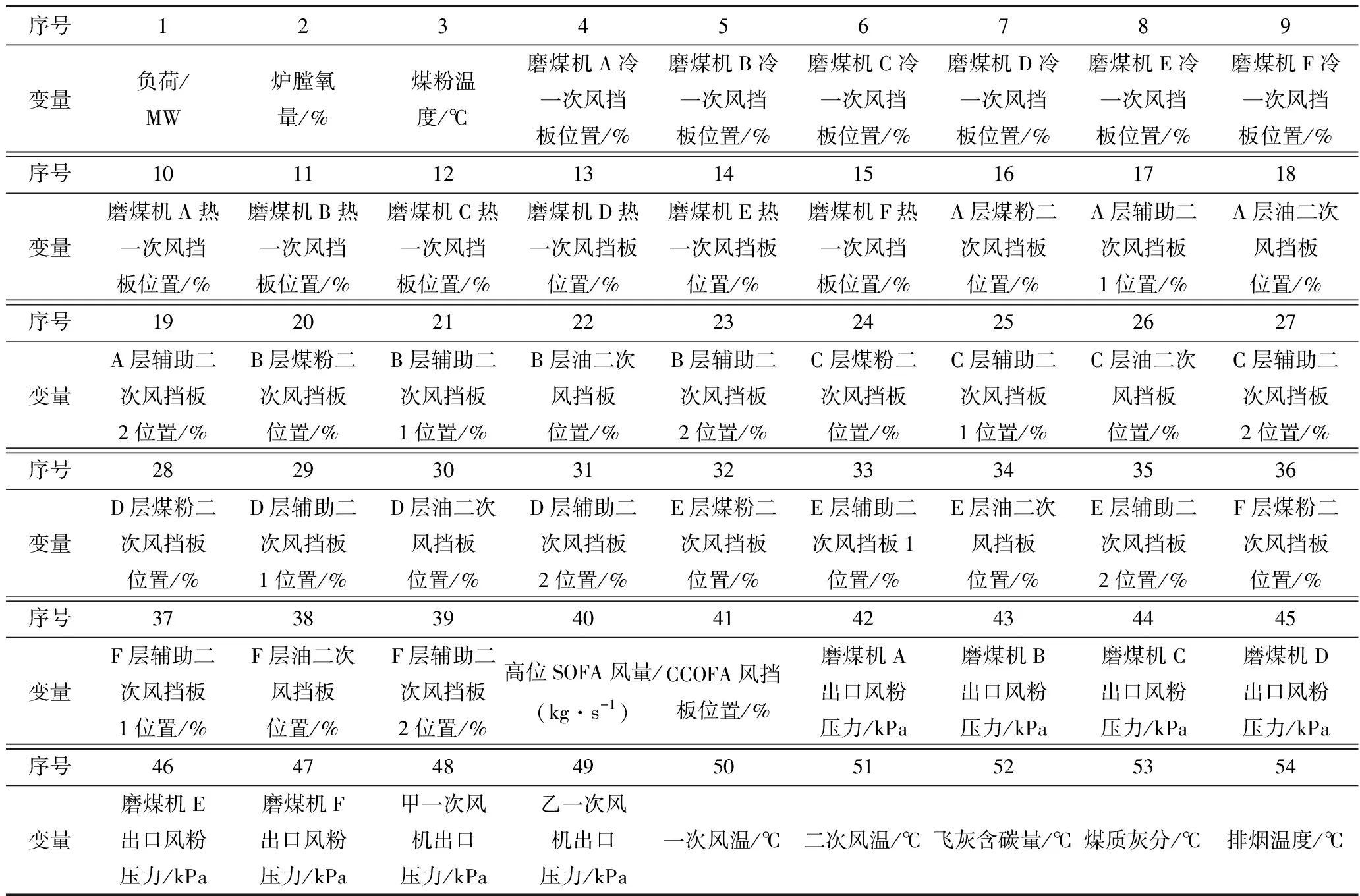
表1 样本特征

2 数据预处理

从实际电厂中获取原始数据后需经预处理才能应用于模型计算。本文数据处理包括剔除异常值、判别稳态工况与相似度处理3部分。由于故障或测量仪器原因，直接采集的数据通常存在与相邻数据点差异较大的明显异常点，采用基于数学统计学的3σ原则剔除异常值：假设某一样本含有n个数据，平均值为μ，标准差为σ，则数据分布在3σ区间的概率为99.74%。若某一数据与μ的差值大于3σ，则判定其为异常值。电厂为了适应用电需求变化，机组的负荷也会发生变化，稳态工况会受到破坏。锅炉的非稳态工况一般无法准确反映输入量与被输入量之间的关系，若直接用于建模，会对模型预测精度产生严重影响，因此，建模前需要判别稳态工况、筛选稳态工况点。本文利用滑动窗口法判别稳态工况，通过选择某一合适的窗口宽度并进行滑动，计算每次滑动后窗口内数值的标准差，若标准差过大，则该点处于非稳态工况。根据电站锅炉性能试验规程，1 000 MW锅炉机组稳态蒸发量最大允许波动范围为±2%。窗口内负荷波动低于2%时，认为窗口内工况稳定。对于已完成异常值与非稳定工况点剔除的数据，由于数据样本量较大且样本点均处于稳定工况，存在样本间数据变化微小、相似度高的情况。为优化建模训练样本，降低模型的计算量，需要对其进行相似度处理，剔除冗余信息。采用相似度函数判别样本间的相似度，设置相似度函数为

Rij=e-‖xi-xj‖2，

(1)

式中，Rij为第i组与第j组训练样本的相似度；xi、xj为训练样本中第i组和第j组数据。

采集2020-02-06—03-22每天间隔1 min的66 240条数据作为原始数据，经剔除异常值处理后，样本数据减为65 299条；经稳态判别后，样本数据为30 720条，经相似性处理，筛选出3 445组样本数据用于建模。数据处理流程如图2所示。

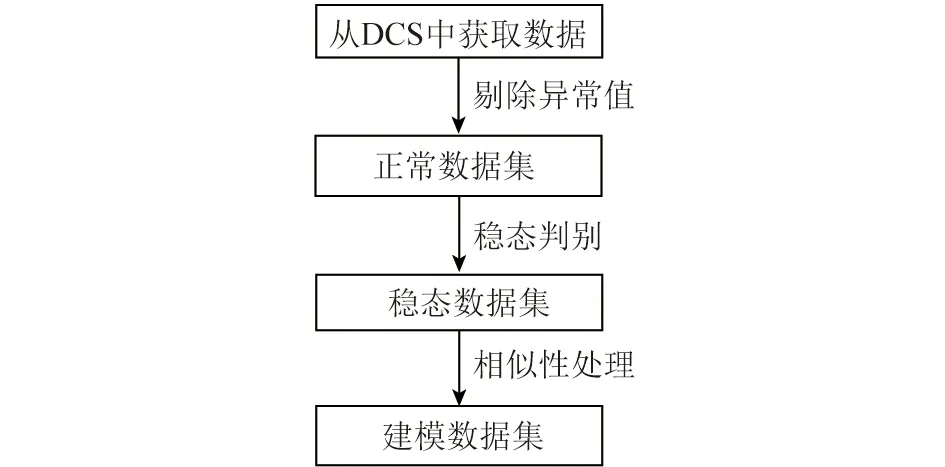
图2 数据处理流程Fig.2 Flow chart of data processing

3 锅炉效率计算

为了对锅炉效率进行优化，建立锅炉运行参数与锅炉效率之间的实时计算模型十分重要。文献[4]提出了一种基于锅炉有效输出热量和总输出热量的锅炉效率计算方法，实时性强，但该方法依赖于对过热蒸汽与再热蒸汽的测定，需安装大量测点，安装与维护成本较高，部分电厂不具备相关条件。本文锅炉效率计算公式为

(2)

(3)

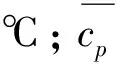
排烟温度、飞灰含碳量和煤的灰分数据由建立神经网络模型计算得出，由于神经网络模型的初始连接权值和阈值的选择对网络训练的影响很大，但又无法准确获得，因此采用基于遗传算法改进的BP神经网络算法对飞灰含碳量和煤质灰分进行预测建模。

固体不完全燃烧热损失Qs计算公式为

(4)

式中，Cfh为飞灰含碳量，%；F为耗用原煤量，kg/s，32 700为纯碳的发热量，kJ/kg。

锅炉输入热量的计算公式为

Qr=BQnet,art，

(5)

其中，B为入炉原煤量；kg/s。Qnet,ar根据燃料的高位热值与其理论空气量间近似正比的关系进行计算[15]。

(6)

式中，Qgr,ar为入炉煤的高位热值，kJ/kg；k1为绝大多数煤高位热值对低位热值的比例关系，为1.03～1.06；k2为高位热值与理论空气量的比例系数，为2.994～3.165；W为锅炉运行总风量，t/h;Δα为漏风系数，为0～0.1；ρ(O2)为锅炉运行氧量，%。

4 遗传算法改进的神经网络模型

神经网络模型是克服燃煤锅炉建模时多变量互相耦合、互相影响的有效办法[16]。BP神经网络是一种信息正向传播、误差逆向传播的神经网络，通过反向传播不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络结构简单、可调整的参数多、训练算法多、可操作性好，但其存在如收敛速度较慢、易陷入局部最小点等缺陷，且网络训练受初始连接权值及阈值的影响较大，无法准确获取，因此，考虑引入遗传算法对神经网络进行优化。

遗传算法(GA)是一种智能算法，可通过模拟自然演化过程来搜索最佳解。遗传算法优化神经网络的步骤为：首先随机初始化神经网络的权值和阈值作为初始种群，解码后赋给新建的BP神经网络，将BP神经网络的测试误差作为种群适应度代入遗传算法的进化过程并生成新的种群，将新的种群加入BP神经网络进行训练，直至网络的测试误差满足终止条件。

根据表1选取的样本特征，建立3套51-13-1的神经网络模型，即输入层神经元数量为51，隐含层神经元数量为13，输出层神经元数量为1。神经网络结构如图3所示，利用Matlab的神经网络工具箱构建网络，采用可最小化平方误差和权重的TRAINBR作为训练函数，选择TANSIG作为传递函数，选择MSE作为性能函数，选择LEARNGDM作为适应学习函数。采用遗传算法优化神经网络，最大进化代数设置为300，种群规模为100，交叉概率为0.9，变异概率为0.1，算法流程如图4所示。

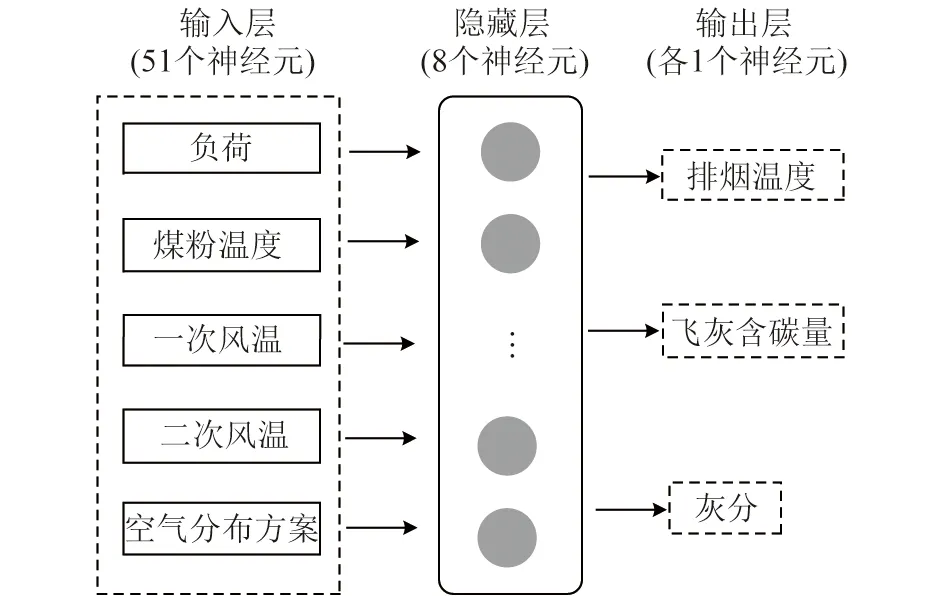
图3 神经网络结构Fig.3 Structure of Neural network

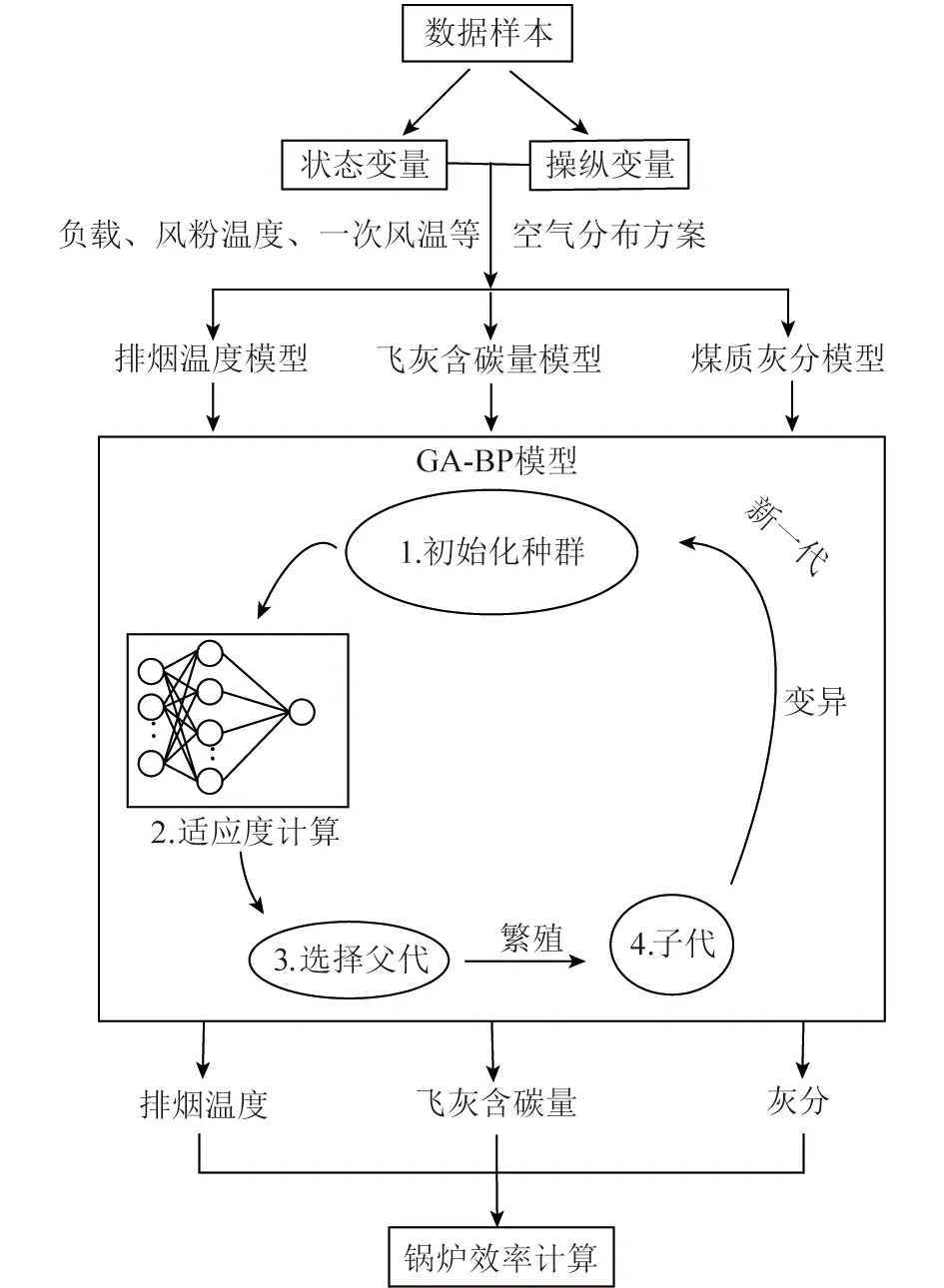
图4 锅炉效率计算流程Fig.4 Flow chart of boiler efficiency calculation

5 结果与分析

在电厂实际生产过程中，同一天的飞灰含碳量与煤质数据只能进行离散采样，因此选取取样点时刻周围的样本对飞灰的含碳量和煤质灰分进行训练。在训练神经网络模型时，随机将样本数据划分成训练集和测试集，训练集和测试集的划分比例为7∶3。图5为遗传算法优化后的神经网络模型的验证结果。表2为精度计算结果(RMSE为均方根误差，MRE为平均相对误差，MAXE为最大绝对误差)。计算方法如下：

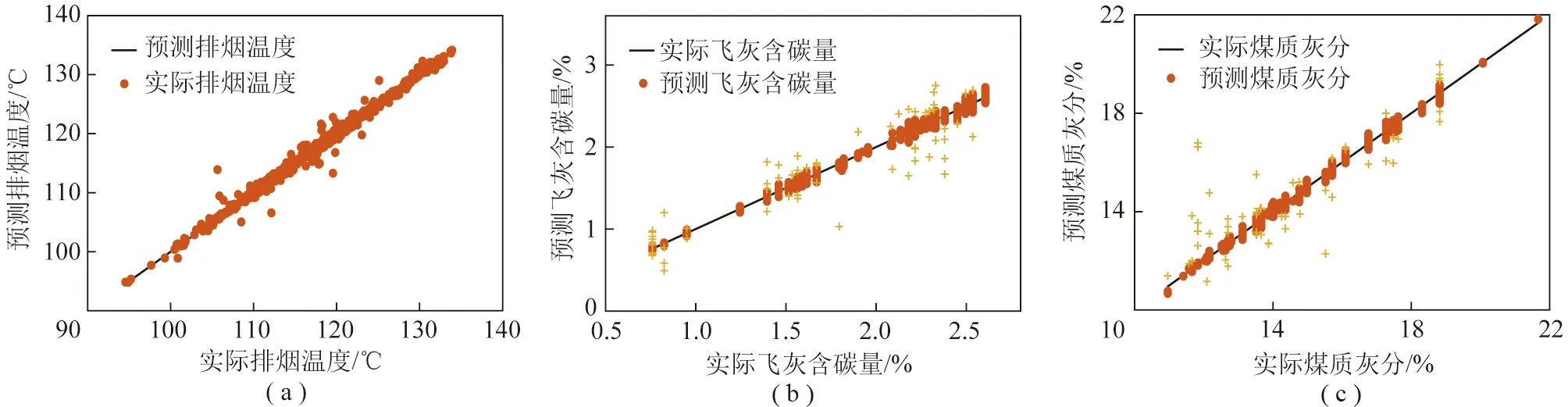
图5 排烟温度、飞灰含碳量煤质灰分测试样本的验证结果Fig.5 Validation results of exhaust gas temperature，carbon content in fly ash and coal ash test samples

(7)

(8)

(9)

由表2可知，预测结果可满足大部分样本的预测需求。对于飞灰含碳量与煤质灰分，部分结果与预期相差较大，这是由于在实际生产中，飞灰含碳量

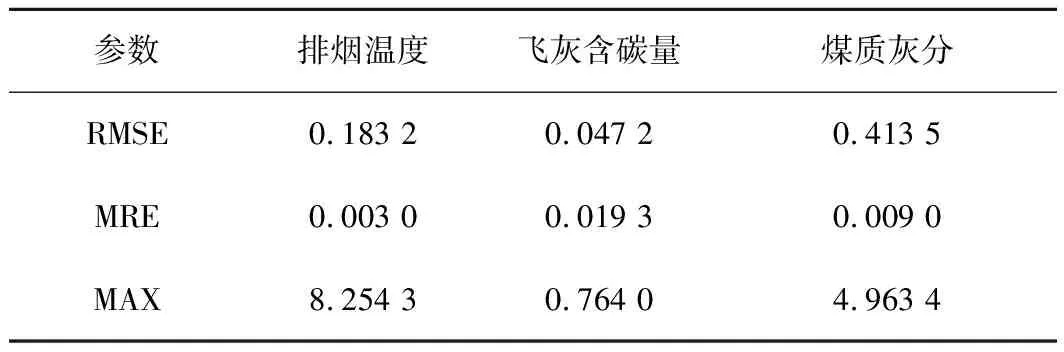
表2 BP-ANN的精度

与煤质数据测试次数较少，为了充分利用电厂的运行数据，将某一时刻的测试数据扩展到其他时刻，因此造成部分样本数据偏差较大。以实际的测试数据为基准，3倍平均相对误差为范围，图5(b)、(c)中超过实际测试数据3倍平均相对误差的预测数据标记为“+”，被标记的数据视为由于数据推测引起的误差。飞灰含碳量的测试样本中的推测误差数据占7.07%，煤质数据测试样本的推测误差数据占5.13%。

图6为电厂某一天的锅炉效率随时间的变化(R为实际蒸发量与额定蒸发量的比值)。可以看出，锅炉效率与实际蒸发量的变化近似一致。锅炉的实际蒸发量下降时，锅炉效率降低，这可能与锅炉蓄热有关，负荷降低导致锅炉的单位煤量烟气量增加，但排烟温度未降低，使烟气热损失增大，锅炉效率突然降低。另外，锅炉的实际蒸发量在60%以上额定蒸发量时，锅炉效率易保持在较高水平。

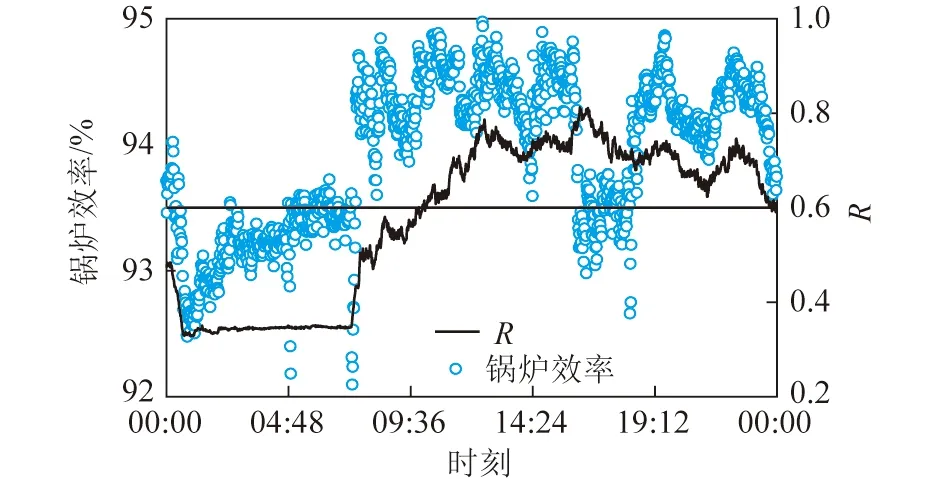
图6 电厂的锅炉效率与实际蒸发量随时间变化Fig.6 Change of boiler efficiency and actualevaporation of power plant with time

6 结 论

1)对所运行的锅炉进行分析研究，选择合适的锅炉燃烧运行特征作为样本特征。

2)根据特征采集相应数据，并对数据进行剔除异常值、判别稳态工况和相似性处理，减少了用于模型训练的数据量。

3)利用遗传算法改进的神经网络算法计算排烟温度、飞灰含碳量与煤质灰分，进而计算出锅炉的排烟热损失与固体不完全燃烧热损失，代入锅炉效率的反平衡计算模型中得到锅炉效率。计算所得的锅炉效率变化与实际蒸发量变化近似一致。锅炉的实际蒸发量下降时，锅炉效率降低。锅炉的实际蒸发量在60%以上额定蒸发量时，锅炉效率易保持在较高水平。

4)计算结果表明该方法可操作性与实时性强，且精度符合预测需求，可满足电厂对锅炉效率的日常监测要求。