移动式颗粒床气固分离性能冷态试验

樊英杰，刘今乾，马 琛，郭 伟，杨伯伦，吴志强

(1. 西安交通大学 化学工程与技术学院 陕西省能源化工过程强化重点实验室，陕西 西安 710049；2.陕西煤业化工技术研究院有限责任公司，陕西 西安 710065)

0 引 言

“富煤、少油、缺气”的能源结构特点决定了煤炭在我国将长期处于能源消费的主导地位，为此，煤炭资源的分级高效利用是确保我国能源安全的重要途径之一[1]。采用热解技术进行煤炭分质转化可在较低温度下实现煤炭资源的高效分质利用，但热解产物包括各种粉尘颗粒，因此需要进行粉尘脱除。含尘含油高温热解气净化是粉煤热解技术工业化过程中需要迫切解决的问题[2]。针对高温热解气的净化，国内外学者提出了旋风分离[3]、电除尘[4]、颗粒床除尘[5]等处理方式，其中颗粒床技术具有过滤介质对气体和灰尘性质不敏感、可选择性较多等优势，引起广泛关注。虽然相关企业已对颗粒床除尘技术进行积极布局，但总体上该技术尚处于初期研究阶段[6-7]。

王苗等[8]对影响旋风-颗粒床过滤器两级除尘性能的过滤介质尺寸、厚度以及氮气流量等因素进行了探索，发现影响除尘性能的关键因素为表观气速，其次为过滤介质粒径，氮气流量影响有限，滤料粒径0.38～0.83 mm 时，颗粒床过滤器平均除尘效率97.18%。付金壮等[9]比较了入口粉尘浓度和再生尘源浓度对旋流-颗粒床耦合分离器性能的影响，指出2者对床层的压降影响显著，而入口粉尘浓度对整体的除尘效率影响有限，入口浓度在5.95～59.13 g/m3时，试验稳定后分离效率可达98%。吕涵等[10]使用冷模气固顺流式移动床过滤器，通过改变表观气速、颗粒循环强度、粉尘的比沉积率等参数研究其对床层压降和除尘效率的影响，表观气速为0.126 m/s、比沉积率σ为0.000 735时，过滤器的操作压降可达相对稳定状态，此时除尘效果最优，捕集效率达97%以上。王助良等[11]研究指出，影响颗粒床过滤器除尘效率的关键因素是沉积粉尘，通过分析孔隙率在颗粒层过滤过程中的变化可得到气流含尘质量浓度、灰尘沉积密度等在颗粒层内的变化规律以及除尘效率的关联式。Chen等[12-13]对移动颗粒床过滤器进气系统的设计和测试程序进行研究，包括气体流量、进气系统几何形状、流量校正插件在滤床上的位置等参数对过滤系统性能的影响，并分析了进气系统和滤床中气体的动力学模型与流动性。

通过数值模拟方式探究移动床过滤性能，可在一定程度上降低试验成本，赵建涛等[14]采用二维错流数学模型研究了移动颗粒床过滤器除尘过程的气体流动规律、粉尘沉积特点以及气体含尘浓度变化过程，并通过高温煤气除尘试验对模型进行验证，表明表观过滤气速0.1～0.3 m/s时，除尘过程的操作压降和除尘效率的模型计算值和试验结果基本吻合，但更高气速下，由于颗粒层内出现空穴、贴壁等非正常流动现象，模型计算误差较大，超出模型适用范围。刘鹏等[15]建立了除尘器的气固两相流场的数学模型，研究了双层滤料颗粒床高温除尘器中挡板气流通道宽度、挡板层数与高度变化对除尘效果的影响。陶初炯等[16]通过改变大型颗粒床除尘器过滤介质与壳体温度以及预热时长，对含尘热解煤气除粉前的预热过程进行模拟分析，研究结果为该技术的应用提供一定的数据基础。

为满足粉煤热解含尘气体高效净化技术工业化应用的要求，需进一步明晰粉煤热解高温烟气净化的移动式颗粒床操作压降、除尘效率等工艺设计指标和操作参数之间的关联规律，但目前该研究较少，需通过以下3个方面进行深入研究：① 保证滤料的循环稳定，设备的稳定性及高温的结焦问题；② 进气过程造成局部二次夹带，需优化颗粒床内部结构；③ 移动式颗粒层过滤因素的整合，得到滤料循环、过滤厚度及进气速度最优解。本文针对粉煤热解含尘气特点，设计和搭建了移动床颗粒层过滤除尘冷态试验平台，通过正交试验设计，综合研究了各因素对颗粒层过滤效率和系统压力降的影响规律，分析除尘效率和床层压降与颗粒床特性、操作条件之间的内在关系，在试验结果和理论计算的基础上提出颗粒层过滤性能的改进措施，获得颗粒床除尘装置高效稳定的除尘工艺参数，为粉煤热解含尘煤气颗粒床热态除尘装置的设计以及工艺操作优化提供依据。

1 试 验

1.1 工艺流程

颗粒床除尘系统由含尘气体发生器、旋风除尘器、颗粒床、布袋除尘器、滤料循环再生装置和仪表控制等组成，如图1所示。除尘操作步骤为：风机运行产生动力风将含尘气体引入旋风除尘器，含尘气体经旋风除尘器预除尘后流经颗粒床层，大部分粉尘通过与颗粒层的碰撞、吸附、拦截作用而从气体中去除[17]。称取适量粉尘加入料斗，根据下料量将粉尘螺旋给料机调至所需转数。根据选定的过滤颗粒下料速度，确定合适提升机滤料提升速度、旋转下料机频率，并对空滤袋进行称重并记录。将风机1与风机2频率调至所需数值后运行，同时打开粉尘螺旋给料机与提升机，观察风压并记录。试验结束后依次关闭粉尘螺旋给料机、提升机，旋转下料机，拆除滤袋称重取样，并对灰尘料斗内灰尘进行称重。

图1 颗粒床冷态试验装置Fig.1 Cold experimental device of granular bed

1.2 滤料与尘样

过滤介质的特性对过滤式除尘过程非常重要，其成本通常占整个系统投资的10%～15%。过滤介质的材质、质量和有效运行时间会对除尘器效率、运行阻力以及设备养护周期等有重要影响。优质过滤介质应具有耐磨、耐腐、价廉、易得等特点，且介质对高温气体的耐热性能也很重要。本文以冷态试验为主，经综合分析各类过滤介质颗粒尺寸、成本、是否易得等，选择小麦作为颗粒床冷态试验滤料，其粒径为3.5～6.0 mm，孔隙率为0.39，堆积密度为0.75 kg/m3，真密度为1.23 kg/m3。

模型粉尘物需与实际粉煤热解粉尘具有尽可能相近的物理性质，且需具有分布均一的尺寸和稳定的材质，保证颗粒可长时间储存在工作环境中。基于此，选择硅胶作为试验粉尘，其15 μm以下颗粒占3.76%，中位粒径颗粒为66.10 μm。

1.3 关键参数计算

过滤效率指过滤层过滤气流粉尘的效果，是权衡除尘器成效的基础指标。具体定量表达指在试验气流流经过滤器的过程中，除尘器捕获的粉尘量占进入设备粉尘量的比例，可由设备的进出口气体浓度变化计算得出。

(1)

式中，η为过滤效率，%；C1、C2分别为进、出口气体含尘浓度，g/m3。

C1=60m/Q1，

(2)

式中，m为单位时间螺旋下料机的下料量，g/min；Q1为颗粒层截面的风量，m3/h，可通过运行风机对螺旋下料机进行标定得到。

uf=Q1/S，

(3)

式中，uf为表观过滤风速，m/s；S为颗粒层截面面积，m2。

过滤器进、出气口气流的全压差即为过滤的总压降。通过研究除尘器过滤过程中的压降，可获得改进除尘器结构、减少设备运行阻力的指导性思路。鉴于本文的试验设备具有相同的进、出气口管道段面积，故只需测量颗粒层进、出气口侧管道上测压点间的静压降即可。

ΔP=P2-P1，

(4)

其中，ΔP为过滤层总压力损失，Pa；P2为颗粒层出气口侧流体静压值；P1为颗粒层进气口侧流体静压值。在颗粒床层进气连接管、出气管以及颗粒床层内部各安装一个静压环，使变径、弯头等局部阻力可基本忽略。4个压力测试点数据分别通过压力传感器传送到仪表盘，通过计算得出压差，即过滤压力损失值。

1.4 试验工况设计

在选定过滤粉尘及颗粒层填充料的基础上，错流移动式颗粒床的除尘效率主要受过滤层厚度h、表观过滤风速uf、滤料下落速度u1(单位时间滤料在过滤床层下落的长度)控制。其中表观过滤风速主要受风机1风量Q1(风量Q1由风机1频率f确定)的影响，故选取滤层厚度h、滤料下落速度u1、风机1频率f作为正交试验的三因素，通过L9(33)三水平正交法设计试验。过滤截面为0.50 m×0.15 m，假设截面风速相等，通过计算可得表观过滤风速范围为0.29～0.41 m/s。表1为过滤效率正交试验因素水平，表2为具体工况。

表1 正交试验因素水平

表2 过滤效率正交试验设计方案

2 试验结果与分析

2.1 过滤效率

表3、4分别为不同工况颗粒床的过滤效率，可知对过滤效率影响最大的参数是表观过滤风速，同时风量Q1变化也将导致过滤效率产生相应的波动，滤层厚度与滤料下落速度引起的过滤效率波动程度相近。通过过滤效率方差分析可得出，表观风速为过滤效率的最主要影响因素，过滤层厚度其次，最后为滤料下落速度。最优水平为A3B1C1，即滤层厚度为300 mm，风机1频率为35 Hz，滤料下落速度为0.002 m/s。

表3 过滤效率分析

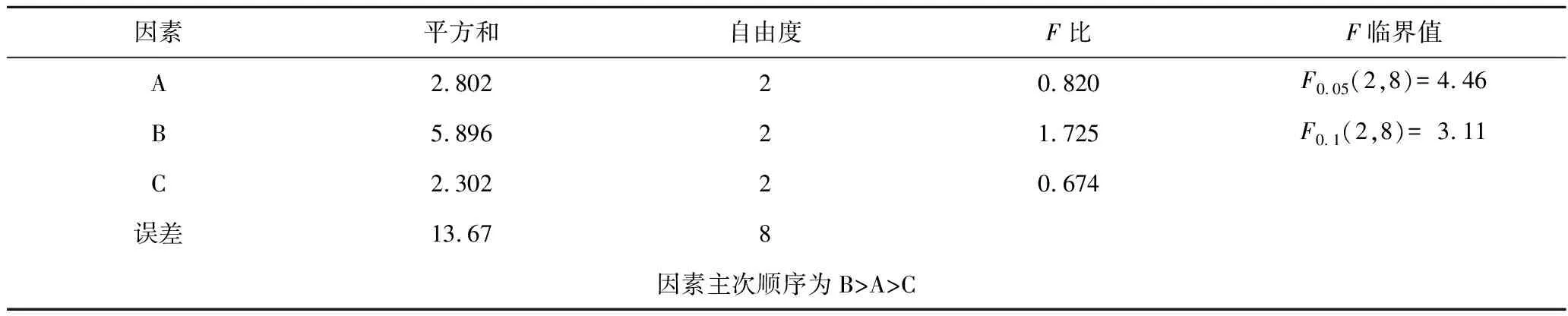
表4 过滤效率正交试验方差分析

各因素、水平的过滤效率变化如图2所示，可知随着过滤层厚度增大，过滤效率逐渐增加，达到一定厚度后过滤效率变化不明显；表观过滤风速和滤料下落速度变大时，过滤效率降低，原因在于随表观风速加大，更多粉尘被气流携带走，导致过滤效率降低。增大滤料下落速度后，滤料运动的不均匀性增加，导致滤料间的空隙加大，粉尘更易穿过床层，导致颗粒床过滤效率降低[8，10]。

图2 各因素、水平的过滤效率变化Fig.2 Filtration efficiency of three factors and three levels

2.2 最优条件下的过滤效率

正交试验得到的最优条件下的过滤效率可达98.1%，采用激光粒度仪测定试验前后气体中的粉尘粒径(表5、图3)。过滤后的粉尘粒径范围比过滤前更宽，多1.4～3.3 μm及208.9～831.7 μm粒径段，前者占比0.91%，大于208 μm粒径段占比为0.049%。

图3 过滤前后粉尘粒径分布Fig.3 Particle size distributions of dust before and after filtration

表5 过滤前后粉尘粒径情况

通过计算可以得到的分段过滤效率见表6，其中0～5 μm的过滤效率较低，为90.03%。分段过滤效率随粒径增大而提高，大于15 μm粒径的过滤效率基本在98%以上。对不同粒径范围的过滤效率进行计算可知，过滤分级效率在粉尘小粒径段变化明显，3.80 μm以下的过滤效率只有19%(图4)，3.80～10.0 μm粒径段的过滤效率升至96%，粒径大于10 μm后，过滤效率基本在98%以上。过滤效率随粒径变化的原因可归结为不同粒径的过滤机理差异：粒径较小时，主要是扩散沉积、静电吸附机理等起主导作用，故随着粒径减小，分级过滤效率逐渐增大；粒径达到一定值后，过滤效率的主要影响因素是惯性碰撞和直接拦截，分级过滤效率随粒径的增加而增大[3，12]。

表6 最佳操作条件下冷态试验分段过滤效率

图4 分级过滤效率曲线Fig.4 Graded filtration efficiency curve

2.3 粉尘浓度对过滤效率的影响

在最优试验条件下(风机1频率为35 Hz，风机2频率为40 Hz，滤层厚度300 mm，滤料下落速率0.002 m/s)，过滤时间10 min，粉尘螺旋下料机转速分别为600、800、1 039、1 200、1 400 r/min。粉尘浓度对过滤效率的影响见表7。粉尘浓度较小时，过滤效率随粉尘浓度的增加而增大，达到一定值后，过滤效率随粉尘浓度的增大而减小。主要是因为粉尘浓度增大时，主要影响因素有滤料碰撞拦截和二次扬尘，前者起到主导作用时，过滤效率随粉尘浓度的增加而增大；后者起主导作用时，过滤效率随粉尘浓度的增大呈减小趋势。粉尘下料转速为1 039 r/min时，基本达到过滤效率最大值，为98.1%，这与文献[2]的固定床、移动床颗粒过滤技术的过滤效率相近，过滤效果较好。

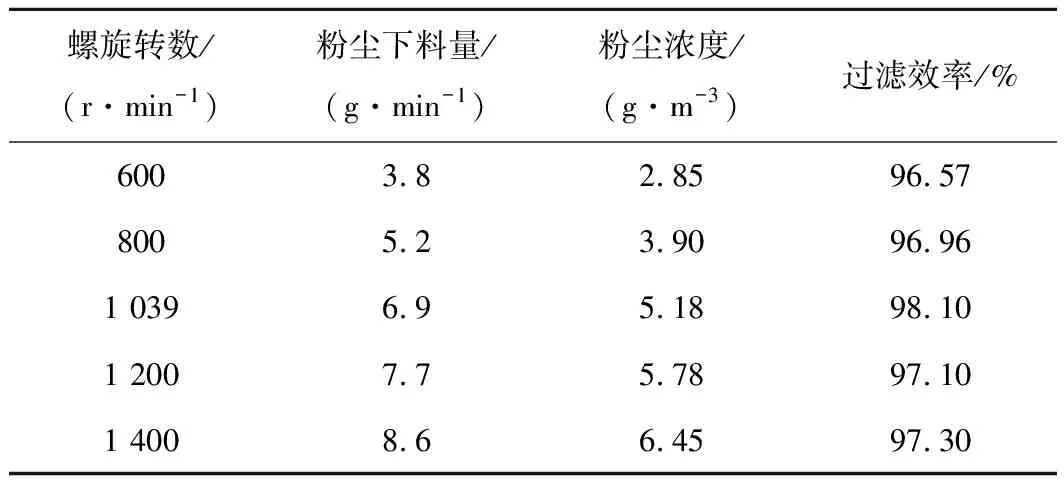
表7 过滤效率与粉尘浓度的关系

2.4 过滤效率表达式回归分析

在20 ℃、空气黏度μ=1.789 4×10-5kg/(m·s)、空气密度ρ=1.225 kg/m3、粉尘浓度C=4.4 kg/m3、滤料平均粒径dp=4.5×10-3m条件下，过滤效率的计算公式为

η=1-exp(b0hb1ufb2u1b3)，

(5)

对各物理量的量纲无因次化简得

(6)

两次取对数后得

(7)

代入数值，简化计算可得

(8)

多元回归分析后可得出过滤效率的多元非线性回归方程为

(9)

其中，0.1 m≤h≤0.3 m，0.29 m/s≤uf≤0.41 m/s，0.002 m/s≤u1≤0.008 m/s。

正交试验测量值与回归公式计算值的对比如图5所示，可以看出，过滤风速最低、过滤层的滤料厚度为300 mm、滤料循环速度为0.002 m/s，过滤时间为10 min，初始粉尘浓度为4.4 g/m3时，试验过滤效率为98.1%，回归公式计算值为98.07%，两者基本相符。

图5 过滤效率试验值与预测值比较Fig.5 Filtration efficiency comparison of test and predicted values

3 结 论

1)通过结合正交试验极差分析与方差分析，得到冷态试验中表观风速为过滤效率最主要的影响因素，其次是过滤层厚度和滤料下落速度。过滤效率随表观风速和滤料下落速度的增大而减小，随着过滤层厚度的增加而增大。过滤层厚度增至200 mm以上时，过滤效率变化较小。

2)最优过滤条件为过滤风速最低、滤料厚度为300 mm、滤料下落速度为0.002 m/s，过滤时间为10 min，此时过滤效率为98.1%。过滤分级效率在粉尘小粒径段变化明显，粒径3.80 μm以下的过滤效率仅19%；粒径大于10 μm后过滤效率基本在98%以上。移动式颗粒床冷态过滤试验中床层压力变化不大，整个试验过程近似稳定。

3)利用回归分析得到过滤效率与过滤层厚度、滤料移动速度、表观过滤速度的关联方程，为颗粒床设计以及移动颗粒层过滤性能的预测提供依据。