地震条件下引水隧洞动力响应分析

叶 茂，耿金平，袁永康

(1.江苏省工程勘测研究院有限责任公司，江苏 扬州 225000；2.溧阳市竹箦水利站，江苏 溧阳213300)

近年来随着经济的不断发展，我国大力兴建水利工程，以更好地保障人民的生产生活。水利工程建设过程中，大多会涉及到引水隧洞工程，而引水隧洞工程建设的成功与否很大程度上决定着水利工程的建设安全[1-2]。当工程所处坝址地震烈度较高时，为了保证引水隧洞的安全，需要进行考虑地震荷载作用下的硐室稳定性研究，其方法包括拟静力法、Newmark 滑块分析法、概论分析法和数值分析法等[3-4]。某隧洞工程所处区域各构造体系在地质发展历史中经历了多期强烈构造变动，所处区域地震烈度高，总体位于 7～8度抗震设防烈度。本文针对该隧洞工程，在优选硐室形状和支护方案的基础上，运用数值模拟方法，采用 FLAC3D中的基于显式差分的完全非线性分析理论，合理选择输入激励(频谱、振幅、持时)、岩土参数、本构模型、透射边界、模型网格等进行地震动力模拟，从而作出引水隧洞的稳定性评价，以期分析成果和研究方法可以为其他相关隧洞工程设计提供参考与借鉴。

1 地下硐室动力时程分析方法

1.1 场地人工地震波的选取与合成

当前，国际公认的地震动三要素为地震动强度、地震动频谱特征和地震动持续时间。在选用地震波时，地震动三要素都要考虑，并根据情况加以调整。FLAC3D允许的动力荷载输入为加速度时程，速度时程、应力时程和集中力时程。对刚度较大的岩石材料，可采用地震加速度时程直接输入到模型底部。根据《水工建筑物抗震设计规范》(DL 5073-2000)，按技术标准设计的所有构筑物，均应达到50年超越概率为10%的设防烈度。本隧洞区域段设计基本地震峰值加速度为0.10 g，根据《水工建筑物抗震设计规范》(DL 5073-2000)岩基面50 m以下隧洞可选取设计基本地震峰值加速度的1/2，因此本文选用0.05 g作为基本地震峰值加速度。Kobe地震波的最大加速度为0.344 7 g，计算中必须将实际地震记录的峰值折算成所需的加速度峰值，故对Kobe加速度进行振幅变换，并对变化后的波型进行傅里叶变换分析(FFT)以及滤波和基线校正。本次模拟只选取集中大部分能量的前10 s波段进行计算。

1.2 边界条件和阻尼的设置

FLAC3D中提供了静止(黏性)边界和自由场边界两种边界条件来减少模型边界上波的反射。本次动力计算在模型的底部设置了黏性边界进行模拟。

同时实践证明，瑞利阻尼计算得到的加速度响应规律比较符合实际，故本模型中采用瑞利阻尼进行计算。瑞利阻尼最初应用于结构和弹性体的动力计算中，以减弱系统的自然振动模式的振幅。FLAC3D设置瑞利阻尼时，需要确定两个参数：最小临界阻尼比和最小中心频率。根据频谱分析结果，本模型取最小中心频率为 0.75 Hz。对于岩土材料而言，临界阻尼比一般是2%～5%，本模型中选用临界阻尼比为5%。

2 计算模型、参数与计算内容

2.1 计算模型和参数

为了模拟地震动对引水隧洞的影响，采用双洞互不影响方案，即双洞间距45 m、单洞毛洞直径约7 m的对称双洞方案，单洞具体尺寸见图1；地应力大小见表1；围岩力学模型仍采用 Mohe-Coulomb本构模型，参数见表2；采用图2锚杆布置方案，支护参数见表3。衬砌方案选用泡沫混凝土和一般混凝土的复合衬砌结构，其中衬砌的分节长度为3 m，衬砌的剪切缝宽为10 cm，均采用弹性模型，弹性模量为0.62GPa，泊松比0.41，干密度720 g/cm3。

图1 单洞尺寸示意图

图2 锚杆布置位置示意图

表1 地应力分布表(隧洞埋深为300m)

表2 围岩力学参数

表3 支护情况下所采用的参数表

2.2 计算内容

大量的研究资料表明，在模型底部施加地震波时，横向(Y方向)的影响要大于顺向(X方向)，因此计算中在模型底部Y方向施加修正Kobe地震波谱(图3)。以下分别分析了无错动、错动5a、50a和100a后发生地震时围岩和衬砌的力学响应，施加的错动量见表4。

图3 局部计算网格模型

表4 不同年限所施加的位移量表

3 支护方案综合评价

考虑即使在地震荷载作用下，由于塑性变形的存在，位移会随着地震作用时间的增长而增大。在地震结束时，位移达到最大值。因此，本次主要分析地震荷载结束时间点围岩与衬砌的动力学响应。以下仅取单洞截面进行分析。

3.1 围岩计算结果

见图4、图5。

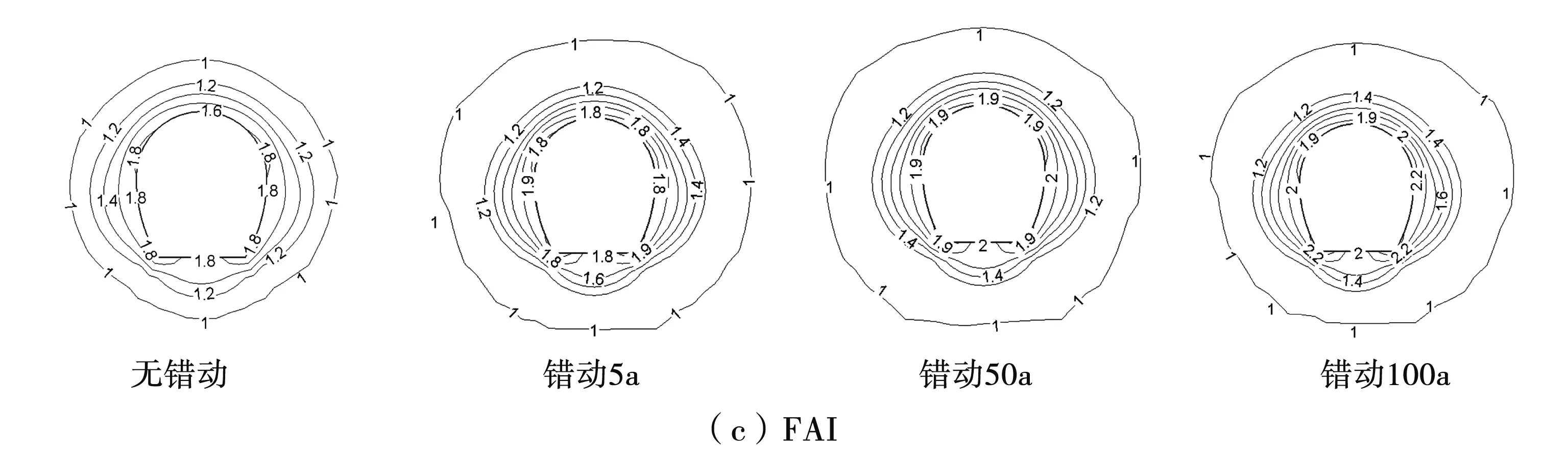
图4 衬砌分节中心位置处围岩力学响应

图5 剪切缝分节中心位置处围岩力学响应

衬砌中心和剪切缝处的围岩体随错动增长后，在地震荷载作用下变形破坏的规律为：

1) 地震波由硐室底部传至洞顶，硐室底部受地震波的震动放大作用最强，在无错动条件下，围岩的最大位移均出现在硐底与边墙；相反，洞室上部由于地震波的绕射作用，其震动强度降低，拱肩与洞顶的位移较小。如果在断层错动条件下发生地震，位移分布并不均匀，总体来说，硐室受错动影响和地震波的放大作用，最大位移出现在硐底与左边墙处。如果对比剪切缝处围岩与衬砌处的围岩位移可以看出，衬砌处的围岩位移更小，说明衬砌处的围岩整体刚度更好。见图6。

图6 不同计算条件下位移对比图

2) 即使在无错动条件下，地震波作用使围岩出现了3～4 m的塑性区。随着错动作用的增强，塑性区主要在硐底以及左硐角和右拱肩方向持续扩大；当百年错动后发生地震，围岩塑性区最大可达6～7 m。对比衬砌和剪切缝处二者的塑性区深度可以看出，后者稍高于前者，说明剪切缝的设置并不会对围岩稳定性产生显著影响。

3) 在无错动条件下，围岩各部位FAI均小于2,未出现破坏区，说明在此工况下出现地震可以保证围岩安全。随着错动的增长，发生地震后会出现破坏区，但即使错动100 a发生地震时，破坏区并未连成片。值得注意的是，在各个工况条件下，相比较其他部位，硐底的破坏更加严重，建议增强硐底支护。见图7、图8。

图7 衬砌分节中心位置处计算结果

图8 剪切缝位置处计算结果

3.2 衬砌计算结果

衬砌中心和剪切缝处的衬砌随错动增长后，在地震荷载作用下变形破坏的规律为：

1) 在无错动条件下，衬砌和剪切缝的最大位移均出现在硐底部位(拱脚)，说明也同样受到地震波的放大作用。如果在断层错动条件下发生地震，位移分布并不均匀，总体来说地震波主要集中在左拱脚和左边墙处。同样在地震动条件下，可以从图9对比看出，剪切缝处承担了更多的硐室变形，剪切缝最多可达衬砌处位移的3.5倍。

图9 不同计算条件下位移对比图(衬砌)

2) 无错动条件下，衬砌本身并未受到地震波作用的破坏，混凝土以及钢筋工作正常，剪切缝处的混凝土也工作正常；在错动5 a后发生地震，衬砌工作正常，但剪切缝处的混凝土会发生破坏，错动时间越长后发生地震，对衬砌和剪切缝的破坏就越严重(图10)；在错动100 a后发生地震，衬砌也会遭到破坏。

图10 不同计算条件下混凝土内力图

4 结 语

为了保证引水隧洞的安全，本文考虑地震荷载作用下的硐室稳定性研究， 主要运用数值模拟方法，采用FLAC3D中的基于显式差分的完全非线性分析理论，合理选择输入激励(频谱、振幅、持时)、岩土参数、本构模型、透射边界、模型网格等进行地震动力模拟，从而作出引水隧洞的稳定性评价。主要结论如下：

1) 即使在无错动条件下，地震波作用使围岩出现了3～4 m的塑性区；当百年错动后发生地震，围岩塑性区最大可达6～7 m。对比衬砌和剪切缝处二者的塑性区深度可以看出，后者稍高于前者，说明剪切缝的设置并不会对围岩稳定性产生显著影响。在各个工况条件下，相比较其他部位，硐底的破坏更加严重，建议增强硐底支护。

2) 无错动条件下，衬砌本身并未受到地震波作用的破坏，混凝土以及钢筋工作正常，剪切缝处的混凝土也工作正常；在错动5 a后发生地震，衬砌工作正常，但剪切缝处的混凝土会发生破坏，错动时间越长后发生地震，对衬砌和剪切缝的破坏就越严重；在错动100 a后发生地震，衬砌也会遭到破坏。

3) 为了保证隧洞工程的安全，有必要进行地震动力模拟，作出稳定性评价，为工程的建设提供有效建议。