基于等效一致边界的重力坝地震响应分析

戴江力

(新疆库尔干水利枢纽工程建设管理局，新疆 库尔干 832100)

坝-地基动力相互作用分析是一个比较复杂的技术课题[1-2]。在早期的大坝地震响应分析中，采用了一些简化的假定，通常采用无质量地基模型，即考虑地基作用时，略去了辐射阻尼和地震动输入的影响。无质量地基虽然可以反映地基的柔性，避免了地基质量对地震波能量的放大作用，但未考虑辐射阻尼的影响，把地震动响应作为一个封闭系统来研究，这与实际情况显然是不相符的。随着计算机有限元方法的发展，黏弹性人工边界理论逐渐成熟，在对待地基作用问题上，与传统的无质量地基相比，黏弹性人工边界则能够很好地模拟地震波能量向远域逸散的问题[3]，正确反映了坝体-坝基的整体动力特性。

1 人工边界理论

在有限域地基截断面上设置局部人工边界，工程上较多采用的有Lysme和Kulemeyer提出的黏性边界；Deek和Randolph提出的时域黏弹性边界；廖振鹏[4]提出的透射边界等。其中，黏弹性边界与同类人工边界相比，概念清楚，且易于在有限元软件中实现，是目前采用最多的地基处理方法。然而在实际问题中，有限元在实现黏弹性施加时比较繁琐，清华大学刘晶波[5-6]教授等在黏弹性人工边界的基础上推导出了等效一致黏弹性边界，简化了施加人工边界的前处理工作。

1.1 等效一致人工边界

等效一致黏弹性边界单元，该方法是在已建立的有限元模型的边界上，沿边界面外法向延伸一层厚度相等的实体单元，并将最外层边界固定。基于黏弹性人工边界可推导出三维一致黏弹性人工边界单元的刚度及阻尼矩阵，再利用单元矩阵等效原理，便可得到边界等效实体单元的材料参数。等效一致黏弹性边界单元的等效剪切模量、弹性模量以及阻尼系数分别取为：

(1)

(2)

(3)

1.2 等效节点力公式

黏弹性人工边界和等效一致黏弹性边界的等效节点力公式一致，以S波为例：

(4)

(5)

(6)

(7)

(8)

(9)

式中：ρ、cs分别为介质质量密度、S波波速；L为底边界到地表距离；Δt3=l/cs和Δt4=(2L-l)/cs分别为L节点处入射S波和地表反射S波的时间递延。等效节点上标表示所在人工界面处的外法线方向，下标代表节点号和分量方向，与坐标轴方向一致为正，相反则为负。

2 三维等效一致边界验证

基于ANSYS软件，弹簧单元采用Combin14单元，从底部人工边界模拟入射S波的动力响应，入射位移脉冲波方程为：

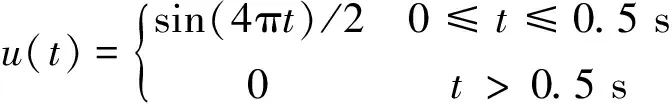
(10)

计算模型尺寸长×宽×高为400 m×400 m×600 m，网格尺寸为20 m，采用有限元单元法进行空间离散。根据刘晶波等效一致黏弹性理论证明，等效单元厚度对分析结果影响较小，为方便本次等效一致黏弹模型边界单元厚度取模型单元厚度。模型介质模量E=4.88 GPa、泊松比为0.22、质量密度2 000 kg/m3、时间步长0.005 s，历时2 s，共计算400步，见图1-图2。

图1 三维等效一致边界模型

图2 底部和顶部观测点位移时程

从图2可以看出，顶部观测点位移峰值为入射位移时程峰值的两倍。这是由于入射波传播到顶面时发生反射，波产生叠加效应，经顶面反射后入射波继续向下传递至模型底部，由于模型底部外侧设置了人工边界，波在底面不再发生反射。

3 某重力坝地震响应分析

3.1 计算模型

本文选取西南某重力坝段典型挡水坝段为研究对象，坝宽15 m，坝高97 m，上游水深83 m，下游水深3 m。坝底高程2 394 m，高程2 444 m以上采用碾压混凝土C15，坝体高程2 444 m以下采用碾压混凝土C20，基岩为二类岩石，三维有限元模型见图3。地震发生时，库水产生的地震动水压力采用附加质量法计算。分别采用无质量地基法和等效一致黏弹性人工边界，对模型进行地震响应分析，并对这两种工况地震响应结果进行对比分析。材料参数见表1。

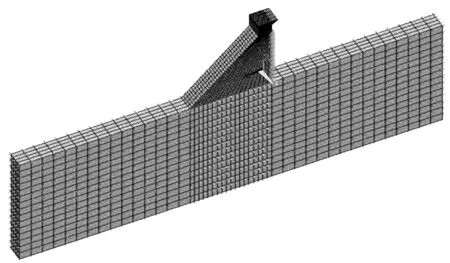
图3 重力坝三维有限元模型

表1 材料参数表

3.2 人工合成地震波

根据选取工程场址类别，地震基本烈度为8度，设计地震取100年超越概率为2%时的水平基岩峰值加速度0.316 g,按顺河向和竖直向地震组合进行计算。地震波采取人工合成方式(阻尼比为5%)，每条地震波相互独立，时间间隔为0.01 s,持时10 s。其中，竖向地震波取水平向地震波加速度峰值的2/3。见图4-图5。

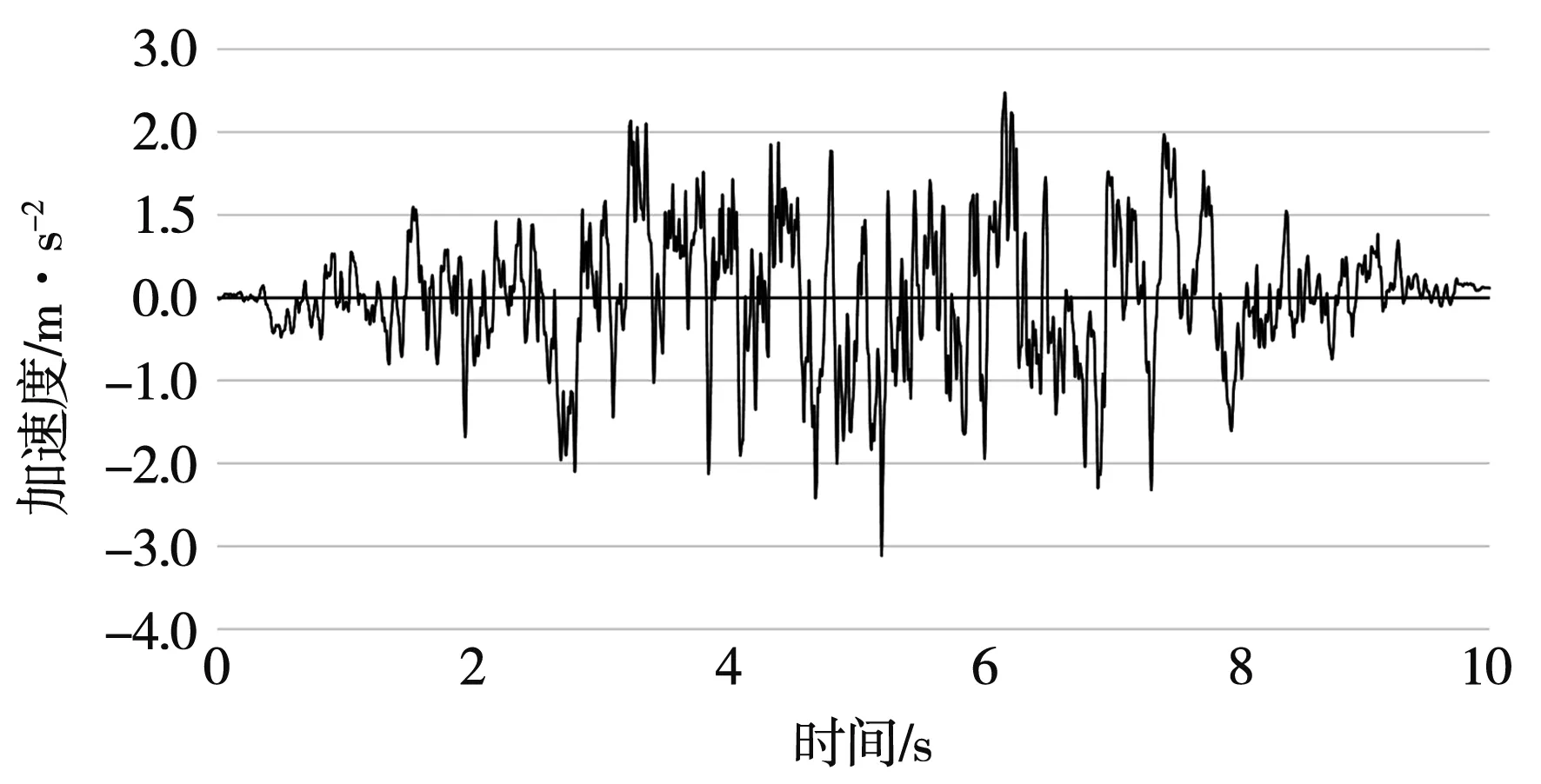
图4 顺河向地震波加速度时程曲线

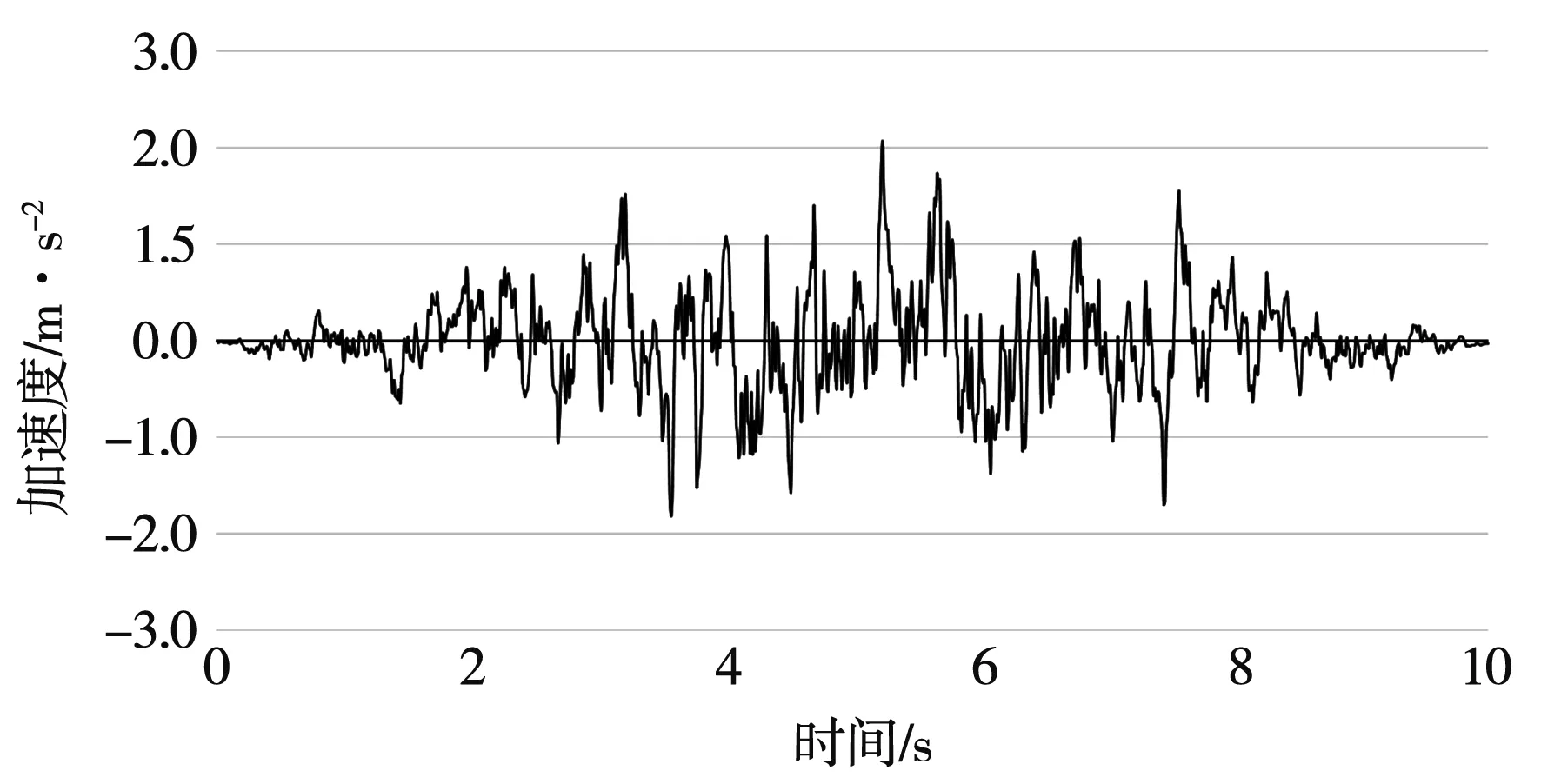
图5 竖向地震波加速度时程曲线

等效一致边界的地震动输入需要输入地震动速度和位移时程，由于加速度时程中长周期的存在，导致积分后的位移时程曲线出现漂移现象。这就需要对积分后的速度位移时程曲线进行基线校正，目前最小二乘法是采用较多的有效方法。以速度时程基线校正为例，见图6。

图6 速度时程曲线

3.3 计算结果分析

静态荷载主要考虑为自重+上游水压力+基地扬压力+泥沙压力，其中等效一致边界模型在地基边界截断处设置等效一致人工边界，地震动输入方式为基底等效荷载输入；无质量地基模型不设人工边界，地震动输入方式为沿基底输入地震动加速度时程。由图7可以看出，等效一致边界模型坝顶顺河向最大位移为1.95 cm，无质量地基模型坝顶最大顺河向位移为2.59 cm。与无质量地基模型相比，等效一致边界模型坝顶最大位移减小23.7%。

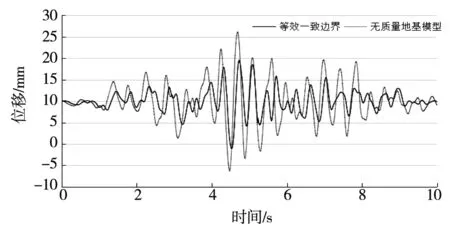
图7 坝顶顺河向位移

图8 两种模型坝踵主应力对比

比较两种不同模型时，考虑到人工边界地震波传播速度影响，与无质量地基地相比其峰值到达时间有明显的时间滞后，这段时间正是地震波从地基底部传播所耗的时间。等效一致边界模型位移有明显的滞后，其时间差值为地震波从坝底传播至坝基表面所消耗的时间。由图8可知，与无质量地基模型相比，等效一致边界模型第一、第三主应力分别减小37.5%和32.1%，这是由于无质量地基模型忽略了地基辐射阻尼的影响。

4 结 语

基于等效一致人工边界理论，利用有限元软件ANSYS平台，建立了坝体-库水-地基有限元模型。在模型地基边界截断处设置等效一致边界单元模拟地震波向无限远域地基逸散，并与传统无质量地基模型相比， 比较了两种模型坝体位移时程和坝踵应力，得出相关结论。本文实例应用表明，与传统无质量地基相比， 等效一致边界模型坝顶顺河向位移和坝踵应力均减小约20%～40%，这与目前对混凝土重力坝抗震分析的研究中，普遍认定的地基辐射阻尼效应对地震响应的影响可达20%～40%的结论相一致。本文研究成果可为同类工程抗震设计提供参考。