页岩油水平井压裂渗吸驱油数值模拟研究

欧阳伟平，张 冕，孙 虎，张云逸，池晓明

（1.中国石油集团川庆钻探工程有限公司长庆井下技术作业公司，陕西西安 710018；2.低渗透油气田勘探开发国家工程实验室，陕西西安 710018；3.中国石油集团川庆钻探工程有限公司，四川成都 610051）

页岩油储层致密，孔隙喉道小，毛细管力大，对水自发渗吸的作用较强[1]。在页岩油储层注水驱油受限的情况下，通过水力压裂充分发挥压裂液渗吸驱油作用显得尤为重要[2]。采用大规模水力压裂形成复杂裂缝网络，使页岩基质与裂缝中的压裂液充分接触，压裂液在毛细管力作用下渗吸至基质内，同时将基质中的油驱替至裂缝中，实现基质裂缝间油水置换，达到压裂液驱油效果[3]。与常规油气藏压裂相比，页岩油储层水力压裂除具有造缝作用外，还具有渗吸驱油和蓄能作用。压后闷井时间和压裂液用量是影响渗吸驱油和蓄能作用的关键参数，优化闷井时间和压裂液用量，能够提高页岩油储层压裂效果。

随着致密油气、页岩油气开发的不断深入，渗吸已成为油气藏工程研究的热点[4-9]。目前，主要进行了室内渗吸试验研究[10-18]，分析液体特性、岩石特性等因素对渗吸采出程度的影响。渗吸试验对于优选渗吸液具有指导作用，但是不能为压裂液用量、闷井时间等参数的设计提供指导，而压裂渗吸数值模拟是解决该问题的有效方法。国内外对渗吸油水置换的数值模拟的研究相对较少[19-23]，并且多为渗吸采油机理研究，无法直接应用研究成果和建立的模型优化页岩油压裂关键参数。

笔者以毛细管力为主要渗吸驱动力，基于体积压裂矩形裂缝网络，建立了一种考虑压裂液注入、闷井渗吸以及开井生产的压裂页岩油水平井油水两相渗流模型，利用控制体积有限元方法求解了该模型的数值解，模拟了渗吸作用下基质-裂缝油水置换的过程，获得了油水压力场、速度场、产量以及含水率的动态变化，分析了毛细管力、闷井时间、压裂液用量、基质渗透率以及缝网复杂程度对渗吸驱油的影响，可为页岩油水平井压裂优化设计提供理论依据。

1 物理模型

1.1 复杂缝网描述

水平井分段体积压裂后每段形成一改造区，其包含复杂裂缝网络，假定该改造区为矩形，含有主裂缝、次裂缝和支裂缝，主裂缝和次裂缝沿最大主应力方向延伸，主要为张开缝，支裂缝沿最小主应力方向延伸，主要为剪切缝，不同类型裂缝相互正交[24]，如图1 所示。每段存在1 条主裂缝，次裂缝的数量根据有效开启簇确定，支裂缝的数量由天然裂缝密度决定。主裂缝、次裂缝和支裂缝的导流能力不同，通常情况下主裂缝的导流能力最大，次裂缝次之，支裂缝最小。

图1 复杂裂缝网络描述示意[24]Fig.1 Description of complex fracture networks[24]

1.2 基质-裂缝相对渗透率曲线及毛细管力曲线

表征基质与裂缝油水相渗曲线的Corey 方程为：

基质的相渗相关系数根据实际岩心的测试结果确定，而裂缝由于渗透率很高，采用标准的裂缝相渗曲线，即束缚水饱和度Swr和Sor残余油饱和度均为0，幂律指数No和Nw均为1。裂缝渗透率很高，毛细管力很小，因此忽略裂缝毛细管力的影响。基质毛细管力与基质含水饱和度呈幂律关系：

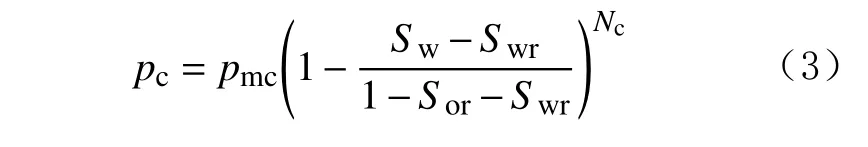
式中：Krw为水相相对渗透率；Kmw为水相最大相对渗透率；Sw为含水饱和度；Swr为束缚水饱和度；Sor为残余油饱和度；Nw为水相幂律指数；Kro为油相相对渗透率；Kmo为油相最大相对渗透率；No为油相幂律指数；pc为毛细管力，Pa；pmc为最大毛细管力，Pa；Nc为毛细管力幂律指数。

1.3 假设条件

1）原始储层均质有界，且渗透率具有各向同性，油藏存在油水两相，流动满足达西定律，油水黏度、压缩系数及体积系数随压力变化而变化，忽略储层的应力敏感效应和启动压力梯度效应。

2）水平井筒具有无限大导流能力，裂缝具有有限导流能力，流体在裂缝中的流动为一维流动，在基质中的流动为二维流动。

3）毛细管力为渗吸动力，忽略重力和温度变化对流动及渗吸作用的影响。

4）考虑压裂液注入、闷井渗吸及开井生产全过程，为了衡量压裂液蓄能效应，将压裂过程等效为压裂液注入至具有复杂缝网的储层中，引起压力及含水饱和度的上升，从而为模拟渗吸油水置换过程提供初始条件。

2 数学模型及求解

2.1 数学模型

式中：λ为流度，mD/（mPa·s）；p为压力，MPa；φ为有效孔隙度；Ct为综合压缩系数，1/MPa；Ctw为孔隙压缩系数与水压缩系数之和，1/MPa；Cto为孔隙压缩系数与油压缩系数之和，1/MPa；t为生产时间，h；Sw为含水饱和度；l为裂缝控制方程的坐标轴，m；wf为裂缝宽度，m；Γ表示边界；q为流量，m3/d；B为体积系数；h为储层有效厚度，m；下标o 表示油相，w 表示水相，c 表示毛细管力，m 表示基质，f 表示裂缝，i 表示初始值，I 表示注入，in 表示内边界，out 表示外边界。

2.2 模型求解

采用控制体积有限元法（CVFEM）求解上文的模型。控制体积有限元法是一种有限元和有限体积相结合的方法，采用有限元的插值函数和有限体积的数值计算格式，无需二次重建网格，可直接利用有限元网格，网格更灵活、精度更高，且具有有限体积局部守恒性特征，非常适合油藏油水两相流数值模拟。

基质压力控制方程中时间导数项的差分格式为：

基质饱和度控制方程中时间导数项的差分格式为：

裂缝压力控制方程中时间导数项的差分格式为：

裂缝饱和度控制方程中时间导数项的差分格式为：

利用非结构化网格离散技术对包含复杂网络裂缝的计算区域进行Delaunay 三角网格剖分，网格与裂缝网络完全匹配。连接三角形各边中点与三角形中心点，形成CVFE 网格，将裂缝与基质分开（见图2）。以单元节点为中心，对式（14）—（17）在CVFE 网格单元上积分，分别形成基质单元刚度矩阵和裂缝单元刚度矩阵，并根据单元节点信息，组成压力方程的总刚度矩阵及饱和度方程的总刚度矩阵，采用隐压显饱的方式迭代求解，详细的求解方法及步骤可参考文献[25]。

图2 裂缝基质的CVFE 网格示意Fig.2 CVFE meshes of the matrix and fractures

3 计算结果及分析

3.1 压裂渗吸驱油特征

假定储层初始压力为17 MPa，渗透率为0.1 mD，温度为65 ℃，有效厚度为10 m，孔隙度为10%，初始含水饱和度为0.45；水平井各压裂段的间距为60 m，井间距为400 m，因此单段控制面积为24 000 m2；单段多簇压裂液用量为857 m3，假定70%进入了目的层，即注入目的层液量为600 m3，有效开启3 簇，其中主裂缝1 条，次裂缝2 条，主次裂缝半长均为170 m，支裂缝10 条，缝长均为48 m，主裂缝导流能力为500 mD·m，次裂缝导流能力为200 mD·m，支裂缝导流能力为100 mD·m；压后闷井100 d 后按照先定产（单段产量4 m3/d）降压再定压（7 MPa）降产的方式生产。利用上文建立的油水两相渗流模型模拟不同毛细管力下单压裂段第1 年的生产动态，结果如图3和图4 所示。

由图3 可以看出，毛细管力越大，产油量越大，表明毛细管力渗吸作用具有明显的增产作用。此外，随着毛细管力增大，开井生产时的含水率及整个生产过程中的平均含水率都呈下降趋势。压后闷井过程中，在压裂液渗吸驱油作用下，裂缝中的水进入基质，置换出基质中的油，导致基质内含水饱和度升高，裂缝内含水饱和度降低，从而使开井生产时的含水率降低，在毛细管力足够大、闷井时间足够长的情况下，放喷排液阶段即可“见油”。

图3 单段在不同毛细管力作用下的产油量及含水率Fig.3 Oil production and water cut of single stage under different capillary forces

图4 为最大毛细管力3 MPa 下闷井75 d 时裂缝周围水相和油相的压力场及速度场（速度场箭头代表流动方向，箭头长度代表速度大小）。由图4 可以看出：裂缝内水相的压力大于基质水相的压力，水从裂缝流入基质（见图4（a））；基质油相的压力大于裂缝内油相的压力，油从基质流入裂缝（见图4（b））。由于基质与裂缝中的含水饱和度不同，引起毛细管力差异，形成渗吸驱动力，使基质与裂缝发生油水置换。从图4 还可以看出，主裂缝周围油水两相的流速较大，次裂缝及支裂缝附近油水两相的流速较小，远离裂缝区域油水两相的流速最小。此外，从油水相的压力场可看出，压裂液的注入能够大幅度提高储层压力，蓄能作用明显，该算例储层压力从初始的17 MPa 提高至开井生产时的31 MPa。

图4 闷井75 d 时裂缝周围油水相的压力场及速度场Fig.4 Pressure field and velocity field of the oil phase and water phase around the fractures on the 75th day of shut in

3.2 闷井时间优化

采用与3.1 节相同的储层参数，计算不同毛细管力条件下不同闷井时间单段第1 年的产油量，结果见图5。由图5 可以看出：对于无毛细管力的储层，储层内不存在渗吸作用，压后闷井产油量不能增加，因此对于常规中高渗透储层（毛细管力很小），是否闷井对产油量的影响非常小；对于具有毛细管力的储层，随着闷井时间增长，产油量升高，但升高幅度逐渐减小，且毛细管力越大，升高幅度减小的速度越快。这主要是因为毛细管力越大，渗吸作用越强，在基质渗透率不变的条件下，油水置换速度越快，最优闷井时间越短。假定以闷井1 d 单段产油量升高幅度大于0.15 t 为设计标准，优化设计闷井时间，该算例下最大毛细管力为1，2，3，4 和5 MPa时，最佳闷井时间分别为126，92，75，61 和56 d。

图5 闷井时间对单段产油量的影响Fig.5 Effect of shut-in time on the oil production of single stage

3.3 压裂液用量优化

注入压裂液达到一定量后缝网不再明显增加，因此假定缝网等其他参数不变，考虑压裂液用量对渗吸驱油和蓄能的影响，模拟计算最大毛细管力为3 MPa、注入不同量压裂液、闷井100 d 下单段第1 年的产油量和含水率，结果见图6。由图6 可以看出，随着压裂液用量增大，产油量和含水率均升高，但产油量的升高幅度逐渐减小，而含水率升高幅度逐渐增大。其原因在于，压裂液用量增大，导致基质与裂缝的含水饱和度差异增大，造成渗吸驱油压差增大，因此产油量升高，但是当注入压裂液的量超过了储层基质的渗吸能力，有些压裂液滞留在裂缝内无法进入基质，只能通过生产产出，造成含水率升高。算例中压裂液用量达到1 300 m3之后，含水率急剧升高，产油量升幅明显减小，因此该算例压裂液的最佳用量为1 300 m3。

图6 压裂液用量对产油量及含水率的影响Fig.6 Effect of fracturing fluid volume on oil production and water cut

3.4 基质渗透率的影响

模拟计算最大毛细管力为3 MPa、压裂液用量为1 300 m3时，不同基质渗透率单段第1 年产油量，结果见图7。由图7 可以看出，基质渗透率越高，产油量越高，最佳闷井时间越短，若按照同3.2 节相同的设计标准，基质渗透率为0.05，0.10 和0.30 mD 时，最优闷井时间分别为151，94 和45 d。其主要原因是毛细管力相同时，基质渗透率越高，油水流动的速度越快，基质与裂缝之间的油水置换速度也越快，最佳闷井时间也越短。

图7 基质渗透率对单段产油量的影响Fig.7 Effect of matrix permeability on the oil production of single stage

3.5 缝网复杂程度的影响

模拟计算有效压裂簇分别为1 簇、3 簇和5 簇时单段第1 年的产油量，结果见图8。1 簇无支裂缝，3 簇有10 条支裂缝，5 簇有14 条支裂缝，代表缝网复杂程度从低到高。由图8 可以看出，缝网复杂程度越高，产油量越高。其原因是：1）缝网越复杂，流动阻力越小，产油量越高；2）缝网越复杂，裂缝与基质间的渗吸面积越大，渗吸增油量越大。由于单簇裂缝与基质的接触面积太小，渗吸作用很弱，造成渗吸驱油量很低，如图8 中的红色虚线所示。对比3 簇和5 簇的产油量增幅可知，5 簇产油量增幅下降速度更快，其渗吸作用更强，最佳闷井时间更短，说明缝网复杂程度越高，渗吸面积越大，渗吸速度越快。

图8 缝网复杂程度对单段产油量的影响Fig.8 Effect of fracture network complexity on the oil production of single stage

4 结论

1）数值模拟结果表明：压后闷井阶段裂缝水相压力大于基质水相压力，水从裂缝流入基质，而裂缝油相压力小于基质油相压力，油从基质流入裂缝。基质与裂缝的含水饱和度不同，引起毛细管力，形成渗吸驱动力，使基质与裂缝发生油水置换。主裂缝周围油水相的流速均较大，次裂缝及支裂缝附近油水相的流速较小，远离裂缝区域油水相的流速均最小，说明油水置换主要发生在裂缝与基质的接触面。

2）毛细管力越大，最佳闷井时间越短，开井含水率和生产平均含水率越低，渗吸增产作用越明显；压裂液用量增大，不仅能提高储层压力，起到蓄能效果，还可使基质与裂缝的含水饱和度差异程度增大，渗吸驱油产量升高，但同时也会引起含水率升高，可通过含水率和产油量增幅优化压裂液用量。

3）最佳闷井时间主要受毛细管力、基质渗透率及缝网复杂程度的影响，其中毛细管力和基质渗透率决定油水置换的速度，而缝网复杂程度决定了油水置换的接触面积。毛细管力越大、基质渗透率越高、缝网越复杂，最佳闷井时间越短。

4）文中建立的渗吸油水两相渗流模型有助于提高压裂页岩油水平井产量的预测精度，同时可为优化页岩油水平井压裂液用量、闷井时间等关键参数提供依据。