北礵岛附近海域夏季海浪波高-周期分布特征

黄清泽，宋微，王庆业，陈晓禄，王恒，陈本清

（国家海洋局宁德海洋环境监测中心站，福建 宁德 352100）

1 引言

海浪是一种复杂的随机运动，海浪的生成和发展受风、水深和地理条件等多种因素影响，因此海浪特征和统计规律具有显著的地域特点。利用实测海浪资料，分析研究海域的波浪分布特征是十分必要的，对海浪理论研究和工程应用都有着重要的意义。

俞聿修等[1]采用渤海平台观测数据，给出了波高和周期分布、特征波要素以及频谱的关系。范顺庭等[2]利用黄河口海洋观测资料统计分析各波浪要素之间的特征比。束芳芳等[3-4]研究了广东阳西近岸测站1a实测波浪资料及该海域的谱型，认为双参数Weibull分布较适用于该海区的波高和周期分布规律，Longuet-Higgins改进分布和孙孚模式较适用该海区的波高和周期联合分布规律。李淑江等[5]分析了海南岛东南近岸海浪的季节变化和统计特征。陈剑桥等[6]利用浮标和岸基观测资料分析了台风“泰利”影响期间台湾海峡及周边海域的风浪特征。黄必桂等[7-8]根据南海实测波浪数据，研究了各特征波周期之间的关系，并给出了较适用于该海域的波高和周期联合分布。杨斌等[9]研究了杭州湾中部实测波浪数据，认为双参数Weibull分布能够较好地反映该海域波高和周期的分布规律。这些研究都通过不同海域实测波浪数据对波浪特征进行探讨，对理论分布函数进行验证和拟合，较准确地描述了研究海域的波浪特征。北礵岛位于台湾海峡西北部，该海域的波浪特征研究较少，本文根据实测波浪数据，对北礵岛附近海域海浪的波高和周期进行统计分析，讨论该海域的波高分布、波周期分布及波高和周期的联合分布特征，找到较符合该海域的波高分布、周期分布及波高与周期联合分布，为工程建设和防灾减灾提供参考和依据。

2 数据和方法

本文实测波浪数据观测地点位于福建省北礵岛附近海域，经纬度分别为120°22′E，26°42′N，水深28 m，时间跨度为2016年夏季（6—8月）。观测仪器为SBY1-1型波浪仪，以重力加速度方式测量海浪。其中，有效波高测量范围为0.2～25 m，测量准确度为±（0.1+5%H），H为实测波高；周期测量范围为2～30 s，测量准确度为±0.25 s。仪器每30 min观测一次，采样间隔0.25 s，每次连续观测约18 min，记录和输出4 096个数据供海浪分析。该海域夏季常受台风影响，本文所用实测资料也记录了2016年夏季台风影响下该海域的波浪变化过程，能够充分反映该海域夏季波浪特征。

通过对实测波面记录进行去中心化和消除趋势项处理，得到均值为零的波面数据，再删除一些显著异常数据，如在波峰或波谷处长达数秒长时间持续不变的波高记录，共获得可用波面记录4 396组。以此采用上跨零点法从实测波面记录中统计出海浪的最大波高（Hmax）、十分之一波高（H1/10）、有效波高（Hs）、平均波高（Hˉ）、均方根波高（Hrms）和平均周期（Tˉ）等海浪要素参数。

3 波浪要素统计分析

3.1 波高特征值统计

通过统计分析，2016年夏季（6—8月）观测海域有效波高变化范围为0.16～2.96 m，平均值为0.73 m，平均周期的平均值为4.50 s（见表1）。其中，除7月8日受台风“尼伯特”（1601）影响，有效波高达到最大值2.96 m外，海浪均以轻浪（0.5～1.2 m）为主，出现频率为62.60%，其次为小浪（＜0.5 m），出现频率为30.48%；有效波高＞2.5 m出现的频率为0.25%，出现在7月；平均周期均＞3 s，夏季平均周期主要出现在4～5 s之间，出现的频率为45.02 %，其次为3～4 s，出现的频率为32.32%（见表2）。

表1 观测期间有效波高和平均周期的变化范围和均值

表2 有效波高和平均周期分级统计出现频率（单位:%）

表3为实测波面数据统计得到的Hs、H1/10、Hrms与Hˉ以及Hmax、H1/10、Hrms与Hs之间的统计关系。应用最小二乘法，分别计算各特征波高之间的相关关系。其中，Hs、H1/10、Hrms与Hˉ的线性拟合系数分别为1.563、1.941和1.116，Hmax、H1/10、Hrms与Hs之间的线性拟合系数分别为1.599、1.244和0.712（见表3）。各特征波高之间的线性关系非常好，相关系数均大于0.98，线性拟合关系如图1所示。现将本文统计得到的特征波高比值系数同相应的Rayleigh分布理论值进行比较，由表3可知：实测的各特征波高比值系数在一定的范围内变化，各特征波高和有效波高的关系比各特征波高和平均波高的关系更稳定；由实测数据线性拟合得出的各特征波高与平均波高和有效波高的比值同Rayleigh分布理论值存在一定差异，普遍小于对应的理论值。

表3 特征波高比值系数

图1 各特征波高和平均波高以及有效波高之间的线性拟合

3.2 波高分布

Longuet-Higgins基于线性和窄谱的假定下，提出波高服从Rayleigh分布[10]，分布函数为：

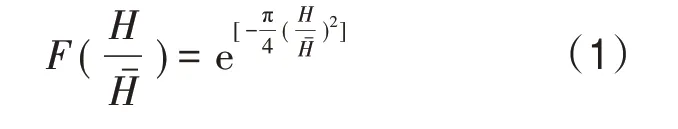
概率密度函数为：

波高的Rayleigh分布已经被广泛地应用[11]。该分布在水深较大且谱宽度较小的情况下，能够取得较好的结果，而对于大波的估计，理论结果较实际值偏大。Forristall[12]统计分析墨西哥湾8个测站116 h的飓风浪实测资料，认为相比Rayleigh分布，双参数Weibull分布更符合实际。不少学者采用双参数的Weibull分布来描述实际海浪波高分布，取得了较好的结果[13-14]。双参数Weibull分布的分布函数形式如下：

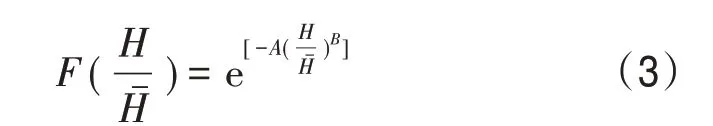
式中：A=；Γ(x)为伽马函数。

本文利用2016年夏季（6—8月）实测数据，首先将每组的波高以该组的平均波高做无因次化，以Δ=0.1为间隔，统计无因次波高不小于某一定值的概率（见图2黑色点），通过最小二乘法拟合出式（3）的系数，求得：A=0.771 2，B=2.139 2。因此，根据北礵岛附近海域实测波浪数据得到Weibull形式的波高分布函数为：

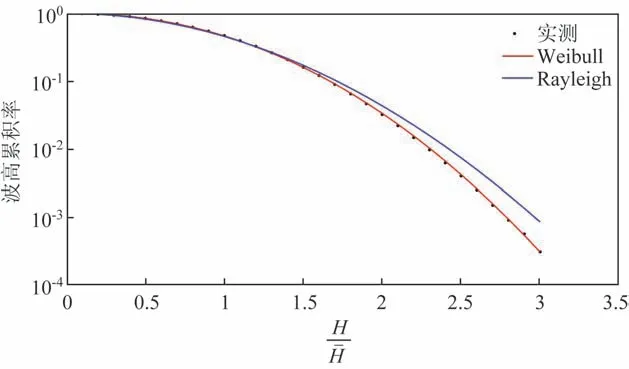
图2 实测与理论分布波高累积率

概率密度函数为：

利用K-C检验方法对式（4）进行检验。经过计算，实测结果和式（4）结果的最大绝对误差Dn=0.006 8，在组数为31且显著性水平d=0.05时，对应的临界值Dd=0.238 0，由于Dn＜Dd，故式（4）是可信的。图2为实测和理论分布的波高累积率。从图中可以看出，Weibull分布计算出来的结果能够较好地符合实测结果，而Rayleigh分布给出的波高累积率相对实际值偏大，并且随着的增大，这种差异更加明显。将式（1）和式（4）分别变换为：

式（6）和式（7）计算结果和实测值对比如表4所示。由表4可知，Weibull分布计算结果较符合实测结果，而Rayleigh分布计算的结果与实测结果差别较大，尤其是小概率波高，Rayleigh分布计算结果大于实测结果。

表4 无因次波高（H ）的计算值与实测值对比

表4 无因次波高（H ）的计算值与实测值对比

项目实测值Weibull Rayleigh F/%0.01 3.24 3.19 3.42 0.1 2.78 2.79 2.97 1 2.29 2.31 2.42 2 2.12 2.14 2.23 5 1.88 1.89 1.95 10 1.66 1.67 1.71 20 1.41 1.41 1.43 30 1.24 1.23 1.24 40 1.09 1.08 1.08 50 0.96 0.95 0.94 60 0.83 0.82 0.81 70 0.70 0.70 0.67 80 0.56 0.56 0.53 90 0.38 0.39 0.37

利用式（5）计算得到当波高概率密度最大时(H/)max=0.841 1，这意味着在北礵岛附近海域波高分布中，出现最大概率密度的波高是平均波高的0.841 1倍，略小于平均波高的波占优势，根据式（2）计算得到的波高最大概率值对应的无因次波高(H/)max=0.8。因此，本文拟合的Weibull公式得到的最大概率密度波高比按Rayleigh分布求得的约大5%。图3为北礵岛附近海域实测海浪波高分布的概率直方图及Rayleigh分布和Weibull分布概率密度曲线。由图3可知，北礵岛附近海域实测波高呈不对称性分布；Rayleigh分布在平均波高附近的概率密度值比实测偏低，对于＞1.8时Rayleigh分布给出的概率值大于实际分布；此外，利用2016年9月实测波浪数据对给出的Weibull分布进行检验，结果如图4所示，Rayleigh分布理论值和Weibull分布理论值与实测波高累计率的均方根误差分别为0.012 9和0.004 4。与Rayleigh分布相比，本文拟合的公式给出的结果和实测波高分布吻合较好。

图3 实测海浪波高分布与理论分布比较

图4 9月Weibull分布和Rayleigh分布与实测波高累积率对比

3.3 周期分布

很多学者对周期的理论分布进行了大量研究，Longuet-Higgins基于线性和窄谱的假定，提出了与谱宽参量有关的周期分布的理论形式[15]。根据线性海浪模式及波动的射线理论，孙孚[16]提出周期和波高的联合分布（简称“孙氏分布”），对波高进行积分也可求出周期密度函数。然而，周期的理论分布形式涉及谱宽参量，计算复杂，因此在实际中经常采用半经验的周期分布形式。Bretschneider[17]根据观测资料提出的周期分布函数为：

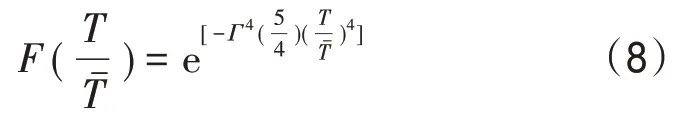
概率密度函数为：

对于式（8），不少学者认为指数部分取值应比4小，也有学者认为Bretschneider周期分布是Weibull分布的特殊形式，宜采用Weibull分布拟合海浪周期分布，根据实测波浪数据，求出周期Weibull分布中的参数[13-14]。根据本文的实测波浪数据，将每组的周期以该组的平均周期做无因次化，得到Weibull形式的海浪周期分布函数为：

概率密度函数为：

同样使用K-C检验方法对式（10）进行检验。经过计算，实测结果和式（10）结果的最大绝对误差Dn=0.028 4，在 组数为31且显著 性水平d=0.05时，对应的临界值Dd=0.238 0，由于Dn＜Dd，故式（10）是可信的。图5为实测海浪周期分布概率直方图及理论概率密度曲线。从图中可以看出，绝大部分周期出现在两倍平均周期范围内，实测周期分布主要集中在平均周期附近；Bretschneider的周期分布表现出在平均周期附近的概率值过高，对于较小和较大周期波高概率密度预测值过低；本文给出的周期分布和实测周期分布符合较好。根据式（11）求出周期的最大概率值为=0.931 7，这表明波群中出现的可能最大周期接近于平均周期。

图5 实测海浪周期分布和理论分布比较

3.4 波高和周期联合分布

海浪波高和周期的联合分布的研究已经取得了很大的进展，1975年Longuet-Higgins首先基于线性和窄谱假设[15]，提出了波高与周期联合分布，其概率密度函数为：

波高和周期的联合分布是不对称的，Longuet-Higgins通过引入归一化因子L(ν)，对式（12）进行改进，得到波高和周期非对称性联合分布[18]：

孙孚[16]根据线性海浪模式及波动射线理论，提出的波高与周期联合分布模型，其概率密度函数为：

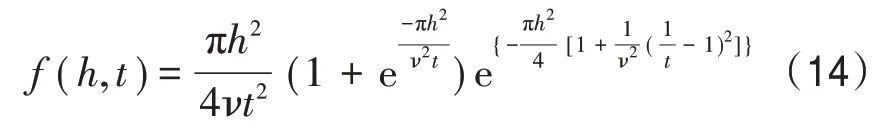
将本文的实测波高和周期分别以平均波高和平均周期做无因次化处理，区间间隔=0.1，统计求出波浪在各区间的概率密度。将式（12）、式（13）和式（14）进行对比，结果见图6。由图6可知，实测波高和周期联合分布接近斜三角形，具有明显的不对称性，高概率发生区域（概率密度＞0.8）大致在无因次周期0.3～1.1，无因次波高0.1～1.1；在3种理论分布中，Longuet-Higgins分布外观表现为明显的正三角形，与实测结果不相符，Longuet-Higgins改进分布和孙氏分布外观类似，但和实测分布仍存在着差异，实测分布的高概率区域范围大于Longuet-Higgins改进分布和孙氏分布的高概率区域，且相对右偏，对于大波高大周期的波和小波高小周期的波出现的概率，实测结果大于理论值，其原因可能在于理论分布基于窄谱假设，而北礵岛附近海域夏季海浪受到涌浪的影响多，谱宽度较大，平均值为0.53，因而存在误差。

图6 波高与周期联合分布

4 结论

根据北礵岛附近海域2016年夏季（6—8月）的实测波浪资料，分析了北礵岛附近海域波浪的统计特征，讨论了该海域波高分布、周期分布与波高和周期的联合分布，主要结论如下：

（1）观测海域海浪以轻浪和小浪为主，有效波高的平均值为0.73 m，最大值为2.96 m，平均周期的平均值为4.50 s。

（2）通过对实测波高特征值的统计分析，各特征波高与平均波高和有效波高之间的线性关系，普遍小于对应的Rayleigh分布理论值。

（3）根据对北礵岛附近海域实测波高和周期的统计分析，双参数Weibull分布对研究海域的波高分布和周期分布吻合的较好。Longuet-Higgins改进分布和孙氏分布在广西阳西近岸海域[3]和江苏北部辐射沙洲南部沿海[19]中能够较好地符合实际，而根据本文实测波高和周期的联合分布与各理论分布的对比，Longuet-Higgins改进分布和孙氏分布也能够推广到北礵岛附近海域的波高和周期联合分布特征中。