基于机器学习的海表温度对中国降水的预测研究

李良伟，邹斌，石立坚，刘鹏

（1.国家卫星海洋应用中心，北京 100081；2.国家海洋环境预报中心，北京 100081；3.自然资源部空间海洋遥感与应用重点实验室，北京 100081；4.南方海洋科学与工程广东省实验室，广东 广州 511458）

1 引言

海表温度（Sea Surface Temperature，SST）与降雨有着密不可分的联系，以往的一些研究集中在降水与局部和区域尺度SST变化关系上。Zahraie等[1]利用K-means聚类算法和遗传算法（Genetic Algorithm，GA），将阿曼湾、阿拉伯海和印度洋北部选定区域的SST进行聚类，提出了改进的K-means方法和GA模型，该模型可以有效地用于研究区域正常降水的季节预测，这两种聚类技术的结果已被用于制定伊朗东南部省份的季节性降水预测指南中。Cordery等[2]观察到一个季节的全球和局部现象与干旱事件的未来4个季节的降水之间有着很强的关系，例如太平洋SST异常可用于预测澳大利亚东部的低降水季节。Higgins等[3]利用热带太平洋SST对Nino-3.4地区的气温和降水作出了客观的季节预报，并且跟踪并比较了这些预测与8 a的观测结果以及美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration，NOAA）官方发布的美国气候预测中心（Climate Prediction Center，CPC）的季节性预报结果的差异。不同时间尺度的SST和海温大气耦合系统的震荡通常会对降雨活动产生重要的影响。对中国降水有影响的包括：季节或年内震荡，主要是受太阳辐射周期的变化，时间尺度通常为1 a，如季风；年际震荡，如厄尔尼诺与南方涛动（El Niño-Southern Oscillation，ENSO）[4]；年代际震荡，如太平洋年代际振荡（Pacific Decadal Oscillation，PDO）[5]，这些震荡在降水长期预测以及气候预测中有重要作用。研究指出，ENSO循环对中国降水具有很大影响[6-7]。陶诗言等[7]研究发现ENSO的不同阶段对中国夏季降水有不同的影响。王绍武等[8]利用近500 a旱涝资料，指出赤道中太平洋地区年代际变化与中国东部36 a旱涝周期关系密切，从而提出了与海气相互作用有关的旱涝36 a周期变化机制。于淑秋等[9]应用滑动T检验法对北太平洋海温年代际跃变进行了研究，指出在1976/1977年SST跃变前中国汛期降水量在东北地区偏少，华北地区偏多，长江流域偏少，华南偏多，而跃变后则相反。朱益民等[10]指出，PDO位于暖位相期（即中纬度北太平洋异常冷，热带中东太平洋异常暖），冬季阿留申低压增强，蒙古高压也增强（但东西伯利亚高压减弱），中国东北、华北、江淮以及长江流域大部分地区降水偏少。针对具体海域对降水的影响，孙柏民等[11]指出，夏季江淮流域降水与1月黑潮区的SST有很好的正相关关系，与6月SST则呈负相关。

中国降水的主要因素有来自印度洋和太平洋受SST驱动的季风和台风，也有受不同时间尺度的SST和海温大气耦合系统的震荡（如ENSO和PDO等）的影响，过去大多数研究都是以某一具体海域的温度异常或者局部海域的海气耦合震荡来研究对中国降水的影响。本文则以30°E～70°W和50°N～50°S的SST为研究范围，这也是影响中国降水的季风、台风以及黑潮的主要来源及活动海域。通过机器学习的方法来挖掘SST对中国降水的时空影响，利用聚焦时延神经网络（Focused Time-Delay Neural Network，FTDNN）尝试利用SST对聚类后的中国降水进行中长期的预测。

本文探索通过机器学习的方法建立SST与周降水量的机器学习模型，并用此模型预测各聚类区的周降水量。通过预测的周降水量累加可得到月降水量或季度降水量，从而预测出该区域降水量较长一段时间内的趋势变化。

2 数据

本文所用的两个数据集如下：

中国日降水量取自中国地面降水日值0.5°×0.5°格点数据集（V2.0）。该数据集是基于国家气象信息中心基础资料专项最新整编的中国地面高密度台站（2 472个国家级气象观测站）的降水资料，利用ANUSPLIN软件的薄盘样条法（Thin Plate Spline，TPS）进行空间插值，生成1961年至最新的中国地面水平分辨率0.5°×0.5°的日值降水格点数据。

SST取自NOAA最优插值（Optimal Interpolation，OI）SST每周数据；时间为1981年10月29日—2016年11月13日；SST的选取范围为30°E～70°W和50°N～50°S，这是影响中国降水的季风、台风以及黑潮的主要来源及活动海域。

3 研究方法

3.1 降水的时间序列聚类

时间序列是由一组按时间先后顺序排列的变量组成，它通常是在相等间隔的时间段内，依照给定的采样率，对某种观测要素进行长期观测得到的[12]。本文将使用K-means聚类算法，选取时间序列的相关性特征将时空立方体的位置划分为多个簇，每个簇内的时间序列的相关性值较为接近，彼此之间的相似程度高于其他簇中的时间序列[13]。在时间范围内，统计相关性来衡量时间序列的相似性时，例如，时间序列（1，2，3，4，5）与时间序列（10，20，30，40，50）的值不同，但是完全相关，其差为0，可以通过1减去相关性来计算两个时间序列之间的差。这意味着完全正相关（相关性=1）的时间序列的差为0，不相关（相关性=0）的时间序列的差为1，而完全负相关（相关性=-1）的时间序列的差为2。所有其他相关程度将生成介于0～2之间的值，正相关性越大表明相似度越高。

本文使用轮廓系数（Silhouette）法确定降水的最佳聚类数。Silhouette系数由Rousseeuw[14]于1987年提出，它能够衡量一个结点与它属聚类相较于其他聚类的相似程度，计算方法如下：

式中：a(i)为样本i到同簇其他样本的平均距离，a(i)称为样本i的簇内不相似度，簇C中所有样本的a(i)均值称为簇C的簇不相似度；b(i)为样本i的簇间不相似度，b(i)值越大，说明样本i越不属于其他簇；s(i)接近1，则说明样本i聚类合理；s(i)接近-1，则说明样本i更应该分类到另外的簇；若s(i)近似为0，则说明样本i在两个簇的边界上。

3.2 主成分分析降维

主 成 分 分 析（Principal Component Analysis，PCA）可以用于减少特征空间维数、选择最有用的变量、确定变量的线性组合和识别目标或是异常值分组等[15]。对于一组数据中某个特征组成的多维向量，其中的某些元素本身没有区分性，比如都为0，或者与0相差很小，那么这个元素本身就没有区分性，用它做特征来区分，贡献会非常小。我们的目标是找到变化大的元素，即方差大的那些维，去除掉变化不大的维，从而使特征留下的都是最能代表此元素的值。例如，本文中对于SST在99%的方差被保留之后，SST的数据维度从20 000多个降到600多个。方差太少时无法代表所有的海温活动，而过大时，会大幅增加输入神经网络的维度，增大神经网络的训练时间，最终的预测结果也不理想。本文经过测试最终保留了SST均方差为91%的维度来研究主要维度对降水的影响。表1与图1是本文输入神经网络中的前6个主要维度的方差和空间模态。第一模态代表了SST的季节性模态，后5个模态在赤道和太平洋显示出很大的变化，这些模态捕获了ENSO、PDO和北太平洋环流振荡（North Pacific Gyre Oscillation，NPGO）等现象[16]。

表1 前6个主要维度的方差

图1 SST前6个主要模态的空间分布

3.3 FTDNN

时延神经网络（Ti me-Delay Neural Network，TDNN）是一种多层人工神经网络结构，由Waibel等[17]于1989年提出。初衷是为了解决语音识别中，传统方法隐马尔科夫模型（Hidden Markov Model，HMM）无法适应语音信号中的动态时域变化。该结构参数较少，进行语音识别不需要预先将音标与音频在时间线上进行对齐，实验证明TDNN比HMM表现更好。TDNN的提出具有非常重要的影响，卷积神经网络（Convolutional Neural Networks，CNN）就是受TDNN影响而发明的，它是卷积网络的前身。FTDNN神经网络可以看作是一维的卷积神经网络，它的共享权重被限制在单一的维度上，且没有池化层，通过共享权值可以方便学习，在学习过程中不要求对所学的标记进行精确的时间定位，且有能力表达语音特征在时间上的关系，非常适用于语音和时间序列的信号处理[18]。

TDNN与其他神经网络一样，由多个由簇组成的互连层进行操作。这些集群意在表示大脑中的神经元，像大脑一样，每个集群只需要注意输入的小区域。原典型TDNN具有3层集群，一组用于输入，一组用于输出，中间层通过过滤器处理输入的操作。由于它们的顺序性质，TDNN被实现为前馈神经网络。在TDNN前馈网络的输入端带一个抽头延迟线，称为FTDNN。这是动态网络的一部分，称为聚焦网络，其中动态只出现在静态多层前馈网络的输入层。该网络非常适合时间序列预测，例如混沌激光的测量数据集，该数据集是圣达菲时间序列竞赛中使用的数据集，使用FTDNN网络显示出很好的预测效果[19]。FTDNN网络的优点之一是它不需要通过动态反向传播来计算网络梯度，这是因为抽头延迟线只出现在网络的输入端，不包含反馈回路或可调参数，因此该网络比其他动态网络的训练速度更快。

本文将日降水数据处理为周降水数据，使之和NOAA的SST产品数据的时间一致，经过K-means聚类得到最佳的聚类结果之后，再将各区域的格点数据取平均。由于降水数据是周数据，原始数据存在一些较大的异常值（见图2），而异常值的存在会极大地干扰模型训练，必须对原始数据进行平滑处理。常见的平滑方法有移动平均法、加权平均法和指数平滑法。移动平均法虽然可以很好地过滤掉异常值，但是平滑后的时间序列过于平稳，造成每个分类之间的差异不够明显，而加权平均法中合理地分配加权系数较为困难。通常我们认为每周的降水不是一个孤立事件，它不会突然地增大，比如台风对某地降水的影响。事实上在台风来临前的一段时间内，它所影响的区域的降水就会增加，在登陆时增大更加明显，基于此最后选择指数平滑算法对原始数据进行平滑。如图2所示，平滑后的结果降低了异常值的大小，但同时也保留了原始周数据的波动性。

图2 降水周数据以及平滑后的降水数据

4 结果与讨论

4.1 最佳聚类数的确定

基于相关性聚类的轮廓系数值如图3所示。随着簇数的增加轮廓系数值也增加，但增长速度放缓，聚类数为7时，轮廓系数值最大。通常轮廓系数值越大聚类效果越好，但聚类数太大时海洋对陆地降水的影响就会分散，聚类数太少时，会使地理空间跨度太大，每个分类的平均值不能很好地代表所包含的时间序列的特征，本文最终选取轮廓系数值最大的7为最终的聚类结果。图4为基于相关性分7类的聚类结果。从地理分布来看：区域1主要包括东北和内蒙古北部地区，区域2大部分属于华北和西北东部区域，区域3则属于西北地区，区域4大部分属于青藏高原区域，区域5大部分属于西南区域，区域6大部分属于长江以南的华东、华中和华南区域，区域7属于黄河和长江之间的华中和华东区域。从气候区分布来看，区域1、区域2、区域5、区域6和区域7大部分处于季风区，其降水受季风、台风和ENSO等海洋活动的影响较大，而区域3与区域4大部分属于温带大陆性气候和高原山地气候。本文所分的7个区域分布与中国年降水量分布以及传统的中国气候区分布有所差别，这与本文所用的数据是周降水量波动比较大有关，而传统气候区在划分时除了结合气候区划分外，还要结合生产实际需要并适当照顾自然区或行政区[20]。

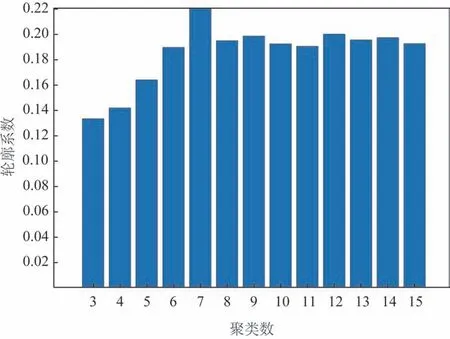
图3 基于相关性的轮廓系数值

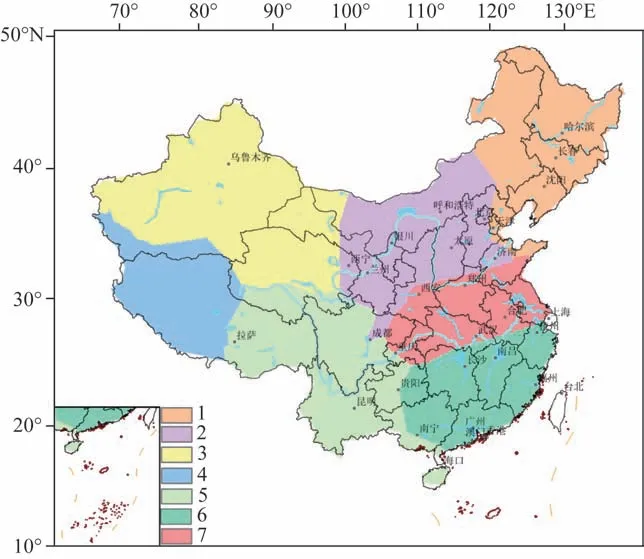
图4 基于相关性分7类的聚类结果

4.2 聚类特征的可视化

由于降水周数据的数据量比较大，时间序列过长会造成可视化后的数据分布较密集，而每一个簇内包含上百个时间序列，都将其可视化的结果并不理想。为了更好地展示聚类效果和每一个簇的特征分布，选取时间为1993—1998年，空间上使用随机函数随机选取5个点的时间序列。

图5a—c表明相同簇的降水时间序列具有类似的特征，而图5d与图6表明不同簇的数据分布有明显的差别。同一簇具有相同性，而不同簇具有很明显的差异性，说明聚类结果较为理想。

图5 分7类时的降水随时间的变化

图6 分7类的降水散点图和小提琴图

4.3 各区域分析

各区域以训练集、验证集和测试集的比例为8∶1∶1输入数据，通过FTDNN进行训练，结果如表2所示。随着运行次数的增加，各区域测试集的最小均方根误差、相关系数以及全集的最小均方根误差的最佳延迟时间都稳定在相同的延迟时间。图7是各区域测试集的平均绝对误差，从图7中可以看出，区域1、区域2、区域5、区域6和区域7的平均绝对误差大于另外两个区域，这是因为这5个区域的降水主要受季风、台风和ENSO等海洋活动影响，从而造成周降水值的波动较大。从表2可知，区域1的最佳延迟时间为3周，区域2为4周，区域3为2周，区域4为2周，区域5为5周，区域6为6周，区域7为4周。可见，区域1、区域2、区域5、区域6和区域7等处于季风区区域的最佳延迟时间都比另外两个处于非季风区的最佳延迟时间大，这可能是由于本文所使用数据的时间分辨率为周，季风区受季风和台风带来的降水量比较大导致的。在得到各区域的最佳延迟周后，输入确定的延迟时间，对各区域单独进行训练，图8与表3是使用各区域训练得到的模型对各区域2012年7月1日之后11周降水的预测情况。区域6与区域7的预测误差较大是因为2012年区域7受到台风带来的降水的影响，导致该区域降水波动比较大，而对波动较大的信号，通常很难预测准确，区域3与区域4则显示出很好的预测效果。

图7 测试集的平均绝对误差

表2 各区域训练结果

图8 2012年7月1日之后11周各区域的预测情况

表3 连续11周的各区域模型预测的评价指标

在降水量的中长期趋势分析上，通过预测的周降水量累加可得月降水量，从而刻画出该区域降水量较长一段时间内的趋势变化。这里我们给出了区域6的预测结果。从图9可知，在大约7.3 a的降水量预测中，月降水量的预测值与真实值的相关系数达0.92，均方根误差为3.81，较准确地预测了真实降水量的趋势变化，其他区域的预测情况见表4。与传统的小波变换重建原序列以及均生函数方法的预测结果相比[22]，本文预测结果的相关系数和均方根误差都有了很大的提高，例如在新疆地区本文测试结果的相关系数比小波变换结果提高了0.05。

表4 各区域连续88周趋势预测的评价指标

图9 区域6连续88 M的预测值与真实值趋势及相关性

5 结论

本文利用机器学习的方法，以30°E～70°W和50°N～50°S的SST为研究对象，通过K-means聚类算法将36 a的中国周降水数据聚为7个区域，其中区域1、区域2、区域5、区域6和区域7的大部分区域处于季风区，而区域3与区域4的大部分区域属于温带大陆性气候和高原山地气候等非季风区。将各区域降水数据经过指数平滑之后输入FTDNN，并求解其与经过降维处理的SST之间的关系。结果表明，区域1、区域2、区域5、区域6和区域7等受季风和台风等海洋活动影响较大的区域的最佳延迟时间比远离海洋区域的最佳延迟时间大，同时也得到了预测各区域降水的最佳延迟时间，其中区域1的最佳延迟时间为3周，区域2为4周，区域3为2周，区域4为2周，区域5为5周，区域6为6周，区域7为4周。在对各区域进行连续11 a的预测中得出，FTDNN神经网络在利用降维后的SST来预测降水量上显示出很好的预测效果。

在中长期趋势预测上，本文的方法也可较准确地预测出某一区域未来降水量的趋势变化，相比传统方法预测能力有了较大的提高。但在受海洋活动影响较大区域，短期预测的降水会有很多局部突变值，预测结果不理想，这也是非线性和非平稳信号预测中的难点，以后我们将尝试将FTDNN结合集合经验模分解来提高预测效果。