基于ARIMA和LSTM的城市轨道交通延时客流预测方法比较

李德奎，杜书波，张 鹏

(1.聊城大学 a.计算机学院；b.建筑工程学院，聊城 252000；2.同济大学 建筑与城市规划学院，上海 200092；3.西悉尼大学 建筑环境学院，悉尼 NSW2751)

近年来，为提升公共服务水平、提振夜间经济及满足城市居民夜间出行的需求，北上广深等一线城市的轨道交通的运营时间在不断延长。上海市从2017年4月1日起，常态周末(周五、周六)以及节假日的最后一个工作日延长运营1 h，部分城市有夏季或是周末常态、节假日延长运营的策略。在运营精细化的背景下，如何在延时运营的同时平衡能耗、运营和居民需求之间的关系，延时时长及线路选择能否更加精确合理，能否制定符合居民需求的弹性延时制度，是城市管理者以及城市轨道管理者所面临的挑战。

本文利用上海轨道交通刷卡数据，利用时间序列数据分析中最为有效的ARIMA和LSTM模型对轨道交通延时客流进行预测，同时对比了不同时间粒度以及不同数据选取量下的两种预测方法的优劣性，为轨道交通运营决策提供科学的依据及理论支持。

1 城市轨道交通延时与客流预测研究

1.1 城市轨道交通延时研究

随着居民出行以及城市低碳运营的整体需求，我国城市轨道交通急速发展，更多城市开始进入平稳发展期，改善服务质量、提高运营效率是这一时期的主要目标。运营时长是提高服务质量的一个重要考量指标，但运营时长会降低整体运营效率，增加能耗和成本，如何平衡服务质量与运营效率间关系，这是城市管理者以及轨道交通运营者关注的问题。

城轨交通运营时长与气候、市民生活习惯等诸多社会因素相关，但是这些因素难被量化，难与运营时长进行相关性研究。但是延长轨道交通运营时长对公共服务的完整性和均质化有很大的影响，可以改善交通服务的质量，给夜间工作人群以及夜间经济活跃区域提供更便捷的交通工具选择。从另一个角度来说，轨道交通的延时运营可以培育和改变人们的出行方式，使人们的日常生活和轨道交通出行方式深度结合，特别是改变夜间出行方式，这样可以拉动城市的夜间经济，同时夜间经济也将拉动人们的夜间出行需求，这是一个互相促进的过程[1]。

1.2 城市轨道交通客流预测研究

轨道交通的客流预测分为长期预测以及短期预测，长期预测主要针对城市的发展对交通需求的变化而进行的基于城市人口密度、流动性等进行的预测。短期预测是在轨道交通运营后，以周或天为单位的预测。轨道交通短期客流预测为客运组织安排提供可靠支撑，并且能有效降低拥堵和提高整个轨道交通线网的管理和服务能力[2]。

国内外学者对短期客流预测方法进行大量的研究，大部分研究都基于时间序列分析算法。按照数据来源主要分两种，一种是利用客流数据自身客流变化进行预测的单变量预测研究，一种是通过外部数据(天气、气候、节日等)对短期客流数据进行的多变量预测研究。

在单变量预测研究中，由于轨道交通的数据序列之间有相互依赖关系，因此采用自回归移动平均模型(ARIMA)来进行研究的较多。卢志义等通过ARIMA模型对天津一号线2个月的数据进行了拟合和预测，得出地铁客流数据具有平稳性，适合使用ARIMA模型进行建模和拟合的结论[3]。蔡昌俊等通过ARIMA模型对广州地铁2号线2011年至2013年的客流量进行了拟合以及预测，得出了使用ARIMA对进出站客流进行预测的适用性较高的结论[4]。随着深度学习的算法普及，使用深度学习算法进行轨道交通客流预测的研究也开始广泛出现。龙小强等结合深度信念网络(DBN)和支持向量机(SVM)提出了DBN-P/GSVM模型，通过对成都地铁2016年3月的客流量周一到周五的客流进行预测，并和长短期记忆网络(LSTM)算法进行了比较[5]。XIONG等也对比了LSTM和CNN算法，对北京市地铁数据进行了预测分析并对算法进行了比较[6]。

在多变量预测研究中，主要集中在外部天气因素的研究中。李梅等通过结合外部天气数据，综合考虑影响地铁站客流的内外部因素，提取了包括天气数据在内的12个显著影响因子，对上海轨道交通莘庄站的短期客流进行了LSTM模型预测[7]，取得了较好的拟合度。崔洪涛等对轨道交通客流量数据、节假日数据和气象数据进行了融合，并比较了不同模型的精度[8]。LIU等结合天气数据提出了基于LSTM的DeepPF算法，对南京地铁的客流数据进行了分析[9]。HAO等结合天气数据等外部数据主要比较了LSTM算法和seq2seq算法对新加坡地铁客流的影响[10]。

虽然近年来对地铁客流预测的研究很多，但是没有专门对地铁延时的客流预测进行的研究，而且很多使用深度学习算法的研究虽然都加入了ARIMA算法进行了比较，但是没有专门对ARIMA算法和其他算法进行详细分析[10]。因此本文集中在比较作为传统算法中较流行的ARIMA和深度学习算法中较流行的LSTM算法的有效性和精度上。

2 轨道交通数据特点

城市轨道交通的线路固定，居民使用轨道交通时带有很强的时间周期性，受外界因素干扰较小，整体轨道交通客流量的数据带有时序性的特点，即客流量会随着时间的变化而变化，根据季节、月份不同会有一定的变化周期，但是最基本的变化周期是以周为单位的变化，通常周一到周五白天会有一个变化周期，周五晚到周日白天会有一个变化趋势，周日晚是一个趋势[5,9-10]。

由于本文是对轨道交通延时后的客流进行预测，因此针对的是客流数据一天内的特征进行分析，数据来源于上海市轨道交通提供的公开数据，提取了其中的无特殊特征的一天数据作为研究对象，分析这一天内的数据变化情况。具体时间为2015年4月13日周一，总数据量为8 893 497条，在时序数据分析中，不同的时间间隔会出现不同的变化[5]，因此本文将数据分成5 min间隔和15 min间隔进行汇总后单独进行分析处理，使用不同的数据分析方法来比较方法的精度。

客流量在一天内的变化特征如图1和图2所示，不管是5 min间隔还是15 min间隔，都出现了明显的早高峰和晚高峰特点。但是在15 min间隔(图1)中，数据变化比较平缓，5 min间隔(图2)数据波动比较大，引起这种变化的原因主要是地铁的运营时间主要以5～10 min为主，将数据粒度变小会更加体现客流的波动情况。

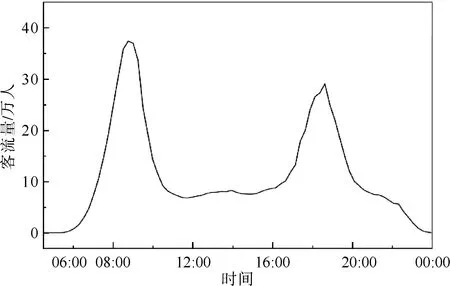
图1 15 min间隔客流变化

图2 5 min间隔客流变化

3 AMRIA和LSTM机理以及流程

3.1 ARIMA

时间序列数据是按照时间顺序排列的、随时间的变化而变化，相互关联或是不关联的数据序列，可以通过曲线拟合和参数估计来建立数学模型进行预测的理论和方法，称为时间序列分析，主要的分析方法有简单移动平均法、加权移动平均法、趋势移动平均法、一次指数平滑法、二次指数平滑法和ARIMA(Autoregressive Integrated Moving Average Model，自回归移动平均模型)。

ARIMA模型是指将非平稳时间序列转化为平稳时间序列，该模型的核心是将预测对象随时间的变化而形成的序列认为是一个随机序列，因此可以用模型来近似描述以及预测这个序列。基于ARIMA模型或组合模型具有较好的适用性和较高的预测精度，其在交通、建筑、生物、金融等行业应用广泛。ARIMA的建模思想是通过若干次差分化非平稳序列为平稳序列，即通过d次差分，对平稳序列建模后再反变换得到原序列[3]。严格来说，ARIMA模型并不是一个特定的模型，而是一类模型的总称。通常用p，d，q值来确定，记做ARIMA(p，d，q)，由移动平均模型MA，自回归模型AR和差分模型Difference组成，其构成如式(1)所示：

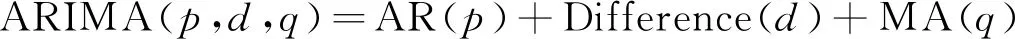
(1)

式中：q为移动平均模型的阶数；p为自回归模型阶数；d为差分阶数。

ARIMA模型的关键是对p，d和q的定阶。ARIMA模型的数学式为式(2)：

(2)

式中：yt为t时点的预测值；μ为常数项；p为自回归模型阶数；q为移动平均模型的阶数；εt为整体误差值；γi为i阶自回归系数；yt-i为t-i阶预测值；φi为i阶移动平均系数；εt-i为t-i阶误差。

ARIMA的建模步骤如图3所示。首先对时间序列数据进行平稳性检测，若不通过，则采取差分变换将其变为平稳序列。通过平稳性检测之后，进行白噪声检测，当序列不是白噪声序列时，即可选择合适的ARIMA模型进行拟合。如果误差值通过白噪声检测，就可以采用拟合出的模型对时序数据进行预测了。

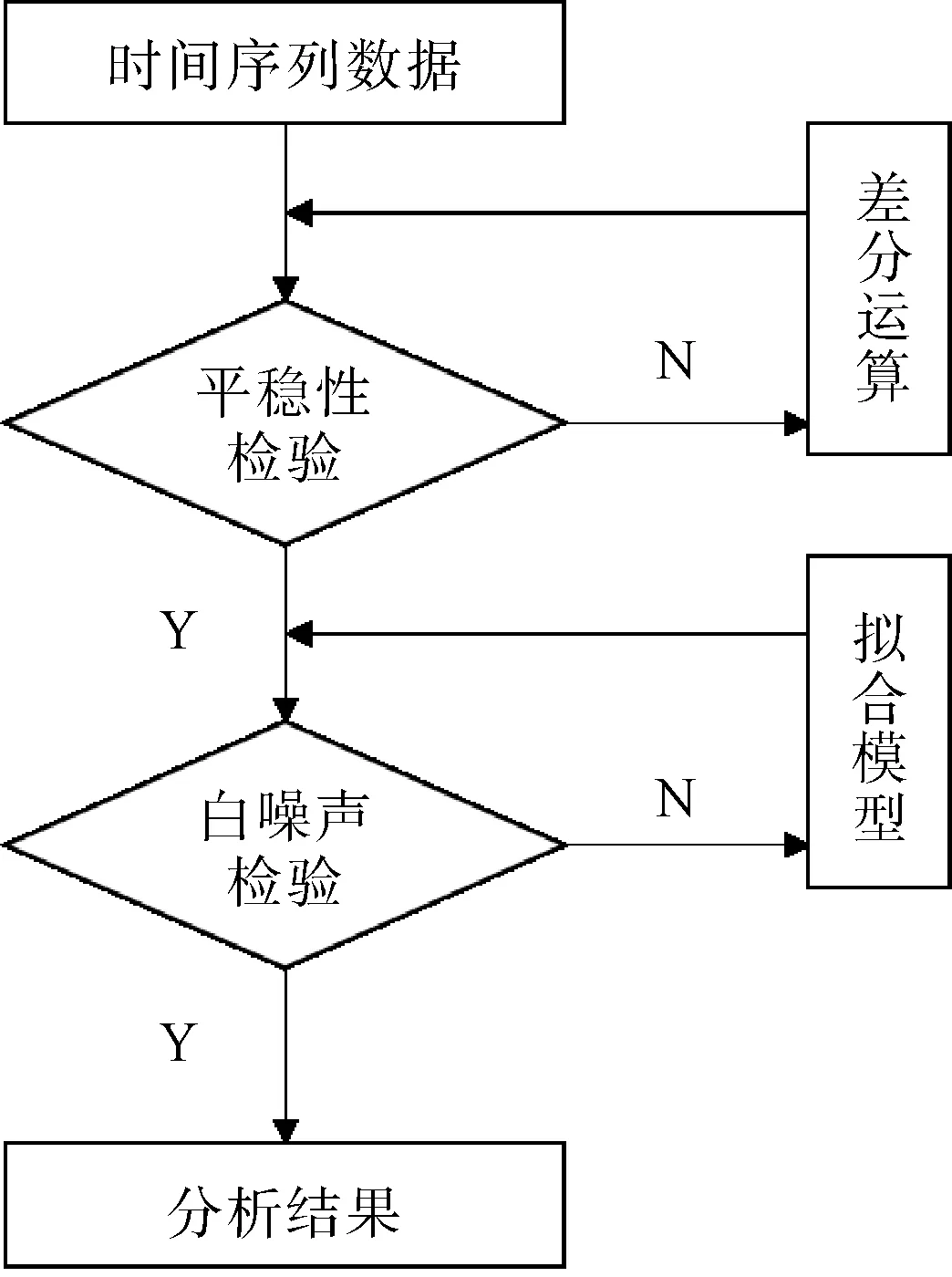
图3 ARIMA建模步骤

3.2 LSTM

DNN(Deep Neural Networks，深度神经网络)在人工智能领域应用极其广泛，主要在图像分类以及目标检测方面取得了很大的进展，但是由于DNN仅仅考虑上一层神经网络对当前网络层的影响，没有时序的概念，不能对时间序列数据进行分析，因此出现了在DNN基础上的RNN(Recurrent Neural Network，递归神经网络)。RNN使上一刻的输出能够对现在状态的输入产生影响，特别适合学习具有时间依赖性的时序数据。由于RNN增加了跨越时间点的自连接隐含层，因此可以对时间变化数据进行建模。但RNN只能够接受上一个节点的输出，随着网络层次的加深，可能会发生梯度消失或者梯度爆炸，就是当前节点无法对距离自己较远节点的信息进行“记忆”[11]。为了解决该问题，研究人员提出了很多解决办法，其中最为经典的一个网络模型是LSTM(Long Short-Term Memory，长短时间记忆模型)。

LSTM是经过改进的RNN，其设计的优点是可以在很大程度上避免梯度消失。LSTM网络可以通过记忆单元来学习时间序列长短期依赖信息，因此，其在处理和预测具有较长间隔和延迟事件的时间序列方面，应用效果显著[12]。LSTM模型相对于其他深度神经网络的不同是在模型中加入了“记忆单元”(Memory Cell)来判断当前信息是否有用。在这个记忆单元中存在三种门，分别是输入门、遗忘门和输出门，当信息进入到LSTM后，模型根据规则来判断其是否有用，只有符合要求的信息才会被留下，不符合的信息会被直接“遗忘”，这样可以解决时间序列数据在训练过程中的“记忆”问题。

LSTM的建模过程一般分为模型输入、模型训练和模型预测三部分。模型整体框架如图4所示。其包括输入层、隐含层、输出层、模型训练以及模型预测5个功能模块。输入层是一个全连接层，通过对样本数据进行初步处理，以满足LSTM的输入要求；隐含层是由多个LSTM神经元构成的递归神经网络；输出层是将隐含层的多个实际结果重新通过一个全连接网络映射成模型期望的结果；模型训练是对损失函数进行最小值优化的训练过程；模型预测是将得到的预测结果可视化。

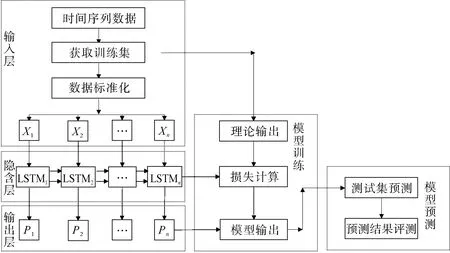
图4 LSTM建模过程

3.3 评价指标

为了全面地评价模型的预测效果，反映预测值与实际值之间的误差大小，本文采用了均方根误差(RMSE)作为模型评价指标。其定义为式(3)：

(3)

式中：ERMS为均方根误差；f(i)为预测值；h(i)为实际值。

4 数据分析结果以及比较

4.1 数据结果分析

本文的目的是为了分析在轨道交通延时运营中，ARIMA和LSTM两种方法对5 min间隔和15 min间隔数据的预测中，哪种方法更有效、误差更小。使用Python语言中statsmodels库中的ARIMA模型进行了ARIMA算法的实现，keras库中的LSTM模型进行了LSTM算法的实现。

首先使用传统的15 min间隔对两种方法进行了比较，结果如图5、图6所示。不管是ARIMA方法还是LSTM方法，在15 min间格的数据进行预测时，主要的误差出现在上午时段(见图中圆内差异)，且LSTM方法(图6)显示出较高的准确性。

然后再对5 min间隔的数据进行预测，结果如图7、图8所示。同15 min间隔数据，不管是ARIMA方法还是LSTM方法，在5 min间格的数据进行预测时，主要的误差也出现在上午时段(见图中圆内差异)，同样LSTM方法(图8)显示出较高的准确性。

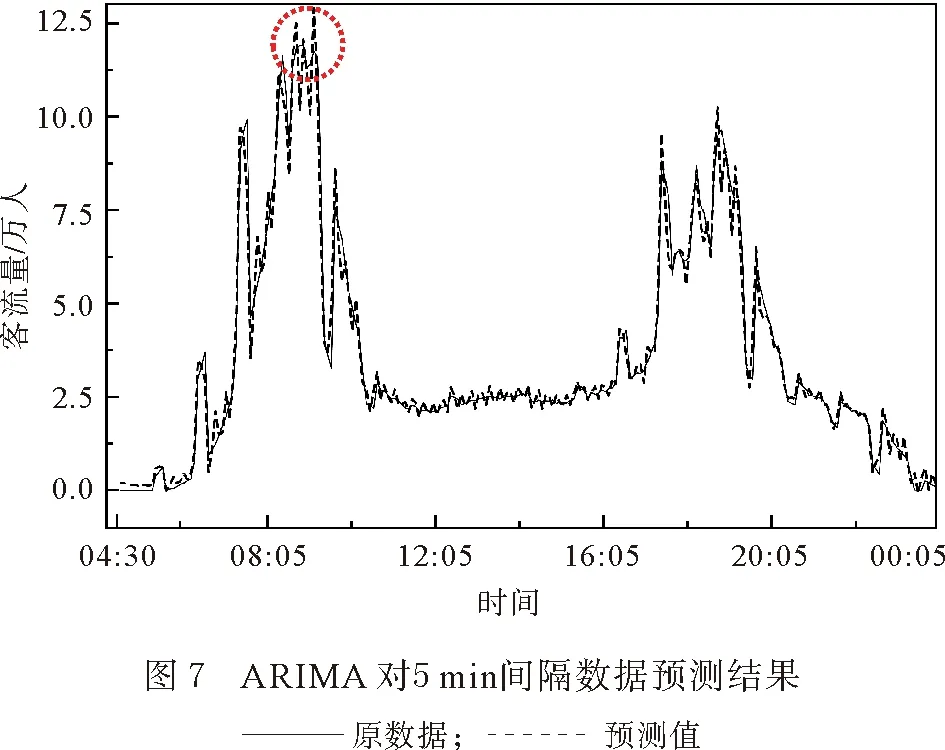
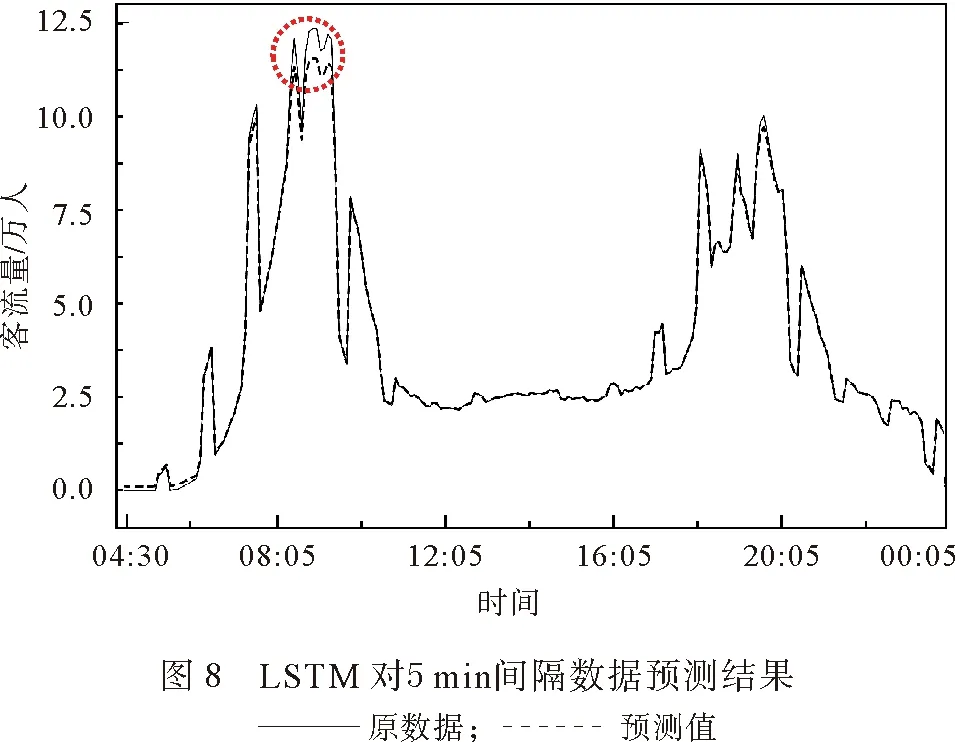
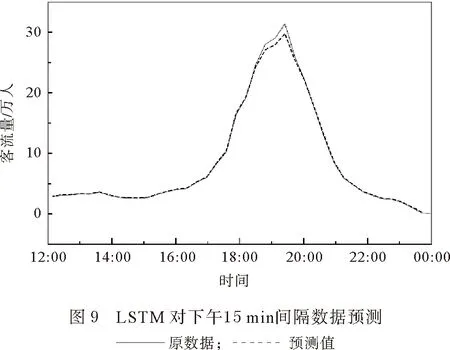
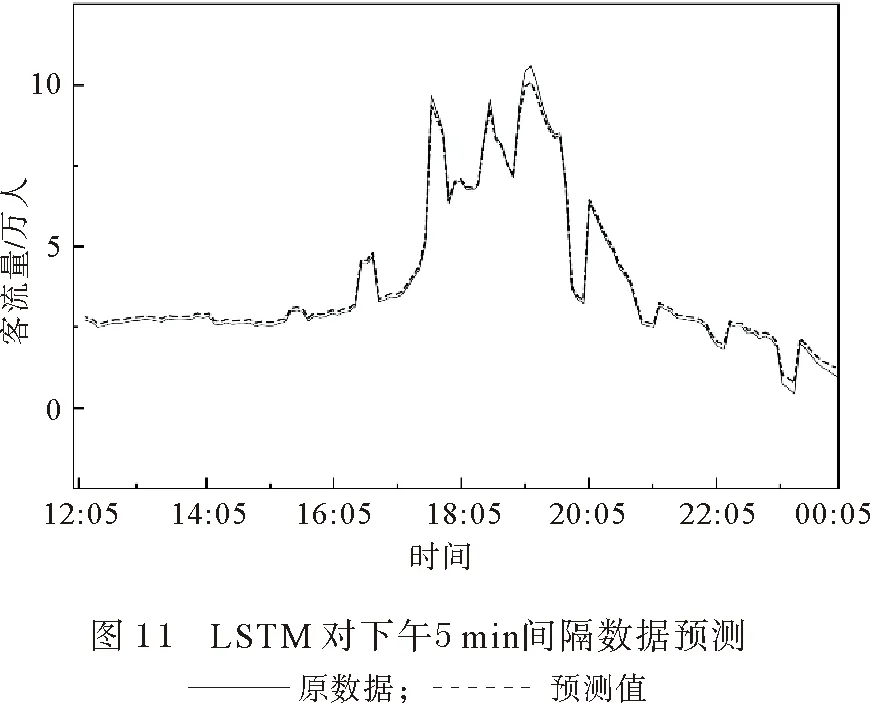
由图5—8 可以看出，在对5 min间隔的数据进行拟合时，不管ARIMA方法还是LSTM 方法，都比15 min间隔数据的准确性要高。但是两种方法同时显示出，上午早高峰的拟合要比下午晚高峰的拟合误差要高。本文主要是对晚上延时运营进行预测，因此为了排除早高峰的数据对误差的影响，将中午12：00前的数据剔除后，仅留下下午数据用ARIMA和LSTM方法重新拟合。结果显示对下午数据的预测中，使用LSTM方法对15 min间隔数据进行预测(图9)准确性要比ARIMA方法对15 min间隔数据进行预测(图10)的准确性要高；使用LSTM方法对5 min间隔数据进行预测(图11)准确性要比ARIMA方法对5 min间隔数据进行预测(图12)的准确性要高。

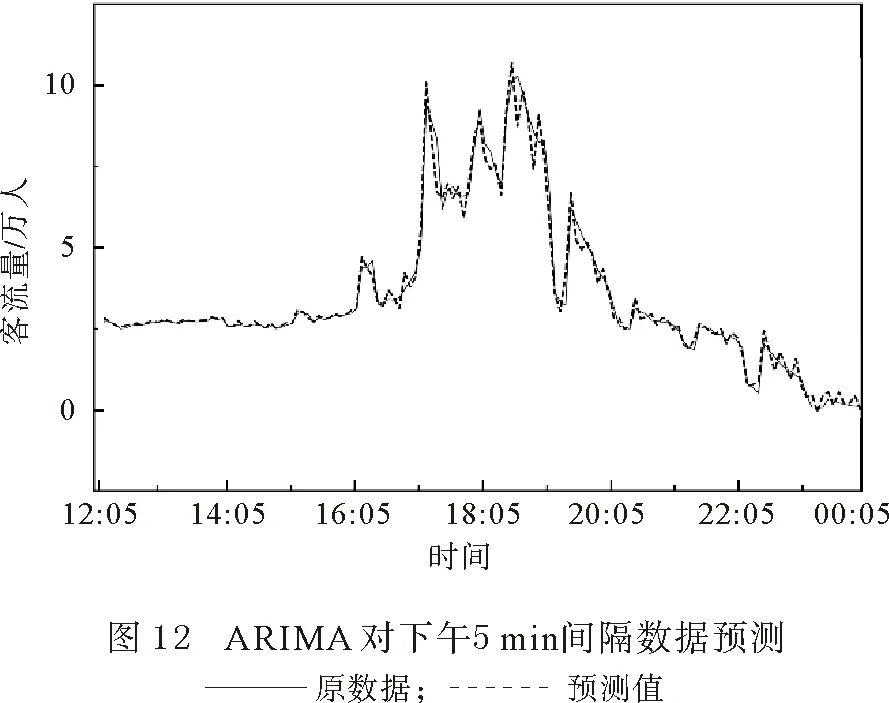
4.2 预测结果分析

不同预测数据以及方法的精度结果如表1所示。根据数据量、预测方法和时间间隔的不同，均方根误差的结果也不同，RMSE越小说明模型的精度越高。整体来看，半天数据相对全天数据普遍均方根误差较小，显示出模型的拟合度较高，具有较好的预测效果。从方法上比较，LSTM方法比ARIMA方法的均方根误差小，具有较好的预测效果。从时间间隔上比较，5 min间隔相对15 min间隔的预测效果要好。

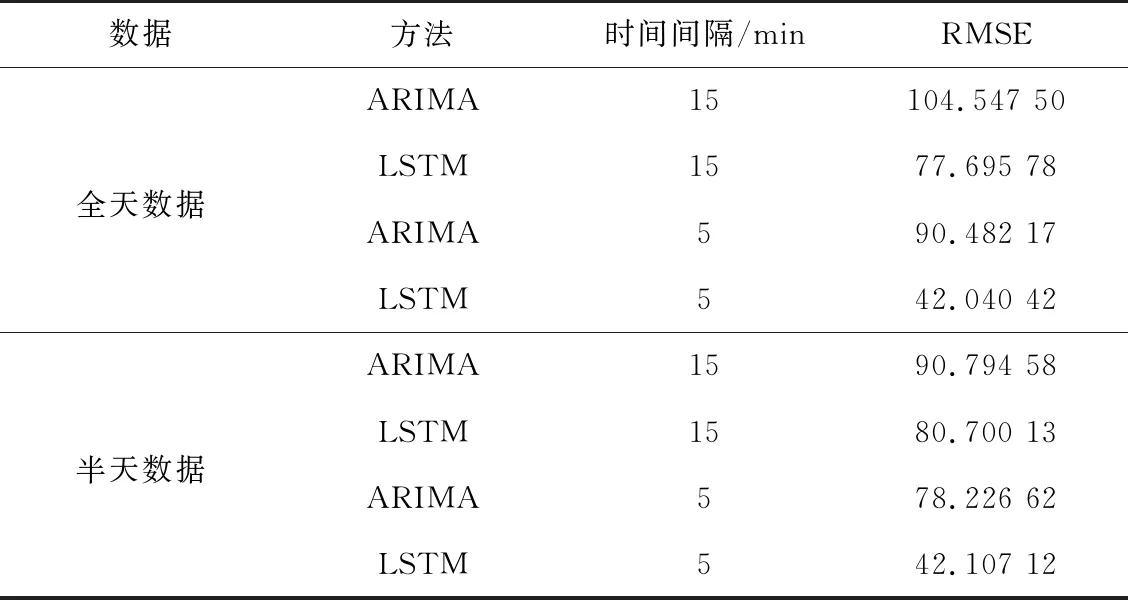
表1 不同时间粒度与不同数据量的RMSE结果

从具体数值上来看，全天数据和半天数据的LSTM方法的预测效果基本相同，全天数据15 min间隔的LSTM方法和半天数据5 min间隔的ARIMA方法以及半天数据的15 min间隔LSTM方法的预测效果基本相同。

5 结论

本文对不同时间粒度、不同时间段的地铁客流数据，采用ARIMA模型和LSTM模型进行了客流预测。研究发现：相比短时客流数据分析常用的全天数据，采用半天数据(12:00后时段)进行预测，ARIMA模型和LSTM模型的预测精度都有显著提升，说明4：30—12：00数据对预测产生了负影响。时间粒度选择上，采用5 min间隔数据，ARIMA和LSTM两种预测模型的精度都会有一定的提升，但LSTM预测效果更为突出。

在目前研究的基础上，后续研究可进一步将深度学习的其他预测模型与之对比，并针对工作日以及周末、地铁站分类、上车和下车乘客的延时客流量预测细化研究。