基于性能退化的单盘转子碰摩可靠性分析

苏长青，赵美琪

(1.沈阳航空航天大学 安全工程学院，沈阳 110136；2.辽宁省飞机火爆防控及可靠性适航技术重点实验室，沈阳 110136)

1 引言

转子系统的全寿命周期历经正常到退化直至失效的全过程，在这期间系统的主要性能参数会随着时间经历不同的退化状态，当退化累积到一定程度时系统将失效。在转子系统众多故障中，转静碰摩具有不可避免且危害性大的特点，因此研究转子碰摩性能退化对可靠性分析具有十分重大的意义。

过去近百年的时间里，学者就转子碰摩机理做出了许多深入的研究。随着研究的深入，学者发现转子系统并非简单的线性运动，实则存在大量的非线性运动。A.Muszynska[1]指出旋转机械发生转静子碰摩现象的同时，转子系统内存在大量非线性行为，严重时甚至发生混沌现象。ChangJie等[2]研究了Jeffcott转子的非线性振动特性，引入了Lyapunov指数，他们发现碰摩发生的剧烈程度与指数呈现明显的正相关性。Chu等[3]伴随着转子系统发生碰摩，瞬态频率也在剧烈变化，通过研究动力学模型发现，刚度的瞬时变化可作为碰摩发生剧烈程度的标识。Mohamed[4]通过大量的研究发现，转子碰摩对共振频率有着显著地影响，随着碰摩发生剧烈，共振频率变强。张义民[5]针对由质量偏心引起的转子系统碰摩,应用四阶矩技术,摄动理论等，对转子系统可靠性灵敏度、可靠性等给出了系统的计算方法，并用数值解析进行验证。李东[6]针对弹性支承裂纹—碰摩转子系统物理模型,应用有限元软件和裂纹扩展理论分析裂纹扩展情况，并计算转子系统的剩余寿命。

本文以单盘Jeffcott转子模型为例，考虑到实际服役过程中系统质量、刚度会随着时间逐渐退化，建立了考虑性能退化的动力学微分方程，主要是质量慢变、刚度退化情况。应用Kronecker代数、随机摄动技术、二阶矩技术求解其可靠度和可靠性灵敏度。在对转子系统可靠性进行分析时，未限制随机变量的分布，因此得到的可靠性分析结果更具有实际意义。

2 模型建立

2.1 刚度退化模型

根据动力学方程，影响转子性能的参数是刚度、质量、阻尼，因此刚度是转子碰摩一个重要的性能参数。本文选用的刚度累计损伤理论是以Miner-Palmgren 提出的Miner理论作为转子碰摩刚度退化的模型基础。其表达式为：

(1)

式(1)中：D表示损伤指数，A、B表示材料相关常数，γt表示循环应变幅，Q·t表示连续无间断震动中的循环次数。根据转子系统的材料结构，当式中A=9.06×10-5，B=2.06,γt=0.001 5 m时可得到转子碰摩刚度退化随时间变化曲线，如图1。

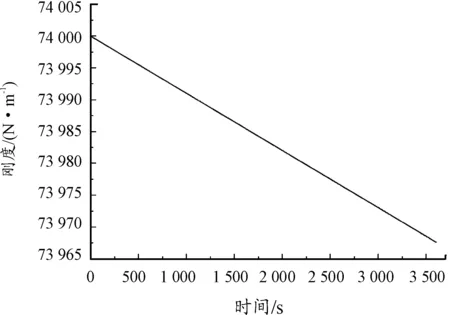
图1 刚度随时间变化曲线

2.2 质量慢变模型

转子系统实际运行过程中，转子质量非恒定不变，而是随着系统运行因损耗、磨损、粘接等原因发生质量慢变。假设某离心机转轴刚度为k,转子质量为m(τ),静子刚度为kr，ω为转子角频率,m0为转子质量的均值,离心机在工作中转子质量围绕均值变化，则

m(τ)=m0(1+λcos(ωτ))

(2)

式中：λ为质量变化幅值系数，τ=εt为慢变时间，ε为慢变时间系数。

当上式中λ=0.2，ε=0.1，m0=0.6时，质量慢变随时间变化曲线如图2。

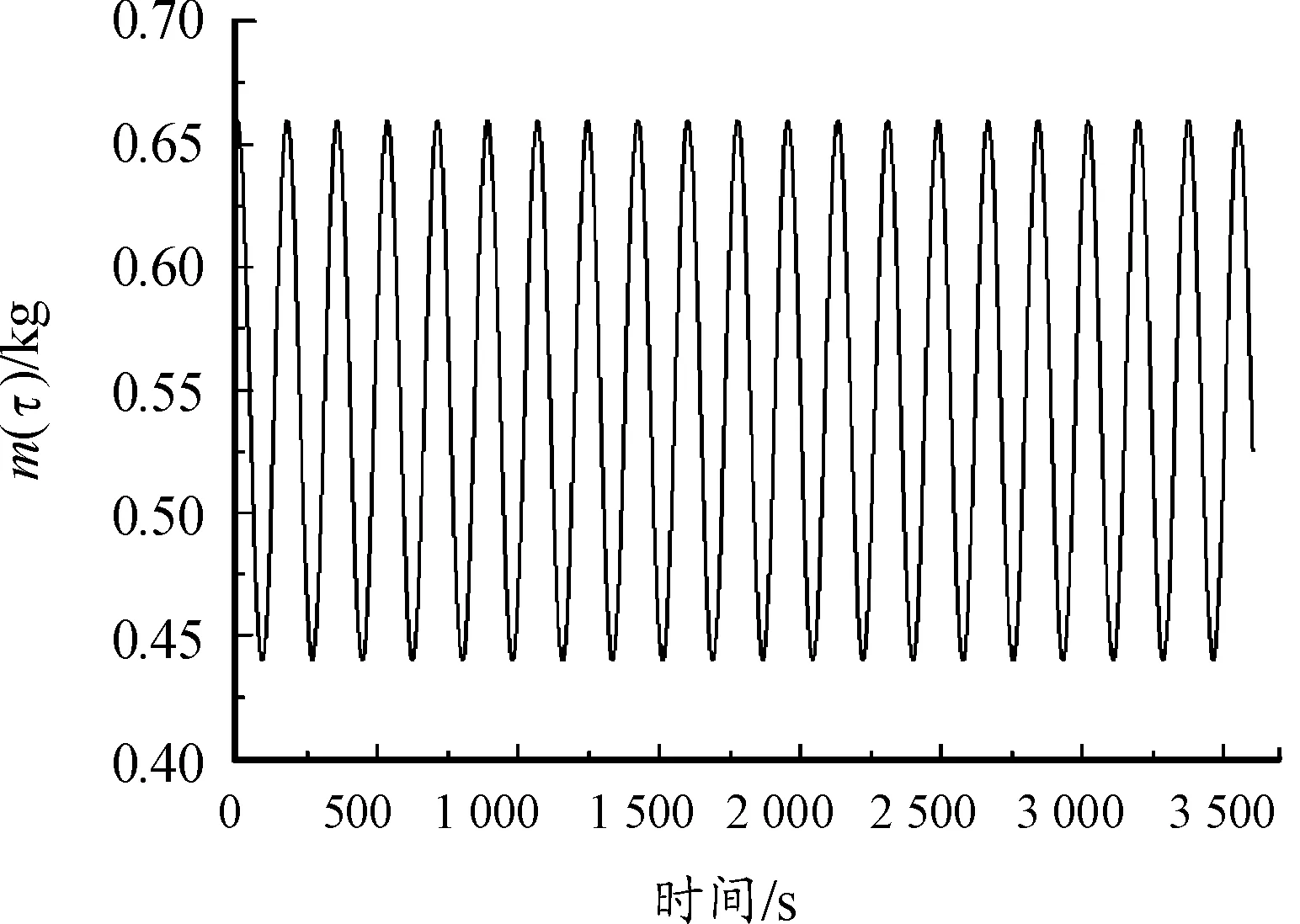
图2 质量慢变随时间变化曲线

2.3 考虑性能退化转子动力学模型

本文建立以油膜力为支撑力单盘Jeffcott系统，其结构如图3所示。

图3 转子碰摩系统结构示意图

假设转轴等效集中质量m1、刚度k1、阻尼c1，转盘质量m2、阻尼c2、偏心距为e，转盘振幅r，静子刚度为kr，转速为ω，转、静件同心、间隙为δ，结构各向同性，Fx、Fy是油膜力，Px、Py是碰摩力。考虑转子性能退化情况(质量慢变和刚度退化)，根据牛顿定律建立转子碰摩非线动力学微分方程。

(3)

式中：m2(τ)是质量慢变函数，S(t)是刚度退化函数。

3 随机响应

已知转子的动力学方程为

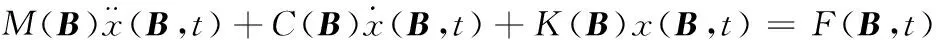
(4)

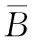
(5)

(6)

(7)

(8)

(9)

式中⊗为Kronecker乘积。

(10)

4 可靠性分析和可靠性灵敏度

根据应力—强度干涉理论状态函数可定义为：

Z=δ-ri

(11)

可算出系统的瞬态可靠度R：

(12)

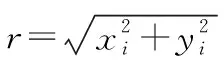
μZ=E(Z) =g(μx1,μx2…μxn) =μδ-μri

(13)

(14)

瞬态可靠度系数为：

(15)

此时瞬态可靠度为：

R(βi)=1-φ(-βi)

(16)

本文使用一次二阶矩计算可靠性灵敏度，可靠性灵敏度为可靠度R(βi)对随机变量分布函数的偏导数。

(17)

(18)

(19)

将状态函数代入式(19)可得

(20)

则可靠性灵敏度为

(21)

5 数值算例

某一离心机转子系统，静子质量m1为0.4 kg，转盘质量m2为0.55 kg，轴承阻尼、转盘阻尼分别为500 N·s/m、550 N·s/m，圆盘偏心距e为0.1 mm，转轴刚度k1、静子刚度kr分别为74 000 N/m、146 000 N/m，转静摩擦因数0.1，随机变量B=[k1,m2,c2,e,kr],分别为正态函数，间隙δ的前二阶矩为3 mm，0.421 mm2。

经过计算得到不同可靠度下转轴刚度k1、转盘质量m2、转盘阻尼c2、偏心距e、静子刚度kr的均值可靠性灵敏度如图4～图7所示，并绘制转轴刚度k1、转盘质量m2、转盘阻尼c2、偏心距e、静子刚度kr的均值可靠性灵敏度随时间变化如图8～图12。

图4 可靠度R=95%时随机参数均值可靠性灵敏度直方图

图5 可靠度R=85%时随机参数均值可靠性灵敏度直方图

图6 可靠度R=75%时随机参数均值可靠性灵敏度直方图

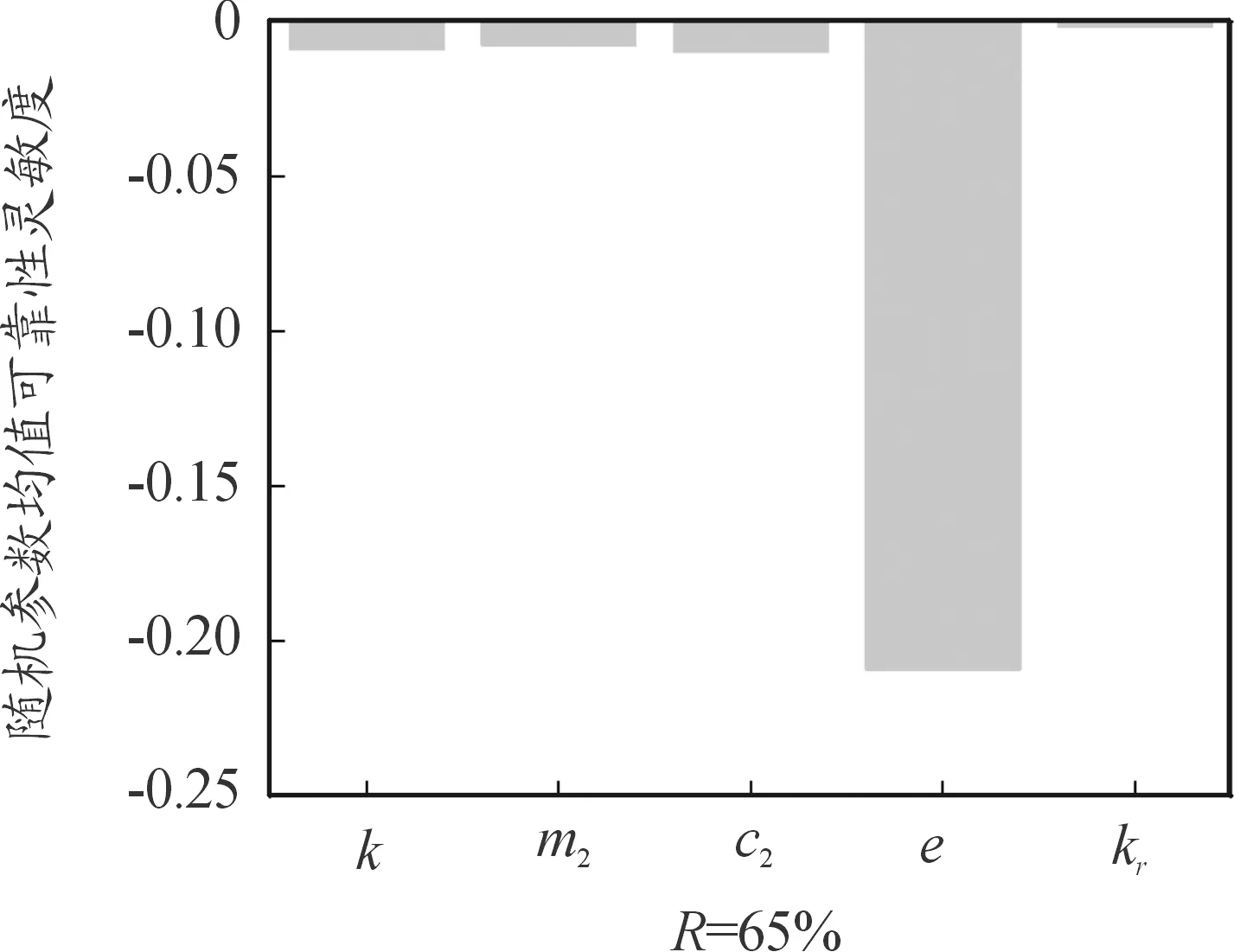
图7 可靠度R=65%时随机参数均值可靠性灵敏度直方图

图8 可靠性灵敏度DR/Dμk曲线

图9 可靠性灵敏度DR/Dμm2曲线

图10 可靠性灵敏度DR/Dμc2曲线

图11 可靠性灵敏度DR/Dμe曲线

图12 可靠性灵敏度DR/Dμkr曲线

通过图4～图7可以观察到在可靠度分别为95%、85%、75%、65%的条件下，转轴刚度k1、转盘阻尼c2、静子刚度kr均值可靠性灵敏度基本为正值，说明转轴刚度k1、转盘阻尼c2、静子刚度kr对转子系统产生积极的影响，即增大转轴刚度k1、转盘阻尼c2、静子刚度kr均值，会使转子系统趋于可靠；转盘质量m2、偏心距e均值可靠性灵敏度为负值，说明随着转盘质量m2、偏心距e均值增加，转子系统趋于不可靠，即发生碰摩的概率增加。

观察图8～图12，可靠性灵敏度在系统刚刚启动时由于振荡出现较大波动，经过一段时间后趋于稳定，从图13可以看出2 400 s之后在刚度退化和质量慢变的作用下，转子系统可靠度下降，系统发生碰摩的概率增加，因此可靠性灵敏度再次发生波动。根据幅值变化定性分析得出偏心距e的均值可靠性灵敏度最大，达到了10-1数量级，因此偏心距对系统可靠度响应灵敏，在可靠性分析和设计时应严格控制偏心距变化；转轴刚度k1、阻尼c2、转盘质量m2次之，为10-3数量级，在设计中应充分考虑转轴刚度k1、阻尼c2、转盘质量m2的变化对可靠性的影响；静子刚度kr的均值可靠性灵敏度最小，数量级只有10-11，说明系统可靠性受静子刚度kr因素影响不明显，可将其视为确定量，降低计算难度。

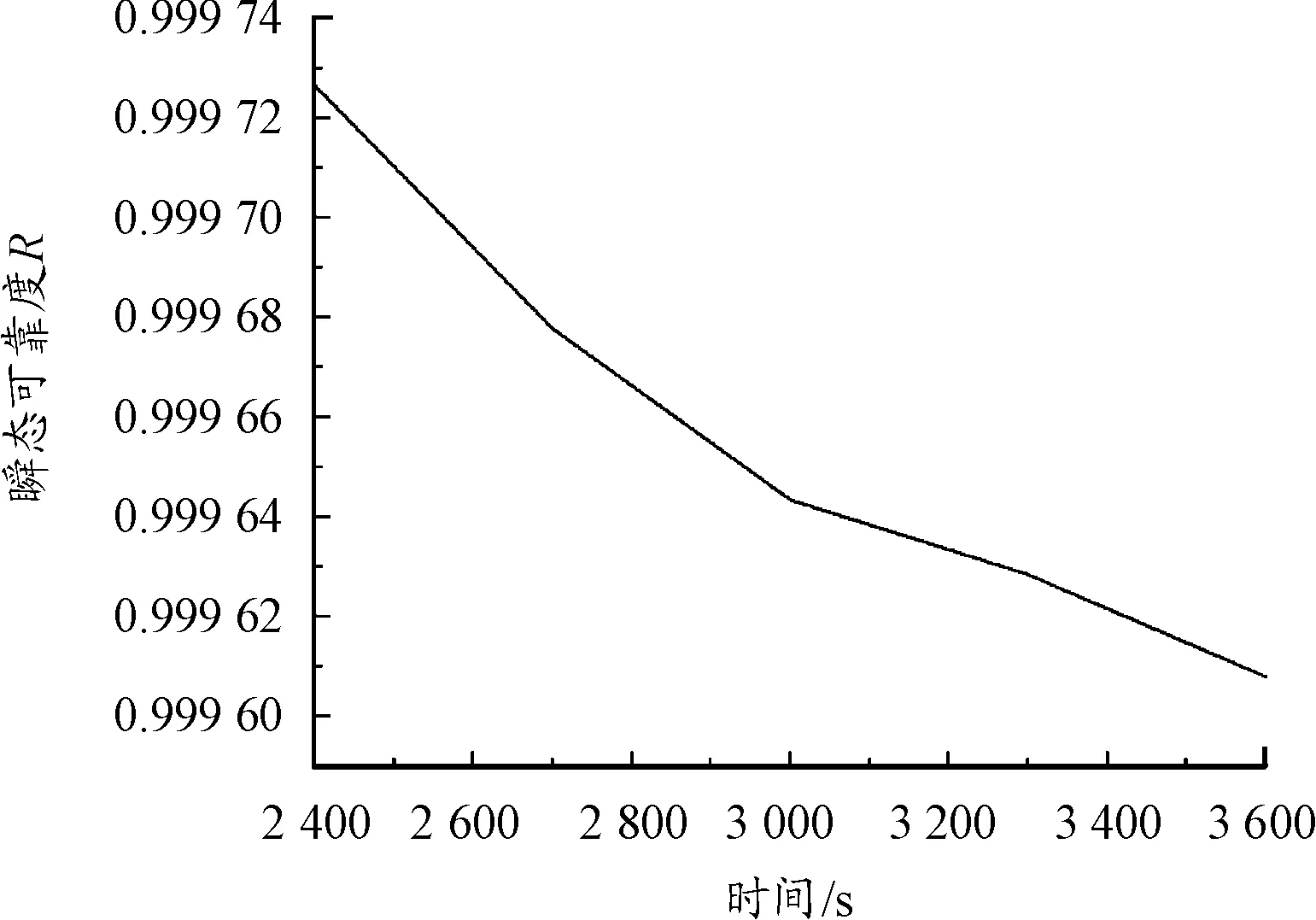
图13 瞬态可靠度R曲线

6 结论

提出了转子系统可靠度和可靠性灵敏度的分析方法，研究了刚度退化和质量慢变对于系统可靠性的影响规律。转轴刚度k1、转盘阻尼c2、静子径向刚度kr均值增加将使系统可靠度增加，偏心距e、转盘质量m2均值增加将使系统可靠度降低；偏心距e对转子系统响应灵敏明显高于其他4个随机参数，在机械设计和分析中必须考虑其变化。