固体火箭喷焰的尘埃等离子体非相干散射研究

冯杰 郭立新 徐彬 吴健 许正文 赵海生 马征征

（1. 中国电波传播研究所 电波环境特性及模化技术重点实验室，青岛 266107；2. 西安电子科技大学物理与光电工程学院，西安 710071）

引 言

火箭尾气(如H2O)以超音速喷射进入电离层，与背景电离层离子交换电荷时，产生的高速拾取离子(H2O+)束可以在高层大气中产生广泛的效应. 这些效应包括：增强的光辐射，大范围的大尺度等离子体湍流，通过复合降低等离子体密度，产生电离层洞及改变无线电波传播环境等. 用雷达和光学仪器探测火箭尾焰产生的电离层等离子体效应可反演火箭羽流的物理特性.

早在1959年Vanguard Ⅱ发射后，人们已开始使用地基/天基雷达对火箭喷焰电离层效应进行观测与研究[1]. 1973年5月14日，美国航空航天局(National Aeronautics and Space Administration, NASA)在土星V火箭(Saturn V)发射天空实验室时，使用卫星信标和垂测仪进行了观测，结果发现火箭尾焰形成的等离子体总电子含量(total electron content, TEC)减少了近50%，并持续了4 h[2-3]. 1979年9月20日，美国利用大力神洲际导弹/半人马火箭发射了NASA的第三颗高能天体物理观测卫星，非相干散射雷达(incoherent scattering radar, ISR)获取了大尺度电离层洞空间分布特征，电离层洞持续了3 h，电子密度耗空达80%[4-6].

近些年，关于火箭尾焰的研究，朝鲜、日本的报道相对频繁. 大浦洞1号和2号导弹[7]、种子2号火箭[8]、银河3号和光明4号[9]发射时，利用日本稠密GPS站网对火箭引起的电离层效应进行了观测，发现发射均引起了不同程度的电子密度耗空. 美国就可回收式猎鹰9号火箭的发射研究了电子吸附和产生的冲击波两种机制引起的TEC耗空效应[10-11].

探测火箭尾焰电离层效应时，电离层ISR发现了诸多特性，其中环形离子分布(也称Bump-on-tail分布)是非常重要的特性之一. 对这一特性进行研究有助于了解电离层，同时也可对尾焰识别进行探测.Bernhardt等人在SIMPLEX III和SIMPLEX IV期间进行了航天飞机喷焰的ISR针对性实验，利用航天飞机发动机产生大范围的相对背景中性等离子体的大束专用等离子体对流，排气分子与电离层中O+离子交换电荷得到Bump-on-tail分布[12-14]. 并通过在SIMPLEX Ⅱ实验中获得的火箭喷焰ISR谱进行曲线拟合，确定了环形离子束分布的形成[15]. 天空2号实验室发射时，Millstone Hill的ISR也接收到了类似的雷达信号[16-17]. 为了远程测量固体火箭电离层效应，2009年9月，美国海军研究实验室进行了带电气溶胶释放试验(the charged aerosol release experiment,CARE)，测量了尘埃粒子分布和电离层火箭尾气的相互作用[18-19].

Bump-on-tail分布引起的后向散射增强是由等离子体中的扰动现象产生的，这些现象“看起来”是电子密度的累积，但Schunk和Szuszczewicz[20]及Bernhardt等人[21]提出的静电扫雪机并不适用于这个问题，这个过程只压缩膨胀的离子密度和增强边缘的离子密度. 本文在徐彬等人[22-23]工作的基础上，讨论火箭羽流中离子的非平衡分布对非相干散射谱的影响. 火箭喷焰中拾取离子的非平衡速度分布类似于强对流极光区电离层、彗星中性原子电离、太阳环与行星际磁场碰撞中的分布，因此其非相干散射研究同时可用于自然扰动等离子体的研究.

文章中基于尘埃等离子体非相干散射理论对固体火箭喷焰早期等离子体Bump-on-tail分布的非相干散射特性进行了模拟，对比分析了尘埃掺杂和分布函数对非相干散射谱的影响，并对其影响机制进行了初步解释.

1 基于Bump-on-tail分布的尘埃等离子体散射理论

铝粉是固体火箭推进剂中一种重要的金属燃烧剂，与其他金属燃烧剂相比，铝粉对提高推进剂的比冲有显著的作用，并且对抑制不稳定燃烧也有显著的作用. 随着铝粉含量的增加，固体火箭推进剂的能量特性提高，比冲增加，可以满足火箭发动机在动力方面的要求. 由于其燃烧可生成零点几微米到几百微米尺度的固体尘埃产物(主要为Al2O3)，因此固体火箭喷焰是高温高密度离子、电子、尘埃三者的混合非均匀尘埃等离子体羽流.

平静电离层状态下，电离层中没有不稳定性源，呈各项同性，粒子速度分布为Maxwellian分布：

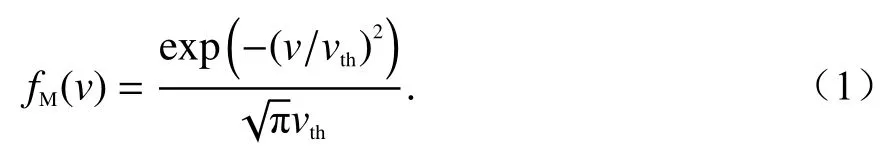
火箭穿过电离层时，背景离子的热速度远低于火箭尾气注入速度，当超音速的中性粒子(H2O)与背景离子(O+)交换电荷时，将生成拾取离子H2O+.最初，拾取离子将在固定离子频率和离子回旋半径的轨道上运动. 离子回旋频率远小于电子回旋频率，离子回旋半径远大于电子回旋半径，因此通常认为电子相对于离子是被磁化的. 电子热速度远大于中性粒子或离子速度，电子速度分布不会被尾气直接改变，服从Maxwellian分布. 拾取离子被电离层背景中性粒子碰撞阻尼前，形成了离子环形速度分布，即服从Bump-on-tail分布. 带电尘埃粒子质量远大于电子和离子，可被看成是重离子，亦服从Bump-ontail分布.

Bump-on-tail分布函数可写为如下分段的Maxwellian函数形式：

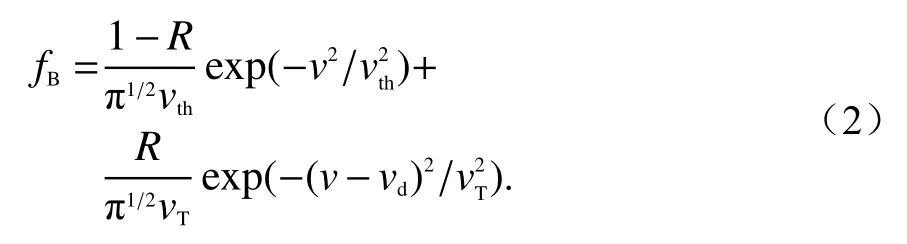
式中：R为尾向分布粒子比率；vth为背景离子热速度；vd为尾向分布粒子漂移速度；vT为漂移高能粒子热速度，，κ为 非Maxwellian指 数，κ=∞时，分布函数退化为Maxwellian分布.

为了便于分析，在下节中，我们称前半段为离子/尘埃的Maxwellian分布部分，后半段为离子/尘埃的Bump-on-tail分布部分.

图1为离子速度分布随高能粒子(拾取离子)组分的变化情况. 可以看到：当R=0时，式(2)退化为Maxwellian分布，速度分布满足高斯分布；当R=0.2时，在原速度分布右侧出现了新的峰值，形成Bumpon-tail分布，相当于将一个幅度较小的Maxwellian分布进行了右移，幅度在式(2)中体现为热速度(离子温度)的变化，右移则用漂移速度来体现；当R=0.4和R=0.6时，从速度分布的二维变化图可以看出，随着R的增大，速度分布偏离原速度中心的量逐渐增大，并在某一速度区域聚集，形成环状离子速度分布.

图1 离子速度分布随高能粒子组分的变化Fig. 1 The ion velocity distribution varies with the composition of high-energy particles

对存在速度分布的尘埃等离子体来说，忽略磁场和碰撞，其功率谱为[23]

式中：k=4πfrad/c为雷达波数，frad为雷达频率；ε=1+Ge+Gi+Gd为介电函数；ω=2πf为多普勒角频率；Zi和Zd分别为离子电荷数和尘埃电荷数；fe0、fi0和fd0分别为电子、离子和尘埃的速度分布函数；ne、ni和nd分别为电子、离子和尘埃的密度；χe、χi、χd分别为电子、离子和尘埃的极化率，

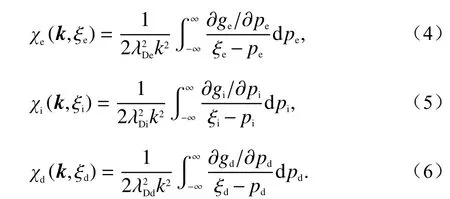
式中：λDe、λDi和λDd分别为电子、离子和尘埃的德拜长度；ge、gi和gd分别为电子、离子和尘埃的归一化分布函数；pe=v/vthe、pi=v/vthi、pd=v/vthd分别为电子、离子和尘埃的归一化速度，vthe、vthi和vthd分别为电子、离子和尘埃的热速度；ξe=ω/(kvthe)、ξi=ω/(kvthi)和ξd=ω/(kvthd)分别为电子、离子和尘埃的归一化角频率.

对任意速度分布函数，根据留数定理和小圆弧定理，式(4)、(5)、(6)可以进一步写为

式中，α≡1/(kλDe).

将式(1)、(2)、(7)、(8)和(9)代入式(3)即可得基于Bump-on-tail分布的非相干散射谱，进而得到较为完备的基于Bump-on-tail分布的尘埃等离子体非相干散射计算方法：

2 固体火箭早期尘埃等离子体非相干散射谱数值模拟

本节对固体火箭喷焰与背景等离子体高速对流场景形成的尘埃等离子体的非相干散射谱进行模拟计算. 场景参数为：背景电离层电子温度为2 690 K，离子温度为1 480 K，高能粒子(拾取离子)及中性粒子温度均为300 K(两种粒子温度主要由冷凝过程中释放的热量控制，如果没有这个过程，由于中性粒子迅速膨胀其温度将冷却至100 K以下[12])，尘埃密度为1013m−3，尘埃半径为0.1 µm[24]. 尘埃等离子体非相干散射谱包含电子、离子和尘埃三部分的贡献，对应的非相干散射谱包含电子谐振区、离子谐振区(为区别于传统计算，本文我们称包含尘埃组分的等离子体的离子谐振区为尘埃离子谐振区)和尘埃谐振区.非均匀分布Bump-on-tail函数的引入改变了离子分布参数，尘埃粒子由于质量很大，对高频电子谐振区的贡献很小，因此本文主要对离子谐振区进行模拟分析.

图2为离子谐振频率附近vd=3 km/s 时不含尘埃组分的离子谱线随高能粒子组分的变化情况. 可以看出，Maxwellian分布和离子Bump-on-tail分布产生的谱线有显著区别：Maxwellian离子谱线表现为典型的离子双峰结构，而引入了Bump-on-tail分布以后，出现了多峰分布.

图3给出了当R=0.4时，多峰离子谱线的成因，其中，红色虚线部分为60%的Maxwellian分布离子组分产生的谱线，绿色虚线表示40%的Bumpon-tail分布离子产生的谱线，R=0.4时的蓝色谱线为上述两条谱线的合成. 在离子谐振区，离子为主控因素，一部分离子的Bump-on-tail分布使得谱线最大峰值稍有下降，但离子的漂移产生了新的峰值，导致离子谱线出现了三峰结构. 且从图2中可以看出，随着高能粒子组分的增加，中间最大驼峰右移，右侧新增驼峰的峰值逐渐大于左侧驼峰，此时Bump-on-tail分布在离子谐振频率处的占比已经超过了Maxwellian分布，故其对离子谱线的贡献也相应增大.

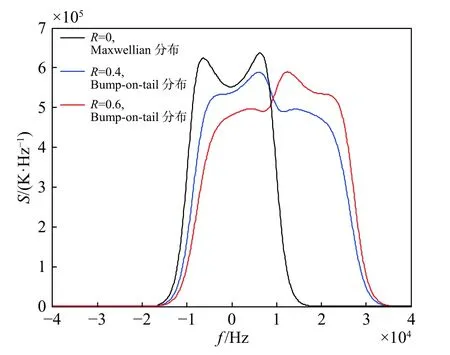
图2 vd = 3 km/s 时离子谱线随高能粒子组分的变化Fig. 2 The ion spectrum varies with the composition of highenergy particles, when vd = 3 km/s

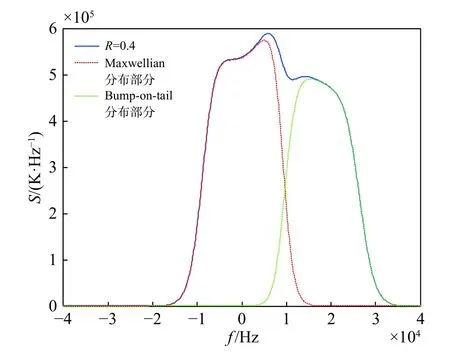
图3 R=0.4，vd = 3 km/s 时离子谱线的分段合成Fig. 3 The synthetic spectrum composed by segmented ion distribution, when R=0.4, vd = 3 km/s

图4为R=0.4时离子谱线随高能粒子速度的变化情况. 可以看出：随着高能粒子速度的增大，谱峰先是上升，而后又降低；谱线由最初的典型双峰结构先变为单峰，而后变为多峰结构；谱宽基本随着速度的增加而增加.

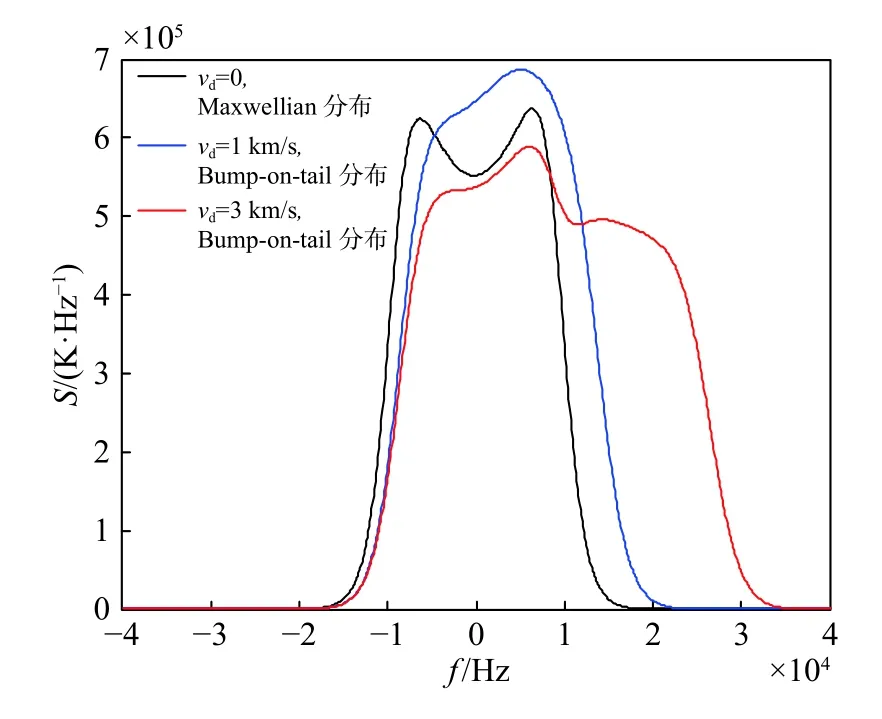
图4 R=0.4时离子谱线随高能粒子速度的变化Fig. 4 The ion spectrum varies with the velocity of highenergy particles, when R=0.4

图5给出了当R=0.4漂移速度vd不同时Bumpon-tail分布部分的离子谱线. 可以看出，当vd=2 km/s时，Bump-on-tail分布的离子部分对谱线幅度的贡献达到最大，说明该速度处于此参数条件下的离子谐振频率附近.

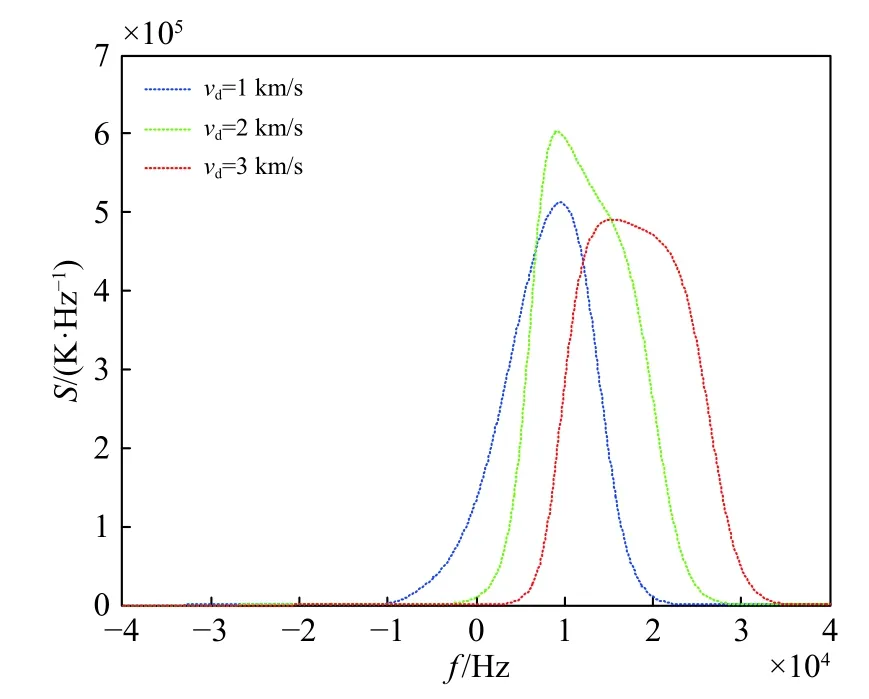
图5 R=0.4时Bump-on-tail分布部分的离子谱线随高能粒子速度的变化Fig. 5 The ion spectrum of the bump-on-tail distribution varies with the velocity of high-energy particles, when R=0.4

图6为vd=3 km/s时掺杂有尘埃的尘埃离子谱线随高能粒子组分的变化情况. 通过对比图2中R=0时Maxwellian分布的离子谱线可以看出，尘埃组分的加入使得离子谱线的幅度增加了两个量级，双峰间距增大，谱宽展宽，由于带电尘埃可视为“重离子”，故它的引入既可以吸附离子，又可以通过调整德拜半径影响离子谱线[23]. 对比图6中三条谱线可知：在尘埃离子谐振区，非相干散射谱为双峰结构，两个峰值相差不大，左峰值略大于右峰值；随高能粒子组分的增加，谐振谱线间距离逐渐变小，上下行离子线谱的谱宽变窄，非相干散射谱逐渐从有一定分布的谱线结构转变为单一的谐振线. 图6中，R的增加使得Maxwellian分布离子减少，一方面改变着谐振频率，使谱幅度增强；一方面使得离子和尘埃的Maxwellian分布减少，即处于谐振频率附近的离子减少.

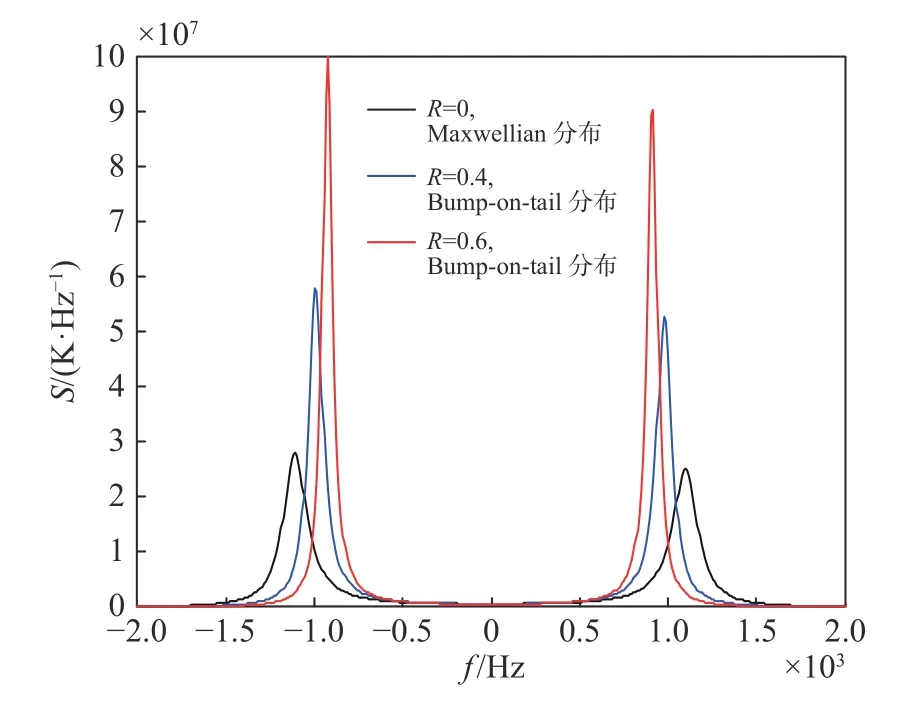
图6 vd=3 km/s时尘埃离子谱线随高能粒子组分的变化Fig. 6 The dust ion spectrum varies with the composition of high-energy particles, when vd=3 km/s

图7为尘埃离子谱线Bump-on-tail分布部分的非相干散射谱. 对比图6可以看出，当vd=3 km/s时Bump-on-tail分布离子产生的贡献小于整个尘埃离子谱线3个量级，故此时分布函数对谱线影响甚微. 这是由于尘埃组分的引入使得谐振频率发生变化，而在本仿真场景参数下，Bump-on-tail分布在谐振频率处的离子数量低于Maxwellian分布.

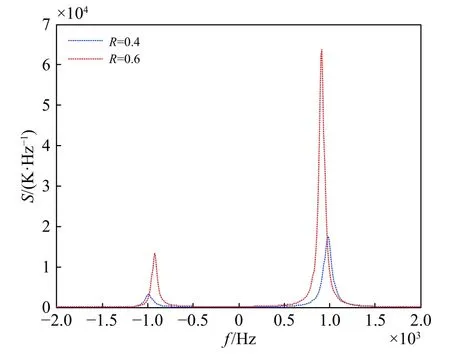
图7 vd=3 km/s时Bump-on-tail分布部分的尘埃离子谱线随高能粒子组分的变化Fig. 7 The dust ion spectrum of the bump-on-tail distribution varies with the composition of high-energy particles, when vd=3 km/s

图8为R=0.4时尘埃离子谱线随高能粒子速度的变化情况. 当尾向分布粒子漂移速度vd=0时(即Maxwellian分布时)，两个峰值相差不大. 当高能粒子速度增大到一定值时，非相干散射谱向某一特定的单峰结构逼近. 而后，随着速度的增大又恢复了双峰结构，但峰值高于Maxwellian分布，谱宽变窄.

图8 R=0.4时尘埃离子谱线随高能粒子速度的变化Fig. 8 The dust ion spectrum varies with the velocity of high-energy particles, when R=0.4

图9为R=0.4时Bump-on-tail分布部分的尘埃离子谱线. 可以看出：vd=1 km/s时Bump-on-tail分布部分的贡献最大；随着漂移速度的增大，贡献逐渐减小；当漂移离子速度为1～2 km/s时，尘埃离子出现谐振，且越靠近1 km/s，谐振越显著；当vd=3 km/s时，Bump-on-tail分布离子的贡献已不在107量级，解释了图6和图7中Bump-on-tail分布对仿真场景的非相干散射谱影响较小的现象.

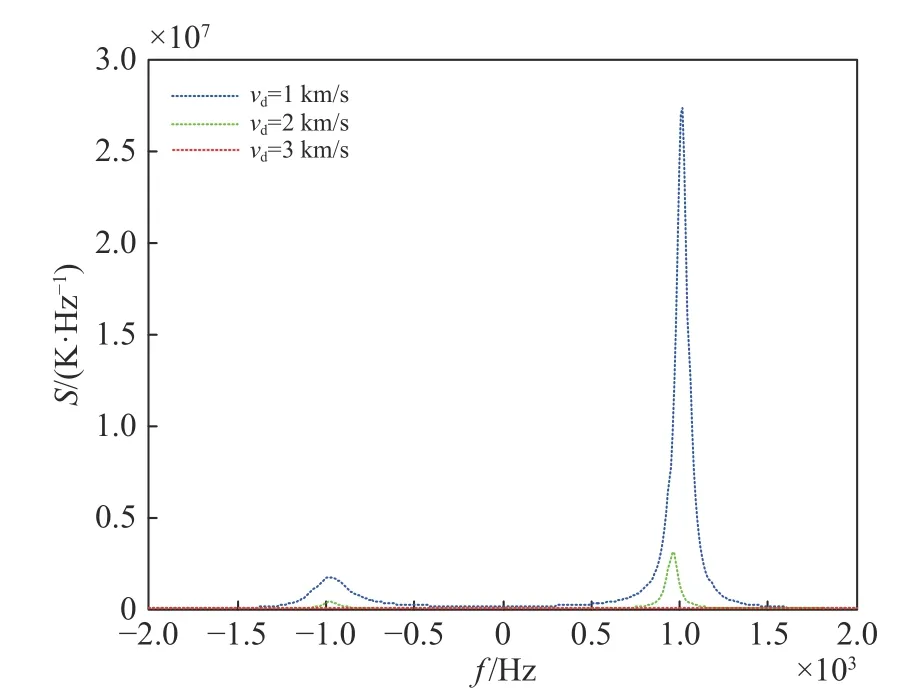
图9 R=0.4时 Bump-on-tail分布部分的尘埃离子谱线随高能粒子速度的变化Fig. 9 The dust ion spectrum of the bump-on-tail distribution varies with the velocity of high-energy particles, when R=0.4

3 结 论

文中基于尘埃等离子体非相干散射理论，建立了固体火箭喷焰早期离子Bump-on-tail分布的非相干散射模型，模拟并分析了尘埃掺杂和分布函数对非相干散射谱的影响，得出以下结论：

1)尘埃组分的引入增强了离子谱，拓宽了谱宽，这对所有场景参数具有普适性，有助我们对火箭尾焰的探测.

2)分布函数对离子谱线的影响则与生成的等离子体的离子谐振频率有着密切关系，当漂移速度使得Bump-on-tail部分的离子处于离子谐振频率附近时，分布函数的影响不容忽视. 在谐振频率附近，Bump-on-tail部分的离子量大于或等于Maxwellian分布在该谐振频率附近的离子量时，在整个等离子体的离子中占比少量的Bump-on-tail分布的离子和尘埃对整个谱线的贡献超过电子、Maxwellian分布的离子和尘埃的贡献，这对非相干散射反演理论提出了新的要求.

拾取离子的非平衡分布会影响ISR波，这种非平衡分布是在背景环境等离子体与尾气分子发生电荷交换时，且在这些离子重新组合之前产生的. 高速火箭喷焰产生的环形离子束在雷达散射谱中产生许多额外的谱线. 不仅是火箭喷焰的尾气中，在磁聚变装置和地球辐射带中发现的磁镜几何结构都具有损耗锥型分布，也可视为Bump-on-tail分布，在太阳风与地球磁层的弓形激波相互作用、彗星中性原子电离、太阳环与行星际磁场碰撞中均可产生. 故Bumpon-tail分布的研究对于理解空间等离子体和实验室等离子体的物理性质都具有重要意义.

火箭喷焰产生的环束离子分布通过两个过程影响ISR谱：1)离子速度的非均匀分布(Bump-on-tail分布)来改变散射效应；2)离子环分布会进一步驱动等离子体湍流不稳定性，激发低混杂波和离子声波对散射进行调制. 依据不同散射机制，建立更加完整的理论模型，进行短时间尺度非相干散射谱演化过程的仿真，寻找火箭发射的ISR观测机会并与实验观测进行对比验证是我们下一步所要完成的工作.