基于随机森林回归的煤矿瓦斯涌出量预测方法

吴奉亮， 霍源， 高佳南

(1.西安科技大学 安全科学与工程学院，陕西 西安 710054；2.西部矿井开采及灾害防治教育部重点实验室，陕西 西安 710054)

0 引言

瓦斯灾害事故是威胁煤矿安全高效开采的主要因素[1-2]，为遏制瓦斯事故的发生，准确、高效的煤矿瓦斯涌出量预测方法尤为重要[3]。由于煤矿瓦斯涌出量的各影响因子间呈现出非线性关系[4]，线性预测方法难以得到满意的预测结果。因此，灰色理论、神经网络和支持向量机等非线性映射方法被广泛应用于煤矿瓦斯涌出量预测。题正义等[5]基于模糊数学和灰色系统建立了瓦斯涌出量预测模型。李树刚等[6]将因子分析与BP神经网络相耦合，对瓦斯涌出量进行预测。付华等[7]提出了一种利用蚁群聚类算法优化Elman神经网络的瓦斯涌出量预测方法。孙林等[8]、董晓雷等[9]、张强等[10]利用支持向量机实现瓦斯涌出量预测；谢东海等[11]将未确知测度理论引入到瓦斯涌出量预测中。然而，煤矿瓦斯涌出量的影响因素众多且复杂，灰色理论往往不能满足预测精度要求；神经网络的预测精度依赖于样本容量，且存在训练速度慢、泛化能力差的问题；基于支持向量机的预测方法对超参数的选取有较高要求[12]。

随机森林算法具有参数少、学习速度快、适用于高维样本、可有效避免过拟合、预测精度高等优点[13-14]，已被广泛用于分类和回归问题。在煤炭瓦斯防治领域，随机森林算法已在瓦斯涌出量预测、煤与瓦斯突出预测等方面有所应用，如汪明等[15]建立了回采工作面瓦斯涌出量的随机森林预测模型。温廷新等[16]提出了一种将因子分析理论与随机森林算法相结合的煤与瓦斯突出等级预测方法。郑晓亮[17]将数据挖掘多重填补算法与随机森林算法相结合进行煤与瓦斯突出预测。本文在文献[15]的基础上，分析了特征变量的影响权重，优选出影响瓦斯涌出量的关键特征变量，建立随机森林回归模型，进行煤矿瓦斯涌出量预测，提高了预测精度和效率。

1 方法原理

1.1 基于随机森林回归的煤矿瓦斯涌出量预测

随机森林算法是以Bagging算法思想为基础建立的集成学习算法[18]，用于数据的分类和回归研究。该算法能够有效分析高维非线性数据，具有较好的泛化能力和预测性能[14]。随机森林算法用于研究连续变量的回归问题，称之为随机森林回归。

基于随机森林回归的煤矿瓦斯涌出量预测主要步骤如下[19]：

(1)采用bootstrap自助法重采样技术，在原始训练集中有放回地重复随机抽取n个与原始训练集样本容量相等的新训练样本数据集，未被采样选中的数据称为袋外数据。

(2)从影响煤矿瓦斯涌出量的M个输入特征中随机选择m个特征作为决策树分枝节点的备选特征变量集合，根据分枝优度准则，从集合中选取最优特征进行节点分裂，构建决策树。每棵瓦斯涌出量决策树自由完整地生长而不剪裁。

(3)构造出n颗瓦斯涌出量决策树，组成随机森林回归模型。取n颗决策树输出值的均值作为煤矿瓦斯涌出量预测结果，利用袋外数据(如残差平方均值)评价回归模型预测性能。

1.2 超参数寻优及特征变量重要性评估

随机森林回归模型的超参数包括决策树数目n和随机选用的特征个数m，其取值对回归模型的拟合和预测性能有重要影响[20]。若n值过小，会因回归模型训练不足而导致预测结果误差偏大；若n值过大，则会增加模型的计算量。若m值偏小，回归模型会因过拟合而导致预测精度降低；若m值偏大，则会降低模型运算速度。因此，构建随机森林回归模型时需对超参数n和m进行寻优。

对超参数n和m进行寻优时，首先设置超参数m值，回归分析中通常默认其值为输入特征变量数的1/3[21]，在m值不变的条件下，得到不同n值下袋外数据残差平方均值的变化情况。满足随机森林回归模型稳定性(残差平方均值随n值变化趋于稳定值)且模型训练效率较高时对应决策树数目n值为最优值。设n取最优值不变，计算不同m值下袋外数据残差平方均值和回归模型的拟合优度，选取残差平方均值小、拟合优度高的m值作为最优值。

在采用bootstrap自助法重采样形成随机森林回归模型训练集的过程中，每次采样约有36.8%的原始数据不会被取到，即袋外数据，它们将不参与回归模型训练，而是作为测试集对回归模型的泛化能力、预测性能和特征重要性进行评估[22]。

在随机森林回归模型中，通常是以特征变量的随机改变引起回归模型的变化程度来描述特征变量的重要性，具体是采用袋外数据残差平方均值的增加量(IncMSE)来表征特征变量的重要性，IncMSE越大，说明该特征变量对因变量越重要。对IncMSE进行归一化处理，得到各特征变量对因变量的影响权重[23]，本文用累计影响权重达到90%的部分特征变量代替煤矿瓦斯涌出量的全部特征变量，用于构建随机森林回归模型。

2 测试分析

2.1 样本数据

根据文献[7]，选用14个特征变量作为煤矿瓦斯涌出量预测模型的输入变量：煤层瓦斯含量X1，埋深X2，煤厚X3，煤层倾角X4，采煤高度X5，日进度X6，采煤工作面长度X7，采出率X8，邻近层瓦斯含量X9，邻近层厚度X10，邻近层间距X11，顶板管理方式X12，开采强度X13，层间岩性X14；输出变量：瓦斯涌出量Y。获取了20组原始数据，见表1。前16组原始数据用于训练回归模型，其余4组用于测试回归模型。

表1 随机森林回归模型训练和测试样本

2.2 超参数确定

设参数m的默认值为特征变量总数的1/3，煤矿瓦斯涌出量的影响因子有14个，因此，m=5。设决策树数目n为50，100，500，1 000，利用RStudio软件平台进行编程，建立随机森林回归模型，得到n取不同值时袋外数据残差平方均值，如图1所示。从图1可知，当n超过200后，袋外数据残差平方均值变化趋于平稳。综合考虑模型运算量和预测精度，取n为500。

图1 n取不同值时的袋外数据残差平方均值(14个特征变量)

取n=500固定不变，m取1～14(步长为1)，建立随机森林回归模型，得到m取不同值时模型的拟合优度与残差平方均值，如图2所示。从图2可知，m为7时对应拟合优度最大，残差平方均值最小，因此，确定最优值m=7。

图2 m取不同值时的拟合优度与残差平方均值(14个特征变量)

2.3 特征变量的选取

对IncMSE值进行归一化处理，得出各特征变量对煤矿瓦斯涌出量的影响权重及累计影响权重，如图3和图4所示。

图3 各特征变量重要性及影响权重

从图3可知，采煤高度、煤厚、煤层瓦斯含量、采出率、埋深、日进度、开采强度、邻近层间距等特征变量的影响权重较大，而邻近层瓦斯含量、倾角、采煤工作面长度、层间岩性、顶板管理方式、邻近层厚度等特征变量的影响权重相对较小。从图4可看出，采煤高度、煤厚、煤层瓦斯含量、采出率、埋深、日进度、开采强度、邻近层间距等特征变量的累计影响权重为91.10%，按照累计影响权重达到90%以上的关键特征变量选择规则，选取该8个特征变量作为影响煤矿瓦斯涌出量的主要因素。

图4 累计影响权重

2.4 预测结果对比

选取重要性排序前8的特征变量作为随机森林回归模型的输入变量，在保证训练样本相同的前提下，构建随机森林回归模型。首先进行超参数寻优，结果如图5和图6所示。

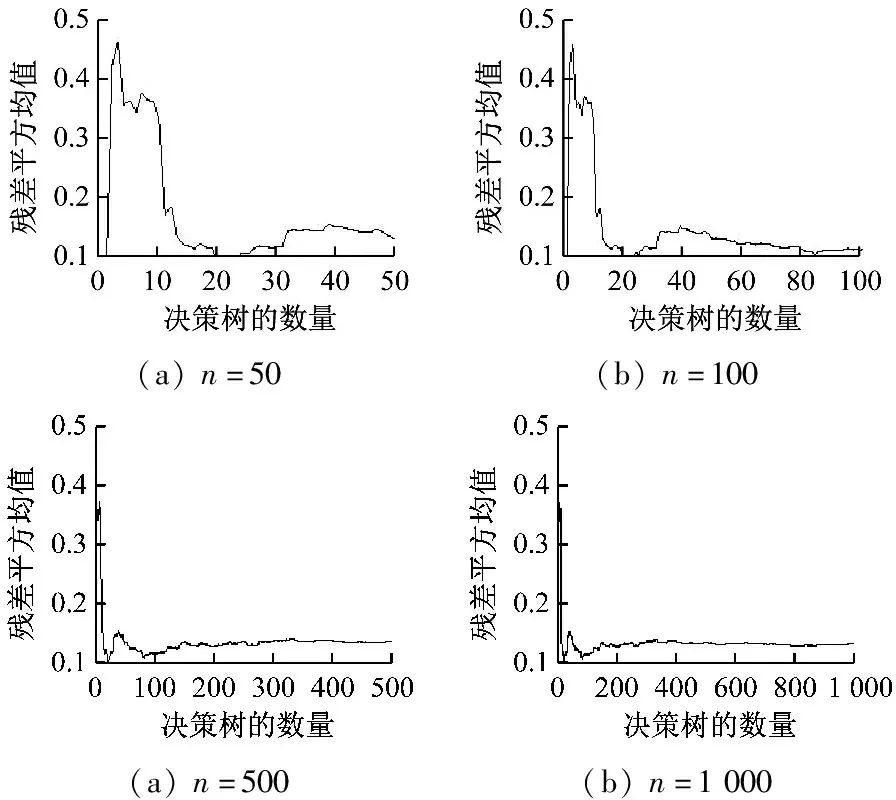
图5 n取不同值时的袋外数据残差平方均值(8个特征变量)

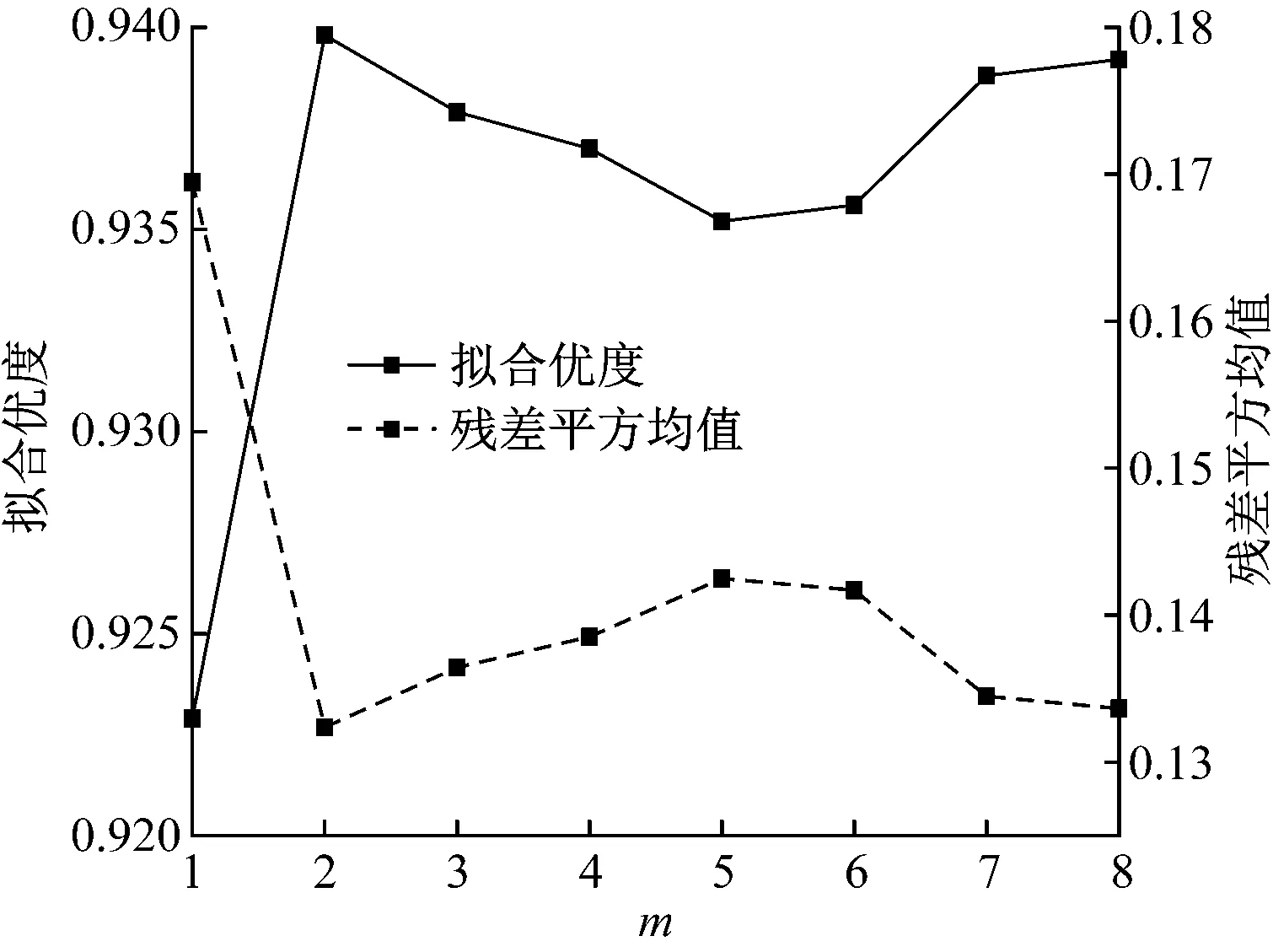
图6 m取不同值时的拟合优度与残差平方均值(8个特征变量)

从图5、图6可看出:n为500时，模型袋外数据残差平方均值变化平稳；m为2时，模型拟合优度最大，残差平方均值最小。因此，基于特征选择的随机森林回归模型的最优超参数为n=500，m=2。

为了评价基于特征变量选择的随机森林回归模型的预测性能，在保证预测样本相同的前提下，与全部14个特征变量参与的随机森林回归模型的预测结果进行对比，结果见表2。可看出，2种情况下随机森林回归模型均具有较好的预测性能，进行特征变量选择后，平均绝对误差由0.22 m3/min下降到0.21 m3/min，平均相对误差由3.55%下降到3.47%。基于特征变量选择的随机森林回归模型不仅能够保证较好的预测性能，而且降低了模型特征变量的维度，减少了原始数据获取工作，提高了预测效率。

表2 瓦斯涌出量预测误差对比

3 结论

(1)研究了基于随机森林回归的煤矿瓦斯涌出量预测方法。通过计算袋外数据残差平方均值和拟合优度，确定随机森林回归模型的最优超参数。

(2)通过特征变量重要性分析方法，从全部14个特征变量中优选出采煤高度、煤厚、煤层瓦斯含量、采出率、埋深、日进度、开采强度、邻近层间距8个关键的特征变量，建立特征选择后的随机森林预测模型。

(3)测试结果表明，采用全部特征变量和部分特征变量的随机森林回归模型均具有较好的拟合与预测效果。进行特征变量选择后，模型的平均绝对误差由0.22 m3/min下降到0.21 m3/min，平均相对误差由3.55%下降到3.47%。基于特征变量优选的随机森林回归模型保持了较高的预测精度，同时提高了模型预测效率，更加适用于煤矿瓦斯涌出量预测。