植被茎秆倾伏角变化对明渠水流结构的影响
刘明,张升堂,张景洲,赵庆星,孙桤汶,王磊
植被茎秆倾伏角变化对明渠水流结构的影响
刘明,张升堂*,张景洲,赵庆星,孙桤汶,王磊
(山东科技大学 地球科学与工程学院,山东 青岛 266590)
【】分析植被茎秆倾伏角变化对明渠水流结构流态的影响,充分发挥河道水生植被功能以减缓河堤的侵蚀和水土流失的速率。建立明渠植被水流结构模型将水流液层在空间高度上分为植被层和自由层,在茎秆不同的变形状态下及流量范围内开展试验。①在同一茎秆倾伏角下,植被层v随水深增加呈增加减少再增加最终趋于稳定的变化规律,自由层平均速度s、雷诺数s、弗劳德数s随水深的增大迅速减小后趋于稳定。②不同茎秆倾伏角下,植被层水力参数v、v、v在空间上表现出各向异性,自由层s、s、s随植被倾伏角增大而减小,植被淹没临界水深存在“滞后”现象。自由层的水流流速s、雷诺数s、弗劳德数s均大于植被层;植被层水流流态为缓紊流,自由层水流流态从急紊流迅速过渡到缓紊流。
倾伏角;植被层;自由层;流态
0 引言
【研究意义】全球洪涝灾害频发、水土流失加剧环境污染日趋严重威胁到人类生存,维护生态系统平衡至关重要[1-2]。水生植被作为河流生态系统的不可替代的一部分,一方面,水生植被不仅可为水生生物提供营养物质和生长环境,而且植被的根茎具有吸附固定作用抑制泥沙悬浮和改善水质;另一方面,植被可增加河道水流阻力、流速减缓以及水位升高,从而间接地控制河道泥沙输移、堤岸侵蚀、航运效率、水质净化及水环境等方面,所以植被是影响河道水流特性的关键因子[3-4]。因此研究河道植被水流流动变化规律在水土保持、稳定河堤及环境工程等领域具有重要意义。【研究进展】针对植被茎秆对明渠水流水力特性的研究,国内外研究者提出了明渠植被水流结构“分层理论”方法,在明渠植被水流中沿水深分为若干层以研究植被对水流水动力学特性的影响。Huai等[5]基于普朗特混合长度理论进行分析,通过三层水流结构模型预测明渠植被水流的垂向时均流速分布和紊流特性。王雯等[6]研究了刚性双层淹没植被水流特性,依据垂向流速的拐点划分为4个区域,在植被层的顶端雷诺应力和紊动能分布明显增强。Yang等[7]将双层水流结构模型运用于研究淹没植被明渠水流,假设植被层流速分布均匀以及自由层流速遵循对数分布,结果证实了实测数据和理论值高度吻合。Nepf等[8]分析淹没植被冠层顶部和内部水流紊动特性,冠层顶部产生的KH涡流控制垂直方向上动量交换,冠层内部的湍流动能与茎秆尺度相关。Li等[9]研究淹没植被的不同排列方式、间距以及密度对边界底层、植被层、非植被层水流结构的影响,结果表明时均流速在植被的顶部发生显著的变化。Yang等[10]采用塑料圆柱模拟河道刚性植被,并建立二维格点玻尔兹曼模型用来反应植被覆盖下河道水流流场分布。Liu等[11]通过多普勒测速仪测得高矮刚性植被组合水流流速在断面的分布特征。Tan等[12]通过水槽试验研究了刚性植被群对水流流速分布规律、紊动特性和消波效果的影响。【切入点】以往研究大多集中在探究刚性植被对水流断面点流速、雷诺应力等水力特性的影响,忽略了生长在河道中水生植被形态、种类、属性以及生长周期等特征并不相同,水生植被在河道中受到水流的冲击呈现不同程度的倾伏变形。【拟解决的关键问题】比较分析不同植被茎秆倾伏角下植被层、自由层水流水力特性的变化,研究不同植被茎秆倾伏角对明渠水流特性的影响。为河道输配水和水土保持提供理论指导。
1 试验设计与原理
试验在室内长5 m、宽0.4 m、高0.3 m的矩形明渠水槽中进行(图1),水槽从上游到下游依次分为上游平水段(1 m)、试验铺设段(3 m)、下游量水段(1 m),在水槽试验铺设段内设置2个断面,2个断面间隔1.5 m,且每个断面均设有测压玻璃管以观测断面水位的变化;试验铺设段底部放置有机玻璃板用来模拟河道水流的下垫面,有机玻璃板表面呈现相同孔径的钻孔,相邻钻孔纵横间距为60 mm×60 mm,在有机玻璃板的钻孔中放置铝棒以替代水生植被,圆柱铝棒长为10 mm、直径为4 mm,其与竖直面形成不同的夹角(图2)。水泵将自来水抽送至蜂窝处,水流经过电磁流量计和阀门,进入试验铺设段。流量和水深分别通过电磁流量计、测压玻璃管测量,电磁流量计的量程为0~0.018 m3/s,测压管记录断面1、断面2水深数据值,分别记作1、2,将断面1、断面2水深取平均值得到平均水深,利用水力学理论公式计算平均流速弗劳德数雷诺数等相关水力要素。为研究植被茎秆倾伏角变化对水流结构水力特性的影响,试验中采用控制变量法,即底坡与茎秆直径等,其他因素保持不变,仅通过改变茎秆的倾伏角进行量化分析。试验设置了4组茎秆倾伏角,分别为0°、20°、40°、60°,在坡度1%下开展试验(表1)。试验过程中记录流量水深以及试验现象。
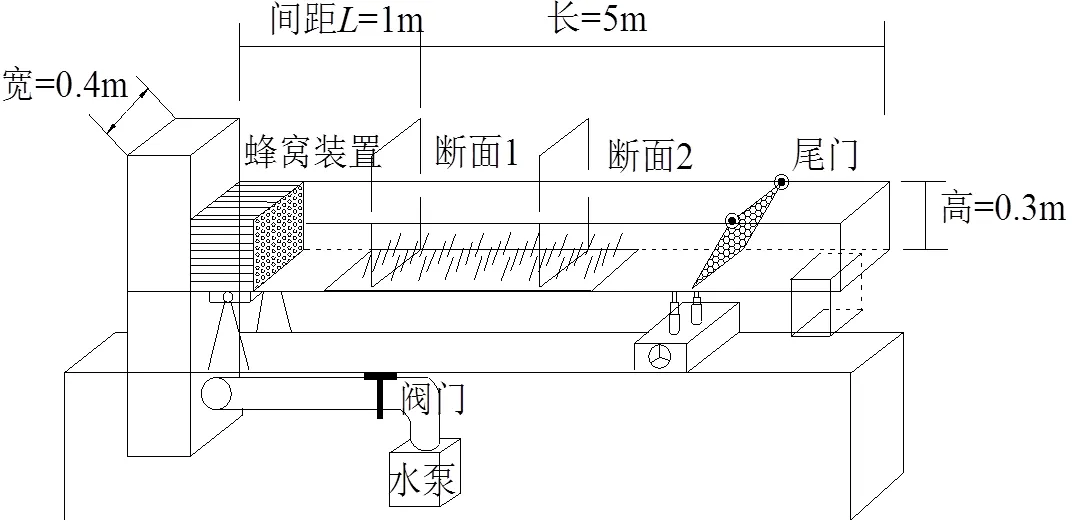
图1 试验装置
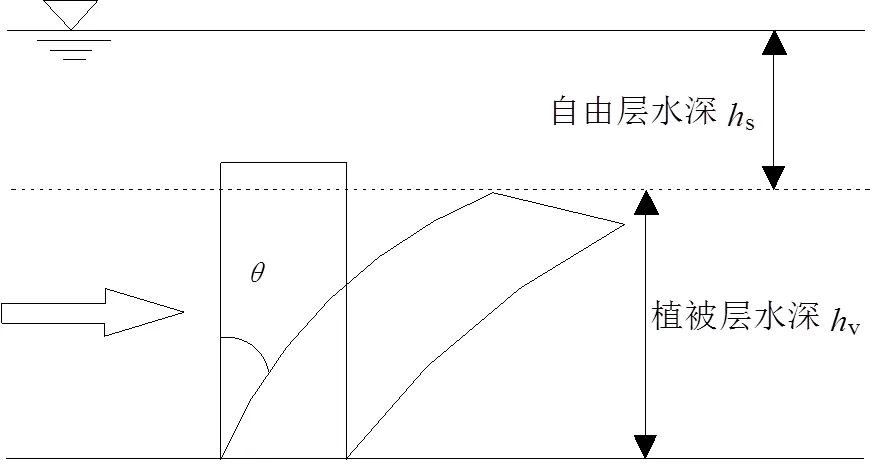
图2 植被变形下双层水流结构

表1 试验设置
在河道中阻碍水流流动因素众多,与其他因素相比,植被是制约水流流动的主导因素,并且由于植被自身内在的特征,如植被形态、属性和组合类型等特征在空间维度上对河道植被水流产生了重要影响,使得植被水力参数的计算变得复杂,为了简化相关水力参数的计算,将植被视作是均匀分布于河道下垫面的粗糙单元。大多数学者采用传统的一维达西-魏斯巴赫阻力公式分析,然而植被群作为一个大尺度的阻水体,在此情况下用达西-魏斯巴赫阻力系数及曼宁糙率系数量化含水植被阻水效果存在一些缺陷[13-14]。考虑到植被水流相关水力参数是由植被的茎秆与水流接触引起的,一些学者定义了新的相关水力参数以研究植被对水流流动的影响[15-17]。
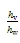
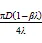
式中:为淹没度;表征植被垂直投影于下垫面的高度与水深之比;v为植被垂直投影于下垫面的高度;w为水深;v为植被相关的水力半径(m);为单位面积上模拟植被的密度;为植被的直径(mm);π取值为3.14。
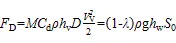
式中:D为植被阻力(kN);为下垫面单位面积上模拟植被数量(/m2);d为植被拖曳力系数;为水的密度(kg/m3);v为植被的高度(m);h为整体水深(m);v为明渠水流的平均速度(m/s);g为(9.8 m/s2);0为能坡(J/m),表征断面沿程能量损失的比降。
关于上述式中植被拖曳力系数的研究,通过查阅文献得到v~d的函数关系。Ergun[18]和Cheng[19]通过试验数据得到函数曲线。Cheng[19]分别进行了5种不同植被体积分数水流试验,结果表明同一植被体积分数水流条件下,d随v的增大呈先递减变化后趋于稳定。Zhang等[20]试验研究不同植被走向和坡度对拖曳力系数的影响,随着水深的增加拖曳力迅速减小后趋于稳定。Tanino等[21]研究了不同植被密度对拖曳力的影响,结果试验证明v~d关系与上述等研究结果相似。在非淹没状态下,d随的增加迅速减小后趋于稳定,当v大于某一值时,d变化幅度较小趋于稳定。Schlichting等[22]给出了不同雷诺数值下的植被水流拖曳力d值:
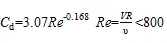
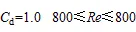
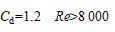
弗劳德数是用来判断水流流型的重要参数,表征动能与势能之比,植被层v定义为:
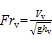
式中:v为植被层的弗劳德数;v为植被层的平均水流速度(m/s);g为重力加速度(9.8 m/s2);v为植被层水深(m/s)。
上述已经给出植被层水流相关水力参数的推导公式,依据过水断面总的流量等于植被层、自由层流量之和,可以解得到自由层其他相关水力参数s、s。

式中:e为植被层有效过水断面面积(m2);v为植被层平均水流速度(m/s);s为自由层过水断面面积(m2);s为自由层水流平均速度(m/s);下标“s”表征自由层相关的水力参数。
2 结果与分析
2.1 倾伏角θ及水深h对植被层平均流速Vv的影响
图3、图4、图5分别为植被变形作用下植被层水流平均速度v、雷诺数v、弗劳德数v、与水深的关系。由图3可知,当植被倾伏角保持不变时,植被层的水流v与水深呈倒“S”形分布[23]。水深在0~0.02 m范围内,水流v随着水深的增加呈显著上升的趋势,水流v切线斜率逐渐增大,此时水深是影响植被层水流v的主要因素;水深0.02~0.04 m时,随着明渠植被水深逐渐增加,同时植被与水流接触的横截面积增加,水流阻力增大,植被的“阻塞效应”大于水深增加对水流v贡献值,故植被层水流v与水深呈现负相关关系。水深大于0.04 m时,植被层水流v随水深的增加而增加后趋于稳定。可见,植被的存在使明渠水流产生植被绕流现象,植被的迎水面阻挡水流流动,水流液面雍高,液体层间的黏滞力使水体在植被变形周围分离,植被中间的雍水向二侧挤压,水流向植被之间的空隙流动,促使植被层水流v趋向均匀化[24]。
图3可以看出,由0°增加到60°时,植被层水流v表现为60°>40°>20°>0°,当植被倾伏角为60°时,植被与水流流向之间的夹角较小,顺于水流流向,对水流流速影响较弱;当倾伏角为0°时,植被相当于垂直下垫面的“小闸门”串联成一排,水流流经“小闸门”时,与“小闸门”发生强烈的正面碰撞,会产生较大的机械能损失,因此植被层水流流速受倾伏角的影响,可提高河道行洪能力和削弱堤岸侵蚀速率。
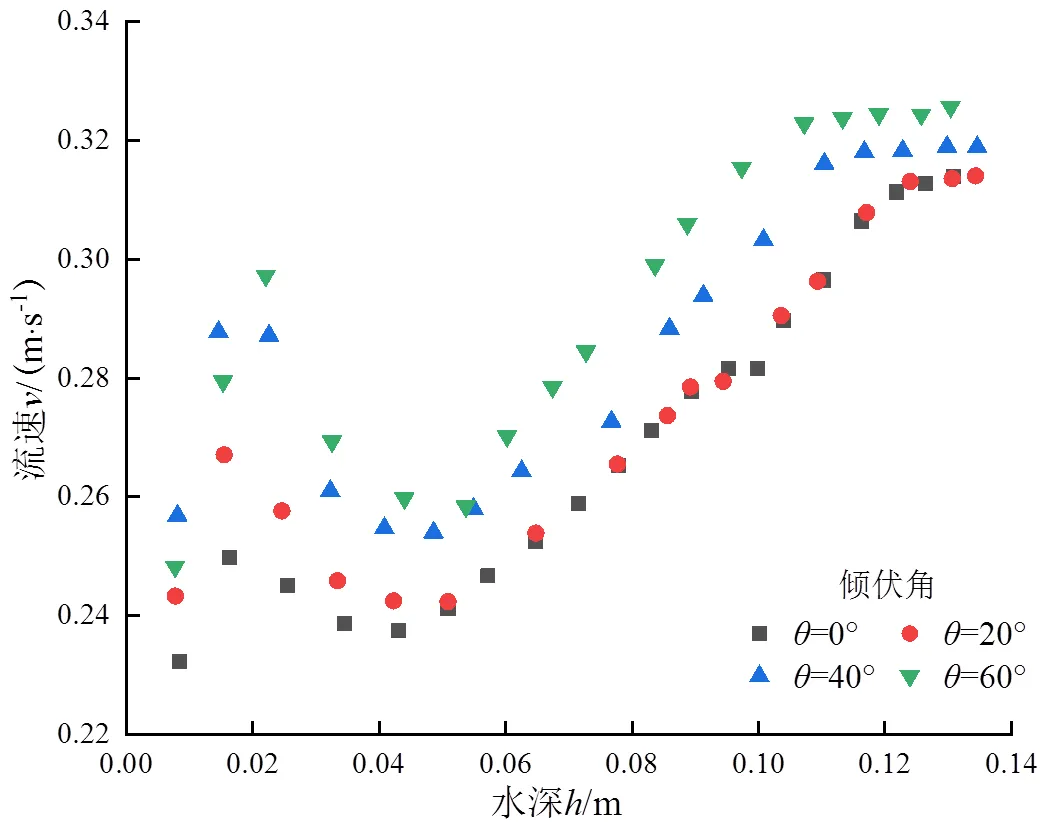
图3 植被层不同倾伏角下h~Vv关系曲线
2.2 倾伏角θ及水深h对植被层水流流态的影响
由图4可知,在~v关系曲线中,植被层雷诺数v变化区间(1 400~65 000),水流流态均为紊流。当试验植被恒定时,植被层v随着水深增加呈现线性增加的趋势。由于水深的增加,水体与植被粗糙单元接触的面积加大,植被的存在增加了对水流的扰动性。同一水深试验下,当水深大于0.04 m时,不同倾伏角的形态植被在水中,植被层水流v随增加而增加。因此,倾伏角是植被层水流v影响因子之一;当水深小于0.04 m时,不同倾伏角度下植被层水流雷诺数差异较小,液体层间的黏滞力及水槽边壁是影响雷诺数的主导因素。

图4 植被层不同倾伏角下h~Rev关系曲线
图5为植被层弗劳德数v与水深之间变化曲线。在不同植被倾伏角试验下,植被层水流弗劳德数v变化区间为(0.29~0.92),水流流型均为缓流。同一倾伏角下,随水深的增大呈先减小后趋于稳定,随着植被层水深增加,水流v大体呈增加的趋势,但是速度的增长速率逐渐减小,而水深增加的效果凸显出优势,水流的重力势能增加,故植被层v随水深增加呈显著减小的趋势。当明渠水流整体水深继续增加,淹没状态下植被层水深保持不变,水流流速趋于稳定,植被层水流v随水深增加呈不变趋势;同一水深不同植被倾伏角试验下,植被层v随增大而增大。
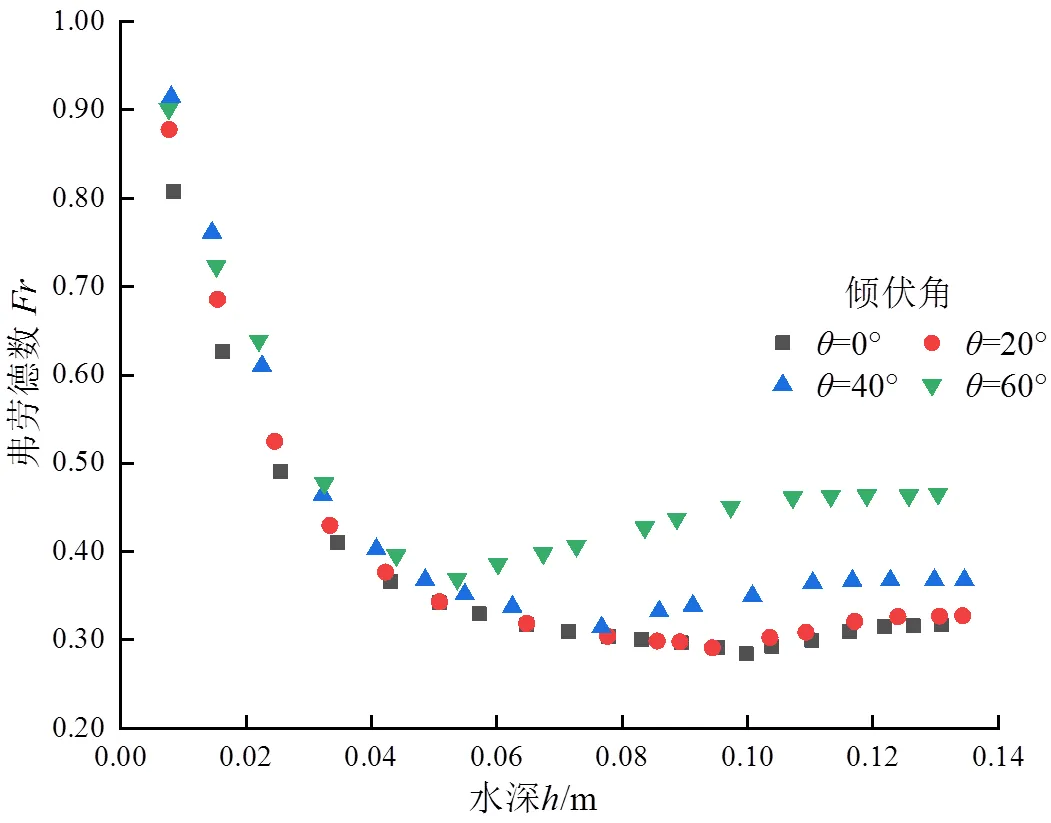
图5 植被层不同倾伏角下h~Frv关系曲线
2.3 倾伏角θ及水深h对自由层平均流速Vs的影响
图6、图7分别为自由层流速s与水深关系曲线图和流态流型分区。从图6可以看出,相同倾伏角条件下,如在60°植被倾伏角~s曲线中,随着水深的增加,自由层的平均水流流速先急剧下降后趋于稳定。植被初始淹没状态下,植被层和自由层的液面之间发生密切的水力,水力要素急剧变化,水流紊动增强,自由层水流s迅速减小。同一水深不同植被试验下,植被倾伏角越大,其对应植被淹没临界水深值越小,不同倾伏角下植被淹没临界水深值出现“滞后”现象,自由层平均流速s随倾伏角的增大逐渐减小。
2.4 倾伏角θ及水深h对自由层流态的影响
图7为不同倾伏角下自由层流态分区。自由层水流流态划分为6个区:缓层流、缓过渡流、缓紊流、急层流、急过渡流、急紊流。不同植被下自由层水流流速数据点大部分落在缓紊流区,仅在淹没临界水深附近处,少数试验点分布于急紊区,其他4个区均未分布。受下层植被顶部扰动的影响,水流紊动加剧。不同植被倾伏角下自由层值s及s存在差异,同一倾伏角工况下,s及s随水深增加迅速减小后趋于稳定。由于自由层水流惯性力减弱且重力势能增加,水流流态从急紊流迅速过渡到缓紊流,削弱了对河岸的侵蚀力度。
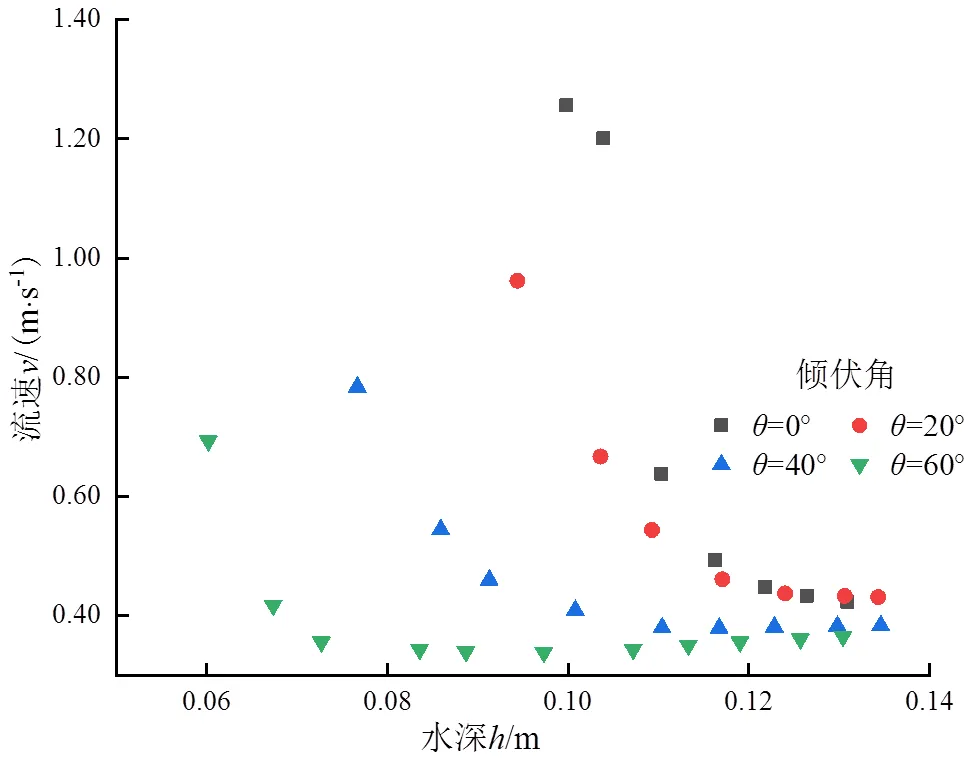
图6 自由层不同倾伏角下的h~Vs关系曲线
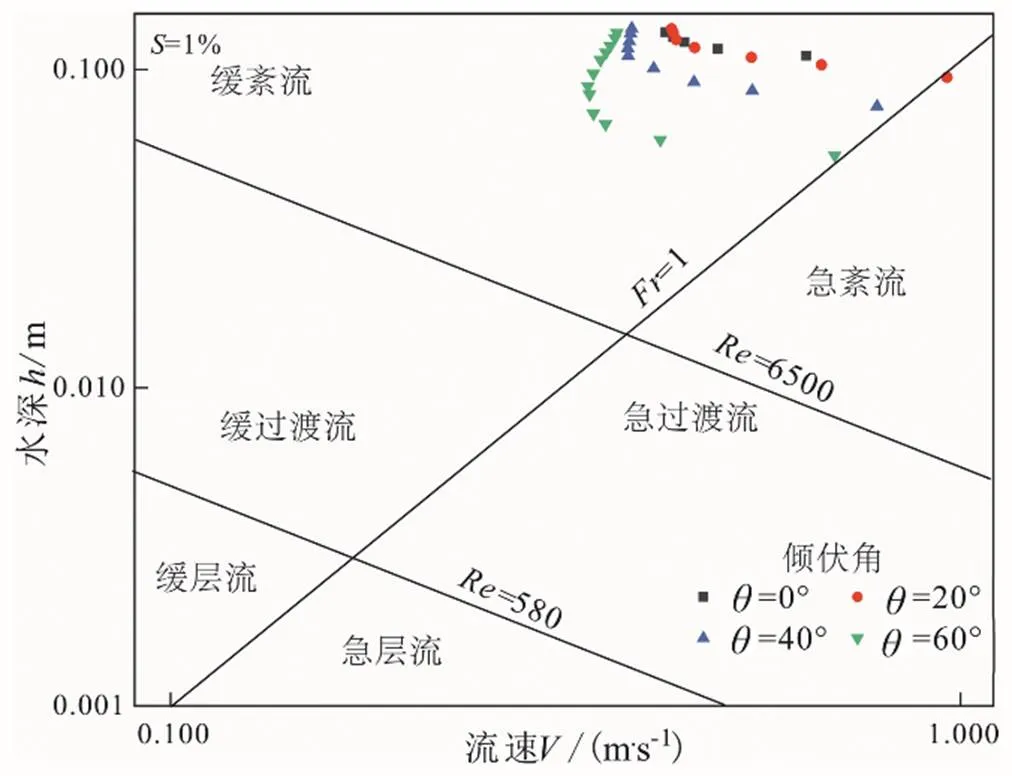
图7 自由层不同倾伏角下流态分区图
3 讨论
张景洲等[25]研究了植被的不同排列方式对坡面糙率及水流特性的影响,采用塑料棒模拟陆地植被与水流呈不同走向角,且植被垂直于水槽底板,结果表明相同水深工况下,植被走向角越小,植被茎秆与水流的接触面积越大,相应的水流阻力系数越大,流速越小。这与本试验不一致,考虑植被茎秆倾伏角的变化对明渠水流特性的影响,相同水深情况下,茎秆倾伏角越小,其茎秆的固液接触面积愈小,水流阻力愈小,水流流速越小。究其原因为:植被水流流速受主要因素影响即水流阻力和茎秆与水流碰撞动能的损失,茎秆倾伏角越小,水流阻力越小,倾伏角小的茎秆与水流发生正面碰撞损失的动能较多,故本试验植被层的平均流速随着茎秆倾伏角增大而增大。自由层的水流受茎秆倾伏角的影响,淹没临界水深值出现“滞后”现象,在淹没临界水深处,自由层的平均流速受植被顶端的扰动,水流流速迅速减小。随着水深的增加,不同倾伏角下自由层的流速趋于某一值。
本试验未从微观断面点流速进行探讨,在茎秆倾伏角的变化下,断面点流速以及水质点剧烈掺混引起的附加应力如何变化有待进一步开展试验研究。
本试验在室内开展,受某些因素的制约,比如试验水槽的宽度、坡度以及坡长等因素。即使试验是在等比例尺水力模型下进行,但仍和实际自然情况有差距。实际自然条件的坡度较陡,植被段的宽度较大。因此试验有待继续进一步优化探索。
4 结论
采用“分层理论”方法,将水流液层在空间高度上分为植被层和自由层,植被茎秆倾伏角变化对植被层、自由层水力特性影响如下:
①植被层:不同茎秆倾伏角下,植被层v、v、v与倾伏角均正相关,倾伏角越大,动能损失越小,对应的植被层流速越大,水流流态均为缓紊流,植被层水流流速受倾伏角的影响较大。
②自由层:不同茎秆倾伏角下,自由层s、s、s随倾伏角的增大而减少,水流流态从急紊流迅速过渡到缓紊流,水深淹没临界值出现“滞后”现象;随着水深进一步增加,茎秆的倾伏角变化对自由层水流影响减弱。
[1] DEWAN T H. Societal impacts and vulnerability to floods in Bangladesh and Nepal[J]. Weather and Climate Extremes, 2015, 7: 36-42.
[2] 史志华, 杨洁, 李忠武, 等. 南方红壤低山丘陵区水土流失综合治理[J]. 水土保持学报, 2018, 32(1): 6-9.
SHI Zhihua, YANG Jie, LI Zhongwu, et al. Soil conservation in the hilly red soil region of Southern China[J]. Journal of Soil and Water Conservation, 2018, 32(1): 6-9.
[3] 王子建, 丁雪, 吉庆丰. 含刚性沉水植物明渠水流结构的试验研究[J]. 灌溉排水学报, 2020, 39(2): 78-83.
WANG Zijian, DING Xue, JI Qingfeng. Experimental study on flow structure of open channels with rigid submerged plants[J]. Journal of Irrigation and Drainage, 2020, 39(2): 78-83.
[4] FRINGS R M, DÖRING R, BECKHAUSEN C, et al. Fluvial sediment budget of a modern, restrained river: The lower reach of the Rhine in Germany[J]. Catena, 2014, 122: 91-102.
[5] HUAI W X, CHEN Z B, HAN J, et al. Mathematical model for the flow with submerged and emerged rigid vegetation[J]. Journal of Hydrodynamics, Ser B, 2009, 21(5): 722-729.
[6] 王雯, 槐文信. 刚性淹没双层植被明渠水流紊流特性研究[J]. 四川大学学报(工程科学版), 2014, 46(1): 61-67.
WANG Wen, HUAI Wenxin. Turbulence structure of open channel flow through double layer rigid submerged vegetation[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 46(1): 61-67.
[7] YANG W, CHOI S U. A two-layer approach for depth-limited open-channel flows with submerged vegetation[J]. Journal of Hydraulic Research, 2010, 48(4): 466-475.
[8] NEPF H, GHISALBERTI M. Flow and transport in channels with submerged vegetation[J]. Acta Geophysica, 2008, 56(3): 753-777.
[9] CHEN S C, KUO Y M, LI Y H. Flow characteristics within different configurations of submerged flexible vegetation[J]. Journal of Hydrology, 2011, 398(1/2): 124-134.
[10] YANG Z H, BAI F P, HUAI W X, et al. Modelling open-channel flow with rigid vegetation based on two-dimensional shallow water equations using the lattice Boltzmann method[J]. Ecological Engineering, 2017, 106: 75-81.
[11] LIU D, DIPLAS P, HODGES C C, et al. Hydrodynamics of flow through double layer rigid vegetation[J]. Geomorphology, 2010, 116(3/4): 286-296.
[12] TAN C, HUANG B S, LIU D, et al. Effect of mimic vegetation with different stiffness on regular wave propagation and turbulence[J]. Water, 2019, 11(1): 109.
[13] FATHI-MOGHADAM M, KASHEFIPOUR M, EBRAHIMI N, et al. Physical and numerical modeling of submerged vegetation roughness in rivers and flood Plains[J]. Journal of Hydrologic Engineering, 2011, 16(11): 858-864.
[14] BANERJEE S, NAIK B, SINGH P, et al. Flow resistance in gravel bed open channel flows case: Intense transport condition[J]. ISH Journal of Hydraulic Engineering, 2019, 25(3): 298-309.
[15] CHENG N S, NGUYEN H T. Hydraulic radius for evaluating resistance induced by simulated emergent vegetation in open-channel flows[J]. Journal of Hydraulic Engineering, 2011, 137(9): 995-1 004.
[16] D’IPPOLITO A, LAURIA A, ALFONSI G, et al. Investigation of flow resistance exerted by rigid emergent vegetation in open channel[J]. Acta Geophysica, 2019, 67(3): 971-986.
[17] KOTHYARI U C, HAYASHI K, HASHIMOTO H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows[J]. Journal of Hydraulic Research, 2009, 47(6): 691-699.
[18] ERGUN S. Fluid flow through packed columns[J]. Journal of Materials Science and Chemical Engineering, 1952, 48(2): 89-94.
[19] CHENG N S. Calculation of drag coefficient for arrays of emergent circular cylinders with pseudofluid model[J]. Journal of Hydraulic Engineering, 2013, 139(6): 602-611.
[20] ZHANG S T, LIU Y C, ZHANG J Z, et al. Study of the impact of vegetation direction and slope on drag coefficient[J]. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2018, 42(4): 381-390.
[21] TANINO Y, NEPF H M. Closure to “laboratory investigation of mean drag in a random array of rigid, emergent cylinders” by yukie tanino and heidi M. nepf[J]. Journal of Hydraulic Engineering, 2009, 135(8): 693-694.
[22] SCHLICHTING B H, KESTIN T B J. Boundary-layer theory[J]. Fluid Mechanics, 1990, 20(1): 48-89.
[23] STOESSER T, KIM S J, DIPLAS P. Turbulent flow through idealized emergent vegetation[J]. Journal of Hydraulic Engineering, 2010, 136(12): 1 003-1 017.
[24] MAYAUD J R, WIGGS G F S, BAILEY R M. Characterizing turbulent wind flow around dryland vegetation[J]. Earth Surface Processes and Landforms, 2016, 41(10): 1 421-1 436.
[25] 张景洲, 张升堂, 刘元臣, 等. 植被排列方式对坡面糙率系数的影响研究[J]. 人民黄河, 2017, 39(5): 93-96, 111.
ZHANG Jingzhou, ZHANG Shengtang, LIU Yuanchen, et al. Studyon impact of vegetation arrangement on slope surface roughness coefficient[J]. Yellow River, 2017, 39(5): 93-96, 111.
The Effects of Plant Stem Inclination on Water Flow in Open Channel
LIU Ming, ZHANG Shengtang*, ZHANG Jingzhou, ZHAO Qingxing, SUN Qiwen, WANG Lei
( College of Earth Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China)
【】Most open channels are planted with vegetation to avoid erosion of channel beds and slopes while in the meantime facilitating decontamination of organic and inorganic pollutants in the water. However, the vegetation could detrimentally affect water flow. How the depth and growing direction of the vegetation affect water flow across the channel is an issue not well understood. The objective of this paper is to plug this gap.【】A physical model was established to simulate water flow in open channel with the vegetation taken into account. Water in the channel was divided into two layers: A vegetation layer and an overlaid free layer. The impact of the growing direction of the vegetation, characterized by their stem inclination angle, was studied experimentally.【】①When the inclination angle of the stems was the same, the water velocity in the vegetation layer,v, tended to level off as the water depth in the channel,, increased. In the free layer, the average velocity,s, the Reynolds numbers, Froude numbersincreased asymptotically asincreased. ②We found thatv,Reandvin the vegetation layer were spatially anisotropic varying with the stem inclination angle, while in the free layers,sandsdecreased as the stem inclination angle increased. There was a delay in the critical water depth above which the vegetation was submerged. 【】Water velocitys,sandsin the free layer were higher than that in the vegetation layer. Water flow in the vegetation layer was slow and turbulent, while in the free layer the water flow was rapid, in a transition from fast turbulence to slow turbulence. Our results can help open channel design on how to reduce erosion of its bed and slope by growing vegetation without risking flooding.
pitching angle; vegetation layer; free water flowing layer; water flow regime
TV14
A
10.13522/j.cnki.ggps.2020523
1672 – 3317(2021)08 - 0088 - 06
刘明, 张升堂, 张景洲, 等. 植被茎秆倾伏角变化对明渠水流结构的影响[J]. 灌溉排水学报, 2021, 40(8): 88-92, 128.
LIU Ming, ZHANG Shengtang, ZHANG Jingzhou, et al.The Effects of Plant Stem Inclination on Water Flow in Open Channel[J]. Journal of Irrigation and Drainage, 2021, 40(8): 88-92, 128.
2020-09-18
国家自然科学基金项目(41471025);山东科技大学研究生科技创新项目(SDKDYC180320)
刘明(1994-),男。硕士研究生,主要从事水文水资源方面研究。E-mail: lm0029@126.com
张升堂(1970-),男。教授,主要从事水文水资源方面研究。E-mail: zst0077@163.com
责任编辑:白芳芳

