共线改进的色玻璃凝聚理论中矢量介子产生研究
向文昌,蔡燕兵*,周代翠
(1.贵州财经大学金融物理重点实验室,贵阳 550025;2.华中师范大学粒子物理研究所,武汉 430079)
微扰量子色动力学预言强子内的胶子密度随着能量的增大而快速增加.当能量足够高时,胶子的密度将达到饱和状态,从而形成一种新的物质形态,人们称之为色玻璃凝聚态(color glass condensate,CGC)[1].色玻璃凝聚物质的快度演化满足Balitsky-JIMWLK 方程[2-4],此方程是一个无穷阶的级联方程,因此很难用于唯象研究.在平均场近似下,Balitsky-JIMWLK方程可以简化为闭合的领头阶Balitsky-Kovchegov (LOBK)演化方程[2,5],LOBK方程极大的方便了理论计算与实验数据的比较.LOBK 方程在描述偶极子与靶发生散射时,假定靶快度保持不变,认为快度演化发生在偶极子中,这一参考系极大地简化了LOBK方程的推导过程.
从LOBK 方程可以导出偶极子-靶发生深度非弹性散射(DIS)时的散射振幅满足几何标度行为,即偶极子散射振幅由两个独立变量r和Qs(x)的函数变为一个联合变量rQs(x)的函数,这里r和Qs(x)分别表示偶极子的横向大小和胶子饱和动量,x为Bjorken变量.基于色玻璃凝聚理论,Golec-Biernat 等人的研究发现在小x区域中电子—质子DIS总截面满足几何标度行为[6],该发现为色玻璃凝聚理论的有效性提供了一个强有力的支持.然而,Caola等人的研究发现在DGLAP演化理论框架下,电子—质子DIS总截面也表现出几何标度行为[7].因此,人们很难判断初始部分子系统的快度演化是服从CGC还是DGLAP演化规律.此外,当采用LOBK方程描述质子结构函数(F2)和高能重离子碰撞中末态粒子多重数分布时,都发现LOBK给出的散射振幅随快度的演化速度过快,从而导致领头阶的偶极子散射振幅只能定性的描述实验数据,而无法定量的解释实验数据[8].
在过去的二十年中,大量的研究致力于寻找初态部分子系统服从CGC演化规律的证据和计算次领头阶效应对BK方程的修正[9-11].在理论研究方面,首先通过重求和所有αsNc阶的贡献,考虑跑动耦合常数效应对Balitsky-JIMWLK方程的修正,得到一个跑动耦合常数修正的偶极子散射振幅快度演化方程(rcBK方程)[12],这里αs和Nc分别代表跑动耦合常数和夸克的色数.相对于LOBK演化方程,rcBK方程与LOBK方程在形式上保持一致,但是其演化核被跑动耦合常数效应修改了,从而使得偶极子散射振幅随快度的演化速度被压低.该压低效应(跑动耦合常数效应)有效的改善了色玻璃凝聚理论对质子结构函数的描述[8].从费曼图看,跑动耦合常数效应只考虑了夸克圈的贡献,仅属于其中一种次领头阶贡献.除了夸克圈之外,胶子圈的贡献也属于次领头阶效应.在rcBK方程推导出来后不久,Balitsky和Chirilli同时考虑了夸克圈和胶子圈的贡献,得到了完整次领头阶BK演化方程[9].但是数值解该次领头阶方程时发现,其给出的偶极子散射振幅随能量的增加可能出现负值,并且偶极子散射振幅对初始条件有很强的依赖关系,这些结果都不具有物理意义.通过追踪完整次领头阶演化方程的演化核发现,负值来自于演化核中的双对数项.为了解决该困难,需要对双对数项进行重求和.Buef等人采用运动学限制条件,推导了非局域的偶极子演化方程,试图解决完整次领头阶方程不稳定问题[13];Iancu等人提出了一套新颖的方法对共线对数项进行重求和,推导了共线改进的BK演化方程(ciBK方程)[14].从共线重求和看,非局域演化方程和ciBK方程具有等效性,它们都能有效的解决完整次领头阶方程不稳定的问题.此外,ciBK方程能较好的描述HERA能区电子—质子散射中质子的结构函数实验数据.
虽然ciBK在描述实验数据时取得了一定的成功,但是它的演化变量为射弹的快度(Y).最近的研究发现实验上测量质子结构函数等物理量时,通常采用靶快度作为演化变量(η),而以上提到的所有演化方程都是以射弹的快度作为演化变量,因此只能近似的用来描述实验数据.一个有效的做法是把以上提到的演化方程转换为以靶快度为演化变量的方程,使得其导出的偶极子散射振幅能直接用于描述HERA等实验上测量的数据[11,15-16].近来,Iancu等人基于LOBK方程,采用快度平移变换Y=η+ρ,并考虑到胶子辐射需满足时序效应的条件,即母胶子的寿命应大于子胶子的寿命,推导了共线改进的Balitsky-Kovchegov演化方程(BK-η)[11],该方程的演化变量为靶快度η.当利用BK-η方程描述HERA实验数据时,研究结果表明其能很好的定量解释实验数据[17].该研究结果提供了又一个较好的佐证支持CGC理论的有效性.
大量的研究表明矢量介子的产生过程对胶子饱和物理十分的敏感,因此矢量介子的产生能为探测胶子饱和物理提供一种优越的方式[18-19].为了寻找更多的证据支持CGC理论的有效性,本文将利用BK-η方程研究HERA能区电子-质子散射中矢量介子的产生;采用Runge-Kutta 方法数值解BK-η方程,得出偶极子散射振幅的数值形式,结合矢量介子产生微分截面,拟合HERA能区J/ψ和φ介子产生实验数据.对于共线改进的BK-η方程,得到的χ2/d.o.f分别为0.996(J/ψ)、1.089(φ),由此表明共线改进的BK-η方程能很好的描述实验数据.本研究结果为色玻璃凝聚理论的有效性提供了进一步的理论支持.
1 矢量介子产生截面和偶极子演化方程
本部分将首先介绍偶极子模型中矢量介子的产生截面;然后回顾领头阶偶极子散射振幅演化方程和共线改进的偶极子散射振幅演化方程;最后介绍矢量介子波函数.
1.1 偶极子模型中矢量介子产生截面
根据偶极子模型,衍射γ*p→Vp过程通常可分为三个子过程,见图1.第一个子过程为虚光子通过量子涨落成为一个偶极子,其由一对正反夸克组成.第二个子过程为偶极子与靶通过交换胶子发生相互作用.该过程包含了强相互作用的重要信息,故为最重要的部分.最后一个子过程为出射正反夸克对重结合产生矢量介子.由此可知光子-质子衍射相互作用截面可以因子化成三个部分,即光子波函数、偶极子-质子散射振幅和矢量介子产生波函数.矢量介子产生的散射振幅虚部可以写为:
(1)
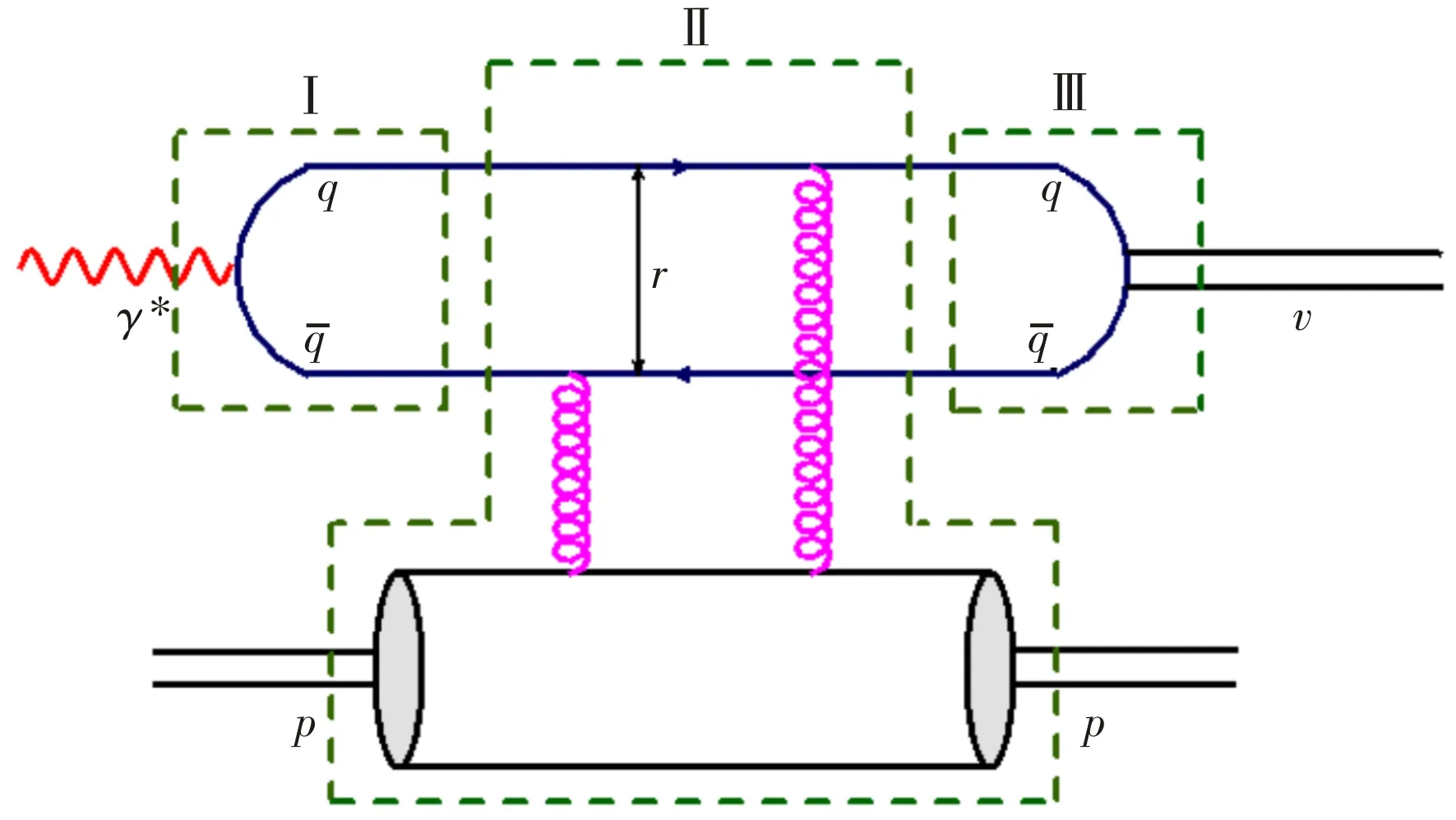
图1 偶极子模型中矢量介子产生过程Fig.1 Vector meson production in the dipole model
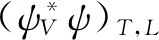
(2)
在方程(2)中,人们最关心的是偶极子散射截面dσdip/db,因为其包含了强相互作用的重要信息.根据光学定理,dσdip/db可以表示为偶极子-靶向前散射振幅的虚部:

(3)
其演化满足BK方程,下一小节将详细介绍LOBK方程和共线改进的BK-η方程.散射振幅对碰撞参数的依赖属于非微扰物理,很难直接计算.通常人们采用模型的形式引入散射振幅对碰撞参数的依赖.本研究将采用Marquet,Peschanski和Soyez(MPS)提出的碰撞参数依赖方案[18],他们假定散射振幅对碰撞参数的依赖关系具有高斯形式,并把散射振幅从b空间傅立叶变换到q空间:
(4)
把方程(3)和(4)代入(2)中,并经过简单的数学计算可得:
(5)
这里采用一种推广的形式给出[17]:
(6)
其中,因子e-Bq2来自于非微扰效应的贡献,R为质子的半径,N(r,x)为偶极子散射振幅.这里B和R为模型参数,可通过拟合HERA实验数据来确定它们的值.
利用衍射光子-质子散射振幅(5),可以得到矢量介子产生的微分散射截面为
(7)

(8)
这里δT,L写为
(9)
总微分散射截面将是横向(T)和纵向(L)微分散射截面之和.
1.2 偶极子散射振幅演化方程
为了得到方程(6)中的偶极子散射振幅,本小节将分别介绍描述偶极子随射弹快度和靶快度演化的方程,即LOBK方程和BK-η方程.

图2 偶极子随快度演化示意图Fig.2 Schematic diagram for the dipole rapidity evolution
在高能情况下,考虑一个由正反夸克组成的偶极子与靶(可能是一个强子或一个核)发生相互作用,其散射振幅满足LOBK方程[2,5]:
N(r,Y)-N(r1,Y)N(r2,Y)],
(10)
其中,Y为射弹的快度;KLO为演化核,其表达式为:
(11)

领头阶BK方程仅仅只对αsln(x)进行了所有阶重求和,并假定跑动耦合常数为一个固定值,因此该方程为一个领头阶方程.人们在采用LOBK方程描述HERA能区电子-质子深度非弹性散射中F2时发现,其给出的计算结果比实验数据大,表明该方程给出的偶极子散射振幅随快度的演化速度过快,所以只能定性的解释实验数据,而无法定量的描述实验数据.为了能定量的描述实验数据,需要在领头阶BK方程的基础上考虑高阶辐射修正.接下来介绍BK方程的共线修正,有时也称为双对数重求和效应.
众所周知,在理论上,为了简化高能偶极子与靶相互作用散射振幅的计算过程,BK演化方程是在靶静止系中推导的,认为所有的演化发生在偶极子(射弹)中.这一坐标系选取方法有效地避免了靶演化过程中的非线性效应.然而,在实验室测量时通常采用靶快度作为演化变量,如HERA能区ZEUS和H1实验在测量F2、σred等物理量时,使用靶快度η=ln(1/x),而非射弹快度Y.实验测量和理论计算之间出现了不匹配的演化变量.因此,所有基于BK理论的演化方程都需要从射弹快度表示变换到靶快度表示才能准确的描述HERA实验数据[8].最近关于质子结构函数的研究时发现采用η作为演化变量的BK方程能更好的描述F2实验数据[17].基于以上的成功经验,本文将采用共线改进的BK-η方程来研究矢量介子的产生.
为了得到BK-η方程,将基于LOBK方程,采用变量变换的方法,把射弹演化的BK方程变换到靶演化的方程.靶快度和射弹快度可以分别表示为:
(12)
(13)
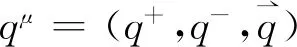
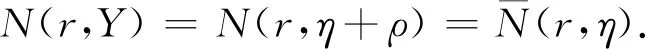
(14)
同理,
N(r1,Y)=N(r1,η+ρ)=
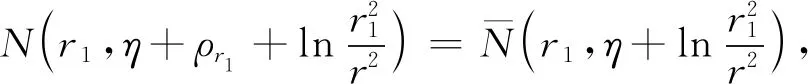
(15)
N(r2,Y)=N(r2,η+ρ)=
(16)
为了得到BK-η方程,首先需要把方程(15)和(16)进行展开
(17)
(18)
把方程(14)、(17)和(18)代入(10)中,并利用胶子辐射时需满足的时序条件,即母偶极子的寿命需大于子偶极子的寿命,可得共线改进的偶极子演化方程BK-η[11]:
(19)
其中,快度平移量
(20)
(21)
这里强调方程(19)已经是以靶快度作为演化变量的共线改进的BK方程,其可以直接用来描述ZEUS和H1实验数据.在下一节将采用数值方法解方程(10)和(19),得出数值形式的领头阶和共线改进的偶极子散射振幅,并结合矢量介子产生截面,拟合HERA实验数据,给出实验数据的理论解释.
1.3 矢量介子波函数
在计算矢量介子产生截面时,由方程(1)可知,光子与矢量介子的重叠波函数是其中重要的一部分.光子-矢量介子重叠波函数有几种不同的形式,如boosted Gaussian、Gauss-LC、DGKP[18-20].研究发现,不同的矢量介子对波函数的具体形式有一定的偏好性.由于本研究主要关注偶极子截面对矢量介子产生的影响,因此将只使用一种重叠波函数.横向和纵向的光子-矢量介子重叠波函数可以写为[20]:
[z2+(1-z)2]εK1(εr)∂rφT(r,z)},
(22)

(23)
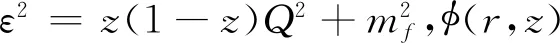
(24)
表1给出了方程(22)~(24)中MV、mf、NT,L和RT,L等参数的值.

表1 Boosted Gaussian标量函数中J/ψ和φ介子的参数[20]Tab.1 The parameters of boosted Gaussian scalar function for J/ψ and φ[20]
2 数值结果
本节首先将采用数值方法求解微分积分形式的演化方程(10)和(19),得到数值形式的偶极子散射振幅.然后把这些数值的偶极子散射振幅代入方程(5)和(7)中,计算HERA能区J/ψ和φ介子的微分散射截面和弹性散射截面.我们的研究结果将显示共线改进的色玻璃凝聚理论比领头阶色玻璃凝聚理论更好的描述实验数据.
2.1 偶极子散射振幅的数值解
偶极子散射振幅随快度的演化方程(10)和(19)是微分积分方程,它们的数值解需要初始条件.本文采用McLerran-Venugopalan模型作为初始条件[21]:
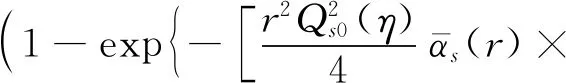
(25)
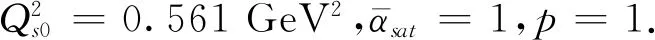
在网格上数值解演化方程(10)和(19),把偶极子平均地分离成512个离散点,并放在对数空间网格点上,r的取值范围从rmin=10-8GeV-1到rmax=50 GeV-1.为了简化计算,本研究假定偶极子散射振幅不依赖于碰撞参数,即N=N(|r|,η).采用GNU科学计算程序库(GSL)荣格-库塔方法求解微分方程,并使用辛普森算法计算方程中的积分运算[10,22].快度演化步长设为Δη=0.1,根据描述实验数据的需要,快度最大演化到η=20.此外,对于方程在演化过程中出现一些不在网格上的数值点,采用三次样条插值方法计算它们的值.
对于方程(19)和(25)中的跑到耦合常数αs(r),本研究采用一圈精度水平的跑动耦合常数方案,
(26)
其中,b=(11Nc-2Nf)/12π.为了防止红外发散行为,当r>rfr时,取αs(rfr)=0.75.
图3给出了4种不同快度情况下偶极子散射振幅随其横向大小的变化情况,实线代表BK-η方程的解,虚线代表LOBK方程的解,黑线、蓝色、红色和紫色分别代表快度为0、4、8和12的结果.从图3中可以看出共线改进的BK-η方程给出的偶极子散射振幅随快度的演化速度远小于LOBK方程的情况,该结果表明次领头阶效应对偶极子散射振幅的演化有较大的修正作用.在接下来的研究中将显示,正是由于次领头阶辐射修正带来的压低效应,使得理论计算能较好地描述实验数据.
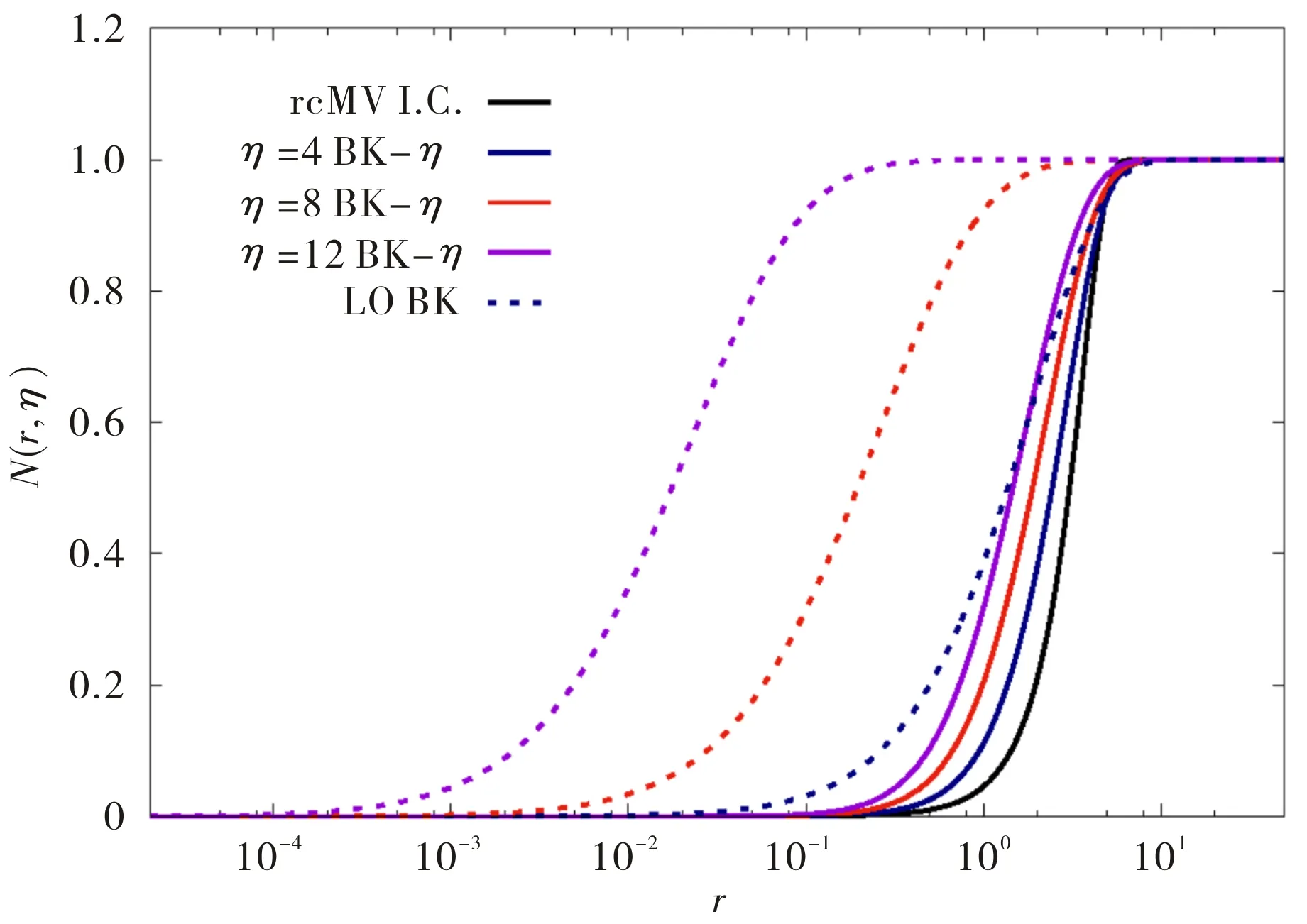
图3 不同快度时偶极子散射振幅的数值解Fig.3 The numerical solutions of the dipole scattering amplitude at different rapidities
2.2 HERA实验数据描述
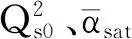
表2和3分别给出了J/ψ和φ介子的拟合参数和χ2/d.o.f,表中的第一列代表不同的偶极子散射振幅,其中LOBK和BK-η分别代表领头阶和共线改进的偶极子散射振幅.从表2和3中最后一列可知共线改进的演化方程(BK-η)给出的χ2/d.o.f比领头阶演化方程(LOBK)给出的值更接近于1,表明共线改进的演化方程较领头阶演化方程能更好的描述HERA的实验数据.当观察从拟合J/ψ和φ介子产生的实验数据得到的χ2/d.o.f时,发现共线改进的演化方程给出的结果较领头阶演化方程给出的值有很大的提高.这些结果说明次领头阶效应压低了偶极子随快度的演化速度,其在描述HERA数据中起着非常重要的作用.
图4给出了不同Q2时J/ψ和φ的微分散射截面随|t|变化情况.图的左边为J/ψ介子产生的微分截面,右边为φ介子产生的微分截面.图中的实
线代表采用共线改进的演化方程计算的结果,虚线代表采用领头阶演化方程计算的结果.从图中可以看出不论是J/ψ还是φ介子,共线改进的偶极子散射振幅比领头阶偶极子散射振幅能更好的描述实验数据.由图可知使用领头阶偶极子散射振幅计算得到的矢量介子微分截面普遍都大于采用共线改进的偶极子散射振幅计算的截面,这一结果与理论预期很好的相一致,即高阶效应(这里指共线改进效应)压低了偶极子散射振幅随快度的演化速度.同时,该结果也与表2和3给出的χ2/d.o.f相一致,即由BK-η拟合得到的χ2/d.o.f比LOBK方程得到的值更接近于1,表明次领头阶共线修正效应在描述HERA实验数据时有着重要的物理意义.

表2 J/ψ介子产生截面的拟合参数和χ2/d.o.fTab.2 The fitting parameters and χ2/d.o.f of the J/ψ production
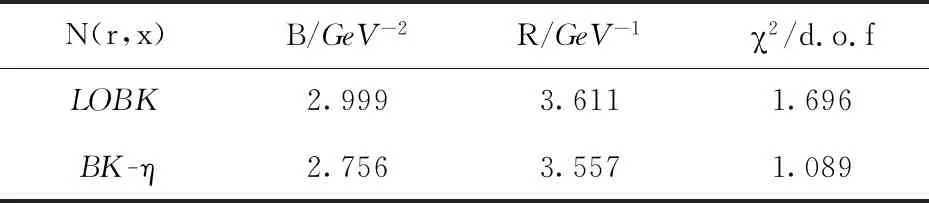
表3 φ介子产生截面的拟合参数和χ2/d.o.fTab.3 The fitting parameters and χ2/d.o.f of the φ production
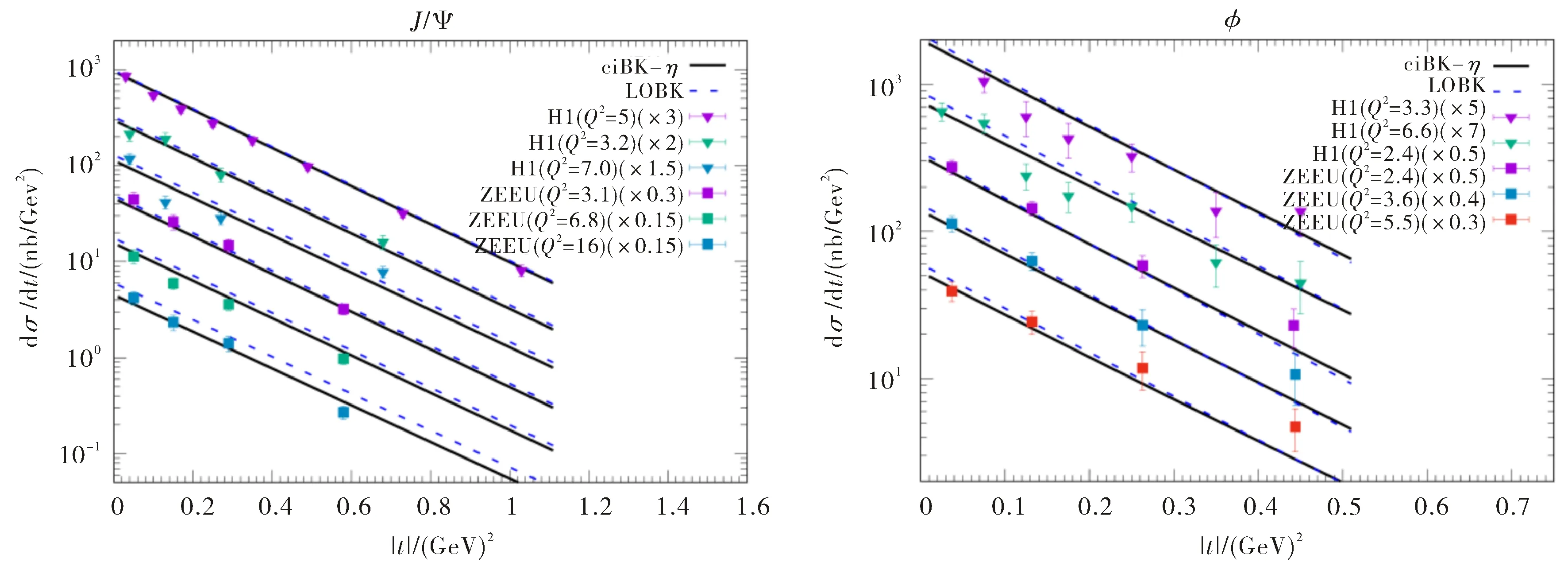
图4 不同Q2时J/ψ和φ介子产生的微分截面随|t|变化情况,数据来自于H1和ZEUS两个实验组[23-26]Fig.4 The differential cross sections of the J/ψ and φ meson productions as a function of |t|at different Q2.The data come from H1 and ZEUS collaborations[23-26]
图5给出了J/ψ和φ的弹性散射截面随Q2变化情况.左边和右边的图分别表示J/ψ和φ介子产生的弹性截面.图中实线代表由共线改进的演化方程计算的结果,虚线代表由领头阶演化方程计算的数值结果.从图5可以看出,由共线改进的演化方程计算得到的弹性散射截面理论值较领头阶演化方程的结果更接近于实验数据.此外从整体趋势来看,共线改进的演化方程所得计算结果更能描述实验数据,尤其是在大Q2区域,领头阶演化方程所得结果与实验相差较大.
为了进一步的说明共线修正效应的重要性,研究了J/ψ和φ的弹性散射截面随能量Wγ*p的变化情况,相关的结果显示在图6中.图中实线代表由共线改进的演化方程计算的结果,虚线代表由领头阶演化方程计算的数值结果.从图6可以看出,不论是J/ψ和φ介子,共线改进的演化方程给出的描述都较领头阶方程有较大的提高.此外,由图6还可以看出,在能量较大时领头阶演化方程给出的计算结果很大的偏离了实验数据值,这个现象可以从图3中找到相关原因.在图3中比较同一快度时共线改进的偶极子散射振幅和领头阶偶极子散射振幅,不难发现领头阶偶极子散射振幅的演化速度远远大于共线改进的散射振幅,而且随着快度的增加差别越来越大,从而引起在高能量区域弹性截面的理论计算值大于实验测量值.
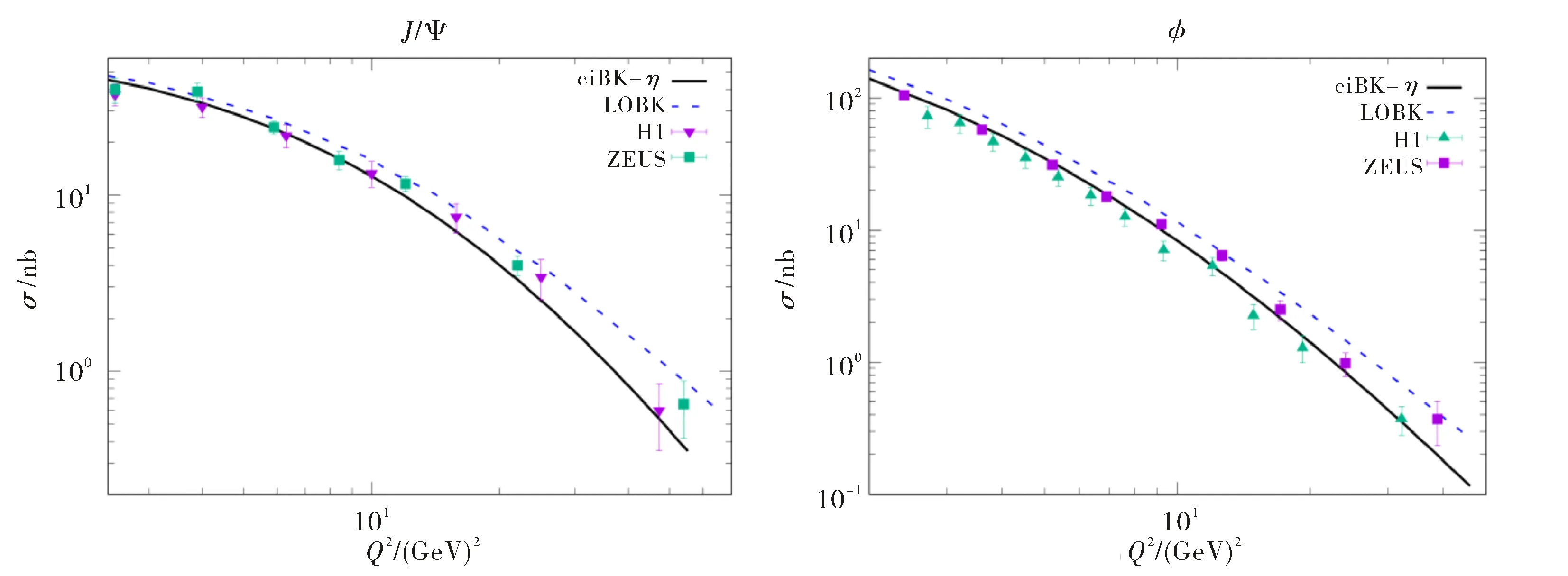
图5 J/ψ和φ介子产生的弹性散射截面随Q2变化情况,数据来自于H1和ZEUS两个实验组[23-26]Fig.5 The elastic cross sections of the J/ψ and φ meson productions as a function of Q2.The data comes from H1 and ZEUS collaborations[23-26]
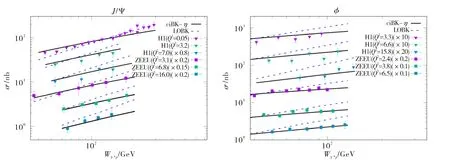
图6 不同Q2时J/ψ和φ介子产生的弹性散射截面随Wγ*p的变化情况,数据来自于H1和ZEUS两个实验组[23-26]Fig.6 The elastic cross sections of the J/ψ and φ meson productions as a function of Wγ*p at different Q2.The data comes from H1 and ZEUS collaborations[23-26]
3 总结与讨论
在色玻璃凝聚理论框架下,本文分别采用领头阶和共线改进的偶极子演化方程对J/ψ和φ介子的产生进行了深入的研究.在第二部分首先介绍了偶极子模型中矢量介子的产生公式,采用了MPS提出来的有效方法引入散射振幅对碰撞参数依赖关系,MPS 方法极大的方便了理论计算与实验数据的直接比较.在第二部分中还回顾了领头阶偶极子演化方程,并详细地介绍了以射弹快度为演化变量的方程转换成以靶快度为演化变量的推导过程.采用荣格-库塔方法分别数值求解领头阶和共线改进的演化方程,结果显示次领头阶的共线改进效应极大的压低了偶极子随快度的演化速度.利用偶极子散射振幅的数值解,结合矢量介子产生公式,拟合了HERA能区H1和ZEUS的实验数据,拟合结果显示由共线改进的演化方程计算得到的χ2/d.o.f比领头阶演化方程计算的值更接近1,由此表明共线改进的演化方程能更好的描述实验数据.由上可知,基于色玻璃凝聚的理论计算能很好的解释实验数据,这一研究结果为证明色玻璃凝聚的有效性提供了进一步理论支持.

