2-正规矩阵

张雨婷， 朱子建， 赵 瑞， 陆 彦， 魏俊潮

(扬州大学 数学科学学院，江苏 扬州225002)

1 引 言

A=AA+A，A+=A+AA+，AA+=(AA+)H，A+A=(A+A)H；

A=AA#A，A#=A#AA#，AA#=A#A.

一个n阶复方阵A是群可逆矩阵当且仅当rank(A)=rank(A2)；若群可逆矩阵A满足条件A#=A+，称为EP矩阵[3]；若AAH=AHA，则称A是正规矩阵[4]；若A2AH=AHA2，则称A为2-正规矩阵.显然正规矩阵是2-正规矩阵，但下面的注1说明2-正规矩阵不必为正规矩阵，因此2-正规矩阵是正规矩阵的真正推广.

矩阵广义逆的研究涉及众多科学领域，应用范围极其广泛，矩阵广义逆[5]形式众多，研究成果丰富，并逐渐影射到C*-代数[6]，Banach代数[7]，Hilbert空间中的线性算子广义逆[8]以及代数学的半群与结合环上的广义逆[9-10]，研究范围之广，研究学者之多，研究成果之巨使其成为广义逆理论中最耀眼的课题.本文主要是基于正规矩阵的良好性质，做出合理推广，介绍并研究了2-正规矩阵的相关性质.

2 主要结果

故A不是正规矩阵.

注1说明2-正规矩阵是正规矩阵的真正推广.

正规矩阵总是EP矩阵，从而为群可逆矩阵.但2-正规矩阵不必为群可逆矩阵，例如

由例1知，A为2-正规矩阵，但A不是群可逆矩阵，从而2-正规矩阵不必为EP矩阵.因此研究正规矩阵哪些性质遗传到2-正规矩阵上来就有着理论上的意义，同时研究2-正规矩阵的性质及其在对角化问题，特征值的性质等具有重要的理论价值.关于2-正规矩阵，首先有下面的结果.

引理1设A为2-正规矩阵，若A为群可逆矩阵，则A为EP矩阵.

证由于A为2-正规矩阵，则A2AH=AHA2，故

A2AHA+A=AHA2A+A=AHA2=A2AH，

又因为A为群可逆矩阵，所以

AAHA+A=A#A2AHA+A=A#A2AH=AAH，

从而

AHA+A=(A+AAH)A+A=A+(AAHA+A)=A+(AAH)=AH，

则

A=(AH)H=(AHA+A)H=A+A2，

所以AA#=A+A2A#=A+A，因此A为EP矩阵.

观察引理1的证明，实际上有下面的推论.

推论1设A∈n×n是群可逆矩阵，若存在正整数k，使得AkAH=AHAk，则A是EP矩阵.

下面的引理是众所周知的，给出了一种高等代数式的证明.

引理2设A∈n×n，若rank(A)=rank(A2)，则A为群可逆矩阵.

证设rank(A)=rank(A2)=r，则存在n阶可逆复方阵P和Q，使得

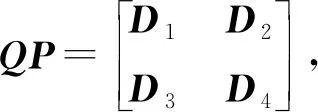
所以

故

因此rank(D1)=r，即D1为r阶可逆方阵.

故A为群可逆矩阵且

推论2设A∈n×n，若AH=AHA+A，则A为EP矩阵.

证由于AH=AHA+A，则

A=(AH)H=(AHA+A)H=A+A2，

所以rank(A)=rank(A2)，由引理2知A为群可逆矩阵，再由引理1的证明知A为EP矩阵.

类似于推论2，可得如下推论.

推论3设A∈n×n，若AH=AA+AH，则A为EP矩阵.

由于(AH)2A=A(AH)2当且仅当AHA2=A2AH，且一个群可逆矩阵A是EP矩阵当且仅当A#=A#AA+.因此得出下面的定理.

定理1设A∈n×n为群可逆矩阵，则A为2-正规矩阵当且仅当(AH)2A#=A#(AH)2.

证必要性.假设A为2-正规矩阵，则由引理1知A为EP矩阵，故

(AH)2A#=(AH)2A(A#)2=A(AH)2(A#)2=A#A2(AH)2(A#)2
=A#(AH)2A2(A#)2=A#(AH)2AA#=A#(AH)2AA+=A#(AH)2；

充分性.假设(AH)2A#=A#(AH)2，则

(AH)2A#(En-AA+)=A#(AH)2(En-AA+)=O，

取共轭转置得

(En-AA+)(A#)HA2=O，

右乘A#A+得

(En-AA+)(A#)H=O，

再取共轭转置得

A#(En-AA+)=O，

即A#=A#AA+，所以A为EP矩阵，进而

(AH)2A=(AH)2A#A2=A#(AH)2A2=A(A#)2(AH)2A2=A(AH)2(A#)2A2
=A(AH)2A#A=A(AH)2AA#=A(AH)2AA+=A(AH)2，

故A为2-正规矩阵.

矩阵广义逆通常表现为某种矩阵与其相关逆矩阵之间满足相应的关系式，因此变化这些关系式中某个矩阵，则得到相应的矩阵方程，而矩阵方程在生产实践中的应用勿用多言.

由定理1可给出下面的矩阵方程AHXA#=A#AHX.

定理2设A∈n×n为群可逆矩阵，则

(i)A为正规矩阵当且仅当矩阵方程AHXA#=A#AHX在集合{A，A#，A+}中有解；

(ii)A为2-正规矩阵当且仅当矩阵方程AHXA#=A#AHX有解X=AH；

(iii)A为EP矩阵当且仅当矩阵方程AHXA#=A#AHX在集合{(A#)H，(A+)H}中有解.

证(i) 必要性.若A为正规矩阵，则A为EP矩阵，故A+=A#，因此

AHAA#=AHAA+=AH=A+AAH=A#AAH=A#AHA，

从而X=A为一个解；

充分性.① 若X=A为AHXA#=A#AHX的解，则AHAA#=A#AHA，注意到AA+A#=A#，所以

(En-AA+)AHAA#=O，

右乘AA+得

(En-AA+)AH=O，

从而AH=AA+AH，由推论3知A为EP矩阵，故AH=AHAA+=AHAA#=A#AHA，所以

AAH=AA#AHA=A#AAHA=A+AAHA=AHA，

故A为正规矩阵.

② 若X=A#为AHXA#=A#AHX的解，则AHA#A#=A#AHA#，右乘A2得

AHA#A=A#AHA，

由①知A为正规矩阵.

③ 若X=A+为AHXA#=A#AHX的解，则AHA+A#=A#AHA+，上式左乘(En-AA+)得

(En-AA+)AHA+A#=O，

右乘A2得

(En-AA+)AHA+A=O，

取共轭转置得

A+A2(En-AA+)=O，

左乘A#A得

A(En-AA+)=O，

从而A=A2A+，故A为EP矩阵，从而A+=A#，因此AHA#A#=A#AHA#，由②知A为正规矩阵.

(ii) 这是定理1的直接推论.

(iii) 必要性.若A为EP矩阵，则A#=A+，故

AH(A+)HA#=A+AA#=A#=A#A+A=A#AH(A+)H，

从而X=(A+)H为一个解；

充分性.① 若X=(A+)H为一个解，则

AH(A+)HA#=A#AH(A+)H，

即A+AA#=A#A+A=A#，所以A#A=(A+AA#)A=A+A，从而A为EP矩阵.

② 若X=(A#)H为一个解，则

AH(A#)HA#=A#AH(A#)H，

上式左乘(En-AA+)得

(En-AA+)AH(A#)HA#=O，

右乘A2A+得

(En-AA+)(A#A)H=O，

右乘AH得

(En-AA+)AH=O，

故AH=AA+AH，由推论3知A为EP矩阵.

定理3设A∈n×n为群可逆矩阵，则A为2-正规矩阵当且仅当矩阵方程AXAHA+=AHX在集合{A，AH}中至少有一个解.

证必要性.假设A为2-正规矩阵，则由引理1知，A为EP矩阵，故A+A=AA+，由于

A2AHA+=AHA2A+=AHAA+A=AHA，

故X=A为方程AXAHA+=AHX的一个解；

充分性.① 若X=A为方程的解，则A2AHA+=AHA，由于

AHA(En-AA+)=A2AHA+(En-AA+)=O，

所以AHA=AHA2A+，左乘(A+)H得A=A2A+，从而A为EP矩阵，故A+A=AA+，因此

AHA2=AHA2A+A=(AHA)A=A2AHA+A=A2AH，

故A为2-正规矩阵.

② 若X=AH为方程的解，则AAHAHA+=AHAH，上式左乘AA+得

AA+AHAH=AHAH，

右乘(A#)H得

AA+AH=AH，

两边取共轭转置得

A=A2A+，

故A为EP矩阵，从而

AHAHA=AAHAHA+A=AAHAHAA+=AAHAH，

再取共轭转置得

AHA2=A2AH，

故A为2-正规矩阵.

定理4设A∈n×n为群可逆矩阵，则A为2-正规矩阵当且仅当方程XA+AHA=AXAHA+在集合{A，A#，A+，(A#)H，(A+)H}中至少有一个解.

证必要性.A为群可逆矩阵且为2-正规矩阵，由引理1知，A为EP矩阵，则

AA+AHA=AHA=AHA2A+=A2AHA+，

所以A为XA+AHA=AXAHA+的一个解；

充分性.① 当X=A时，有AA+AHA=A2AHA+，右乘(E-AA+)得

AA+AHA(E-AA+)=A2AHA+(E-AA+)=O，

左乘(A+)H(A#)HAH得

(A+)H(A#)HAHAA+AHA(E-AA+)=O，

进而得到A(E-AA+)=O，即A=A2A+，所以A是EP矩阵，又AA+AHA=A2AHA+，得

AHA2=A2AH，

所以A是2-正规矩阵.

② 当X=A#时，有A#A+AHA=AA#AHA+，左乘A2得

AA+AHA=A2AHA+，

证明同①.

③ 当X=A+时，有A+A+AHA=AA+AHA+，左乘(E-A+A)得

(E-A+A)AA+AHA+=(E-A+A)A+A+AHA=O，

右乘A(A#)HA得

(E-A+A)AA+AHA+A(A#)HA=O，

进而有

(E-A+A)AA+AH(A#)HA=O，

即

(E-A+A)(A#AAA+)HA=O，

从而(E-A+A)A=O，故A=A+A2，所以A为EP矩阵，又由A+A+AHA=AA+AHA+，左乘A2，右乘A得

AHA2=A2AH，

所以A是2-正规矩阵.

④ 当X=(A+)H时，有(A+)HA+AHA=A(A+)HAHA+，右乘(E-AA+)得

(A+)HA+AHA(E-AA+)=A(A+)HAHA+(E-AA+)=O，

左乘(A+)H(A#)HAHAAH得

A(E-AA+)=O，

即A=A2A+，故A为EP矩阵，又

(A+)HA+AHA=A(A+)HAHA+，

左乘AAH易得

AHA=AAH，

故A为正规矩阵，所以也为2-正规矩阵.

⑤ 当X=(A#)H时，有(A#)HA+AHA=A(A#)HAHA+，右乘(E-A+A)得

A(A#)HAHA+(E-A+A)=(A#)HA+AHA(E-A+A)=O，

进而有AAH(A#)HA+(E-A+A)=O，左乘A+(A+)HAHA+得

A+A+(E-A+A)=O，

即

(A+)2=(A+)3A；

另一方面，因为

rank(A)=rank(AA#A)≤rank(A#A)≤rank(A)，

所以rank(A)=rank(A#A).

同理:rank(A)=rank(A+A)=rank(A+)，因为rank(A)=rank(A#A)，所以

rank(A2)=rank(A#A2)=rank(A)，

又

rank(A2)≤rank(A+A2A+)≤rank(AA+A2A+A)=rank(A2)，

从而

rank(A2)=rank(A+A2A+).

同理:rank((A+)2)=rank(A(A+)2A)，由于rank(A+A2A+)=rank(A(A+)2A)，所以

rank((A+)2)=rank(A2)=rank(A)=rank(A+)，

故A+为群可逆矩阵，又(A+)2=(A+)3A，故A+为EP矩阵，结合

(A#)HA+AHA=A(A#)HAHA+

得

(A+)HA+AHA=A(A+)HAHA+，

由④知A为2-正规矩阵.

3 结 论

本文介绍了一种新型的矩阵广义逆，即2-正规矩阵，这类矩阵是正规矩阵的真正推广，遗传了正规矩阵的一些性质.通过构造矩阵理论中流行的矩阵方程的解的存在性来研究2-正规矩阵，丰富了矩阵广义逆的研究内容与研究方法，同时这种研究手法可推广到半群，环上，C*-代数及算子代数的广义逆的研究中，因而具有理论上的意义.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.