基于DP的随机模型预测控制能量管理研究

马永娟 尹燕莉 马什鹏

（重庆交通大学机电与车辆工程学院）

近年来，有越来越多的学者应用模型预测控制（Model Predictive Control,MPC）来解决混合动力汽车能量管理优化问题[1-11]。它的主要原理是可以通过提前预测获取未来有限时间内的车辆运行信息，然后实施转矩的优化分配。可采用指数预测[12]、马尔科夫链[13]等方法预测未来时间内的车辆运行状态，然后优化算法[14-17]对预测信息进行求解。本文以超轻度混合动力汽车为研究对象，提出基于动态规划（DP）求解的随机模型预测控制能量管理策略。

1 超轻度混合动力汽车模型

1.1 系统结构与参数

本文对一款具有并联结构的超轻度混合动力汽车展开研究。其主要部件除了发动机、电动机及电池外，增加了一个回流式无级自动变速传动系统实现动力源之间的传递。该车具有纯发动机驱动、纯电机驱动、行车充电及制动能量回收4个工作模式。结构简图如图1所示。

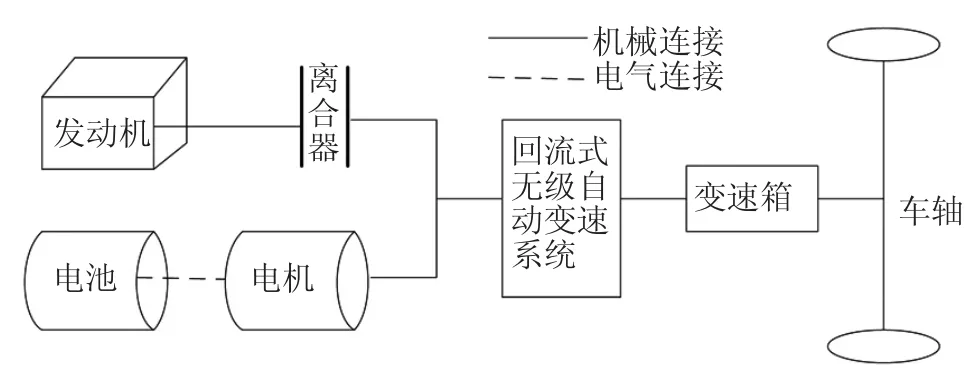
图1 超轻度混合动力汽车结构简图

1.2 车辆动力学模型

汽车在行驶的过程中，需要克服滚动阻力、空气阻力以及加速阻力（本文不考虑坡度阻力）。车辆在任意工况下的整车纵向动力学模型如式（1）：

式中：Tq——车辆需求转矩，N·m；

m——整车质量，kg;

g——重力加速度，m/s2；

f、Cd、δ——车辆的轮胎滚动阻力系数、空气阻力

系数、旋转质量换算系数；

A——迎风面积，m2；

d v/d t——车辆加速度，m/s2；

r——车轮半径，m。

2 基于DP的随机模型预测控制能量管理策略研究

2.1 基本理论介绍

2.1.1 模型预测控制原理

模型预测控制(MPC)是一种先进的控制方法，在工业控制中得到广泛应用。它主要以不同预测模型为基础，预测系统未来输出，采用滚动优化原则，在有限时域内反复在线优化得到最优的控制量。模型预测控制的框架结构如图2所示，可以分为3个部分：预测模型、滚动优化及反馈校正。其基本思想可以概括为：在每一个采样时刻，利用预测模型结合当前测量信息，采用优化算法在线滚动求解一个有限时域的优化问题，并将所得优化解的第1个元素作用于被控系统，将实际输出值反馈给预测模型修正预测值，并刷新优化问题重新求解[18]。，然后在下一采样时刻重复此过程直到有限时域结束。

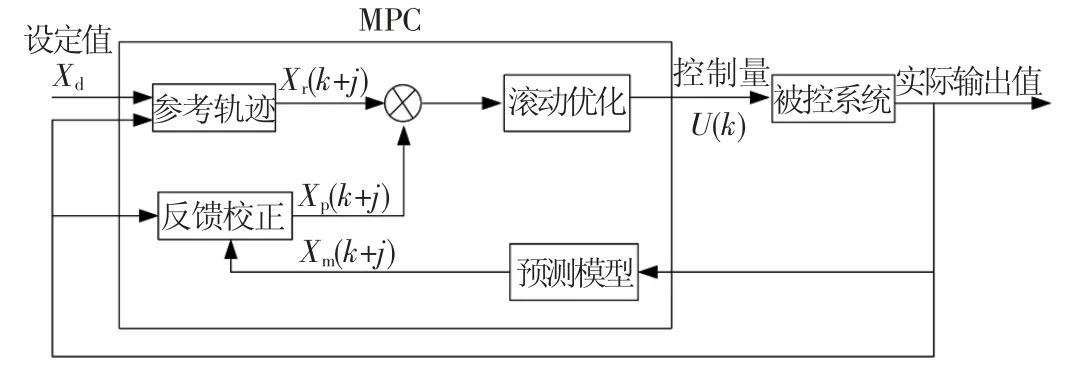
图2 模型预测控制总体框架图

2.1.2 动态规划原理

动态规划作为一种全局优化算法，本质是求解多阶段的决策问题。假设将待求解的问题看作是一个整体，把整体划分为有限个相互关联又具有独立性的个体，通过直接求解各个个体之间的决策问题，会得到多个决策序列，能够使整体的效果达到最优的决策序列就是动态规划算法所求出的问题的解。

动态规划的求解过程可概括为：逆向计算、正向寻优。逆向计算就是通过将待求问题分解为n个阶段，从最后1个阶段n开始，依次向前直至第1个阶段，迭代计算每个阶段每一状态下的最优目标函数值，从而得到与之相对应的最优控制变量。正向寻优就是基于逆向计算的结果，给定1个初始值，通过状态转移方程插值得到第1阶段至最后1个阶段的最优控制变量序列。动态规划原理如图3所示。

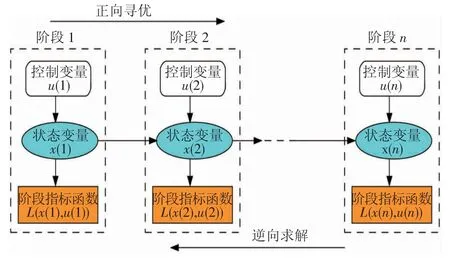
图3 动态规划原理图

2.2 基于DP的随机模型预测控制能量管理策略

利用模型预测控制对混合动力汽车进行能量管理，就是对未来一段时间内的电机转矩和发动机转矩进行最优分配。首先基于马尔可夫模型预测出有限时域内的加速度信息，然后采用DP算法进行优化求解，获得转矩分配序列。利用反馈机制实现闭环控制，获得最优的分配结果。

2.2.1 基于马尔可夫模型的加速度预测

预测模型相当于整个MPC能量管理策略框架中的“基石”，通过预测模型提前获知混合动力汽车未来一段时间内的运行状态，如车速、加速度及需求功率等信息，便可以根据当前时刻车辆的运行状态在预测时域内运用优化算法控制车辆性能达到该时域内的最优状态，从而获得更高的燃油经济性。

在车辆运行时，加速度的变化具有随机性，能够准确描述汽车的实际行驶过程，且未来某一时刻的加速度只取决于当前时刻的加速度，与历史加速度信息无关，具有马尔可夫性质，因此，可建立马尔可夫加速度预测模型对加速度进行预测。

构建马尔可夫加速度预测模型的关键是计算加速度的转移概率矩阵，转移概率矩阵的每一个元素代表汽车加速度从当前状态转移到下一状态的概率，如式（2）。选取概率最大的值作为加速度的实际值，从而确定下一时刻的加速度变化。

式中：a(k)、a(k+1)——当前时刻和下一时刻的加速度；

Pi,j——加速度由当前状态i转移到下一状态j的概率。

可根据式（3）来计算转移概率矩阵。

式中：Si——加速度由当前状态i转移的总次数；

Si,j——在预测时域p内，加速度由当前时刻状态i转移到下一状态j的次数。

选取ECE_EUDC、UDDS2种工况来提取加速度信息。将加速度（-1.5～1.5 m/s2）按一定间隔离散，采样步长取1 s，预测时域为p。根据以上所建立的马尔可夫加速度预测模型，对加速度进行预测。

图4表示车速为40 km/h时加速度的转移概率。由图中可以看出，加速度的转移概率基本呈对角线分布，分布较集中。这是因为在1 s的时间范围内，实际驾驶时通常不会改变行驶状态，所以加速度涵盖的变化信息较少，相差不大，使得下一时刻加速度与当前时刻加速度分布在相近区间。

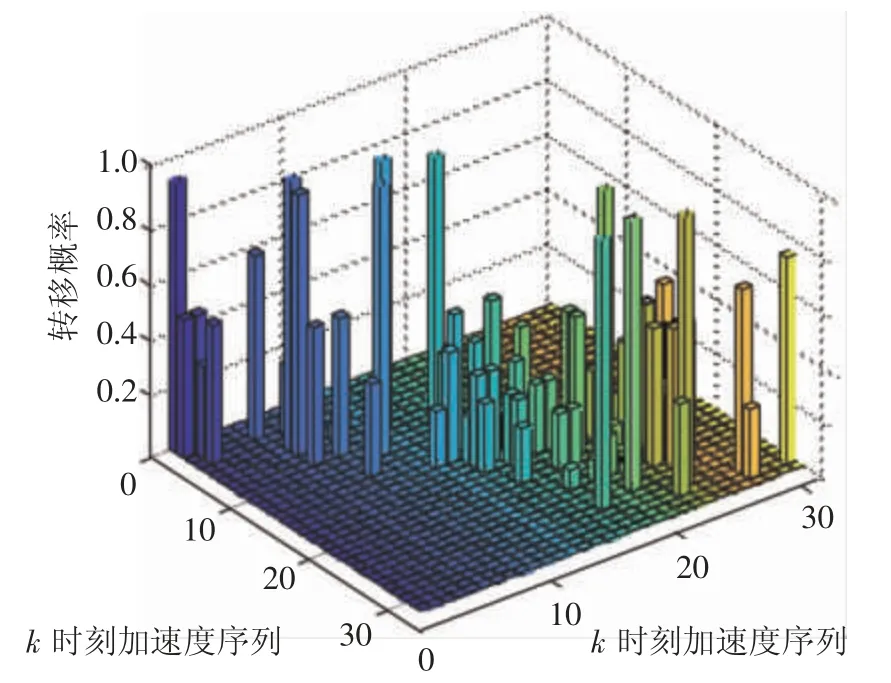
图4 v=35 km/h时加速度的转移概率

2.2.2 基于DP求解的滚动优化过程

根据马尔可夫模型预测获得的加速度信息，通过式（1）求解获得预测时域内的需求转矩。将燃油消耗作为优化目标，选取电机转矩Tm为控制变量，电池SOC为状态变量，采用DP求解有限时域内最优的转矩分配。

1）目标函数和约束条件

通过等效因子将电池能量变化等效为燃油消耗，构建以整车等效燃油消耗量最小以为目标的回报函数，如式（4）所示：

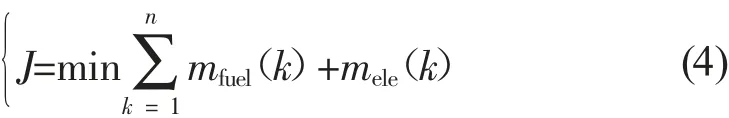
式中：mfuel（k）——当前k时刻发动机燃油消耗量，g；

mele（k）——当前k时刻电池等效燃油能量，g。

在优化过程中，每一阶段的决策之后，会引起状态的转移，状态转移方程如式（5）：

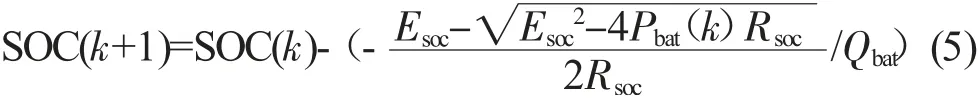
式中：SOC(k)、SOC(k+1)——表示当前k时刻和下一时刻的荷电状态；

Esoc——当前状态下的电动势；

Rsoc——表示当前状态下的内阻；

Qbat——电池容量；

Pbat（k）——当前k时刻的电池功率。

同时，为防止转矩、转速等因素对优化结果造成干扰，因此，在预测时域k～k+p对相关变量做如下约束：

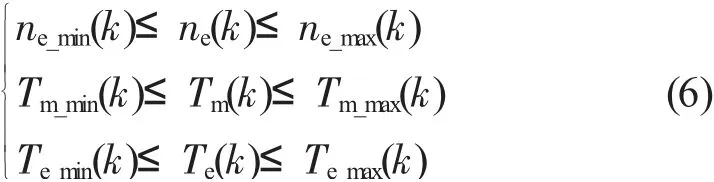
式中：ne(k)——k时刻的发动机转速，r/min；

ne_max(k)、ne_min(k)为k时刻发动机转速的最大、最小值，r/min；

Tm(k)——k时刻的电动机转矩，N·m；

Tm_max(k)、Tm_min(k)——k时刻电机转矩的最大、最小值，N·m；

Te(k)——k时刻的发动机转矩，N·m；

Te_max(k)、Te_min(k)——k时刻发动机的最大、最小值，N·m。

2）DP优化求解过程

动态规划（DP）作为一种全局最优算法，在模型预测控制当中，对预测时域内的预测信息进行滚动优化求解，可提高计算效率，具体优化步骤如下：

（1）根据马尔可夫模型预测获取的加速度信息，结合式（1）求出预测时域内的需求转矩[Tm(k)~Tm(k+p)]；

（2）在预测时域k～k+p内，可将优化问题划分成p+1个子阶段[k，k+1，…，k+p]，并将状态变量SOC在约束范围内进行离散化处理；

（3）根据上文的目标函数和约束条件，首先从最后一个阶段k+p逆行求解，求出该阶段到上一阶段k+p-1的最小油耗值，并记录获得最低油耗时的控制变量Tm，依次逆向计算直到第k阶段，则整个逆向求解过程结束；

（4）从初始阶段开始正向寻优，根据k阶段的状态变量SOC(k)，插值找到SOC(k)所对应的最小燃油消耗量fuel(k)和电动机转矩Tm(k)，根据状态转移方程（式5）获得下一时刻的状态量SOC(k+1)，重复（3），直到k+p时结束，就能获得k～k+p内的最优电机转矩分配序列[Tm(k)，Tm(k+1/k)，…，Tm(k+p/k)]。

2.2.3 实施反馈校正

通过DP求解获得最优电机转矩分配序列之后，只将最优序列的第1个控制量Tm(k)施加给车辆。在下一个时刻，首先检测车辆的实际车速和加速度值，并将其反馈给预测模型，重新预测系统输出并实施优化求解，重复执行上述过程直到预测时域结束，即可获得预测时域内的最优转矩分配。整个控制过程的流程图如图5所示。

图5 基于DP的随机模型预测控制流程图

3 仿真结果分析

为验证所提控制策略的性能，利用Matlab/Simulink仿真平台，基于ECE_EUDC、UDDS标准循环工况进行整车仿真分析。选取预测时域为3 s，采样时间间隔为1 s；将电池SOC限定0.3~0.8之间，以0.1为间隔进行离散，SOC初始值设为0.6；将预测时域内的需求转矩以5 N·m的间隔进行离散。仿真结果如图6所示。图6a为仿真工况数据图，图6b为发动机转矩随仿真工况的车速变化轨迹，可以看出，在汽车加速情况下，所需要的车轮处转矩较大，发动机多呈工作状态，输出较大转矩。图6c、6d为电机转矩及电池SOC变化轨迹，可看出，当电动机转矩为正时，电机作为电动机，使用电能，使电池SOC下降；当电动机转矩为负时，电机作为发电机，进行发电，使电池SOC上升。综合观察图6，当车速较低、频繁启动时多用电动机驱动，当车辆速度较高时，多用发动机，同时给电池充电。这与我们平时熟知的混合动力汽车理想转矩分配结果相同，说明所提出的控制策略具有一定的可行性。

图6 仿真结果图

4 结论

本文将MPC控制理论与DP算法有效结合，实现了超轻度混合动力汽车良好的转矩分配控制。基于ECE_EUDC、UDDS标准循环工况为样本数据构建马尔科夫模型对加速度进行预测，对预测时域内的信息采用DP算法进行滚动优化求解，然后实施反馈控制获得最优转矩分配。将所提控制策略基于Matlab/Simulink平台进行仿真分析，仿真结果表明，发动机和电动机基本工作在最优转矩区域内，证明该策略能取得良好的控制效果以及实现超轻度混合动力汽车最优的能量管理。