基于多智能体强化学习的多园区综合能源系统协同优化运行研究

杨 照，黄少伟，陈 颖,2

(1.清华大学电机工程与应用电子技术系，北京 100084；2.青海大学新能源光伏产业研究中心，青海 西宁 810016)

1 引言

综合能源系统能够提高能源利用效率，促进可再生能源消纳[1]。作为用能终端侧的多能耦合系统，多能园区将园区中多种能源进行转换、分配与有机协调，给终端用能侧带来了更大的灵活性[2]。相比于各个园区单独运行，多个园区间的协同运行构成了多园区综合能源系统。多园区综合能源系统内的能量互济可进一步释放分布式资源的潜力，提高各个园区运行方式的灵活性，降低各个园区运行成本[3]。因此研究多园区综合能源系统协同优化运行方法对于提高系统经济性，促进可再生能源消纳具有重要意义[4]。

目前对多园区综合能源系统协同优化运行方法的研究有集中优化和分布式优化两种方法[5]。集中优化方面，文献[6]提出了一种基于可再生能源配额制的多园区综合能源系统优化调度模型，并采用集中优化进行求解，有效地提高了系统可再生能源消纳能力，并保证了系统的经济性；集中优化需要一个集中决策者，大量信息的传递会对通信造成较大负担，同时详细信息的传递也不利于保护园区的隐私[7]。分布式优化方面，文献[3]提出了一个基于能源交易的能源共享策略，以协调区域综合能源系统中互联的多能微网，并采用交替方向乘子法算法(Alternating Direction Method of Multipliers,ADMM)实现了能量分配的分布式优化；文献[8]研究了同一能源配送网络下多能源枢纽的协同优化运行问题，采用基于ADMM的分布式优化算法进行求解，保护了各能源枢纽的隐私，保证了调度的相对独立性。在多园区综合能源系统中，各个园区往往分属不同的管理者，根据最小化自身运行成本的目标进行自主调度决策，因此系统呈现出多利益主体特性。然而上述研究均以全局最优为目标，没有对各个园区之间的能量传递进行结算，忽略了多园区综合能源系统中的多利益主体特性，同时也缺乏对新能源出力以及多能负荷的多重不确定性的考虑。

基于数据驱动的强化学习算法(Reinforcement Learning,RL)无需对不确定量进行精准预测，目前已有较多的研究将强化学习应用于电力系统和综合能源系统的决策控制中[9,10]，文献[9]介绍了基于RL的模型和解决方案在频率调节、电压控制、能源管理方面的关键应用；文献[10]介绍了RL的最新进展以及在电力系统中应用的前景和挑战；文献[11]将深度强化学习算法(Deep Deterministic Policy Gradient,DDPG)应用于综合能源服务商的定价和调度决策中；文献[12]提出了一种基于无模型深度强化学习的多能园区实时自治能量管理策略，并验证了该方法在降低用户用能成本的同时处理不确定性的优越性能；文献[13]将RL和传统优化方法相结合，提出了一种双层强化学习模型，以实现综合能源系统的实时经济调度。但上述研究多将强化学习应用于将综合能源系统建模为单一主体的场景中，目前尚缺乏对强化学习应用于综合能源系统多主体场景中的研究。

因此，本文针对含多重不确定性的多园区综合能源系统多利益主体协同优化运行问题进行研究，采用强化学习算法进行求解。本文首先针对多园区综合能源系统建立基于内部市场和内部能量交易的整体模型；然后建立单个园区数学模型和内部市场出清机制；接着建立面向多智能体系统的马尔可夫博弈模型来描述多智能体强化学习任务，并建立基于多智能体深度确定性策略梯度算法(Muli-Agent Deep Deterministic Policy Gradient,MADDPG)的求解架构和训练方法；最后通过仿真验证本文所提方法在确定性场景中和不确定性场景中的表现。

2 多园区综合能源系统建模

2.1 多园区综合能源系统结构

本文研究的多园区综合能源系统的整体结构如图1所示。园区之间可以通过能量母线进行能量的双向传递，并通过内部市场进行结算。基于内部市场，能量富余的园区可以将多余的能量卖给其他园区，而不是低价卖给外部能源网络；能量不足的园区可通过内部市场购买能量，从而避免以较高的价格向外部能源网络买入能量。因此相比于各个园区单独运行，基于内部市场的多园区协同运行可充分发挥园区的灵活性和能量互补特性，降低各个园区的运行成本。

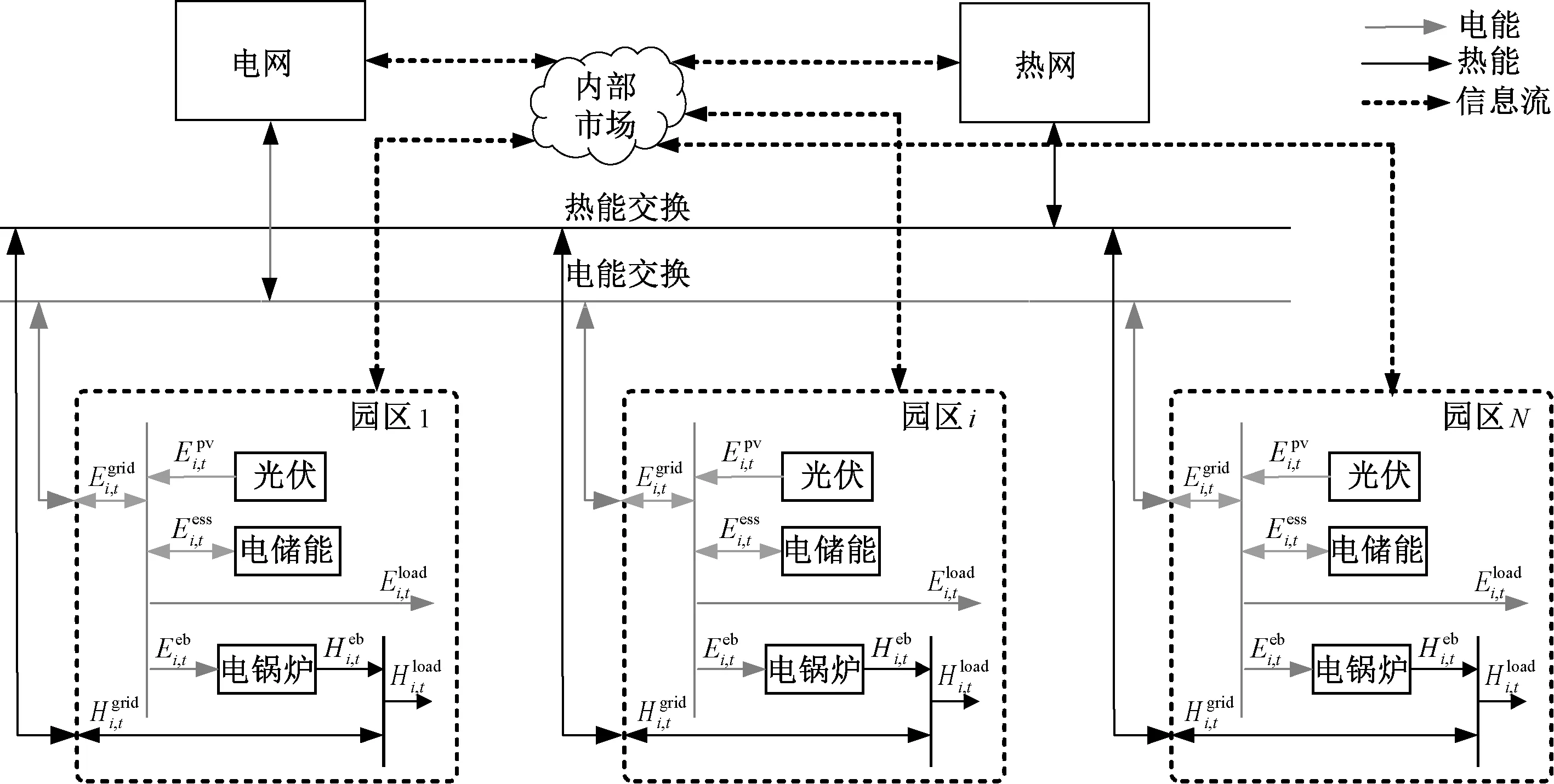
图1 多园区综合能源系统整体结构Fig.1 Structure of multi-park integrated energy system

在多园区综合能源系统中，各个园区优化自身调度策略，并将计划买入或售出的能量信息提交给内部市场，由市场管理者进行出清，多余或缺乏的能量再向外部能源网络卖出或买入。接下来介绍单个园区优化模型和内部市场出清机制。

2.2 单个园区模型

单个多能园区由新能源、储能、能量转换设备(如电锅炉、CHP等)和多能用户等构成。对于每个园区，园区管理者制定园区内部设备的运行计划从而实现园区的经济运行。园区管理者从外部能源网络或其他园区购入电、热等能源，经过能量存储和转换输出至内部多能用户，也可将多余的能量卖给其他园区或外部能源网络，其调度目标为最小化自身运行成本为：

minCi(xi)

(1)

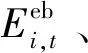
(2)

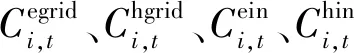
每个园区在运行时需要满足如下约束条件：

(1)能量平衡约束。

(3)

(4)

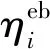
(2)储能动作约束。

(5)

(6)

(7)

SOCmin≤SOCt≤SOCmax

(8)

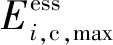
(9)

(4)传输线功率约束。

0≤Ei,t,b≤Ei,b,max

(10)

0≤Ei,t,s≤Ei,s,max

(11)

0≤Hi,t,b≤Hi,b,max

(12)

0≤Hi,t,s≤Hi,s,max

(13)

式中，Ei,b,max、Ei,s,max、Hi,b,max、Hi,s,max分别为电、热传输线路(管道)最大功率。

2.3 市场出清机制设计

本文采用内部市场实现园区间能量交易的结算，每个园区只需向内部市场提供自己的总售能量和购能量数据，无需提供详细的运行数据。

本文参考文献[14]微电网内部电力市场结算方案建立多园区内部电、热市场出清方法，电能市场价格出清如式(14)、式(15)所示，热能市场类似。

(14)

(15)

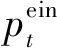
3 求解方法

本节首先将第2节中建立的多园区综合能源系统模型转换为马尔可夫博弈模型。在此基础上，本节建立了一种面向多园区综合能源系统的MADDPG算法，该算法采用“集中训练，分散执行”的方法求解此马尔可夫博弈问题。在虚拟环境中，智能体基于系统状态进行训练，在实际环境中，训练好的智能体可仅基于自己的局部观测给出最优动作，从而避免了通信负担过大和隐私泄露的问题，同时多智能体算法保证了多利益主体各自收益的最大化。

3.1 马尔可夫博弈模型

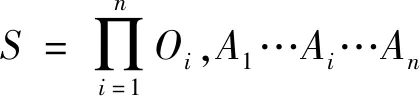
为简化问题，本文对各园区设计了相同的结构，同时对各个智能体设计了形式相似的观测空间、动作空间和奖励函数。

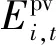
(16)

(17)

(18)

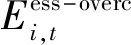
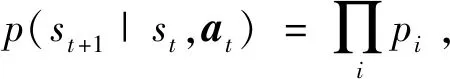
3.2 面向多园区综合能源系统的MADDPG算法

尽管已有较多研究应用深度强化学习算法求解电力系统和综合能源系统优化调度问题，但是对于多主体系统，直接使用多个强化学习智能体进行独立训练和决策往往达不到理想的效果。由于每个智能体的奖励依赖于所有智能体的动作，然而每个智能体的策略分布在训练过程中且都在不断变化，因此从单个智能体的角度看，其面对的环境是不稳定的。这种不稳定打破了强化学习算法所遵循的马尔可夫假设[15]，因此难以通过独立训练多个强化学习智能体得到稳定的策略分布。为了解决这个问题，本文采用具有“集中训练，分散执行”特点的MADDPG算法求解多园区综合能源系统协同优化问题。

MADDPG算法是DDPG算法[16]的多智能体版本，其模型结构如图2所示。每个智能体由需要全局信息的评论家网络(Critic)和只需要局部观测的动作家网络(Actor)组成[17]。MADDPG算法处理环境不稳定的关键是集中训练的评论家网络，在训练阶段，评论家网络输入系统状态，因此每个智能体都能捕捉到环境的动态变化，这使得MADDPG的训练过程更加稳定。MADDPG算法中，动作家网络和评论家网络均为多层全连接网络。由于评论家网络输入系统状态，因此其网络宽度大于只输入局部观测的动作家网络。本文建立的动作家和评论家网络的结构如图3所示。

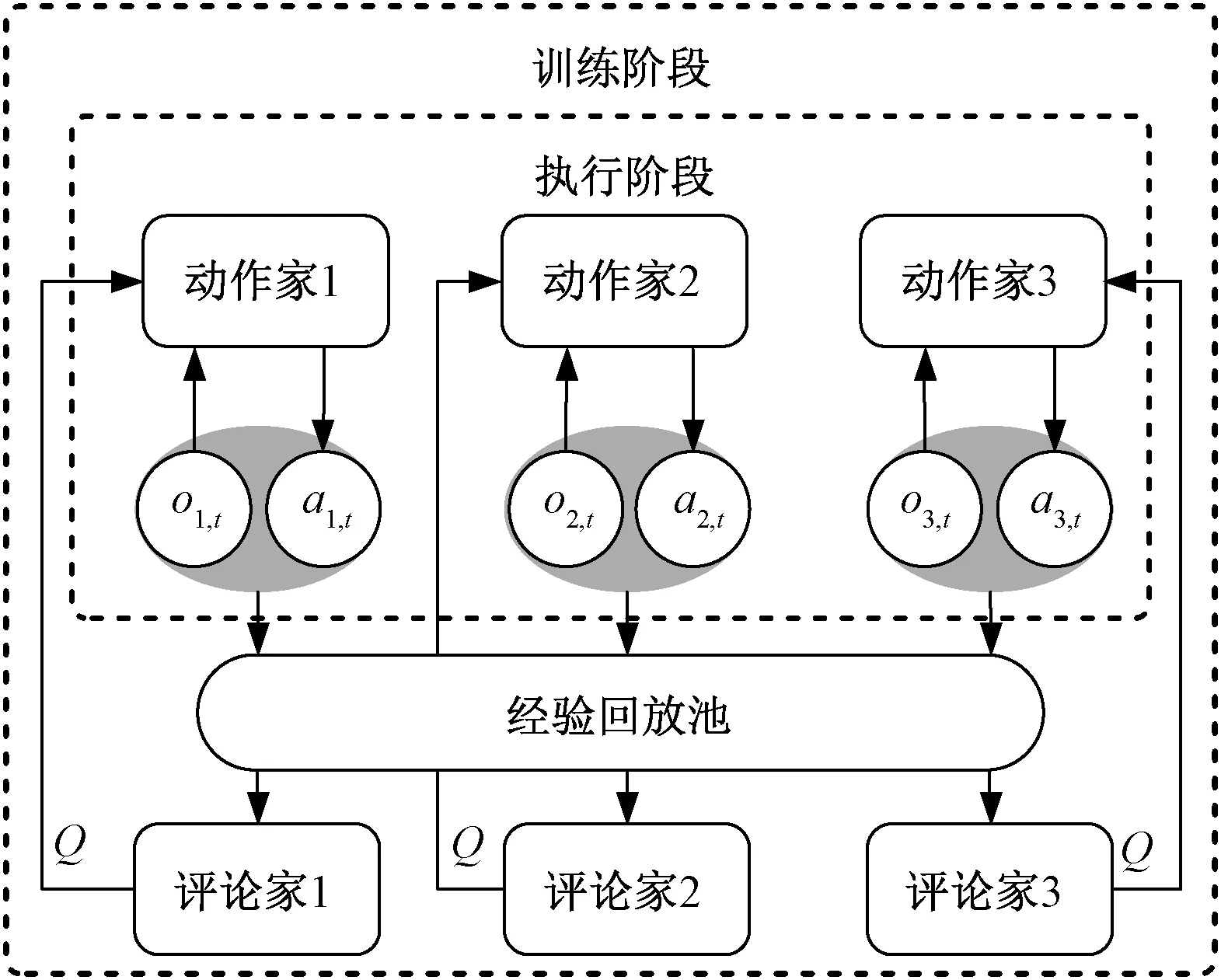
图2 MADDPG算法结构Fig.2 Structure of MADDPG algorithm

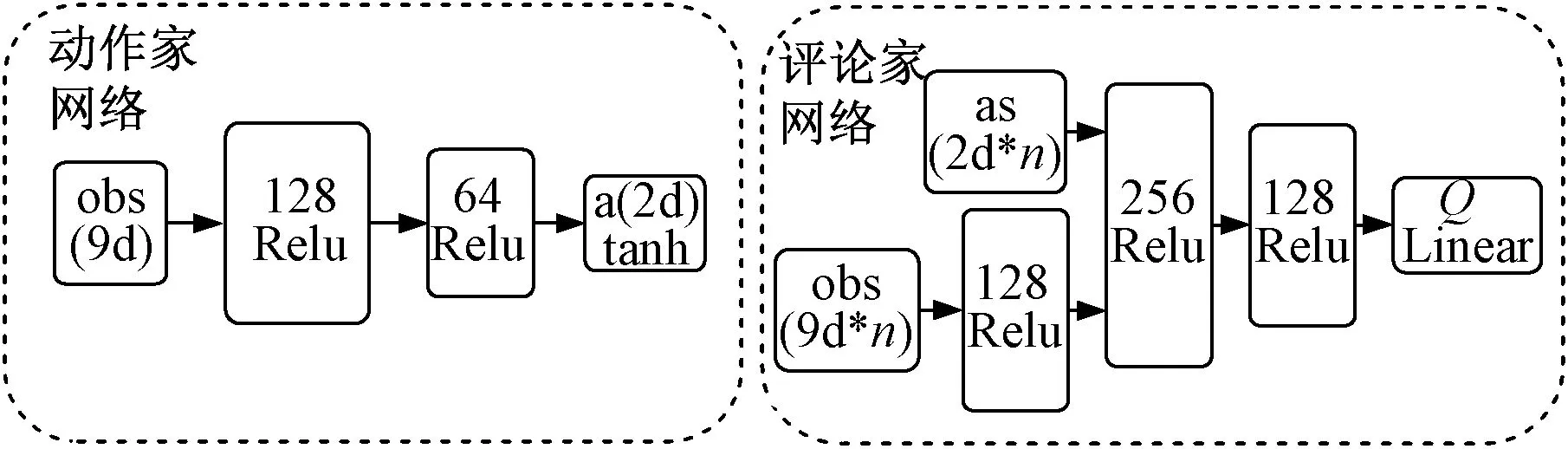
图3 动作家网络和评论家网络结构Fig.3 Structures of actor network and critic network

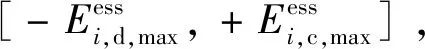
(19)

(20)

(1)评论家估计网络参数更新

评论家估计网络通过最小化损失函数LθQ来更新参数，损失函数的定义为：

(21)

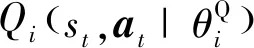
(22)

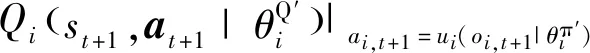
根据损失函数的梯度更新评论家估计网络的参数为：

(23)

式中，αQ为评论家估计网络的学习率。

(2)动作家估计网络参数更新

在训练过程中，动作家网络朝联合状态动作价值Q增大的方向更新参数以获得更大的价值，动作家网络参数更新的梯度为：

(24)

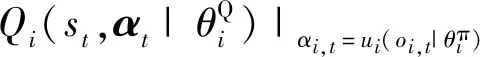
动作家估计网络的更新公式为：

(25)

式中，απ为动作家估计网络的学习率。

(3)目标网络参数更新

评论家和动作家目标网络参数由相应估计网络参数进行滞后更新，采用如式(26)、式(27)所示的软更新方式用以提高训练的稳定性和收敛性[18]。

θiπ′←τθiπ+(1-τ)θiπ′

(26)

θiQ′←τθiQ+(1-τ)θiQ′

(27)

式中，τ为软更新系数，且τ≪1。

在训练过程中，由于智能体与环境顺序交互产生的样本有关联，并不满足独立同分布的假设，因此不能直接用于训练。MADDPG算法采用同DDPG相同的经验回放机制，在与环境的交互中存储智能体与环境交互产生的经验序列e=(o1,t,oi,t,on,t,a1,t,ai,t,an,t,r1,t,ri,t,rn,t,o1,t+1,oi,t+1,on,t+1)，在样本池中随机抽样一个小批量样本用于训练，从而降低样本间的相关性。

3.3 基于MADDPG算法的多园区综合能源系统协同优化求解架构

在多园区综合能源系统的协同优化问题中，本文使用历史数据在虚拟空间进行离线训练，训练好的智能体在真实物理空间进行分散决策，既降低了执行阶段的通信负担，又保护了各个园区的隐私，多园区综合能源系统协同优化问题的求解架构如图4所示。

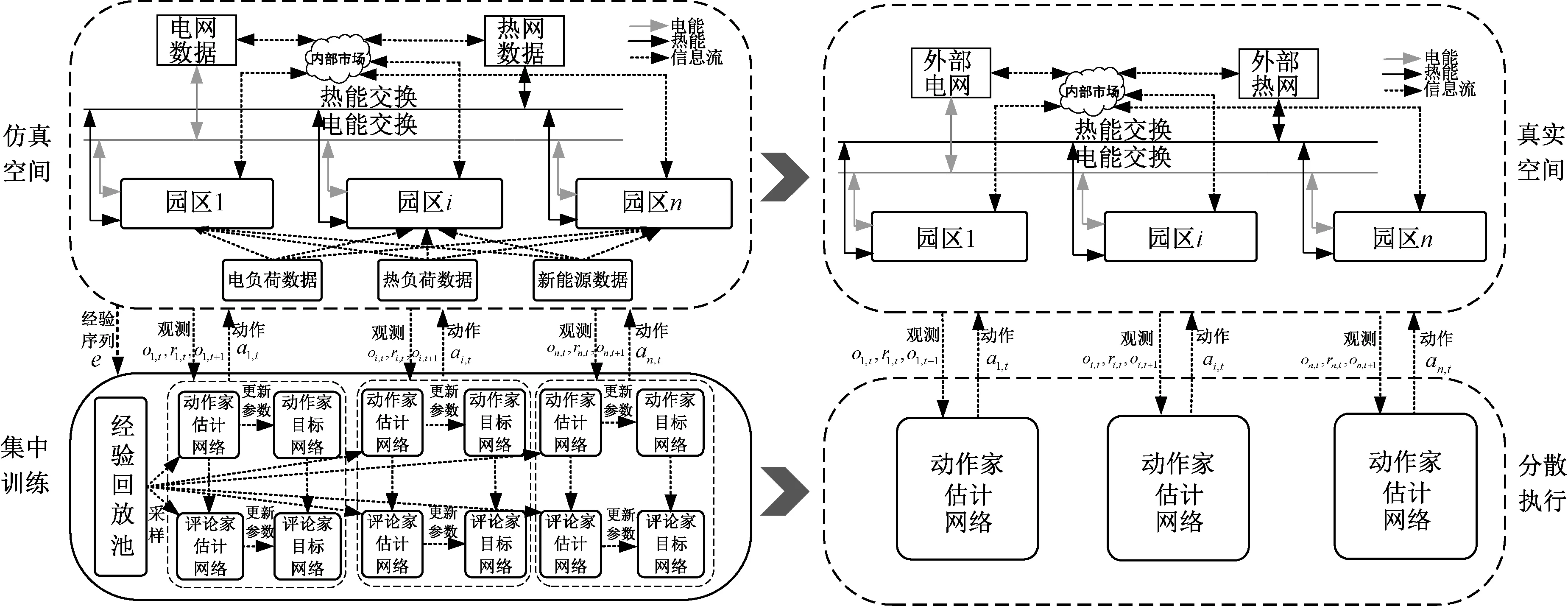
图4 多园区综合能源系统协同优化求解架构Fig.4 Solution framework for collaborative optimization of multi-park integrated energy system

其中MADDPG算法的训练过程如下：

(1)随机初始化每个智能体的估计网络参数(2)设置每个智能体的目标网络参数为相应的估计网络参数(3)forepisodek=1toMdo 1)每个智能体获得初始观测oi,0 2)fortimestep(hour)t=1toTdo ①通过动作家估计网络选择动作ai,t ②执行联合动作于环境,获得奖励(r1,t,…,ri,t,…,rn,t)和下一时段观测(o1,t+1,…,oi,t+1,…,on,t+1) ③将这一时步形成的经验序列e存储于经验池中 ④对每个智能体更新观测:oi,t←oi,t+1 ⑤foragenti=1tondo (a)采样小批量样本进行训练(b)根据式(23)、式(25)更新估计网络参数(c)根据式(26)、式(27)更新目标网络参数 ⑥endfor 3)endfor(4)endfor

4 算例分析

4.1 算例参数

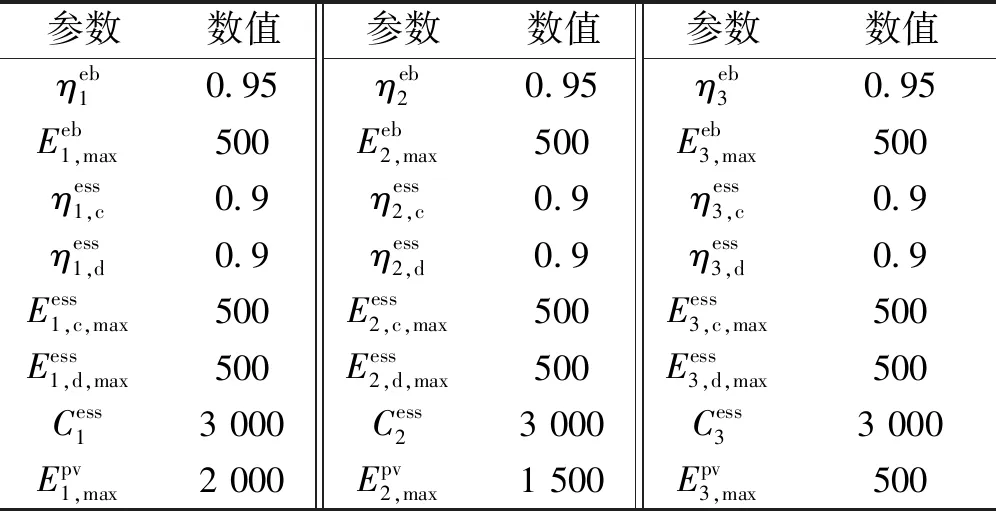
表1 设备参数Tab.1 Parameters of devices

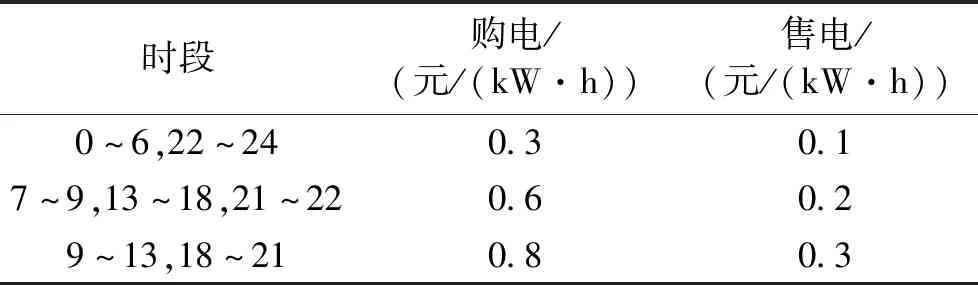
表2 电网电价Tab.2 Electricity price of power grid

本文设定各个园区智能体的网络结构相同，设置动作家网络的学习率为1e-4，评论家网络的学习率为1e-3，奖励衰减因子γ=1，表征决策目标为整个调度周期运行成本最小。

4.2 确定场景仿真结果分析

假设各园区的负荷和新能源出力可准确预测，基于预测值，可进行多园区协同优化，分别采取以下两种方案作为对比：①集中优化方法(Centralized Optimization，CO)，假设多园区综合能源系统有一个共同的管理者，根据各个园区的数据和参数进行集中统一调度，所得结果作为第一个参考；②单独优化方法(Individual Optimization，IO)，假设园区之间不能进行能量交换，各园区只能与外部网络进行能量交换，各园区单独优化的结果可作为第二个参考。理论上集中优化的结果是最优的，但也忽略了系统的多利益主体特性，而单独优化的结果运行成本最高。

一个典型的场景如图5所示，假设各个园区位置接近，各个园区新能源出力具有一定时空相关性，因此各个园区新能源出力曲线形状相似，但幅值不同。又由于各个园区用能曲线不同，因此各个园区有不同的能量特征，例如园区1新能源发电量较高，但是电热负荷水平比较低，园区3则相反。

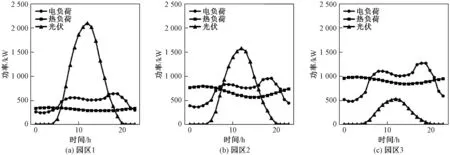
图5 典型场景下三个园区的新能源出力和电热负荷曲线Fig.5 Renewable energy outputs and multi energy loads curves of three parks in typical scenario

MADDPG算法得到的三个园区奖励总和的收敛曲线如图6所示。分析收敛曲线可得，随着训练回合的增加，各园区之间的动作逐渐协调，经过10 000次训练，三个园区奖励总和逼近集中调度的最优值。三种方法在典型场景下得到的运行成本见表3。由结果可得，进行集中优化时，多园区系统总运行成本为26 418.3元，园区2的运行成本为8 488.0元；而在本文所提方法下多园区系统总运行成本为26 796.5元，园区2用能成本为8 293.9元。由此可见，集中优化虽然使得整个多园区系统的总运行成本更低，但其因为集中决策调度的特性而损伤了园区2的利益，而本文所提的求解方法可以实现各个园区的独立自治，保护各个园区的利益。相比于各园区单独优化，本文所提算法下各个园区的用能成本均有下降，其中园区1和园区3的用能成本下降比例较大，且园区1开始盈利，这是由于园区1新能源出力较高，在内部市场扮演售能者(能量提供者)的角色。园区3新能源出力较低，在内部市场扮演购能者(能量接收者)的角色，基于MADDPG的多园区协同优化运行既提高了售能者的收益，也降低了购能者的成本。

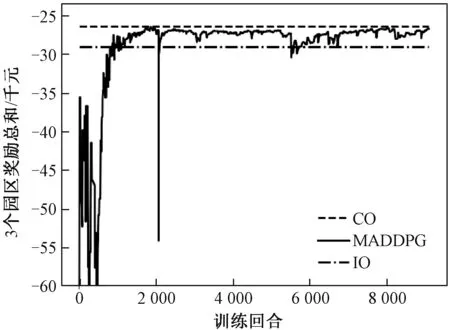
图6 园区智能体奖励总和的收敛曲线Fig.6 Convergence curve of total rewards of three parks

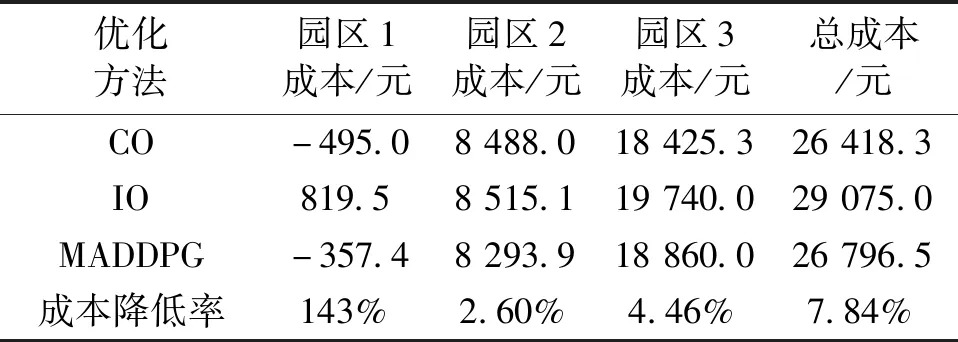
表3 典型场景下各园区运行成本统计Tab.3 Operation cost in typical scenario

内部市场的价格出清结果如图7所示，从出清曲线可得，内部热能市场全天处于供不应求的状态，内部电能市场在新能源高发时刻会出现短暂的供过于求状态，其余时刻也处于供不应求状态。

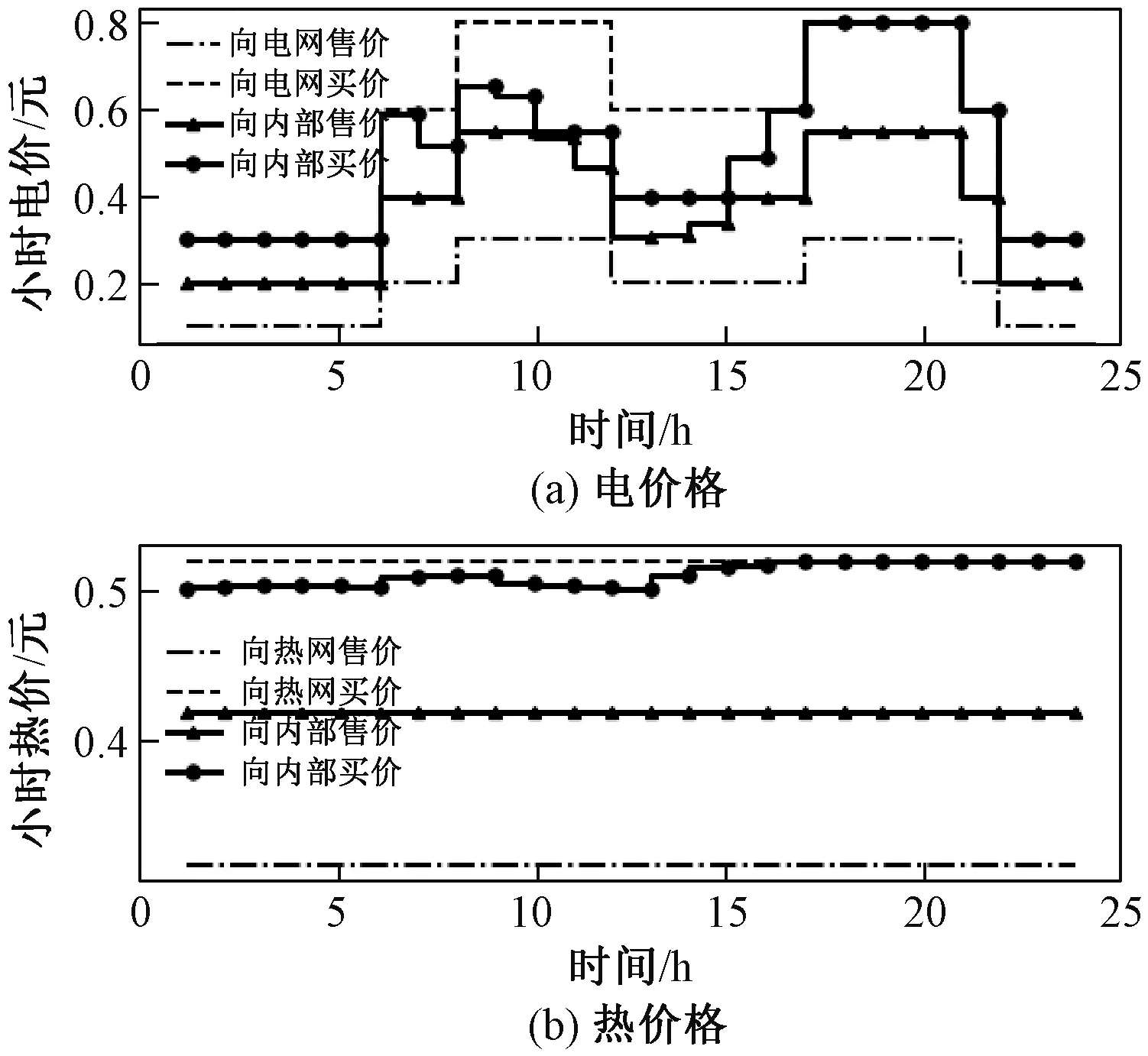
图7 典型场景下内部市场价格出清曲线Fig.7 Clearing price curve of the internal market

典型场景下各园区的能量交易量如图8所示，由于园区1新能源发电量较多，因此其向内部市场售电量较多，且其热负荷水平较低，因此园区1会在光伏高发时刻向其他园区出售多余的热能，而园区3由于新能源发电量最少，其在内部市场主要是一个购能者。

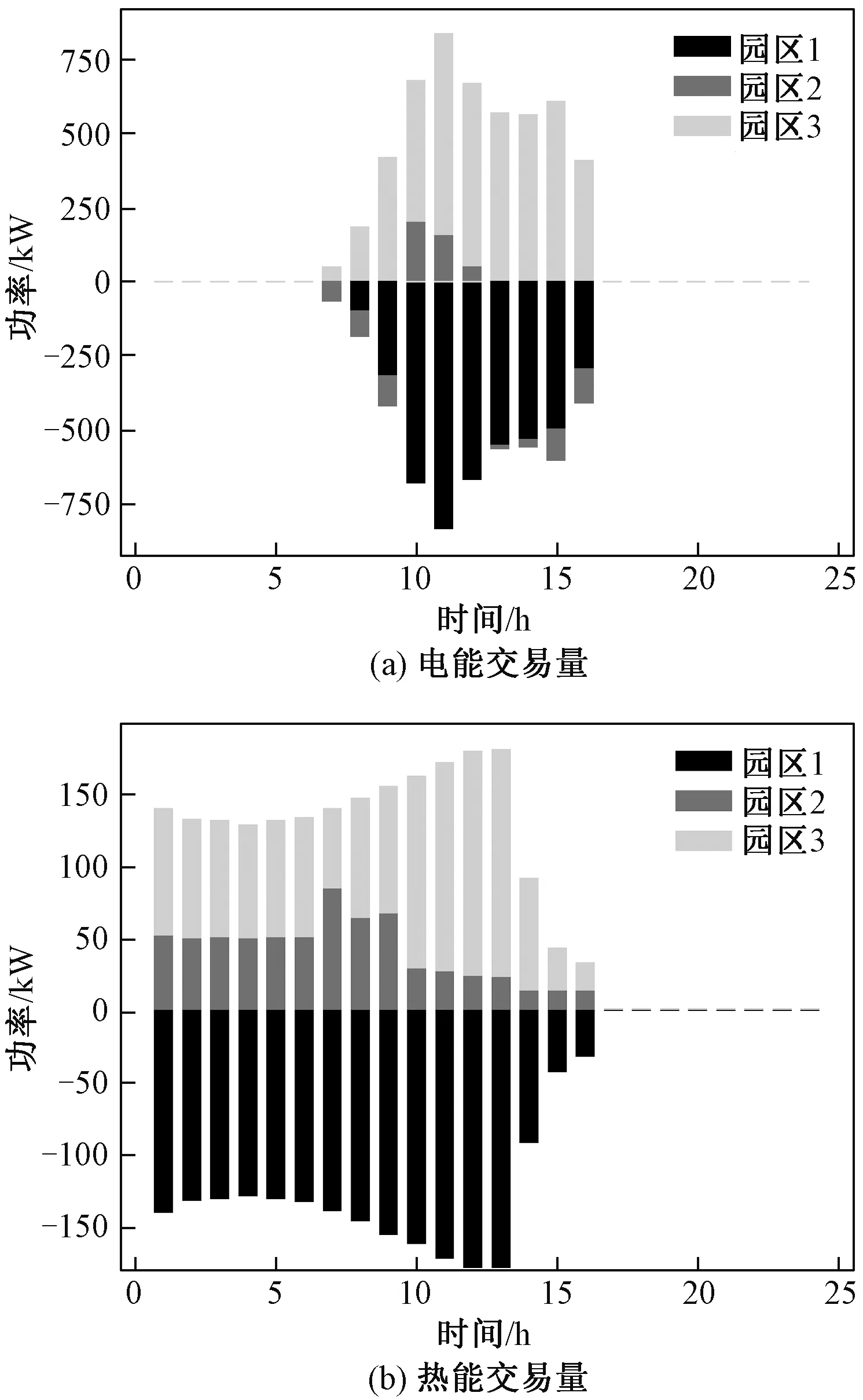
图8 典型场景下各园区能源交易量Fig.8 Energy trading of each park in typical scenario

4.3 不确定场景仿真结果分析

假设新能源出力、电热负荷等不确定变量不能准确预测，本文建立的求解方法是否能够实现多园区协同优化运行是本节研究的内容。为了刻画新能源出力和负荷的不确定性，本文基于采样的方式生成多种场景供模型训练，并生成100个随机测试场景测试模型的训练效果。假设新能源和负荷的基准曲线为4.2节建立的典型场景，并以基准曲线为均值、以0.1倍的基准值为标准差采样形成多种可能的场景。按照此方法生成园区1的100个测试场景如图9所示，园区2和园区3按照相同的方法进行场景生成。

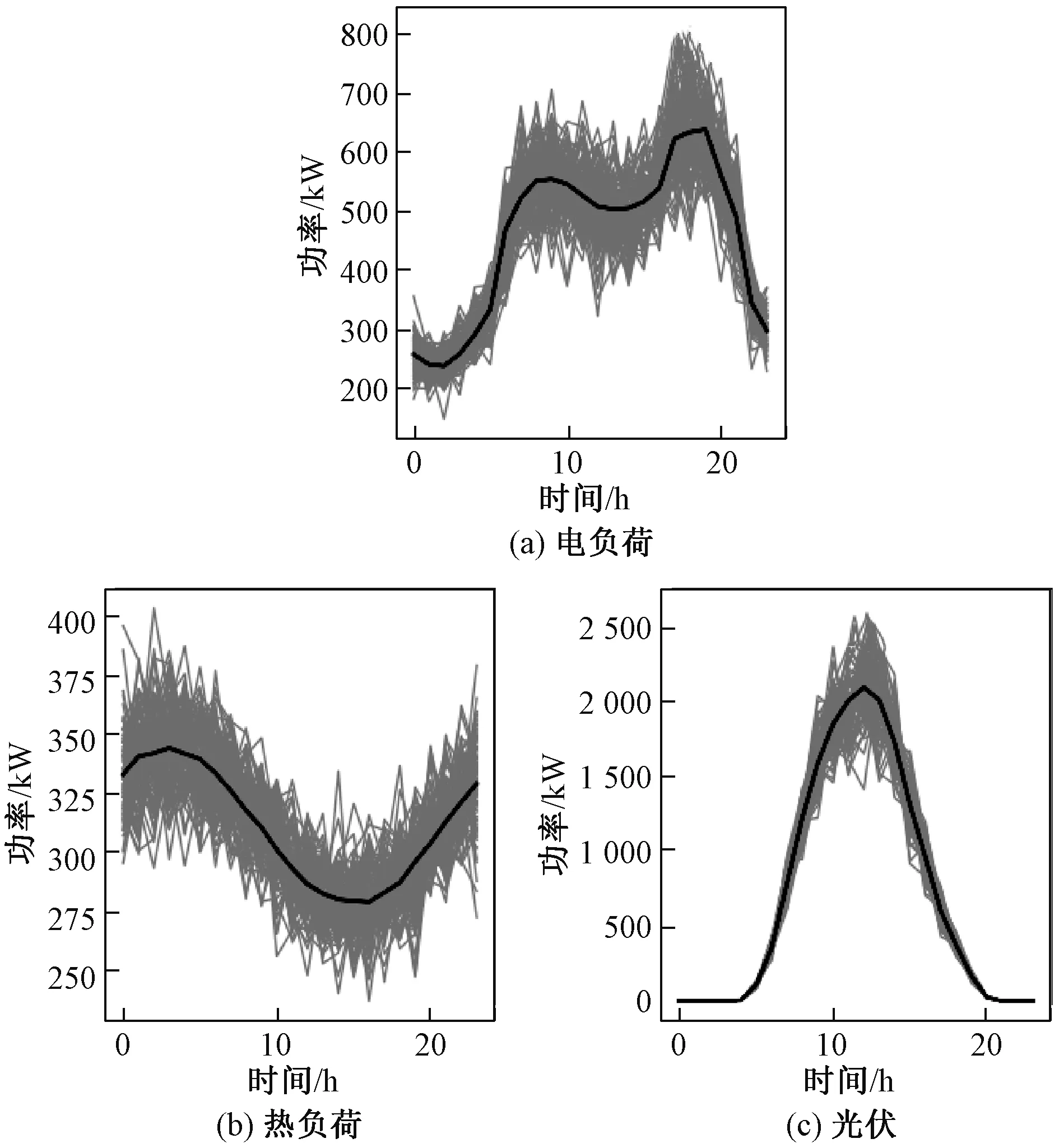
图9 园区1的100个测试场景Fig.9 100 test scenarios of the first park

在不确定性场景测试中，本文建立了两种对比算法：①基于新能源出力和负荷预测的集中优化(CO)；②无预测信息下园区独立运行的单时段最优算法(Short-Sight Individual Optimization，SSIO)，即当新能源出力和负荷预测值未知时，单独运行的园区只根据当前时段的实时信息做出单时段的最优调度，而不考虑整个调度周期最优。理论上三种优化方法得到的园区总运行成本关系为：基于新能源出力和负荷预测的集中优化<本文方法<园区独立运行的单时段最优算法。

系统智能体奖励总和的收敛曲线如图10所示，随着训练次数的增加，各园区的动作逐渐协调，智能体奖励总和逐渐收敛。100个测试场景的平均运行成本结果见表4，分析结果可得，在新能源出力和负荷信息未知的不确定性场景中，相比于各园区独立运行，基于MADDPG算法的多园区协同运行可降低各个园区的运行成本，系统总成本降低比例为15.44%。需说明的是，基于新能源出力和负荷预测的集中优化需要对多重不确定量进行准确预测，而基于MADDPG的协同优化在不需要预测值的情况下可接近集中优化的结果，同时本文所提方法保证了多利益主体通过内部市场进行合理的收益分配。

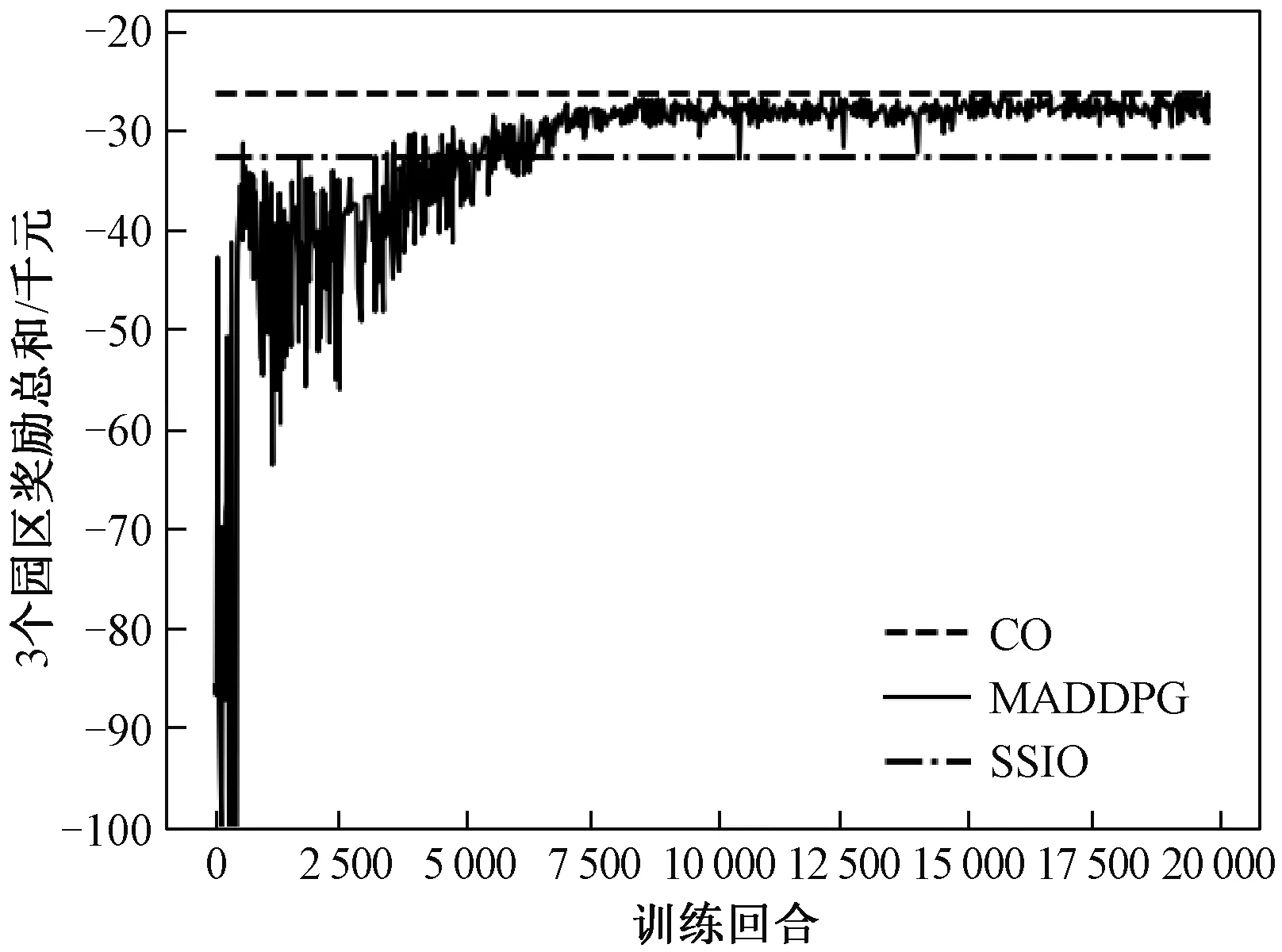
图10 不确定性场景下智能体奖励总和的收敛曲线Fig.10 Total rewards convergence curves in uncertain scenarios

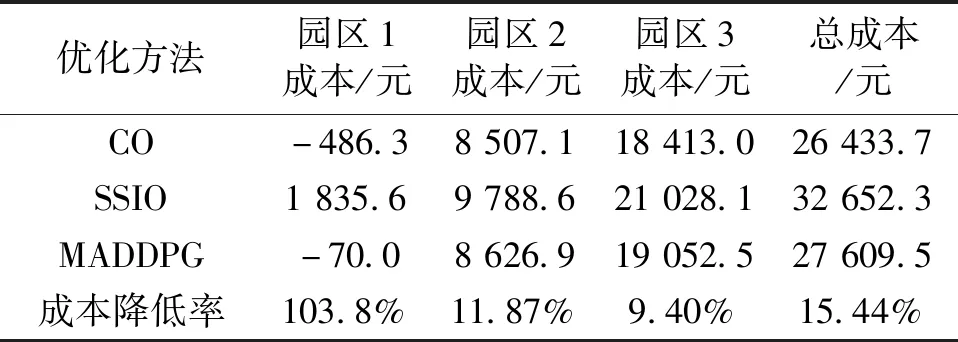
表4 100个测试场景下各园区平均运行成本统计Tab.4 Average operating cost under 100 test scenarios

5 结论

针对多园区综合能源系统协同优化运行中面临的缺乏多主体利益分配机制、隐私保护不足以及存在多重不确定量等问题，本文基于具有“集中训练、分散执行”特点的MADDPG算法建立了求解架构进行求解。确定性和不确定性场景下的仿真结果均表明，该算法可保证多利益主体合理的收益分配，在保护园区隐私的前提下降低各园区的运行成本，同时该算法不依赖于对多重不确定量的预测，可应用于实时调度中。

本文针对不确定量的建模还存在一定不足，后续研究计划则是研究如何基于真实历史数据训练模型；另外本文基于仿真空间进行离线训练，相比于离线训练，在线训练不需要建立镜像空间，但其常面临安全性低、效率低以及通信负担重等问题，因此后续工作将研究如何高效安全地实现在线训练。