新型RISE-LADRC逆变器电压控制策略

刘 勇，沈贵妃，章 兢,2，盘宏斌，马士翔

(1.湘潭大学自动化与电子信息学院，湖南 湘潭 411105；2.湖南大学电气与信息工程学院，湖南 长沙 410082)

1 引言

传统化石能源短缺和环境污染问题成为制约世界经济发展的两大阻碍[1]。具有污染少、可靠性高、能源利用效率高等优点的可再生能源和分布式发电成为应对能源、资源短缺的有效途径[2，3]。目前，微电网技术作为可再生能源和分布式发电的有效利用形式已成为研究的热点[4]。在微电网中，逆变器是连接分布式电源(Distributed Generation,DG)和各种负载的枢纽，其对系统的稳定起到关键作用。当离网逆变器中出现非线性负载和不平衡负载等强扰动时，传统自抗扰控制(Active Disturbance Rejection Control，ADRC)的抗扰性能还有待提升。因此，研究如何提高微网逆变系统的抗扰能力具有现实意义。

近年来，为了提高微网逆变器的抗扰性能，很多学者都提出了针对含扰动系统的控制方法，如自适应控制[5，6]、鲁棒控制[7，8]、滑模控制[9-11]等。自适应控制能通过自适应控制律来设计参数，可较好地处理参数不确定性，但扰动很大时的抗扰能力不足。鲁棒控制可以较好地解决未建模动态和扰动的问题，但鲁棒控制是高增益控制，可能受到高频噪声的影响。滑模控制能有效地抵抗未建模动态、参数摄动引起的干扰和不确定，实现系统在滑模面上的渐进稳定，但是传统滑模控制包含不连续控制会产生抖振。在处理扰动带来的不确定性时，这些方法因为特定的局限性不利于工程实用[12]。ADRC是韩京清先生针对比例-积分-微分(Proportion Integral Derivative,PID)控制器中存在的问题而提出的一种非线性控制策略，ADRC可以将系统中未建模动态、不确定动态和外部扰动全部视为总扰动，通过扩张状态观测器(Extended State Observer,ESO)对总扰动进行实时估计及补偿，从而消除扰动对系统的影响[13-15]。因此，ADRC不依赖于精确的数学模型，具有算法简单、鲁棒性强、动态性能好等优点[16]。而ADRC中非线性结构的理论分析困难，计算复杂度高，控制器需要调节的参数多[17]。将ESO和状态误差反馈律(State Error Feedback,SEF)这两个主要部分进行线性化处理，提出了线性自抗扰(Linear Active Disturbance Rejection Control，LADRC)，通过对观测器带宽和控制器带宽进行调节就能确定控制器的参数，方法简单，效果较好[18，19]。扩张状态观测器(Linear Extended State Observer,LESO)是LADRC的核心部分，其能实时估计系统中的总扰动，总扰动的反馈补偿环节也依赖于LESO，因此，LESO的观测能力直接决定了LADRC系统的控制精度。为了保证足够高的观测精度，需要尽可能地增大观测带宽[20]。但是，高观测带宽可能带来初始尖峰现象，估计尖峰会导致系统动态性能下降[21]。另外，文献[12]分析了增大观测器带宽可提高跟踪性能，但是也会放大高频噪声，导致系统控制量受噪声的影响产生大幅度的高频振颤。因此，在系统中出现强扰动时，不能只靠增大观测带宽来提高控制性能。为了增强抗扰能力，有很多学者提出了不同的改进方案。文献[22]和文献[23]通过设计时变增益观测器来保证观测误差收敛，并且有效抑制ESO高观测带宽带来的“初始微分峰值”现象，提高了观测精度。文献[24]设计改进二阶LADRC，在LESO中引入输出电压误差微分项，增加观测带宽以提高LESO的扰动观测能力，并在LESO中引入一阶惯性环节，增强高频噪声抑制能力，改进的LADRC具有较好的抗扰能力。上述文献都是从ESO层面来提高系统的抗扰能力，较少有文献对控制律进行研究。

综上，本文针对存在强扰动的离网逆变器系统，提出误差符号鲁棒积分(Robust Integral of the Sign of the Error，RISE)控制律和LADRC相结合的电压控制策略。首先，对离网逆变器建立数学模型，根据逆变器模型建立被控对象为输出电压的LADRC模型。然后，分析了当系统中出现强扰动时，有限的观测带宽不能准确地估计扰动，LADRC的控制精度会受其影响。其次，为了减小控制器对LESO的依赖，本文通过设计抗扰能力更强的RISE控制律来代替线性误差反馈律，RISE控制中的反馈增益能有效地抑制扰动对系统的影响[25，26]，提高系统的控制性能，并利用Lyapunov理论证明了所提控制策略的稳定性。最后，仿真和实验结果表明，相比传统LADRC控制，本文所提的RISE-LADRC控制对输出电压的跟踪精度更高，增强了逆变器系统的抗扰能力。

2 微网逆变器建模及LADRC控制器设计

2.1 微网逆变器建模

离网逆变器系统的结构如图1所示，本文中逆变器采用LC型滤波器进行滤波，DG是分布式电源；Lf、Cf、rf分别为滤波电感、滤波电容和滤波电感寄生电阻；uabc是逆变器桥臂侧三相输出电压；uoabc是逆变器三相输出电压；iLabc是滤波电感三相输出电流；iCabc是滤波电容三相输出电流；ioabc是逆变器三相输出电流；uodq是逆变器输出三相电压在dq轴的分量；vodq分别是三相参考电压在dq轴的分量。

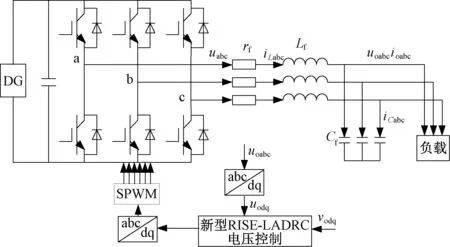
图1 离网逆变器控制框图Fig.1 Block diagram of off-grid inverter control

根据图1的离网逆变器结构，建立LC型离网逆变器在dq坐标系下的数学模型。

dq坐标系下逆变器的数学模型为：

(1)

(2)

式中，ud、uq分别为逆变器桥臂侧电压在d、q轴分量；uod、uoq分别为逆变器输出电压在d、q轴分量；iLd、iLq分别为滤波电感电流在d、q轴分量；iod、ioq分别为输出电流在d、q轴分量；ω为电网电压的角频率。

2.2 基于LADRC的电压控制

对式(2)求导后将式(1)代入得二阶微分方程：

(3)

根据式(3)中逆变器系统的输出电压uod和uoq来设计LADRC控制器，由于d、q轴方程具有对偶关系，下文中只对d轴进行分析，q轴的分析类似[27]。

由式(3)可知，离网逆变器系统的LADRC被控对象模型表示如下:

(4)

式中，uod为被控目标；b0为控制增益，b0=KPWM/LfCf；KPWM为逆变器增益；u为电压控制信号d轴分量；f为系统总扰动。

(5)

将式(4)中的f作为扩张状态变量，根据式(4)建立扩张系统的状态空间表达式：

(6)

式中，x1、x2、x3为系统的状态变量；y为系统输出；x1=uod为逆变器输出电压；x2为逆变器输出电压的微分；x3=f为系统总扰动；h为总扰动f的微分。

建立LESO扩张状态观测器：

(7)

可以求出式(7)的特征方程：

λ(s)=s3+β1s2+β2s+β3

(8)

根据文献[19]，当特征方程为理想状态时，λ(s)=(s+ωo)3。

β1=3ωo,β2=3ωo2,β3=ωo3

(9)

取前馈控制为：

(10)

将式(10)代入式(6)，可得

(11)

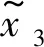
LSEF设计如下：

u0=kp(vod-z1)-kdz2

(12)

式中，kp和kd为控制增益，都是正数。

传统LADRC控制器由跟踪微分器(Tracking Differentiator,TD)、LESO、LSEF组成。本文中不使用TD，最终可以得到，传统LADRC控制器的整体结构如图2所示。

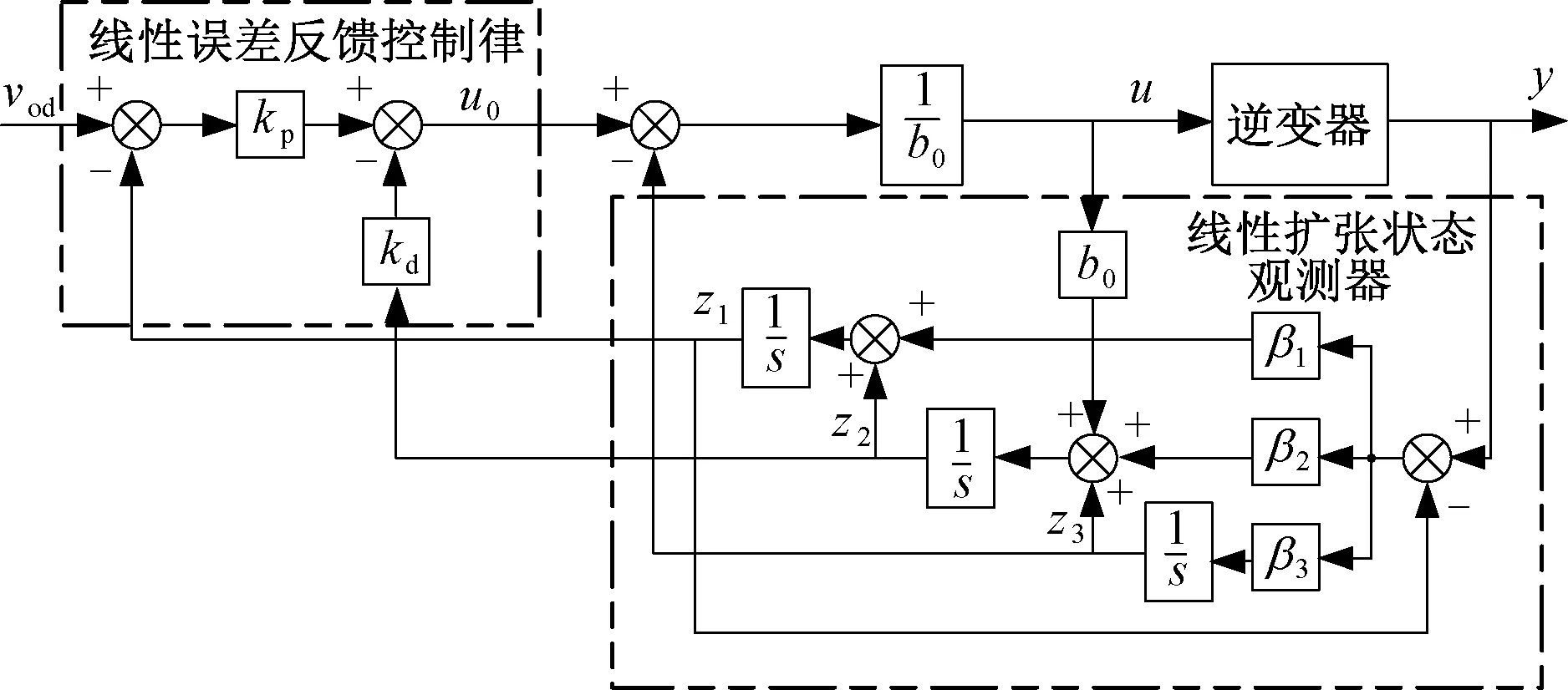
图2 传统LADRC整体控制图Fig.2 Block diagram of traditional LADRC control

3 设计RISE-LADRC控制器

3.1 设计RISE控制律

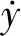
(13)

定义RISE控制律的误差变量为：

(14)

式中，α1和α2是RISE控制的控制增益。

将式(13)代入式(14)中得：

(15)

结合式(13)～式(15)得：

(16)

结合式(14)对式(16)做变换，可得：

(17)

将式(11)、式(15)代入式(17)中：

(18)

对式(18)求导，结合式(14)和式(15)，可得

(19)

(20)

假设扰动Nd存在如下关系：

‖Nd‖≤ξ1

(21)

(22)

式中，‖·‖为2范数。

引理1[28]：定义辅助变量L(t)为

L(t)=r(Nd-βsgn(e2))

(23)

如果符号函数增益β满足以下条件：

(24)

定义的辅助函数P(t)为：

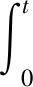
(25)

则有P(t)恒大于0。

辅助函数P(t)的导数为：

(26)

定义李雅普诺夫函数为：

(27)

对式(27)求导，结合式(14)、式(15)和式(26)得出：

(28)

令

(29)

对式(29)进行积分，结合式(14)，则可以得到RISE控制律为：

(30)

式中，α1、α2、ks为控制增益；β为符号函数增益。

3.2 设计RISE-LADRC控制器

本文中的RISE-LADRC控制器由LESO和RISE控制律组成。根据式(7)、式(10)、式(14)和式(30)可以得到RISE-LADRC控制器的结构如图3所示。

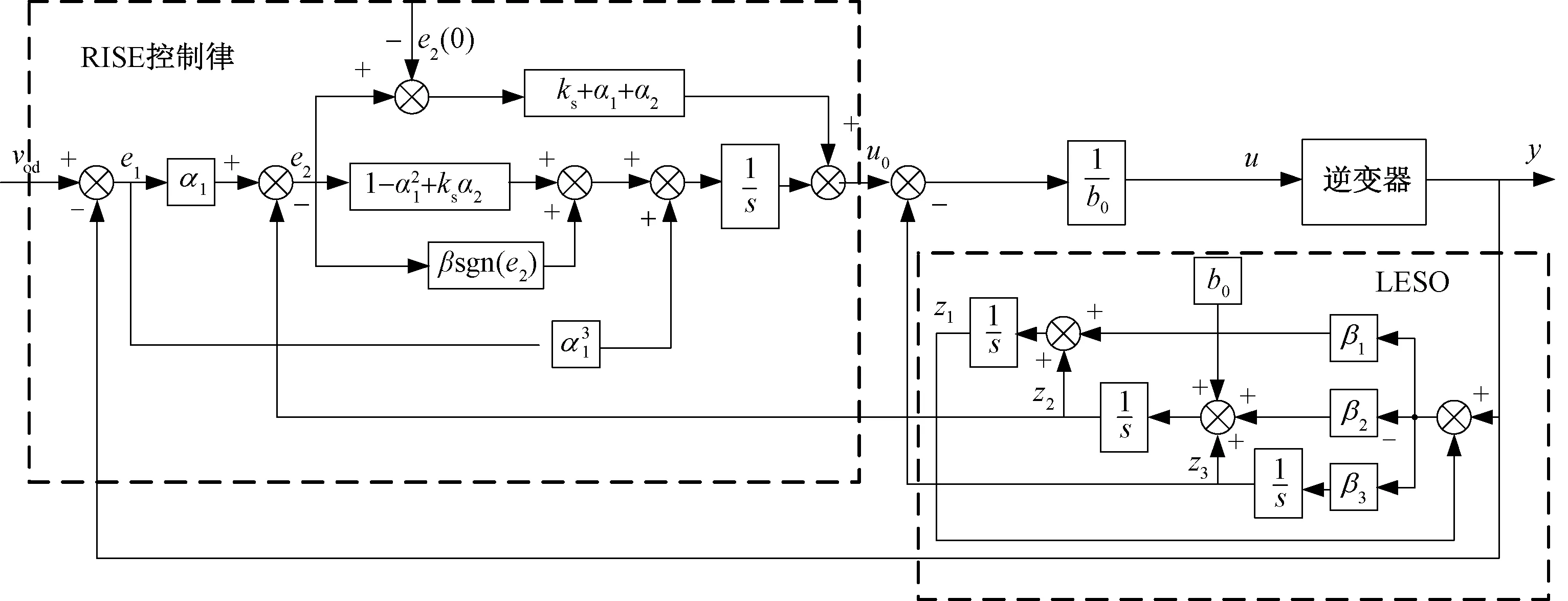
图3 RISE-LADRC控制结构图Fig.3 RISE-LADRC control structure diagram

4 稳定性分析

定理1给定一个系统如式(11)所示，若在满足式(24)的前提下，通过调节控制增益α1、α2和ks使其满足如下关系：

(31)

则式(30)中提出的RISE控制律能够保证e1、e2和r有界。

证明：根据稳定性分析，选取李雅普诺夫函数如式(27)所示。

将式(29)代入式(28)可得出：

(32)

文献[29]中证明被控对象的动态模型未知且扰动有界时，ESO的估计误差是有界的，即存在：

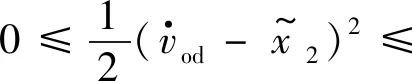
(33)

ϖ为一个有限正数。

z=[e1e2r]T

(34)

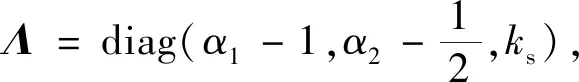
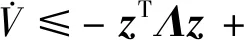
(35)

根据式(31)、式(34)和式(35)，定义如下紧集：

(36)

实现e1、e2和r有界的前提是控制增益α1、α2和ks满足式(31)，且根据式(36)可知，控制增益α1、α2和ks的取值越大则收敛速度越快，故控制增益α1、α2和ks的值可适当取大一点。

5 仿真及实验验证

5.1 仿真验证

为了验证本文提出的RISE-LADRC电压控制策略的可行性和有效性，基于Matlab/Simulink仿真平台，搭建三相离网逆变器系统仿真模型。表1～表3分别为逆变器仿真参数、二阶RISE-LADRC控制器参数、二阶传统LADRC控制器参数。

表1 逆变器仿真参数Tab.1 Inverter simulation parameters

表2 二阶RISE-LADRC控制器参数Tab.2 Second-order RISE-LADRC controller parameters

当离网逆变器系统出现不平衡负载和非线性负载工况时，分别采用RISE-LADRC、传统LADRC两种不同控制策略对上述工况进行仿真对比分析。

表3 二阶传统LADRC控制器参数Tab.3 Second-order traditional LADRC controller parameters

工况1：不平衡负载

0～0.1 s系统仅接入P=10 kW、Q=200 Var的公共负载，在0.1s时在负载端a相和c相间接入一个电阻Rb模拟不平衡负载。

图4(a)、图4(b)分别为两种不同控制策略下的三相输出电压波形图，0.1 s前负载端只接有公共负载，RISE-LADRC和传统LADRC中三相电压波形都比较平滑；0.1 s接入Rb=30 Ω的不平衡负载后，图4(a)中RISE-LADRC的三相输出电压波形发生微小抖动，迅速恢复到较好的平衡状态；图4(b)中传统LADRC的三相输出电压波形出现明显的不平衡现象。图4(c)和图4(d)分别为0.1 s时接入20 Ω、30 Ω、40 Ω、50 Ω的不平衡负载情况下的输出电压不平衡度对比图；图4(c)和图4(d)分别为两种不同控制策略下，不同阻值的负载对应的输出电压的不平衡度图，由图4(c)可知，RISE-LADRC输出电压的不平衡度受不平衡负载的影响较小，达到稳态时输出电压不平衡度皆低于0.5 %；由图4(d)可知，传统LADRC控制时，接入的不平衡负载阻值越小，对输出电压不平衡度的影响越大，达到稳态时输出电压不平衡度都高于0.5 %，最高达到1.9 %。综上分析，RISE-LADRC控制能更有效地抑制不平衡负载带来的电压不平衡现象。

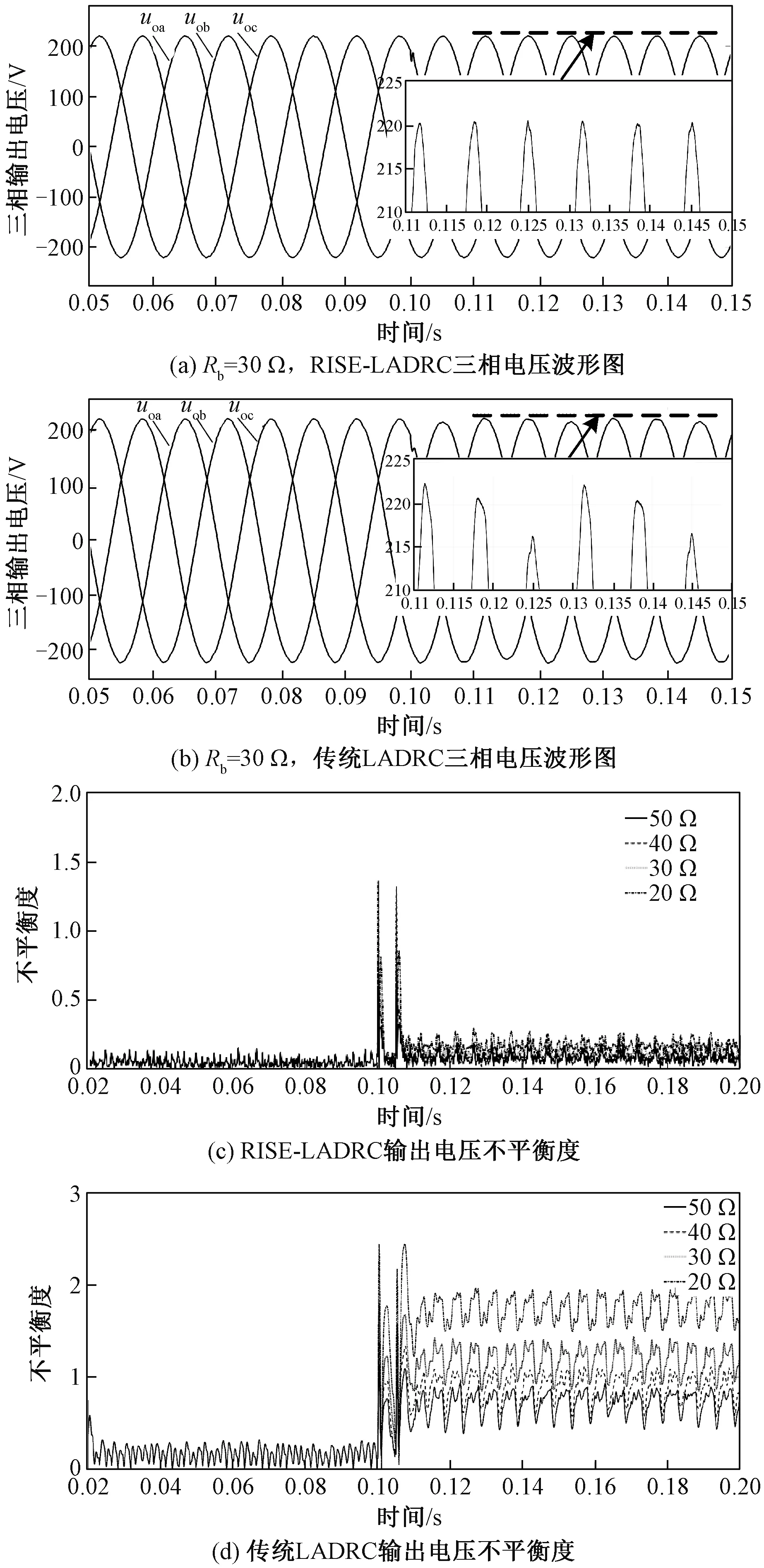
图4 接入不平衡负载结果对比Fig.4 Comparison of results with two-phase unbalanced load

不平衡负载Rb=30 Ω的情况下，图5(a)为两种不同控制策略下d轴输出电压响应时间图，其中，RISE-LADRC输出电压的响应时间为0.002 8 s，而传统LADRC输出电压的响应时间为0.014 s；图5(b)为两种不同控制策略下d轴输出电压的跟踪误差对比图，RISE-LADRC输出电压标幺值的波动范围为0.996～1.005 pu；传统LADRC输出电压标幺值的波动范围为0.979～1.022 pu。综上可知，RISE-LADRC的快速性更好、跟踪误差更小、跟踪精度更高。

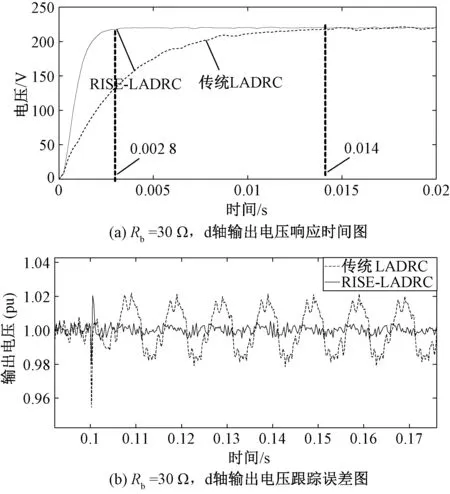
图5 不平衡负载条件下的动态性能图Fig.5 Dynamic performance graph under non-linear load conditions

工况2：非线性整流负载

0～0.1 s系统仅接入P=10 kW、Q=200 Var的公共负载，在0.1 s时在负载端接入一个整流负载Rf模拟三相非线性负载。

图6(a)、图6(b)分别为两种不同控制策略下三相输出电压波形图，0.1 s前负载端只接有公共负载，RISE-LADRC和传统LADRC中三相电压波形都比较平滑，波形畸变较小；0.1 s接入Rf=30 Ω的非线性负载后，两种控制策略都能使系统保持稳定运行。但是，由图6(c)和图6(d)可知，RISE-LADRC的三相输出电压总谐波失真(Total Harmonic Distortion，THD)为2.58 %，传统LADRC的三相输出电压THD为4.52 %，传统LADRC的三相输出电压波形发生更加严重的畸变。图6(e)为0.1s时分别接入25 Ω、30 Ω、35 Ω、40 Ω、45 Ω、50 Ω、55 Ω、60 Ω的非线性负载，不同阻值对应RISE-LADRC的三相输出电压THD分别为2.96 %、2.58 %、2.28 %、2.08 %、1.88 %、1.73 %、1.59 %、1.51 %，不同阻值对应传统LADRC的三相输出电压THD分别为5.17 %、4.52 %、3.99 %、3.57 %、3.28 %、3.04 %、2.79 %、2.61 %。综上分析，在接入不同阻值的非线性负载情况下，RISE-LADRC对谐波的抑制能力强于传统LADRC。

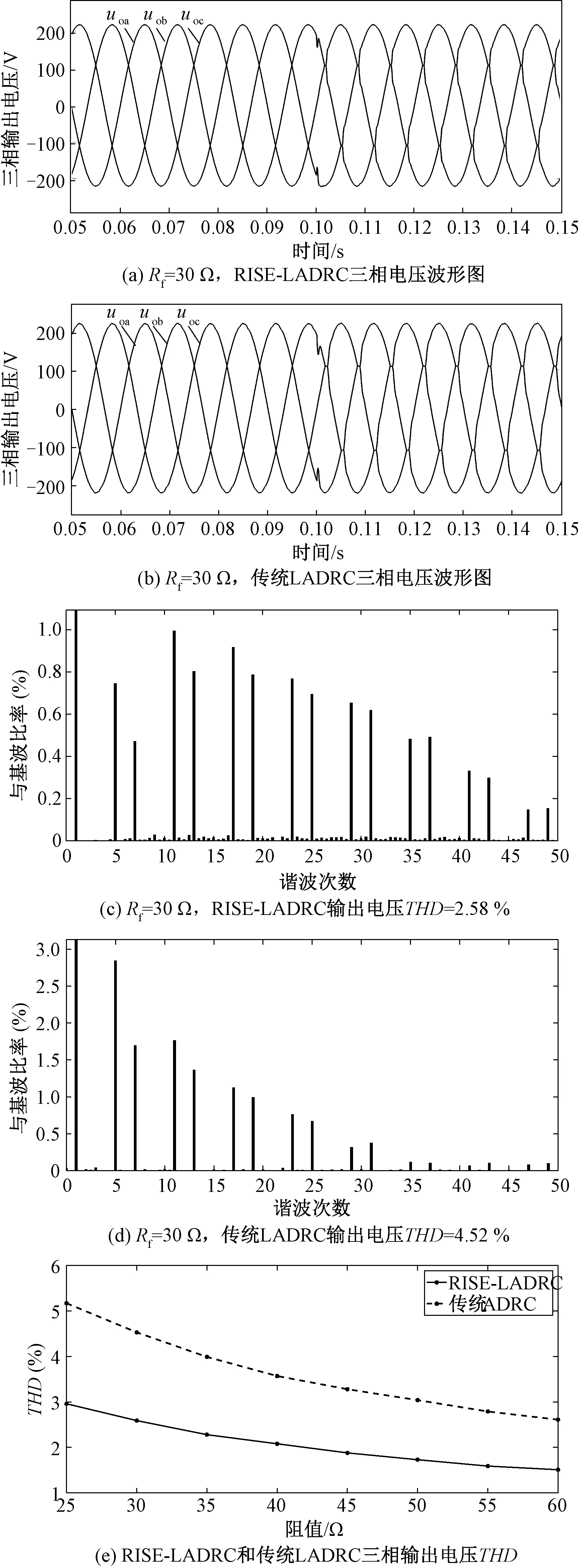
图6 接入三相非线性负载结果对比Fig.6 Comparison of results with three-phase nonlinear load

非线性负载Rf=30 Ω的情况下，图7(a)为两种控制策略下d轴输出电压响应时间图，其中，RISE-LADRC输出电压的响应时间为0.003 5 s，而传统LADRC的响应时间为0.015 s；图7(b)为两种不同控制策略下d轴输出电压的跟踪误差对比图，RISE-LADRC输出电压标幺值的波动范围为0.991～1.005 pu，传统LADRC输出电压标幺值的波动范围为0.982～1.015 pu。综上可知，RISE-LADRC的快速性更好、跟踪误差更小、跟踪精度更高。

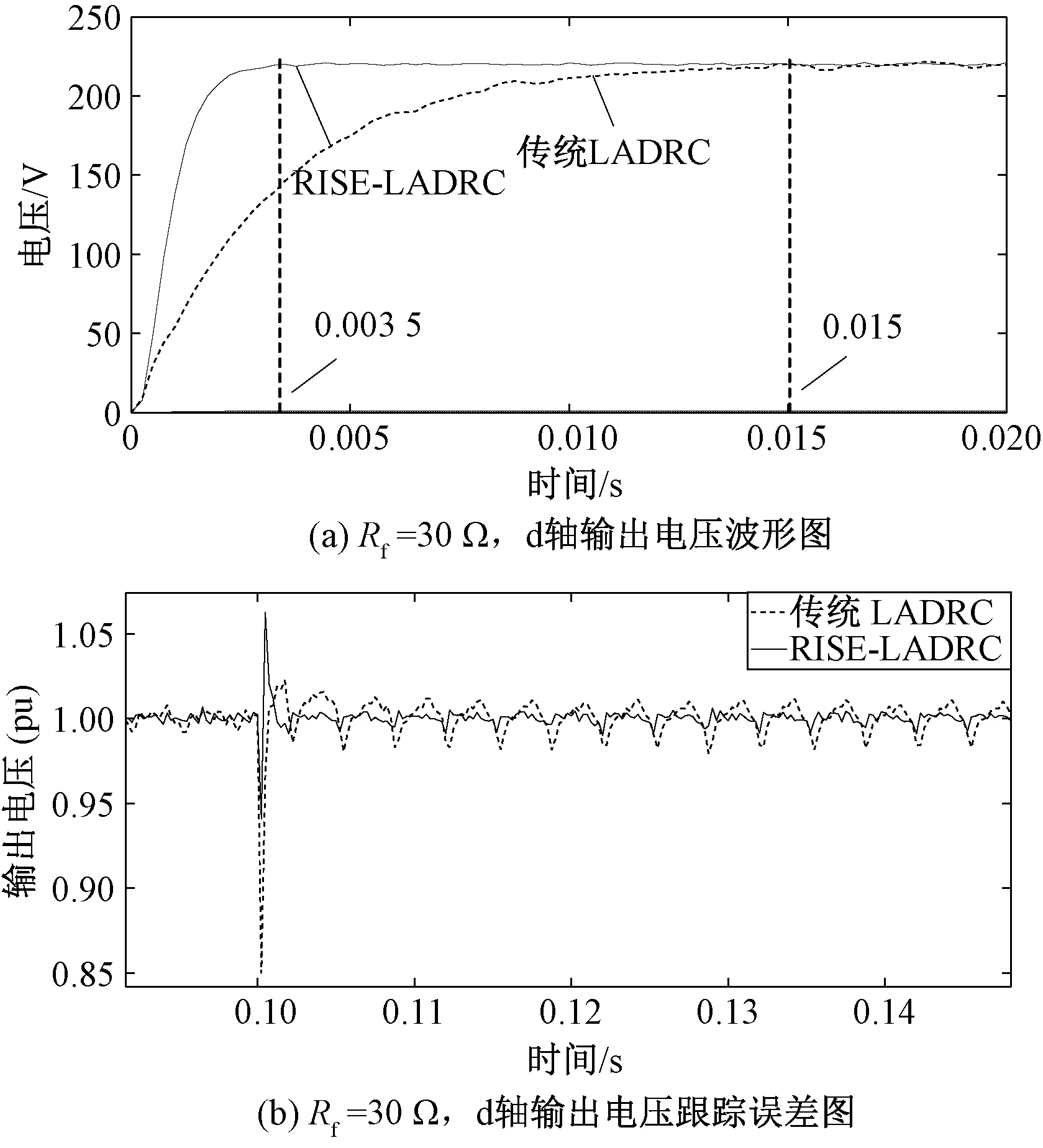
图7 非线性负载条件下动态性能图Fig.7 Dynamic performance graph under non-linear load conditions

5.2 实验验证

为了进一步验证所提控制策略的正确性和可行性，使用青铜剑科技公司实验设备搭建了LC型离网逆变器系统样机，如图8所示。逆变器系统采用三相全桥电路，硬件包括控制器、驱动保护电路和采样电路。实验控制芯片采用TI公司生产的TMS320F28335芯片，PWM波由TMS320F28335芯片的ePWM模块生成，主电路和控制器的参数与仿真保持一致。

图8 实验样机Fig.8 Experimental prototype

为了验证本文提出的RISE-LADRC控制策略对带不平衡负载扰动的抑制能力，在负载端接入50 %线性平衡负载，再在ac相跨接30 Ω电阻模拟不平衡负载，实验结果如图9所示。图9(a)、图9(b)分别为不平衡负载工况下的三相输出电压、电流波形。可以看出，在不平衡负载条件下，本文提出的RISE-LADRC控制策略能保证逆变器三相输出电压保持平衡。

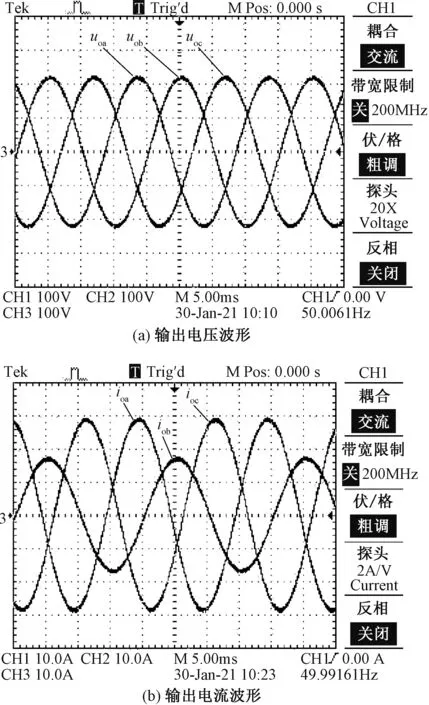
图9 带不平衡负载的输出电压、电流波形Fig.9 Output voltage and current waveforms with unbalanced load

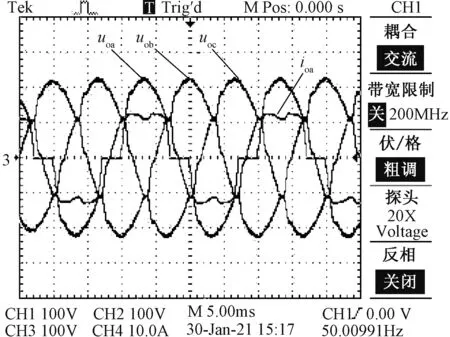
图10 带非线性负载的输出电压、电流波形Fig.10 Output voltage and current waveforms with nonlinear load

为了验证本文所提控制策略对带非线性负载扰动的抑制能力，在负载端接入三相整流桥，三相整流负载电阻为60 Ω，实验结果如图10所示。图10为三相整流非线性负载工况下的逆变器三相输出电压和a相输出电流波形，受非线性负载的影响，三相输出电压均发生畸变，本文提出的RISE-LADRC控制策略的电压波形THD为2.31 %。

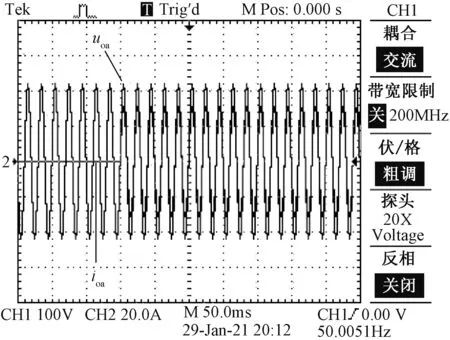
图11 线性负载由空载到满载的输出电压、电流波形Fig.11 Output voltage and current waveforms of linear load from no load to full load

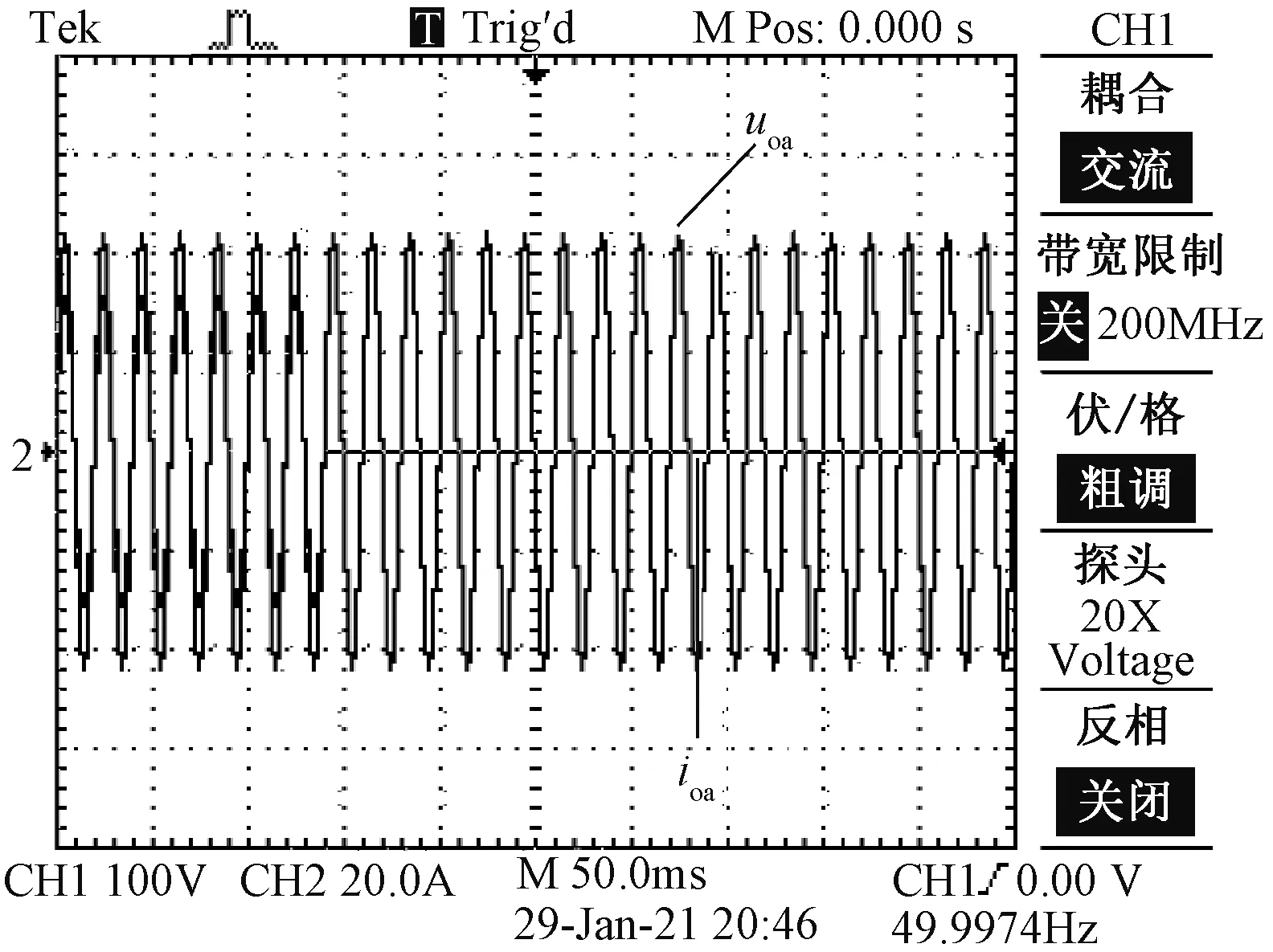
图12 线性负载由满载到空载的输出电压、电流波形Fig.12 Output voltage and current waveforms of linear load from full load to no load

图11和图12分别为逆变器线性负载从空载变化到满载、满载变化到空载时a相输出电压和电流波形，由此可知，所提控制策略在负载切换过程中输出电压大小基本保持不变，输出电流始终保持稳定，且无超调现象。

综上分析可得，在不平衡负载、非线性负载以及负载切换等扰动情况下，本文所提的控制策略表现出较好的抗扰能力。可以说明，所提控制策略能有效地加强扰动抑制能力，使得系统具有较好的抗扰性能，验证了本文提出的控制策略的可行性。

6 结论

当离网逆变器中出现不平衡负载和非线性负载等强扰动时，传统LADRC的抗扰能力不足，针对此问题，本文提出一种新型RISE-LADRC控制策略，其中LADRC和RISE都不依赖精确的数学模型。所提RISE-LADRC控制策略通过LESO实时估计系统中的总扰动，结合RISE控制有效地抑制扰动，提高系统的跟踪性能，并通过李雅普诺夫稳定性定理验证了系统的稳定性。在LESO观测带宽一定的情况下，对RISE-LADRC控制策略和传统LADRC控制策略进行仿真对比分析。仿真结果表明，系统中存在强扰动时，RISE-LADRC控制策略的输出电压畸变率更低，输出电压能准确地跟踪参考输入，达到稳态时的快速性更好，有效地降低了强扰动对跟踪性能的影响。因此，本文提出的RISE-LADRC控制策略具有更好的抗扰能力和动态响应性能。