考虑密封环材料属性和表面形貌干气密封启停阶段的动态接触特性分析

孙雪剑，宋鹏云，毛文元，邓强国，许恒杰，陈维

（1昆明理工大学化学工程学院，云南昆明 650500；2昆明理工大学机电工程学院，云南昆明 650500）

引 言

干气密封是离心式压缩机等旋转机械的主流密封装置，是起核心关键作用的零部件。在启动时，干气密封端面处于接触状态，当转速超过某临界值后，密封端面脱离接触。此外，在实际运行过程中，随着工况的波动或干扰的变化等，两密封环之间还可能发生接触摩擦。密封端面的接触可分为动态接触和静态接触。静态接触是静止状态下的接触或无扰动状态下的接触；动态接触则是运转状态下的接触，或存在扰动状态的接触。当扰动频率很小时动态接触可演变成静态接触。干气密封在启动和停车阶段或稳定运行过程中的碰摩动态接触[1-2]，大大降低了密封系统的稳定性和可靠性，甚至可能导致摩擦自激振动[3-4]，引起密封失效。因此探究干气密封的动态接触特性，对判断干气密封启停过程的稳定性及预测干气密封摩擦自激振动现象的发生发挥着重要作用。

关于干气密封动态过程研究，一些研究人员[5-7]对多种槽型干气密封进行了数值分析，研究了不同槽型结构参数对密封动态性能的影响，为干气密封的结构优化提供了依据。Chen等[8]通过搭建干气密封实验台，对螺旋槽干气密封的瞬态膜厚和泄漏率进行测试，验证了基于摄动法动态理论研究的有效性。随着干气密封向高压高转速的极端工况领域迈进，密封中气体介质的物理特性成为不可忽略的因素。多位研究人员[9-12]考虑气体的实际气体效应和阻塞流效应、惯性效应、滑移流效应等，分析了多种特殊气体效应对干气密封动态特性的影响。江锦波等[13]将超临界二氧化碳气体物性参数及流动状态等多变量进行耦合，分析了相关特性对超临界二氧化碳干气密封的动态刚度、阻尼系数的影响。当前关于干气密封动态特性的研究主要集中在微扰情况下气膜的动态特性，对于启停阶段密封环的动态接触特性研究还鲜见报道。

干气密封启停阶段的动态接触特性是在结合面微观接触理论的基础上开展的，当前微观接触模型主要分为分形接触模型[14-16]、统计学接触模型和有限元接触模型[17]。而统计学接触模型是认可度较高并广泛得到应用的接触模型。1966年Greenwood等[18]根据赫兹弹性接触理论提出了经典的GW接触模型，并指出表面形貌对接触特性有着很大的影响，该模型被广泛应用于机械密封接触特性的研究[19-21]。随后在GW模型的基础上考虑微凸体弹塑性变形的CEB模型[22]、KE模型[23]等经典接触模型被相继提出，并在机械密封领域得到应用[24-26]。然而对于微凸体弹塑性状态的判定，无论是CEB模型的最大接触压力达到材料硬度HB值的0.6倍时开始屈服，还是KE模型的平均接触压力等于材料屈服强度的2.8倍时进入全塑性变形，均是来自于Tabor对铝、铜、低碳钢等金属材料的球形压痕实验所总结出的结论[27-28]。干气密封的动静环常用硬（碳化硅陶瓷）-软（高强度石墨）的配对方式，碳化硅的硬度大于石墨，接触变形主要发生在石墨环。尽管大量石墨材料的性能测试实验[29-31]证明了石墨材料存在塑性变形，机理是物体被微观的裂缝所切割，整体不失去连续性，宏观上显示出塑性变形的特征，但石墨仍然是传统意义上的脆性材料。其弹性变形、塑性变形的临界参数与金属材料有一定的差别。因此密封环材料的属性和真实表面形貌不容忽视。

本文根据统计学接触理论和等效阻尼思想，考虑微凸体的弹性变形和塑性变形，通过石墨密封环在文献加载实验[32]中的应力应变特性对微凸体的临界变形参数进行修正，推导出适用于干气密封干摩擦界面的法向动态接触刚度和法向动态接触阻尼的解析模型。与此同时通过实验测得密封环真实表面形貌，确定接触模型的初始参数，探究干气密封端面发生接触时法向动态接触刚度和法向动态接触阻尼等参数的变化规律和影响因素。

1 端面接触模型确定

干气密封的基本结构如图1(a)所示。动静环配对有两种模式：一种是硬-硬配对；另一种是硬-软配对。常用的硬环材料是碳化钨硬质合金或碳化硅陶瓷，软环材料是高强度石墨。这里考虑常见的碳化硅和石墨配对情况，即硬-软配对。旋转环（动环）为碳化硅，非旋转环（静环）为石墨。密封环表面并非光滑平面，实际是由大量的微凸体所构成，如图1(b)所示，真实接触过程是微凸体之间的作用。动静环的半径尺寸并非相同，发生接触时名义接触面积以较小尺寸的静环为准，因此可以将其看成两个等半径的圆环，如图1(c)所示。

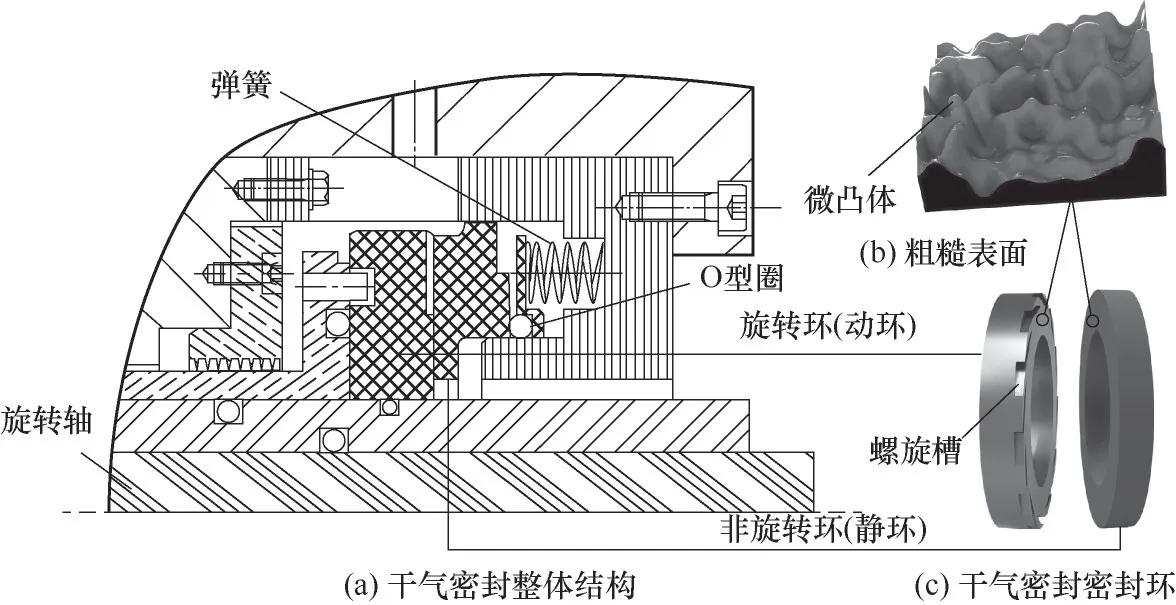
图1 干气密封结构及密封环微观表面Fig.1 The structure of the dry gasseal and the microscopic surface of sealing rings

1.1 单个微凸体接触参数

由于碳化硅的硬度大于石墨，接触变形主要发生在石墨环上。因此采用GT模型[33]假设，将结合面等效为光滑刚性平面和粗糙平面的接触，认为硬度较高的动环为刚性平面，硬度较低的静环为粗糙平面。在此基础上本模型基于以下几点假设：(1)微凸体之间相距较远，不考虑其相互作用；(2)摩擦副配对材料表面各向同性；(3)微凸体峰顶曲率半径相同；(4)接触过程基体不变形，仅有微凸体变形；(5)微凸体法向接触与切向摩擦相互独立。

两端面接触示意图如图2（a）所示。单个微凸体与刚性平面接触前后，半球形微凸体顶部发生变形情况如图2（b）所示。董沫辰等[32]对石墨环进行加载实验，并得获得了应力应变特性，如图2（c）所示，其中ε1为2.87%，ε2为3.26%。从实验结果发现，当应变ε<ε1时，法向应力和应变的关系是线性的，根据赫兹弹性理论[34]，此时认为密封环发生弹性变形；当ε2≤ε≤ε1时，应力不随应变而变化或者变化浮动较小，根据Abbott and Firestone塑性接触理论[35]此时发生塑性变形；当ε>ε2时，随着应变的增加，应力迅速下降，此时密封环发生明显断裂失效。

图2中z为结合面微凸体的高度；d为刚性平面与微凸体高度平均线的间距；h为刚性平面与粗糙表面高度平均线的距离；ys为微凸体高度平均线和表面平均高度线的距离；R为微凸体的峰顶曲率半径；单个微凸体法向变形量[18]：

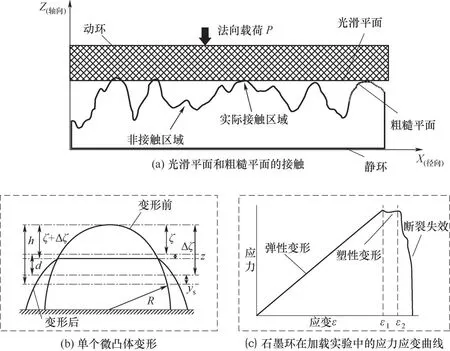
图2 干气密封端面接触及微凸体变形示意图[32,35]Fig.2 End face contact of the dry gas seal and deformation of asperity[32,35]

基于文献[32]实验结果，本文假设石墨环上单个微凸体的应力应变特性与石墨环整体的应力应变特性相同，即

其中，ΔL为密封环的法向变形量，L为密封环原始厚度，R为微凸体原始高度。弹性变形的临界法向变形量ζ1，塑性变形的临界法向变形量ζ2分别为：

单个微凸体在弹性接触阶段（ζ＜ζ1），根据赫兹弹性理论[34]，其平均接触压力Pt、接触面积At、静态接触刚度Kt公式如下：

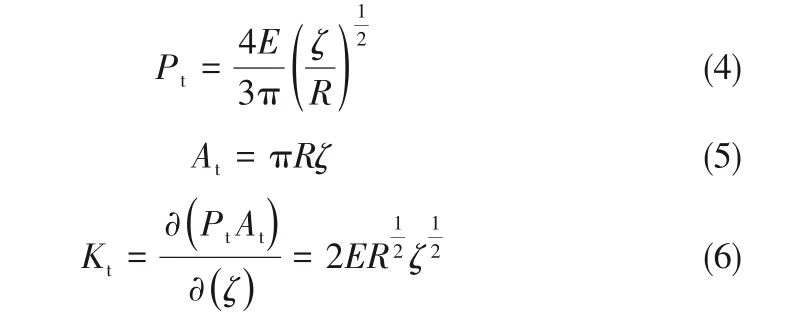
式中，E为等效弹性模量；当ζ2≥ζ≥ζ1时，微凸体从原来的弹性变形转变为塑性变形，单个微凸体在塑性变形阶段平均接触压力Ps为：

根据Abbott and Firestone塑性接触理论[35]，此时接触面积As为：

塑性变形微凸体静态接触刚度Ks为：

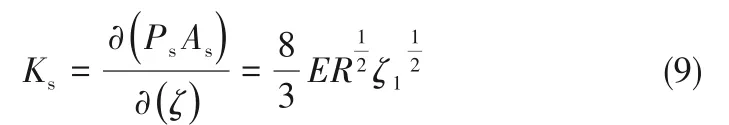
当ζ＞ζ2时，微凸体整体失去连续性变形，发生断裂失效，法向应力快速下降，表现出脆性材料的特性，这与金属材料有所不同。

1.2 干气密封实际接触界面参数

假设密封环表面的微凸体分布方式满足高斯分布，微凸体高度分布的概率密度表达式[18]为：

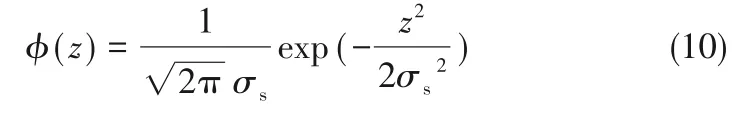
干气密封接触界面上微凸体数量为：

其中，η为单位面积上微凸体的面积密度，N1、N2、N3分别为密封环表面上发生弹性变形、塑性变形和断裂失效的微凸体数量。根据干气密封实际情况，接触压力应小于等于最大端面比压[36]，通过计算发现，发生断裂失效的微凸体数量小于微凸体总数量的0.073%。由于发生断裂失效的微凸体数量较少且力学特性较为复杂，参考金属材料微观接触特性的处理方法[35]。计算时将断裂部分的微凸体假设为塑性变形进行计算，即

其中，An为名义接触面积。密封环结构模型如图3所示，ri、ro为密封环的内外半径，rg为槽根处的半径，α为螺旋角，Ng为槽数，h0为开启后两密封环的间隙。当端面发生接触时，槽区部分并未接触，密封环名义接触面积An为非槽区面积。当槽台比为1时，An的表达式为：

图3 干气密封端面结构及密封环接触位置Fig.3 End face structure of the dry gas seal and contact position of seal rings

密封环接触界面的实际接触面积表达式为：

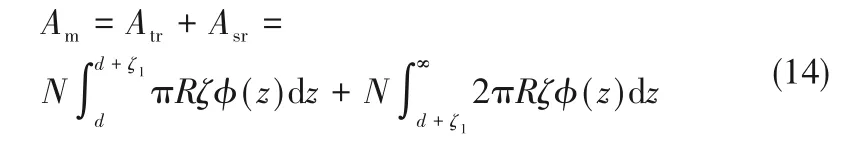
其中，Atr为弹性变形微凸体真实接触面积；Asr为塑性变形微凸体真实接触面积。密封端面接触力为：

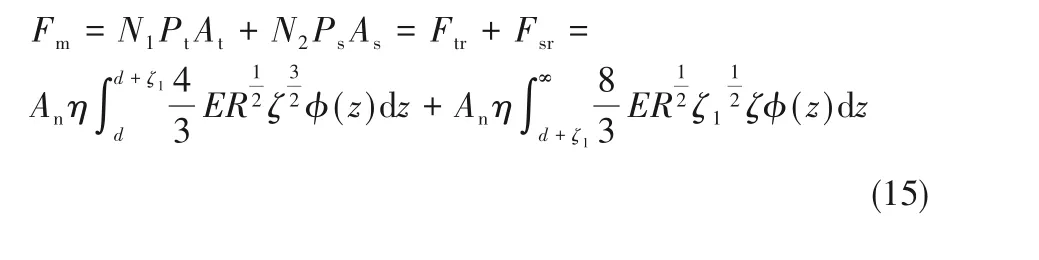
其中，Ftr为弹性变形微凸体实际接触力；Fsr为塑性变形微凸体实际接触力。密封端面静态接触刚度表达式为：

其中，Ktr为弹性变形微凸体静态接触刚度；Ksr为塑性变形微凸体静态接触刚度。

1.3 干气密封动态接触刚度模型

在密封环法向静态接触的基础上施加微小的位移扰动，此时产生的静态刚度和微扰刚度之和组成了法向动态接触刚度。但发生塑性变形的微凸体是不可恢复的，其平均接触压力不随法向位移ζ而变化[35]。因此塑性变形的微凸体无动态微扰刚度。整个结合面动态接触刚度是由弹性变形微凸体的动态接触刚度Kdr和塑性变形微凸体的静态接触刚度Ksr所组成。弹性变形微凸体某一时刻总变形量表达式为：

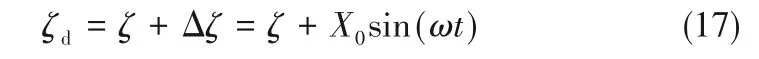
其中，X0sin(ωt)为动环简谐动态位移；X0为位移振幅；ω振动频率；T为振动周期；ω=1/T。根据泰勒展开式并略去二阶和高阶项，弹性变形的微凸体动态接触压力[37]为：

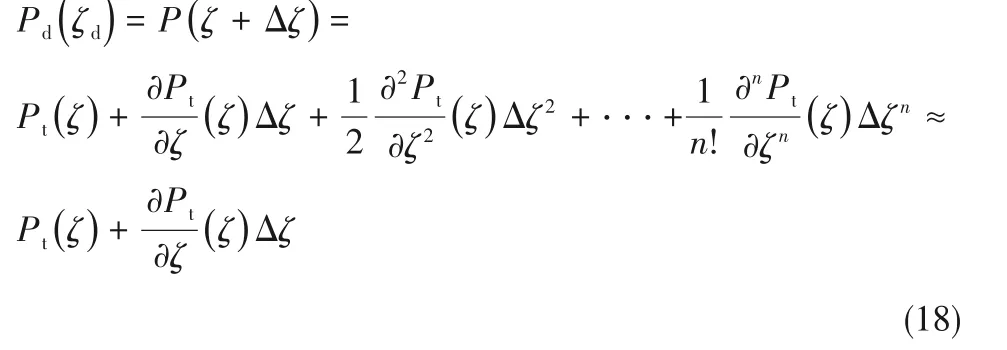
弹性变形的微凸体动态接触刚度为:

干气密封实际接触界面在一个简谐振动周期内的平均动态接触刚度为：

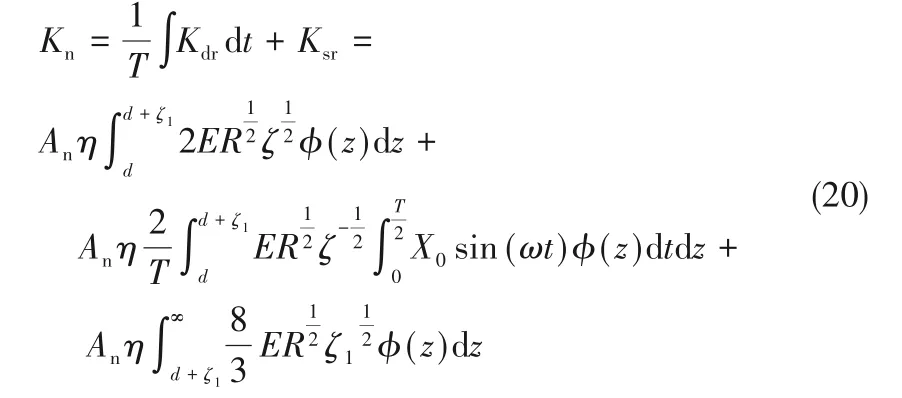
1.4 干气密封动态接触阻尼模型

干气密封接触界面的法向等效黏性阻尼[38]，即在一个激振周期内微凸体经历了加载和卸载的过程，弹性变形的微凸体卸载后可以完全恢复，而塑性变形的微凸体则无法恢复，转化成能量消耗。这种能耗机理是产生结合面接触阻尼的主要原因。根据等效阻尼思想其机械能表达式[39]为：

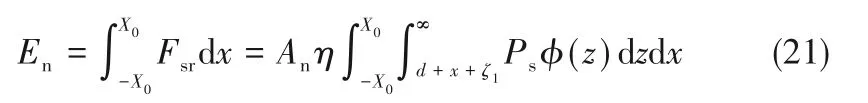
其中，En为塑性微凸体变形消耗的机械能。动态接触阻尼表达式[37]为：

2 实验确定接触表面形貌参数

统计学接触模型是在微观表面形貌基础上建立的，不同界面的表面形貌对接触特性的影响有着很大差别，为了探究干气密封接触界面的真实特性，采用表面轮廓仪对动静环表面形貌进行实际测量。

2.1 粗糙表面统计学参数表达理论

干气密封动静环表面形貌检测原理是根据McCool[40]提出的理论，通过测得粗糙表面轮廓的均方根偏差Rq和均方根斜率差Rdq来表征粗糙表面的轮廓谱函数，然后通过表面的轮廓谱函数求出轮廓谱函数的谱矩，进而求出密封环真实形貌下的统计学参数，表面轮廓的谱函数s(l)为：

其中，l为各种表面粗糙峰（轮廓高度）出现的频率；τ称为谱指数[41]；c为比例常数(通过零、二阶谱矩联立求得)；粗糙表面轮廓谱函数s(l)的n阶谱矩表达式为：

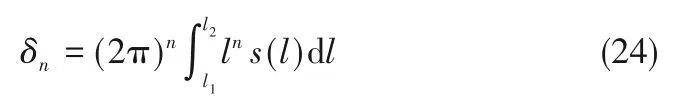
其中，l1为表面轮廓高度分布的较低频率，l1=1/jr=0.004μm-1；l2为表面轮廓高度分布的较高频率，是由表面轮廓仪的触针半径确定，l2=1/r=0.5μm-1。将式(23)代入式(24)中，可得到粗糙表面轮廓谱函数的零阶矩δ0、二阶矩δ2和四阶矩δ4的表达式[40]。表面轮廓仪可以测量密封环端面的轮廓均方根偏差Rq和均方根斜率差Rdq，它们与粗糙表面轮廓谱函数的零、二阶矩（δ0和δ2）有关。

其中，轮廓均方根偏差Rq也常用σ进行表达。通过实验获得Rq和Rdq的测量值，则动、静环粗糙表面轮廓谱矩之和为：

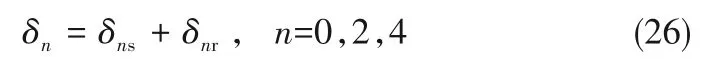
式中，下角标s和r分别代表静环和动环。通过式（26）求得表面轮廓谱零阶矩δ0、二阶矩δ2和四阶矩δ4，进而可以得到刚性平面与微凸体高度平均线的间距d[42]、带宽参数α[42]、微凸体高度平均线和轮廓表面平均高度线之间的距离ys[42]、粗糙表面微凸体高度分布的标准差σs[20]、微凸体峰顶曲率半径R[42]和微凸体面积密度η[43]等相关参数，分别为：

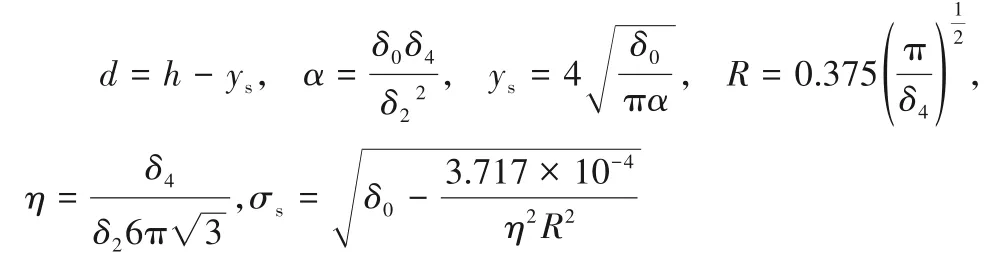
其中，R、η是统计学接触模型中的重要参数[18]。

2.2 实验测试及结果

图4（a）为表面轮廓仪对密封环表面形貌参数的测试装置及曲线，实验设备为粗糙度轮廓仪测定一体机(SEF680)，测量范围Z=50 mm，X=100 mm，其触针半径r为2μm，取样长度jr为0.25 mm。

实验静环材质为碳石墨，动环材质为碳化硅。设置测定速度0.2 mm/s、评估长度jn=5jr=1.25 mm。在静环和动环端面上随机选择10个位置，每个位置测两次后取平均值，得到静环和动环表面粗糙度的典型轮廓曲线如图4(b)所示。测得动静环表面10个不同位置的表面轮廓均方根偏差Rq和均方根斜率Rdq数据及相关文献数据[21]如表1所示。从表中可以看出，当前实验数据与文献数据最大相对误差仅为8.47%，整体较为吻合。数值上的偏差是因为密封环微观表面并非均匀，测试位置不同结果会略有不同。因此需要多组数据取平均值的方法来降低因测量带来的误差。

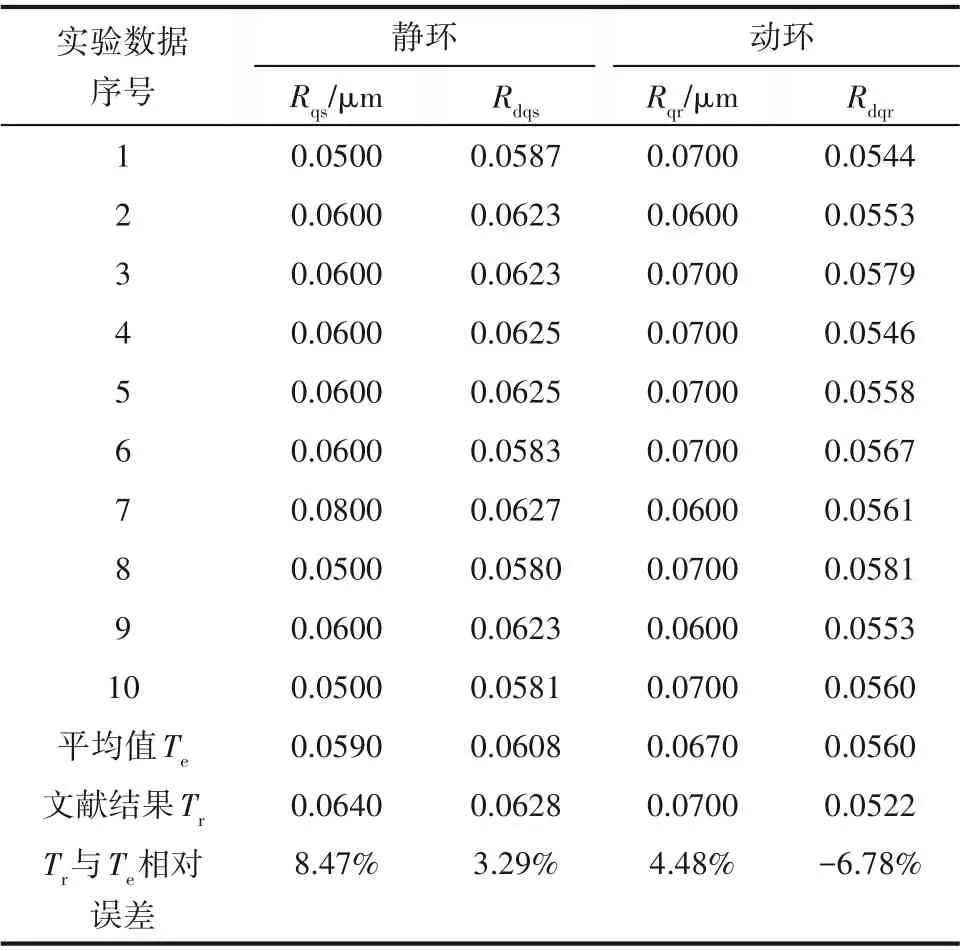
表1 均方根偏差和均方根斜率差的实验数据Table 1 Experimental data of root mean square deviation and root mean square slope

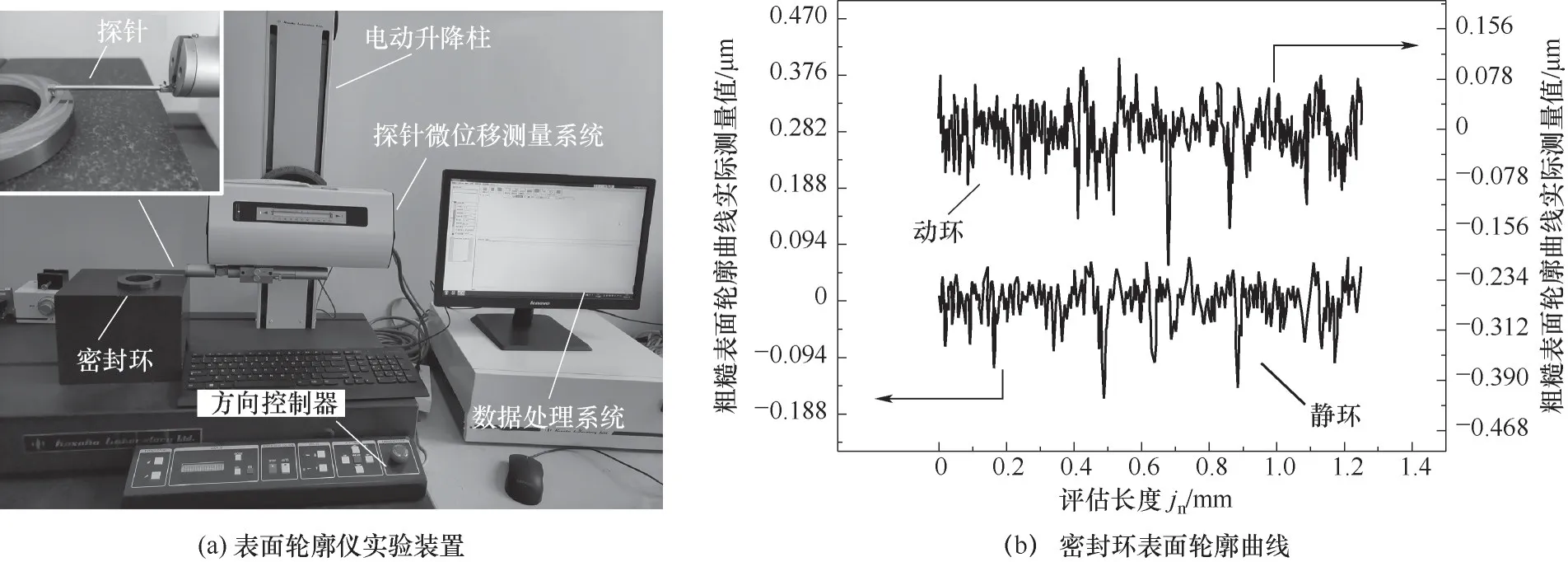
图4 实验测试装置及表面轮廓测试曲线Fig.4 The experimental device and the test curve of surface profile

3 结果讨论与分析

干气密封环材料特性参数和密封环几何尺寸参数[44-46]如表2所示。

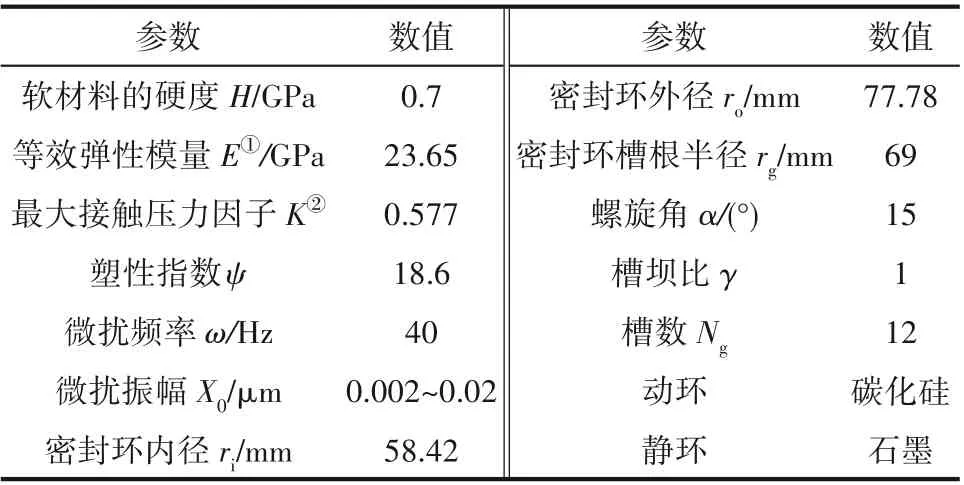
表2 计算模型结构参数和材料参数Table 2 Structure parameters and material parameters of the model

3.1 模型验证

端面接触力是接触性能分析的重要参数，无论动态接触刚度还是动态接触阻尼均是在接触力的基础上求解的。为了验证本文模型的准确性，对当前模型接触力计算结果与经典接触模型[18,22-23,47]结果进行对比，其中经典模型所需的初始参数值如塑性指数、最大接触压力因子等来自于表2。各模型整体变化趋势如图5所示。可见本文结果与各经典模型整体趋势一致，且与GW模型更为接近。这也验证了McCool[43]的结论，即GW模型对脆性材料接触特性的判断有较好的准确性。

图5 接触力模型正确性验证Fig.5 Model verification of contact force

3.2 端面接触比压对动态接触特性的影响

在干气密封启停阶段，端面接触比压Pb（单位名义接触面积的接触压力），即密封端面接触力Fm与端面名义接触面积An的比值，是端面承载能力的重要组成部分，端面接触比压的变化直接影响动态接触特性。基于典型干气密封端面比压范围[36]，进行其影响动态接触特性规律分析。刚性光滑平面与粗糙表面高度平均线之间的距离h、实际接触面积Am随接触比压Pb的变化特性如图6所示。h随接触比压的增大而变小，当接触比压较小时h的变化幅度较大，随着接触比压增大，h变化幅度减小。这是因为两密封环刚开始接触时，发生接触的微凸体个数较少，单个微凸体所受的法向接触比压较大，因此整体变形较为明显；随着接触比压增加，发生接触的微凸体个数增多，受力分散整体形变减缓。接触比压增大，导致发生变形的微凸体数目增多，进而接触面积随之增大。微凸体峰顶曲率半径是判断接触特性的重要指标，曲率半径较小时微凸体抵抗接触比压的能力较弱，容易产生较大的变形，此时微凸体更容易进入塑性变形；曲率半径较大时，微凸体抵抗变形能力随之增强，塑性变形开始减少。其中R=1.707μm来自于文献[25]，R=3.655 μm为本文实验结果。从图中可以看出刚性光滑平面与粗糙表面高度平均线之间的距离h和实际接触面积Am均随曲率半径增大而增大。

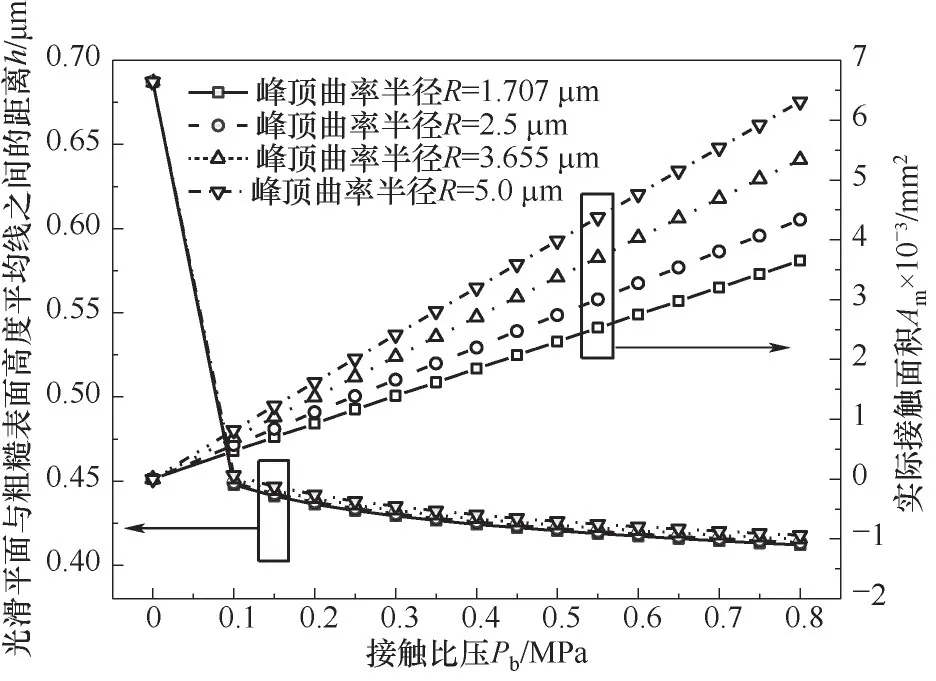
图6 接触比压对光滑平面与粗糙表面高度平均线之间的距离h和实际接触面积Am的影响Fig.6 The effect of contact pressure on separation based on surface heights(h)and real contact area(Am)

图7（a）为微扰频率ω=40 Hz、微扰振幅X0=0.02 μm时，密封环端面法向静态接触刚度和动态接触刚度随接触比压变化特性图。静态接触刚度和动态接触刚度均随接触比压、曲率半径的增大而增大。相同曲率半径条件下的法向动态接触刚度和静态接触刚度整体变化趋势较为接近，说明接触比压对动静态接触刚度的影响远大于曲率半径的影响。为了更好地观察法向动静态接触刚度的不同，将相同接触比压条件下，动静态刚度的差值绘制如图7（b）所示。动、静态接触刚度之间的差值随接触比压和曲率半径的增大而增大。当微凸体曲率半径较大时，微凸体抵抗变形能力较强，接触状态以弹性变形为主，动态刚度的增量较大。当曲率半径较小时，微凸体抵抗变形的能力较弱，部分微凸体进入了塑性变形，此时的微凸体只有静态刚度[35]，因此动、静态刚度差减小。

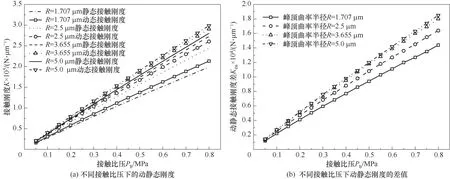
图7 接触比压对动静态接触刚度的影响Fig.7 The effect of contact pressure on dynamic contact stiffnessand static contact stiffness

干气密封法向动态接触阻尼随接触比压的变化特性如图8所示。法向动态接触阻尼随接触比压的增大而增大，其增长速率随曲率半径的减小而增大。当曲率半径为5.0μm时，阻尼非常小，且接触比压对其的影响较弱。这是因为曲率半径较大时，端面接触绝大部分为弹性变形，在加载和卸载的过程中，弹性变形的微凸体几乎可以完全恢复，并没有能量的损耗，进而阻尼趋于零。随着曲率半径的减小，微凸体表面由弹性变形向塑性变形转变，这会导致塑性变形的微凸体无法卸载还原，产生能量的消耗，进而产生接触阻尼。随着接触比压增大刚性平面与粗糙表面的间隙变小，接触界面的微凸体数目增多，消耗的能量增大，阻尼也随之增大。

图8 接触比压对动态接触阻尼的影响Fig.8 The effect of contact pressure on dynamic contact damping

干气密封启停阶段处于变转速工况，根据干气密封运行特点，该阶段密封环间距随转速的升高而增大，随转速的降低而减小。转速的变化直接影响密封环间距的变化，进而影响动态接触特性的变化。启停脱开转速膜厚对动态接触特性的影响规律如图9所示。可以看出，当转速为零时，密封环间距最小，接触比压最大，此时参与接触的弹性微凸体和塑性微凸体的数目最多，进而导致此时动态接触刚度和接触阻尼为整个阶段的最大值，随着转速的升高，密封环间距开始增大，参与接触的微凸体数目开始减少，动态接触刚度和接触阻尼呈类指数下降，当超过50%临界脱开转速膜厚时，动态接触刚度和阻尼变化极其微弱，原因在于随着密封环间距的增大，微凸体接触数目减小，只有较高的微凸体参与接触，当前模型认为端面微凸体高度呈高斯分布，虽然存在较高的微凸体但数目极其少，因此超过50%临界脱开转速膜厚时动态接触特性变化微弱。由此可见，在脱开转速膜厚对动态接触特性的影响中，需重点考虑前50%临界脱开转速膜厚。

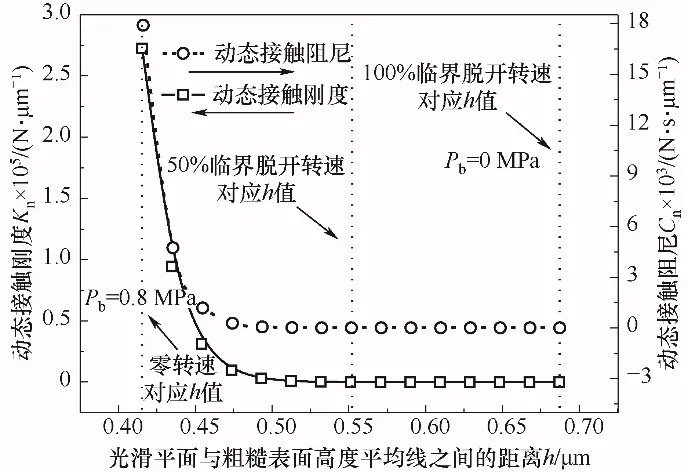
图9 脱开转速膜厚对动态接触特性的影响Fig.9 The filmthickness of separation speed effect on dynamic contact

3.3 表面形貌参数对端面动态接触特性的影响

图10为动态接触刚度、阻尼随表面形貌参数的变化特性，其中面积密度η、微凸体高度平均线和表面轮廓平均高度线的距离ys的参数范围参考文献[25]及当前实验结果。从图中可以看出，动态接触刚度和动态接触阻尼随面积密度η、微凸体高度平均线和表面轮廓平均高度线的距离ys的增大而增大，但两者单位在同一量级时，动态接触刚度的变化更为明显，接触阻尼的变化显得微乎其微，这也间接证明了当前整个结合面以弹性接触为主，微扰情况下端面的动态特性以动态接触刚度为主。ys的增大意味着刚性平面与粗糙平面的距离变小，此时微凸体的接触数目增多，与此同时一些原来发生弹性变形的微凸体转化成塑性变形，这导致了动态接触刚度和阻尼的同时增大，如图10（b）所示。粗糙度Ra[48]是表面形貌中的重要参数，对于高斯粗糙表面有σ=1.25Ra[49]，表面轮廓均方根偏差σ某种意义上可以表示接触表面的粗糙度Ra，参考机械工业标准《干气密封技术条件》（JB/T 11289—2012）中要求硬环表面粗糙度Ra不大于0.1μm，软环表面粗糙度Ra不大于0.2μm的原则，选取σ小于0.25μm的范围分析其对动态接触特性的影响，如10（c）所示。从图中可以看出，动态接触刚度和接触阻尼随表面轮廓均方根偏差的增大呈类指数增长，其中动态接触阻尼增幅更为明显。这是因为σ越大表面粗糙度Ra越大，接触界面微凸体的峰谷差越大，相同的接触比压情况下微凸体更容易发生塑性变形，进而导致了动态接触阻尼的增大。

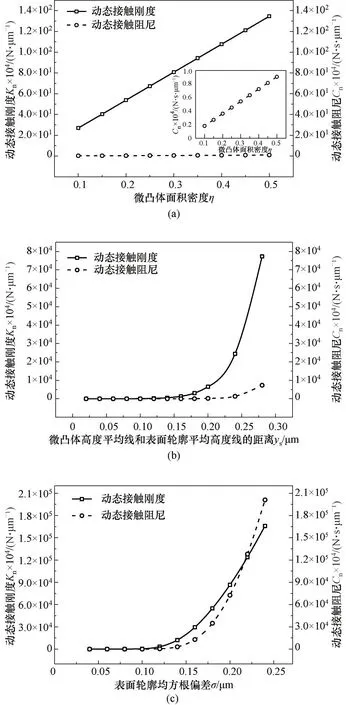
图10 表面形貌参数对动态接触刚度、阻尼的影响Fig.10 The effect of surface-topography parameterson dynamic contact stiffness and dynamic contact damping

3.4 振幅和频率对端面动态接触特性的影响

法向动态接触刚度和接触阻尼随扰动频率、振幅和接触比压的变化如图11所示。从图中可以看出，法向动态接触刚度随振幅、接触比压的增大而增大，随频率的变化并不明显。由此可以发现扰动振幅和接触比压对法向动态接触刚度的作用效果远大于扰动频率的作用效果。振幅增大导致了微扰位移增大，接触比压随之增大，进而导致了动态接触刚度的增大。而刚度本身是反映材料抵抗变形的能力，它与接触比压和位移成正比。对于动态参数对接触阻尼的影响，从图11（b）中可以发现接触阻尼随接触比压的增大而增大，随振幅的增大而减小，随频率的增大呈现出先减小后趋于平稳的特点。通过式（22）可知，影响动态接触阻尼变化的参数主要有机械能En、扰动振幅X0和扰动频率ω。当振幅X0、频率ω不变时，动态接触阻尼随En的增大而增大；当机械能En、振幅X0不变时，动态接触阻尼随频率ω的增大而减小；当机械能En、频率ω不变时，动态接触阻尼随振幅X0的增大而减小。接触比压增大时发生塑性变形的微凸体增多，消耗的机械能增大，但不影响频率和振幅的变化，因此出现动态接触阻尼随接触比压的增大而增大。当振幅增大时，发生塑性变形的微凸体数量增加，因此消耗的机械能增大，这导致振幅X0和机械能En同时增大，最终阻尼的变化取决于En、X0的变化速度。针对碳化硅-石墨构成的接触界面，动态接触阻尼随振幅的增大而减小，但不代表所有的材料均是如此，不同的材料表现出不同的阻尼特性。当频率增大时，一个激振周期消耗的能量不会发生变化，振幅也不随之变化，因此出现动态接触阻尼随频率的增大而减小。

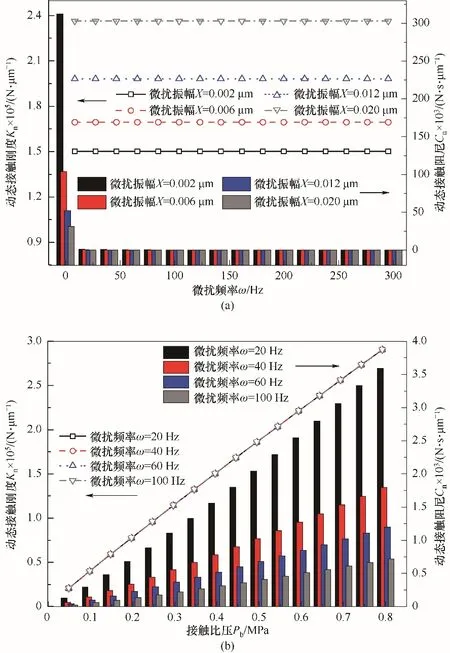
图11 动态参数对动态接触刚度、阻尼的影响Fig.11 The effect of dynamic parameters on dynamic contact stiffness and dynamic contact damping

4 结 论

在确定密封环接触端面真实表面形貌的基础上，考虑密封环材料属性，结合统计学接触理论和等效阻尼思想，推导出适用于干气密封干摩擦界面法向动态接触刚度和法向动态接触阻尼的解析模型，进行数值分析得到以下结论。

（1）法向动态接触刚度随接触比压、振幅的增大而增大。频率对动态接触刚度的作用效果远小于接触比压或振幅对接触刚度的作用。动、静态接触刚度随接触比压的变化趋势一致，但数值上存在一定的偏差，这种偏差随接触比压的增大而增大。

（2）动态接触阻尼随接触比压的增大而增大，随频率的增大而减小。振幅的增大导致结合面消耗的机械能En增大，接触阻尼随振幅的变化取决于消耗的机械能En和振幅X0的变化速度，针对碳化硅-石墨构成的接触界面，动态接触阻尼随振幅的增大而减小。

（3）与多个经典接触模型对比，本文的计算结果与经典的GW模型更为接近。针对干气密封碳化硅作为动环、石墨作为静环的配对方式，结合面的微扰动态特性以动态接触刚度为主。针对启停过程密封环发生的法向接触振动，主要考虑动态接触刚度对振动特性的影响，而动态接触阻尼较小，可以忽略。

（4）50%临界脱开转速之前的动态接触刚度和接触阻尼变化明显，超过50%临界脱开转速时动态接触特性变化微弱。法向接触特性的变化主要考虑50%临界脱开转速之前的接触阶段。