木榫旋转焊接抗拉拔力的影响因素响应曲面分析∗

张 剑 朱 海 陈家瑞 刘瑞丰

（1.东北林业大学机电工程学院，黑龙江 哈尔滨 150040;2.深圳市美好创亿医疗科技有限公司，广东 深圳 518116）

现代家具制造中广泛采用胶黏剂与五金件实现木材的连接[1]。但以石化产品为原料的胶黏剂不仅成本高，固化时间长，而且在使用过程中会产生有毒物质。五金件在使用过程中易受环境影响，会发生锈蚀等现象，影响其使用性能。木材旋转摩擦焊接技术[2]，通过木制构件在压力作用下相互摩擦，在几秒钟内产生较高温度，木材细胞聚合物受热分解成木材纤维素单体粘性混合物，摩擦停止后这种粘性界面材料在压力作用下凝固硬化[3]，从而实现木材的连接。这种无胶黏剂的连接方式可使连接强度达到木材结构应用所能达到的承载能力，而且理论上采用合适的焊接参数与条件，任何木材都可实现焊接。木材旋转焊接技术具有生产效率高、无环境污染、可保留木材美观性等优点，为现代家具制造和古典家具修复提供了新的思路与方法。国内外众多学者基于当地树种开展了一系列的研究[4-23]，从最初的小试件试验，到后来开发专用的焊接设备[3,22-23]。Rodriguez等[24]利用2 种加拿大硬木树种进行实验，评估了不同因素对木材焊接带力学强度的影响，观察界面接触区的扫描电镜照片，结合其他试验研究，认为木榫棒旋转焊接的焊接带界面层连接性能更多取决于木榫材质，焊接带界面层材料大多来自于木榫；焊接时采用材质硬度较低的基材并配以材质硬度较高的木榫棒，可相对提高焊接界面强度。朱旭东[25]等选取落叶松为基材，采用CuCl2浸渍后的桦木木榫，研究CuCl2处理对木榫焊接性能的影响。结果表明：经CuCl2处理的木榫能明显提高焊接界面的抗拉拔力。

响应曲面法(RSM)是一种新型的试验分析方法[26]，其中的Box-Behnken设计方法(以下简称BBD法)可以构建对已知因素与试验结果的回归分析[27]，构建相应的数学模型，最终获得试验因素与结果之间的影响规律，响应面法具有更高的回归精度，在残差弯曲的基础上可以获得精细的二次方回归方程[28]。

本研究采用东北地区特色树种樟子松(Pinus sylvestrisvar.mongolicaLitv.)进行木榫旋转焊接试验，采用响应面试验分析方法，系统研究进给速度、转速、榫径/孔径比对抗拉拔力影响规律，并建立几种影响因素与抗拉拔力间的数学关系，进而得到最佳焊接参数组合，提高焊接的可靠性。

1 材料与方法

1.1 材料

试验采用相同树种的基材与榫棒，选用东北地区特色树种樟子松，实验材料取自黑龙江省牡丹江林区。基材试件尺寸为长40 mm、宽40 mm、高100 mm，纹理方向为顺纹，预钻孔直径8 mm、深度45 mm，焊接深度30 mm。榫棒直径规格分别为10、11、12 mm，榫棒长度为100 mm，榫棒前端设置倒角。试件含水率调节8%～12%。

1.2 设备

数控铣床，VH-850，台湾绮发机械工业股份有限公司；万能力学试验机，Byes-2003，邦亿精密量仪（上海）有限公司。

1.3 试验方法

将表面有预钻孔的基材固定在台钳上，焊接前清理基材表面及预钻孔内的木屑，用铣刀夹具将榫棒夹紧，预紧力不要过大避免造成榫棒破坏。

木材焊接受诸多因素影响，除树种、含水率等木材本身性质的影响外，还受进给速度、转速、榫径与孔径差异等因素的影响。本文以进给速度、转速、榫径/孔径比为研究的主要变量，采用BBD法研究工艺参数对焊接抗拉拔力的影响。选用Design-Expert8.0 软件进行响应面试验分析处理。

焊接试验参数如表1 所示，试验安排参照三因素三水平的响应面试验计划表，共计17 组试验，每组试验重复3 次。

表1 响应面试验因素与水平表Tab.1 Factor level table of response surface test

焊接后试件在万能力学试验机上进行拉伸试验，测量焊接抗拉拔力。拉伸试验的加载速度为5 mm/min，直至榫棒被完全拔出。

2 结果与分析

2.1 响应面结果分析

根据BBD法基本要求进行试验，通过预实验得到较好工艺参数，利用Design Expert 8.0 软件生成试验表格，得到相应参数下的抗拉拔力，试验方案及结果如表2 所示。

表2 Box-Behnken 响应面试验设计和抗拉拔力测试结果Tab.2 Box-Behnken Design of response surface test and test results of tensile strength

利用软件Design Expert 8.0 对试验数据进行二次多项式回归及拟合，得到以抗拉拔力为响应值，进给速度（A）、转速（B）和榫径/孔径比（C）为自变量的三元二次回归方程，如式（l）所示:

对试验结果进行方差分析，结果如表3 中所示。

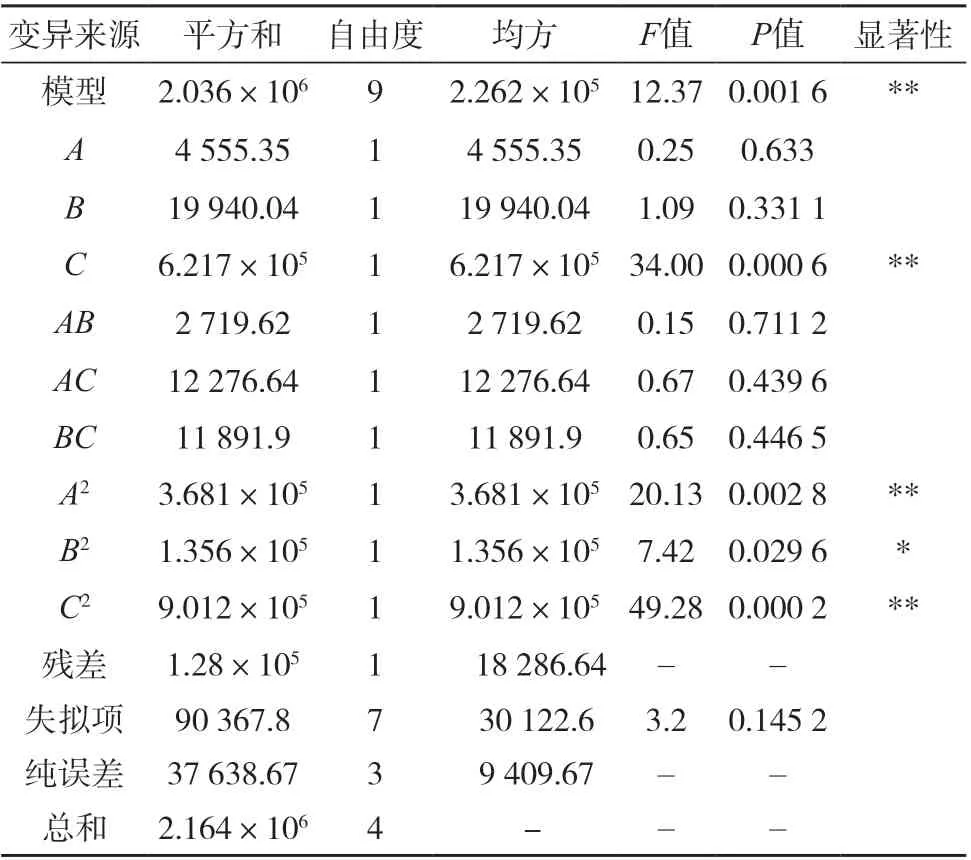
表3 Box-Behnken 响应面试验方差分析结果Tab.3 Box-Behnken variance analysis results of response surface test

由表3 可见，拟合P值为0.001 6，小于0.05，说明拟合结果具有显著性。单因素方面，榫径/孔径比(C)的P值为0.000 6，小于显著性水平0.05，影响显著，而进给速度(A)、转速(B)均大于0.05，其影响不显著，分析表明：在上述3 个工艺参数中，榫径/孔径比对抗拉拔力的影响作用最大，单因素对抗拉拔力影响作用的显著程度排序为榫径/孔径比(C)＞转速(B)＞进给速度(A)。交互项方面，三者的P值均大于0.05，说明3 种因素的交互作用对抗拉拔力的影响不大。二次项方面，A、B、C的二次项P值均小于0.05，具有显著性差异，表明各因素对试验抗拉拔力并非一般的线性影响。模型的失拟项P＞0.05，说明该模型的回归方程具有较好的拟合度和可信度，试验误差相对较小。

图1 为抗拉拔力回归响应模型的残差正态分布图和试验值与预测值的对应分析。残差正态分布图和试验值与预测值的对应情况可有效反映模型的实际关联程度。图1a试验中残差分布基本呈线性分布，说明残差以正态分布在试验中，表明模型可准确呈现各因素的影响规律和彼此的交互作用。图1b为模型对试验值和预测值的对比图，试验值与预测值均匀分布在一条斜线两侧，反映了模型预测的准确性较高。

2.2 响应面模型分析

响应曲面等高线图反映了各影响因素之间的交互作用，图2显示了固定某一工艺参数时，另外两个参数共同作用下对抗拉拔力的影响，如图2a、b、c。

图2 等高线图Fig.2 Contour map

分析图2响应面等高线，越接近圆形交互因素越不显著。由图可知，交互因素的响应面曲线均接近圆形，未表现为显著时的椭圆形，其交互因素影响均为不显著，与之前方差分析中的结论相一致。但当交互因素中含有榫径/孔径比时，图像表现出了更大的波动性，也证明了榫径/孔径比大小对最终的抗拉拔力有较大影响，其影响程度远远大于其他工艺参数。

2.3 抗拉拔力影响参数优化

通过对工艺参数三元二次回归方程的优化求解，确定了最优的抗拉拔力参数，结果接近于进给速度16 mm/s，转速3 000 r/min，榫径/孔径比为1.5。根据等高线分析，分布规律也基本吻合。因此，按回归方程极值选取的最优工艺参数组合进行木榫旋转焊接验证，结果如表4所示。

表4 木榫旋转焊接最佳工艺参数Tab.4 Optimum process parameters of wood dowel welding

从表4可以看出，按表中工艺参数进行试验后得到的抗拉拔力与预测优化结果十分接近，抗拉拔力误差仅为2%。 表明回归模型及优化具有较高的精准性。

3 结论

采用樟子松进行了同树种的圆棒榫旋转摩擦焊接试验，利用BBD法进行了进给速度、转速、榫径/孔径比对抗拉拔力影响规律试验研究，结果表明：在进给速度、转速、榫径/孔径比中，抗拉拔力的单因素影响显著性排序为榫径/孔径比＞转速＞进给速度。对响应面试验结果进行方差分析，模型整体拟合情况良好。建立并验证以抗拉拔力为响应值的数学模型，其优化后焊接工艺参数组合为进给速度16 mm/s，转速3 000 r/min，榫径/孔径比为12/8，在此条件下产生的抗拉拔力为2 197.4 N，模型具有较高的准确性。