一种基于聚类算法的卫星组合加工技术

臧梓轶 程 泽 蔡朝阳

一种基于聚类算法的卫星组合加工技术

臧梓轶 程 泽 蔡朝阳

（北京卫星制造厂有限公司，北京 100094）

以通信卫星太阳翼及天线接口组合加工领域为研究背景，分析了当前加工方法的弊端。首先基于图元分析，对加工过程进行增强模拟，利用空间坐标系转换原理构建加工坐标系与卫星坐标系的转移矩阵，实现加工策略的整体输出。在路径规划方面，提出了“一种基于聚类算法的加工路径规划方案”，通过随机初始化聚类中心、“距离”判断、自动分类、矢量长度累积求和等一系列流程，实现了最优加工路径的规划。在该方法中，加工路径与迁移路径均由计算机规划，减少了人工干预，提高了效率与预测的准确度。为后续实现智能化、自动化奠定了理论基础。该方法在卫星型号上得到验证，加工精度达到国内先进水平。

通信卫星；图元分析；聚类算法；路径规划

1 引言

通信卫星是卫星通信系统的空间部分，实现卫星通信地球站之间或地球站与航天器之间的通信。以某型号东四平台通信卫星为例，其主体构型是一个2100mm×3600mm×2360mm的长方形箱体，由平台结构和通信舱结构组成，另外还有作为次级结构件的一套东馈源支撑结构以及一块馈源防护板。整个结构分系统的组成示意图见图1。平台结构又分为推进舱和服务舱。其中，推进舱由中心承力筒、490NG发动机支架、中板、背地板、推进舱南北隔板和东西隔板组成；服务舱由服务舱南北板组成。通信舱由对地板、通信舱南北板和通信舱南北隔板组成。东馈源支撑结构由馈源安装板、±竖隔板和加强板组成。

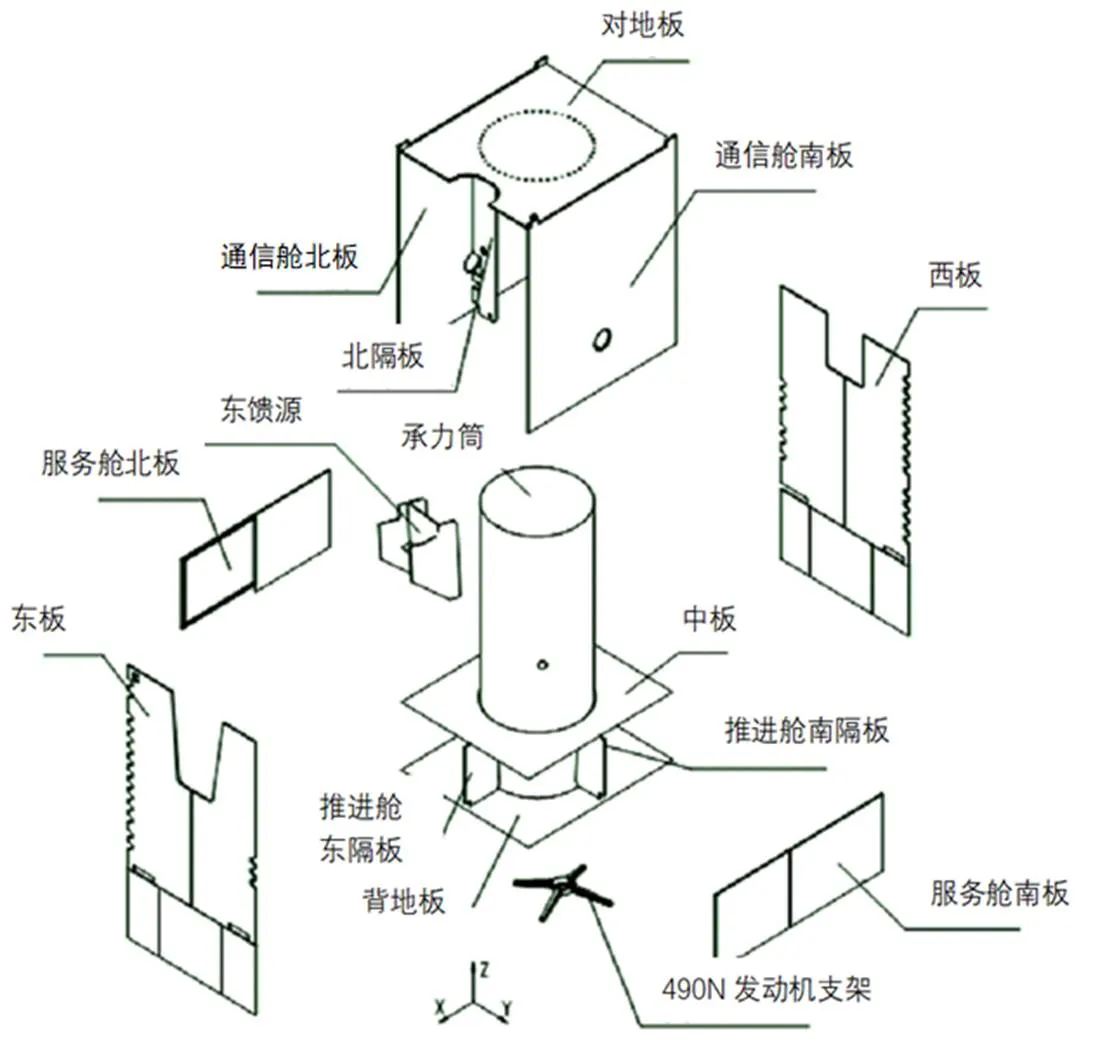
图1 卫星分解示意图

由于±太阳翼安装面、±及+对地天线安装面等关键接口具有纵向跨度大（3m以上），点位多（102数量级）、分布离散的特点，为了保证太阳翼及天线的安装精度及可靠性，在研制过程中通过对其组合加工的工艺方法，保证其形位精度满足设计要求。由于卫星在该阶段已实施管路等推进分系统项目，故对生产环境要求极为严格，需在10万级净化厂房内研制，另外加工过程不允许使用冷却液，综合以上需求，目前使用的加工设备为“三维立式加工中心（以下简称ITP）”。

ITP最早于2003年引入卫星结构部装领域。作为非接触式测量设备，可以完成大尺寸结构件高精度测量工作以及精测数据拟合工作，测量精度优于0.05mm。根据组合加工的要求，原厂在测量功能的基础上开发了组合加工功能，通过测头和加工头的转换实现功能切换，现已经广泛应用于各平台卫星关键对外接口组合加工，ITP结构如图2所示。

图2 设备实物图

2 传统加工方法及其弊端

由于ITP主要功能是三坐标高精度测量，故其三维导轨的安装精度经过激光干涉仪的严格调校与补偿，决定其移动方向是基于机床坐标系定义。而传统意义上，对于大型五轴加工机床，可以通过基准转换的方式实现卫星坐标系与机床/加工坐标系的重合，实现高精度路径控制与加工，基于UG的程序编译[1]卫星在建立整星坐标系时，要求装配工装上表面相对转台平行度≤0.03/1000mm，决定卫星的绝对姿态必然会与ITP坐标系存在一定的微小夹角，ITP设备无法实现与卫星坐标系的统一是实现自动编程的一大症结[2]。

目前由操作人员通过操作ITP手柄或面板获取实际进刀、出刀的机器坐标，进而编制加工程序，流程如图3所示，具有以下难点：

图3 组合加工流程图

a. 效率十分低下，占用主线时间长，各工序时间占比如表1所示。

表1 各工序占比分配表

b. 在程序验证时，通过旋转刀尖与设备轴保持水平后，一名操作人员操控设备验证单步程序，另一名操作人员观察刀尖位置及旋转刀盘，判断进刀和出刀位置余量是否充分，该操作过程十分繁琐，人眼很难精准判断相对位置，另外操作空间狭小，从正面和侧面观察得到的结果会存在偏差。

c. 处于卫星+侧分布的天线接口在验证时需要操作升降车高空作业，风险较大。

根据统计以上分析可以得出如下结论：

a. 在生产周期方面：由表1可以看出，整个组合加工的时间为8d，其中耗时最长的为第5项组合加工，占比50%，其次是第3项获取对刀坐标，编译程序，占比25%，此两项就占据了全部项目的75%，耗时最长，剩余项目占比时间几乎相等。在剩余的项目里其中第1项“基准坐标系测量待加工区域”、第2项“测头更换为加工头”及第6项“加工后精度测量”为固定操作，无优化空间。

b. 在程序可靠性方面：目前程序段的坐标值主要依靠操作者操作设备手动获得，可能引入误差的环节主要包括坐标记录正确性、程序段录入正确性，由于全部由人工实施，不能确保程序编制100%正确，可能引入风险。

c. 在程序验证方法方面：目前的操作方法中需要两名操作人员同时在升降车上高空作业，安全风险大，另外进刀、出刀充分性判断主要利用视觉确认，手动旋转刀盘观察刀尖是否进、出充分与操作者的手法、目测情况都有关系，存在标准不一致的难点。

d. 在加工可靠性方面：根据以往型号的加工结果，存在局部超差的情况，再二次加工，这可能与刀具材料、切削参数有关，需要进一步调研，如何提高加工稳定性、可靠性也是提高加工质量的重点方向。

本文重点从如何快速、准确获得加工坐标及规划加工路径两个方面分析。

3 加工原理

卫星以部装支架圆心为基准点，±轴上的销孔连线为基准线，指向+，对接法兰面为基准面，如图4所示，ITP机器坐标定义如图5所示，均符合右手坐标系[3]。

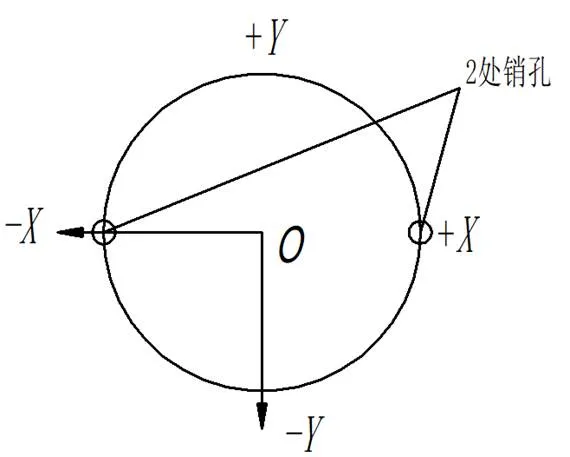
图4 卫星坐标系定义

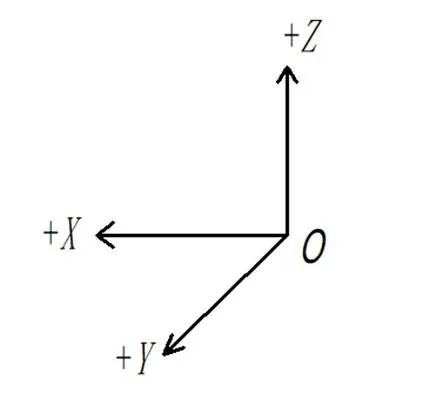
图5 机床坐标系定义（由机床面向卫星）

首先操作者通过ITP手柄或控制面板控制主轴移动，ITP属于单轴控制设备[4]，所以每次移动均为→方向或↑方向。激光发射器发射的激光投影在星体侧壁上，通过观察进入点及远离点是否处于待加工埋件的外围，确定加工余量是否充分。根据确定的进入点及远离点记录相应的坐标值，用于后续的程序编译。重复上述过程直到获得全部加工坐标。

程序示例如下：

X100 %轴移动至坐标100；

Z1600 %轴移动至坐标1600；

X40 %轴移动至坐标50；

此段程序可以解释为加工面平行于平面，从坐标（100, 1600）加工到坐标（40, 1600），即沿-向加工60mm。

根据空间直角坐标系转换的基本原理，转换坐标[5]。

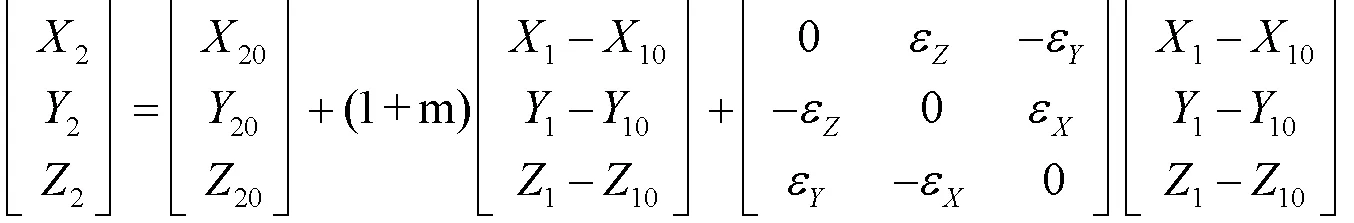
4 加工策略规划及分析

在加工过程中主要分为慢速模式（用于切削）及快速模式（用于移动），由于二者速度相差较大（大于10倍），故认为影响加工效率的主要因素集中在慢速切削模式下。以±侧天线板为例，待加工埋件具有局部集中，整体离散的特点。属于同一“图元”的埋件应划分为同一组别加工，这是由于对于每一个埋件，以横向加工为例，其加工过程为：a.→慢速靠近进入点；b.↓慢速到达加工高度；c.→慢速切削；d.↑慢速抬升至安全高度；e.快速迁移至下一点。两点在距离很近的时候，如果采用单点加工的策略，会重复a～d的过程，效率低下。所以认为可以定义“合适的距离”，以随机的点为中心向四周辐射，搜索“距离”内的点位作为分组原则，同组采取连续加工的策略[6]。该策略受“聚类算法”启发并修正适应性。聚类分析又称群分析，是研究（样品或指标）分类问题的一种统计分析方法，同时也是数据挖掘的一个重要算法。聚类[7]（Cluster）分析是由若干模式（Pattern）组成的，通常模式是一个度量（Measurement）的向量，或者是多维空间中的一个点。通过聚类算法将待加工埋件分类，用于后续加工向量长度计算，对目标函数求最优解[8]。

5 聚类分组的过程及实现

利用Python编译开发程序。其基本思路为，首先遍历孔表，利用最高点（激光跟踪仪测量获得）的标号索引（该点有利于加工程序循环次数的最小化）获得其及坐标，将坐标值作为初始化的“聚类”中心，从该中心出发向周围“搜索”距离较近的点，判断二者的距离，如果满足向不超过30mm及向不超过1000mm（此两项数据为自定义），则认为第二点属于“一号聚类”群，重复以上过程将符合条件的点归集到群中，直至有不满足条件的点位出现，将该点定义为“二号聚类群”的聚类中心，重复上述过程直至完成全部分组[9]，程序图如图6所示。程序代码略。

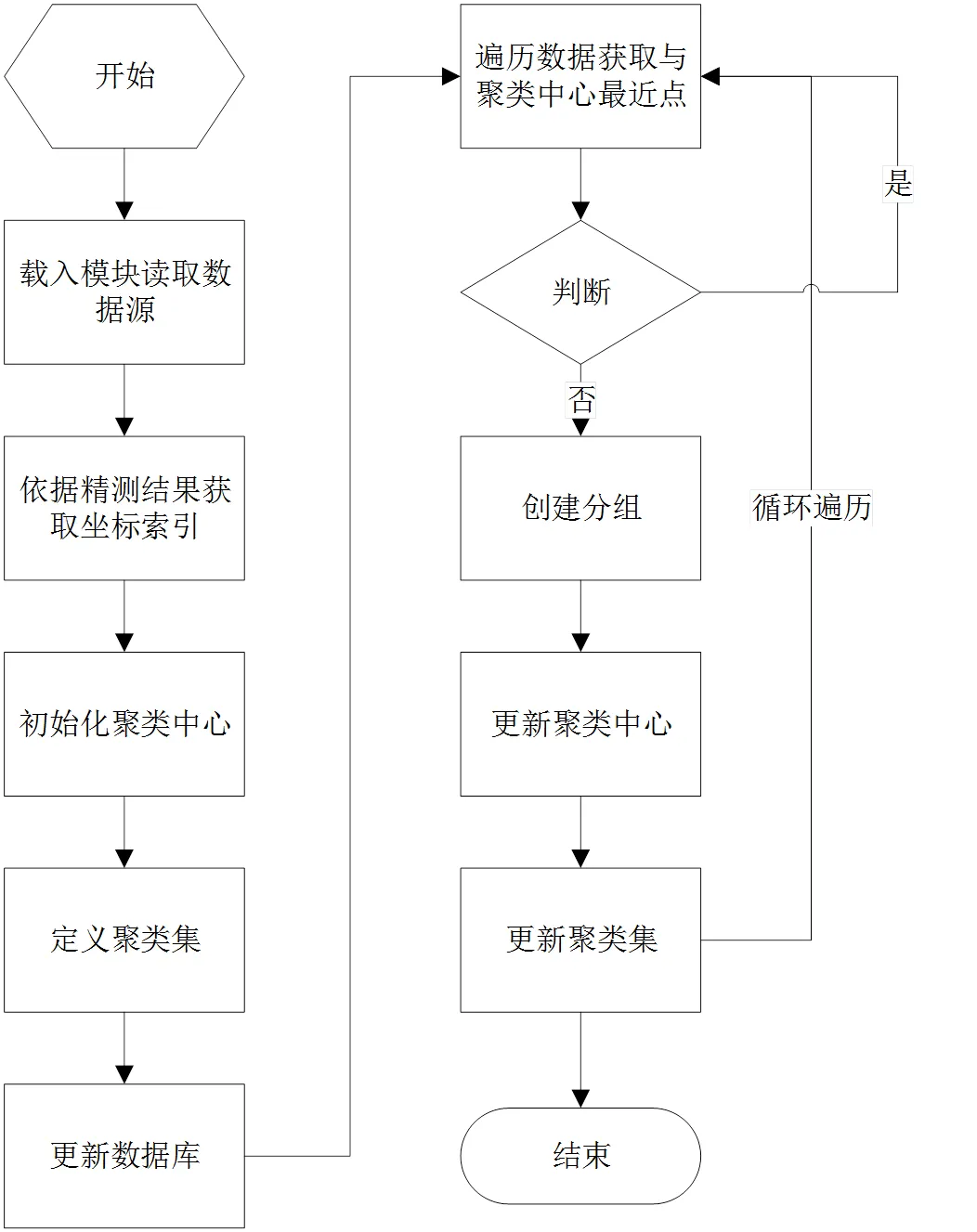
图6 程序逻辑图

6 点位及路径计算

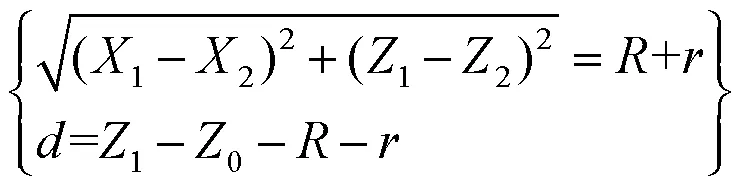
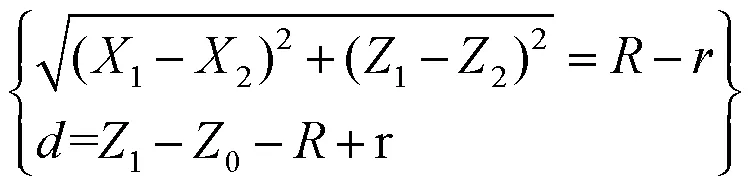
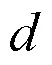
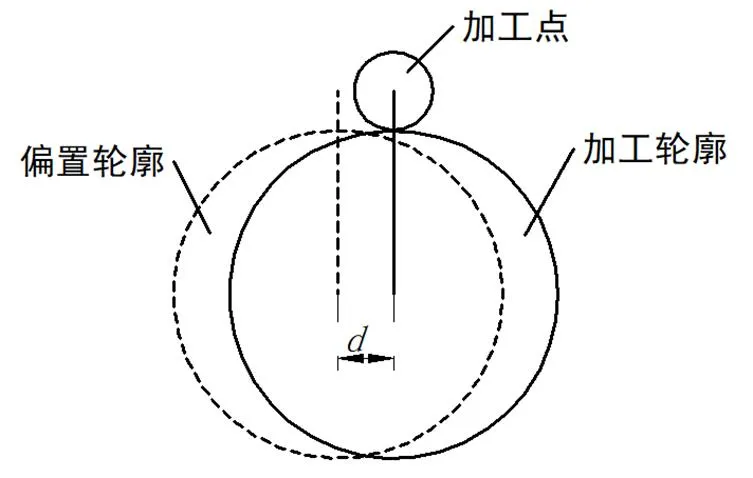
图7 路径偏置示意图

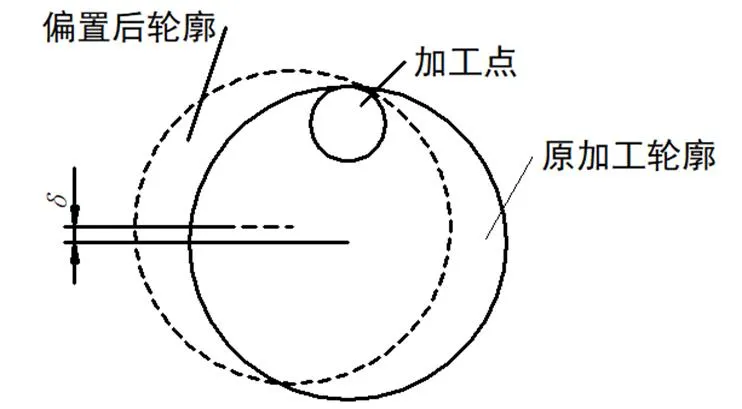
图8 路径补偿示意图

7 加工实例

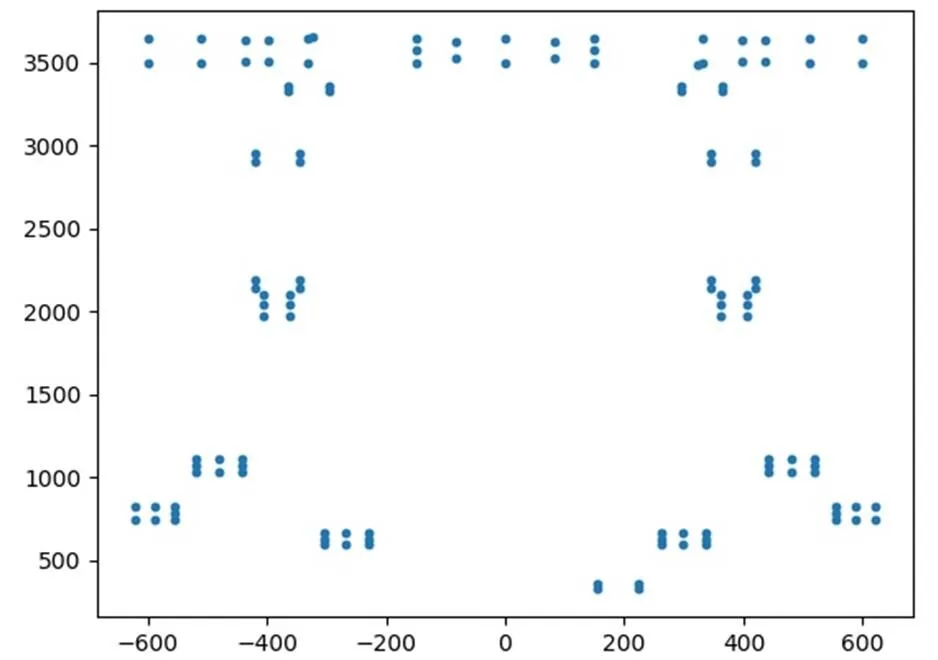
图9 分组散点图

以XX-1(03)通信卫星孔表为基础，运行上述分组程序段，可以得到分组情况（部分），将分组情况绘制散点图，如图9所示。从图中可以看出分组精确度很高，与人工判断分组情况完全一致，参数调校合理。

最终程序段如下（部分）：

X-1364.5

Y-720

Z3

G01 Z0

X-1382.5

G00 Z5

X-1534.5

Y-720

Z3

该程序完全满足加工要求，顺利完成了组合加工任务，产品各项精度指标满足要求，程序质量可靠。

利用第6章公式计算路径总长度为15070mm，加工时常预测为1150s，经过加工实际验证，路径总长度15180mm，加工时常1174s，经比对数据一致性良好，预测准确。与XX-1(02)卫星组合加工比对，其路径总长度27136mm，加工时常2102s，加工效率提高了44.1%，单个循环缩短了15.46min，完成整面加工一般需要8个循环，共缩短123.73min，效率明显提升。

8 结束语

新的加工思路与传统方法相比发生了比较大的变化，具有以下优势：

a. 采用改进的聚类算法，以加工总时间为目标，将待加工点位分组，解析了最优路径，提高了生产效率。

b. 通过坐标系转换获取全部加工点位的机器坐标值，大大减少了对刀次数，提高了生产效率，降低了高空及狭窄空间作业时常和情况，提高了安全性。

c. 程序编译全部由计算机完成，摒弃了人工输入坐标的操作，具有更高的可靠性，同时提高了生产效率。

d. 通过激光对刀装置判断加工路径及余量，仅需一名操作员在地面即可完成，解放了生产力，降低了高空作业风险，可视化更加直观，生产效率大幅提升。

下一步将根据“碰撞干涉[11]”的理论实现避障，根据几何约束条件自动完成干涉检测。另外在刀具的调平环节可以攻关新的方法，比如设计工装保证、快接接口设计等，缩短刀具调平的时间。程序验证辅助工装进行V2.0版本设计，进一步提高激光点位精度，减小安全裕度设计量，通过以上细节进一步提高ITP组合加工效率与可靠性。

1 Anil K J. Data clustering: 50 years beyond K-Means[J]. Pattern Recognition Letters, 2010, 31(8): 651～666

2 Likas A, Vlassis M, Verbeek J. The global K-means clustering algorithm[J]. Pattern Recognition, 2003, 36(2): 451～461

3 Selim S Z, Al-Sultan K S. Analysis of global K-means，an incremental heuristic for minimum sum-of-squares clustering[J]. Journal of Classification, 2005(2): 287～310

4 Bellman R, Dreyfus S. Applied dynamic programming[M]. New Jersey: Princeton University Press, 1962

5 Aloise D, Deshpande A, Hansen P, et al. NP-hardness of euclidean sum-of-squares clustering[J]. Machine Learning, 2009, 75(2): 245～248

6 Mahajan M, Nimbor P, Varadarajan K. The planar K-means problem is NP-hard[J]. Lecture Notes in Computer Science, 2009(5431): 274～285

7 Ball G, Hall D. ISODATA, a novel method of data analysis and pattern classification[M]. California: Technical rept. NTIS AD 699616. Stanford Research Institute, 1965

8 Wang Cheng, Li Jiaojiao, Bai Junqing, et al. Max-Min K-means Clustering Algorithm and Application in Post-processing of Scientific Computing[C]//Napoli: ISEM, 2011: 7～9

9 Pena J M, Lozano J A, Larranaga P. An empirical comparison of four initialization methods for the K -means algorithm[J]. Pattern Recognition Letters, 1999(20): 1027～1040

10 Lai J Z C, Tsung-Jen H. Fast global K -means clustering using cluster membership and inequality[J]. Pattern Recognition, 2010(43): 1954～1963

11 Mao J, Jain A K. A self-organizing network for hyper- ellipsoidal clustering（hec）[J]. IEEE Transactions on neural net- works, 1996(7): 16～29

A Satellite Combined Processing Technology Based on Clustering Algorithm

Zang Ziyi Cheng Ze Cai Zhaoyang

(Beijing Satellite Manufacturing Co., Ltd., Beijing 100094)

Based on the research background of the combined processing field of communication satellite solar wing and antenna interface, this paper analyzes the shortcomings of current processing methods. Firstly, based on the analysis of graphic elements, the machining process is enhanced and simulated, and the transition matrix between the machining coordinate system and the satellite coordinate system is constructed using the principle of space coordinate system conversion to realize the overall output of the machining strategy. In terms of path planning, this paper proposes “a processing path planning scheme based on clustering algorithm”, which achieves the optimal processing path planning through a series of processes such as random initialization of cluster centers, “distance” judgment, automatic classification, and vector length cumulative summation. In this method, both the processing path and the migration path are planned by the computer, which reduces manual intervention and improves the efficiency and accuracy of prediction. It laid a theoretical foundation for the subsequent realization of intelligence and automation. This method has been verified on the satellite model, and the processing accuracy has reached the domestic advanced level.

communication satellite；image element analysis；clustering algorithm；path planning

TH181

A

臧梓轶（1989），工程师，机械工程及自动化专业；研究方向：航天器制造。

2021-07-20