双机抬吊法吊装某井筒的过程静力学分析
金忠见
(中国核工业二三建设有限公司,北京 100000)
0 引言
从全球核电产业发展来看,各个国家的大部分核电站的在堆贮存水池容量已经超负荷,乏燃料的后处理已经成为亟待解决的问题之一[1]。通常情况下,当乏燃料在堆水池已满或接近满容,而后处理厂或放射性废液处理库的建设相对滞后时,均会采用乏燃料中间贮存的办法。近年来,我国加大了对于核设施退役预算的投入,国内第一个离堆的乏燃料干式贮存设施是由秦山第三核电有限公司建设,该技术源于加拿大原子能公司的气冷贮存模块[2]。常规的干法贮存是指将高放废液玻璃固化后贮存在容器暂存库中。对于高放射性固化体贮存井的安装,其精度要求很高,井筒必须插入顶板贯穿件内,使井筒与贯穿件部分重叠,形成一个定向支座来平衡侧向力。如果井筒发生较大变形,其后续安装工作均会受到影响。对零部件吊装过程进行静力学仿真分析可以为实际吊装过程提供参考。文献[3]对于某特种方舱骨架在运输、吊装、天线起竖等工况下进行静力学分析,对部分构件的设计提出了合理建议。杨建福[4]基于ANSYS软件对动车组水箱吊装结构强度分析,确定了吊装结构中应力较大的部位,发现螺栓孔等应力较大部位的接触应力均小于材料的屈服强度。梁全章[5]对某工程实例进行有限元建模,通过ANSYS软件对钢-混组合梁斜拉桥主梁整体吊装进行受力分析,结果表明梁处于吊装过程中的最差工况时,梁的受力仍然满足要求。
本论述通过ANSYSWorkbench静力学分析模块对高放射性固化体贮存井吊装过程进行有限元分析,并对抱箍的安装位置进行调整,以确定抱箍的最优安装位置,为井筒吊装过程的可行性与安全性提供依据。
1 三维有限元模型建立
高放射性固化体贮存井主要由两百多个井筒单元构成。如图1(a)所示为贮存井的井筒单元,井筒单元主要由贯穿件、定位钢板、井筒和贮存井底板构成。玻璃固化体贮存于每个井筒单元内以保证安全。这种嵌套式的结构对安装有严格的要求,井筒可视为细长件,在吊装过程中容易出现变形,同时禁用铁件及其它锐利工具碰触井筒。因此井筒吊装采用双机抬吊法,如图1(b)所示,起吊端使用塔吊与井筒预留耳洞通过扁担梁相连,溜尾端使用汽车吊通过抱箍与井筒相连进行吊运。

图1 (a)井筒单元;(b)双机抬吊法吊装井筒
为了验证井筒在吊装过程中的变形大小,现对井筒吊装过程中的三种运动状态进行静力学仿真,同时研究改变抱箍位置对变形的影响,分析井筒应力分布。图2显示了井筒的三维模型图及相关参数,井筒总长L为10 775 mm,其外径D为490 mm,井筒壁厚t为5 mm,井筒的右端开设有四个均匀的圆孔用于塔吊吊装,其圆孔直径为80 mm。井筒的左端外表面安装有用于汽车吊的抱箍,抱箍安装在距离井筒端面长度为d的位置,井筒吊装过程中改变d的值来分析井筒的应力与变形状况,使吊装过程中的位移变形最小。状态1指的是起吊刚开始汽车吊与塔吊将井筒水平吊起的状态,状态2为塔吊升高后井筒与地面成45°角时的状态,状态3为汽车吊撤离后井筒被竖直吊起的状态。上述三种状态均为吊装过程中井筒保持动态受力平衡的过程,不考虑吊装过程中井筒随时间的运动状态,因此计算过程为稳态。
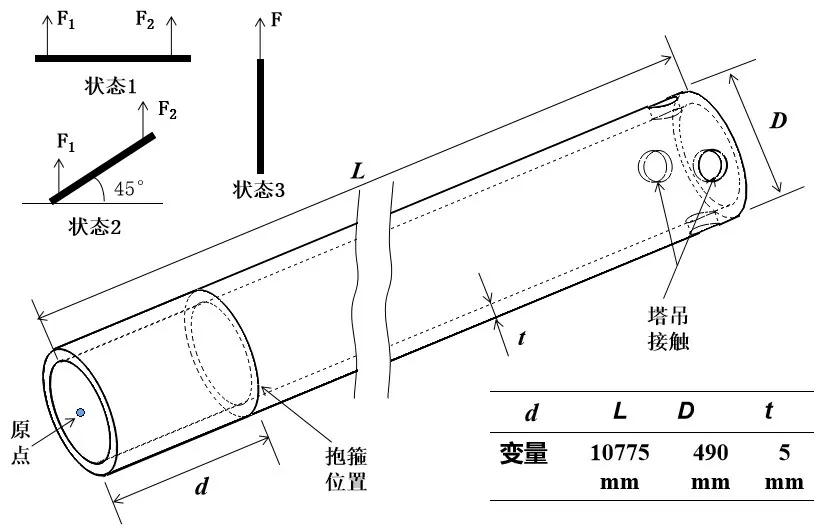
图2 井筒三位模型图及相关参数
井筒的材料为316Ti不锈钢,其物性参数见表1所列。

表1 材料特性参数
2 网格划分及添加载荷
根据上述分析在Solidworks中建立三维模型,导入Ansys workbench的静力学分析模块进行材料、网格、边界调节及求解的相关设置。网格划分结果如图3所示,对局部带有吊装孔的位置进行加密处理,对不同状态的三位井筒模型,其节点单元为11万左右。需要说明的是,有限元法处理静力学问题时并非网格数越多越好,对于本模型而言,为了避免出现应力奇异,网格节点控制在11万左右,未出现应力奇异,满足有限元计算要求。

图3 井筒有限元网格划分
有限元模型约束条件及假设:假设井筒在三个状态受力分析时均保持动态平衡,不考虑井筒随着时间的运动,为稳态计算。井筒自身重力视为均布载荷分布于井筒外表面,其值q=12 310 N,不考虑其它外部载荷。动态平衡后汽车吊与塔吊对井筒的约束视为铰支,忽略井筒材料的不均匀性。
3 静力学仿真结果分析
针对上述三维模型及其运动状态进行有限元计算,结果分析如下,图4为d=200 mm时井筒处于状态1的动态平衡时,井筒的最大位移云图,为方便观察,变形位移量按照130倍放大显示。从图4可以看出,最大位移发生在井筒的正中间处,大小为4.07 mm,井筒两边的位移基本为0。图5为d=200 mm时井筒处于状态1的动态平衡时,井筒的等效应力云图,可以发现应力的最大值分布在井筒右侧的小孔位置处,最大值为9.772 6 MPa,同时井筒中间的应力也较大。

图4 d=200mm、井筒处于状态1时位移分布

图5 d=200mm、井筒处于状态1时等效应力分布
为研究抱箍安装距离d对井筒最大位移变形及最大等效应力的影响,当d值取200 mm、400 mm、600 mm、800 mm和1 000 mm时,对于状态1和状态2而言,井筒的最大位移随d的变化过程如图6(a)所示,发现随着距离d的增加,井筒所受的最大位移值在减小,井筒处于状态1时的最大位移高于状态2,其最大位移发生在d=200 mm且井筒处于状态1时,其值为4.07 mm。通过有限元计算得知,状态3时井筒最大位移为0.2 mm,因此井筒在状态1时的位移变形最明显。井筒的最大应力随d的变化过程如图6(b)所示,可以发现,状态2时井筒所承受的最大应力大于状态1,最大应力出现在d=200 mm且井筒处于状态2时,其值为19.07 MPa,通过有限元计算得知,状态3时井筒最大应力为20.93 MPa,因此井筒在状态3时所承受的最大应力值高于状态1和状态2,同时最大应力的位置出现在用于起吊的小孔位置。根据上述分析可知,井筒采用双机抬吊法吊装过程中受到的等效应力远小于屈服应力,同时吊装过程中井筒的最大位移变形为4.5 mm,不会对井筒的安装精度造成影响,因此采用双机抬吊法吊装的方法不会对井筒造成变形或应力失效,其方法可行性程度高。
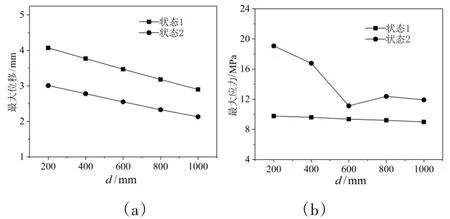
图6 井筒最大位移与最大应力随d的变化
图7为抱箍的约束反力随距离d的变化,井筒处于状态2时抱箍所承受的约束反力均高于状态1,同时随着抱箍安装距离d的增大,其所承受的约束反力在逐渐增大,因此在采用双机抬吊法吊装井筒时须确保受力平衡;对比图6(b)中状态2时最大应力随d的变化,当d=600 mm时,最大应力值最小,因此抱箍安装的距离d的优选值为600 mm。
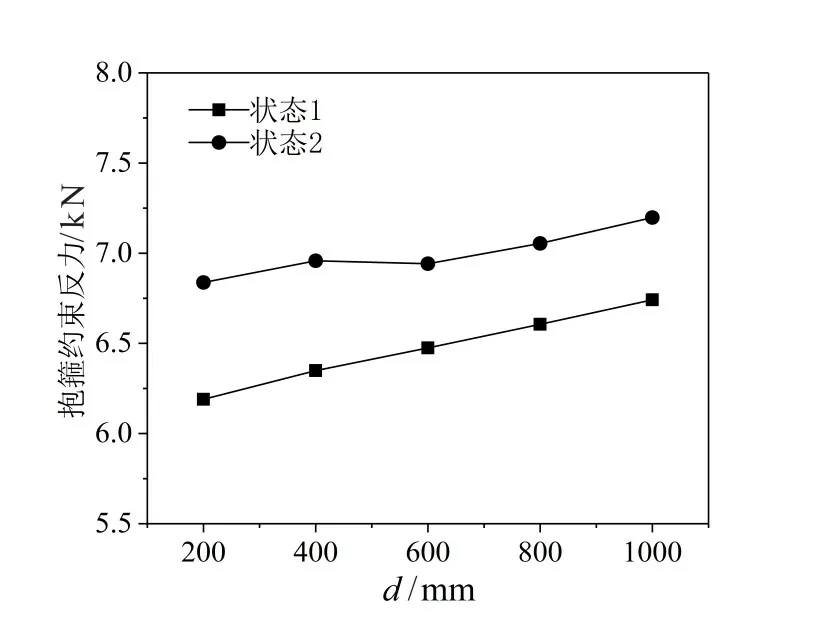
图7 抱箍的约束反力随d的变化
4 结论
本论述对与双机抬吊法吊装某井筒的过程进行了静力学仿真分析,通过对吊装过程中的三个动态平衡状态进行有限元计算,得到了以下结论:
(1)采用双机抬吊法吊装井筒时,当井筒与地面平行时,井筒的位移变形最大,最大位移发生在井筒的正中间;当井筒与地面垂直时,井筒承受的最大等效应力值最大,且位于井筒端部用于起吊的两个圆孔上。
(2)当井筒与地面的夹角为45°时,抱箍与井筒端面的距离优选600 mm,此时井筒所受的最大应力最小。
(3)采用双机抬吊法吊装井筒时,井筒承受的应力与变形均在合理范围之内,采用此方法吊装井筒的可行性较高。

