基于回算机制的GPS/INS时间延迟处理方法

汪 菁,孙立海,邹瑜光

(神州五行航天科技有限公司，辽宁 大连 116020)

低成本制导炸弹作为一种精确对地攻击弹药，因其具有成本低、结构简单、精度高、适合大量使用等特点，受到世界各国青睐[1-2]。为降低成本，低成本制导炸弹中常采用微机电系统[3](Micro Electromechanical Systems，MEMS)作为惯性测量器件进行惯性导航(Inertial Navigation System,INS)计算。但由于MEMS器件存在零偏漂移较大、零偏重复性差[4]等缺点，单独使用会严重影响导航定位精度，因此低成本制导炸弹中常采用GPS接收机输出定位和定速信息，通过卡尔曼滤波算法，对导航结果进行修正，即松耦合形式的GPS/INS组合导航。

采用卡尔曼滤波算法对来自不同器件的相关信息进行融合时，关键在于要保证融合的数据在时间点上的一致性[5-6]。由于GPS与INS工作频率不同，且INS由于自身特性导致数据更新频率也不是恒定值，因此采集数据不可能拥有同一时标。GPS接收机的输出信息一般是经过接收机内部滤波算法处理后的结果，且由于数据转换和串口传输速度等因素的影响，GPS与INS在进行数据融合时存在时间不同步的现象，往往只是同步到数据输出时刻，而无法同步到GPS信息更新时刻，这将导致最终定位精度下降，使导航整体性能变差[7]。

为保证组合导航过程中数据融合的时间同步，国内外众多学者提出了不同的处理方法，大体上可以归结为硬件实现、软件实现或软硬件相结合的方法[8-10]。硬件上可采用秒脉冲(1 Pulse Per Second，1PPS)的方法控制采样电路，或利用高精度计数器和INS脉冲实现GPS与INS的时间同步，但硬件实现方法通常需要增加额外的硬件，成本较高，且不适用于大多数已封装好的INS测量单元，因此该方法的适用性较差。软件上常结合卡尔曼滤波算法，在状态变量中添加时间延时项[11-12]，利用插值、外推等算法对GPS输出的速度、位置信息进行补偿，采用补偿后的信息进行数据融合，估计出时间延迟量[13]。这类方法由于增加了状态变量个数，使运算量加大，导致计算时间延长，加大了处理器的负担，对于低成本弹机处理器要求较高，容易造成输出延迟。软硬件相结合的方法则是利用多项式拟合[14-15]来描述GPS输出，利用存储的GPS信息和延迟时间计算多项式拟合系数，继而获得信息融合时刻真实的GPS输出，从而与对应时刻的INS信息进行数据融合。理论上多项式次数越高，拟合精度越高，延迟补偿效果越好，但同时也需要存储更多的数据点。通常可根据载体运动的剧烈程度来选择不同的拟合次数，但这在一定程度上增加了程序的复杂度。现有的软件实现方法和软硬件相结合的方法均不允许GPS数据存在丢失的情况，尤其是在载体运动状态变化剧烈的时候，否则会引入较大的误差，这对低成本弹机的性能提出了严格的要求。

不论利用何种方法，均不能完全消除时间延迟所带来的影响。过度追求精密仪器和复杂的软件补偿方法，不仅对提高定位精度影响甚微，还会影响成本造价。因此从实际角度出发，相对简易的补偿方法更适用于低成本制导炸弹。本文在采用软硬件相结合的方法的基础上，提出一种回算机制，完成组合导航在GPS信息更新时刻的融合，在GPS数据输出时刻输出，减小时间不同步对系统定位精度的影响。同时，不额外添加卡尔曼滤波状态变量，避免较大的计算量，在GPS信号丢失时仍可使用，不增加程序复杂度，适用性强，可满足低成本制导炸弹及中低精度导航需求。考虑到低成本处理器的能力限制，本文同时提出一种配合回算机制进行的工程计算优化算法，在回算过程中取消卡尔曼滤波计算的时间更新操作，节约计算时间，缓解处理器在回算过程中的计算压力，同时对定位精度不产生明显影响，具有较强的工程实用性。

1 回算机制

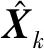
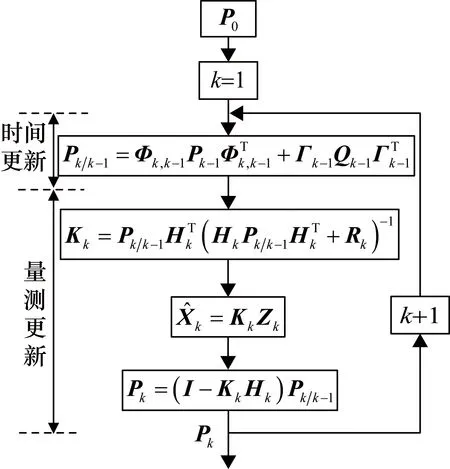
图1 间接法对应的卡尔曼滤波流程图

(1)

(2)

(3)

(4)

Pk=(I-KkHk)Pk/k-1

(5)

在GPS/INS组合导航系统中，GPS信息尚未到来时，系统根据惯性器件采集的信息进行惯性导航计算，同时根据系统性能等参数完成时间更新操作；当GPS信息更新后，根据获取的GPS量测信息对惯性导航结果进行修正，完成量测更新操作。由于GPS一帧数据较长，且串口传输速率有限，因此GPS数据并不是在接收瞬间完成输出的，而是存在一定的时间延迟。根据GPS接收机设备的不同及处理器性能差异，通常一帧GPS数据时延为15～95 ms[17]。若GPS时延15 ms，载机挂弹以300 m/s速度飞行，则在进行量测更新操作时，GPS位置误差在原有基础上又增加4.5 m。持续的时延会对最终定位产生不利影响，因此需要对GPS时延进行补偿。

通过对比可知，软硬件相结合处理GPS时延的方法更适用于低成本制导炸弹，但现有的方法不允许GPS数据出现丢失，否则可能造成存储数据量过大，导致存储器压力激增或插值拟合数据异常，从而影响导航计算结果。针对这种情况，结合卡尔曼滤波和GPS/INS组合导航的特点，本文提出一种回算机制，既可完成对GPS时延的补偿，又适用于GPS数据短暂丢失的异常情况。

具体方法如下：依次调取MEMS模块和GPS模块，并采集数据。利用硬件对采集到的MEMS数据标记时间戳，GPS接收机在接收到新数据时，会提供1PPS，触发中断，此时标记GPS接收数据时间戳t1，并根据校验位判断是否已接收到完整的GPS数据。若未收到，则采样下一时刻的MEMS数据；若已收到，则标记GPS输出数据时间戳t2。

正常情况下的回算机制示意如图2所示。未发现接收数据时间戳t1时，弹机利用MEMS数据完成惯性导航计算，同时利用式(2)完成时间更新。当发现t1后，正常完成惯性导航与时间更新计算，同时预设存储器存储当前导航结果和MEMS数据，直至t2到来，在此之前，按MEMS采样频率正常输出惯性导航的计算结果。在t2时刻，GPS完成数据接收并输出，此时调取存储器中存储的t1时刻MEMS数据，利用式(3)～式(5)进行量测更新，与GPS数据完成数据融合。在此基础上依次调取存储器中(t1,t2]区间内存储的MEMS数据，完成惯性导航计算，输出t2时刻(即当前时刻)导航结果。至此完成一轮完整的回算操作，清空存储器后，采样下一时刻的MEMS数据，进行惯性导航计算，并等待下一秒GPS接收数据时间戳的到来。

图2 正常情况下回算机制示意图

若GPS接收数据过程中出现异常导致数据丢失，或接收时间过长，则存储器中存储数据将过量。考虑到固定的GPS接收机，正常情况下GPS时延在某一范围内小幅波动，因此可根据前期测试得到GPS时延的上限值，并根据GPS时延上限时长与MEMS采用周期设置存储器最大存储长度。如图3所示，假设预设的存储器最大存储长度为6，则在t1时刻后第7拍存储时会出现存储器溢出的现象，此时清空存储器，放弃GPS更新操作，组合导航自动退化为惯性导航，直至下一秒GPS接收数据时间戳的到来，再次进入回算机制。预设存储器长度可以避免存储器存储过多的数据，减小对系统存储空间的压力，同时可以避免因某一次接收数据异常而对后续流程产生不利影响。若放弃某一次回算，则组合导航在该时刻自动退化为惯性导航，不影响输出，短时间内不影响导航精度。

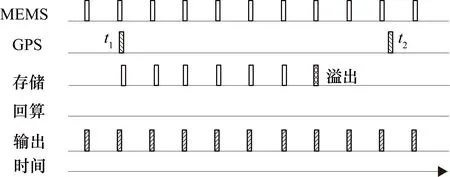
图3 异常情况下回算机制示意图

采用上述回算机制处理GPS时延，无须增添状态变量，不增加卡尔曼滤波算法的计算量。该回算机制仅需存储一步惯性导航结果、有限步MEMS数据，可避免GPS数据异常对存储空间和计算精度带来的不利影响。除了判断时延长度是否超过预设值外，程序执行上仅需调用原有程序模块，无新增处理环节，不增加程序的复杂度，在工程实践中具有较好的实用性。

2 工程实践中的计算优化

为不干扰正常导航计算与输出，采用回算机制处理GPS时延时需保证处理效率，并及时输出。但在实际操作中常出现回算过程占用较长的处理时间，导致后续控制延迟明显，继而影响了下一时刻的MEMS数据采样，造成数据整体延迟。在现有低成本处理器的能力内，考虑采取一定的计算优化，以达到节约回算时间、避免数据延迟的目的。

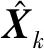
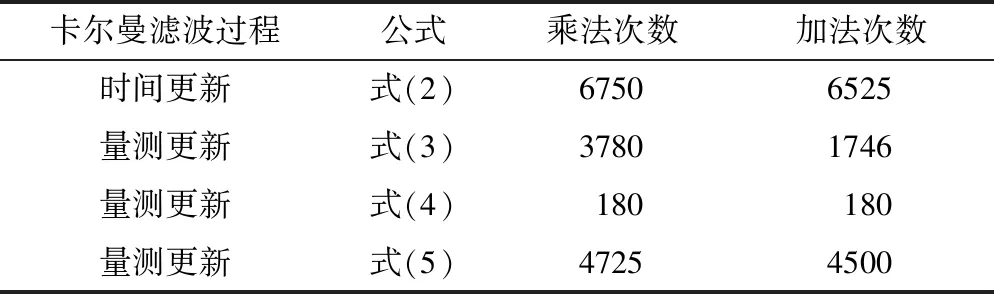
表1 卡尔曼滤波过程所需乘法与加法次数

由于量测更新阶段的计算更新频率低，且必不可少，因此考虑从更新频率相对较高的时间更新计算上进行优化。由式(2)可知，在时间更新环节中，一步预测均方误差阵Pk/k-1依照估计均方误差阵Pk、一步转移阵Φk,k-1、系统噪声阵Qk-1等参数调整。对于固定的MEMS器件，系统噪声特性基本稳定，不存在大范围的波动。而一步转移阵计算公式如式(6)所示(其中系统矩阵F参考文献[15]中式(14.63))，由于采样时间Δt通常较小，在短时间内Φk,k-1调整量较小。

Φk,k-1≈I+F·Δt+F·(Δt)2/2

(6)

由此可看出，一步预测均方误差阵Pk/k-1在短时间内与估计均方误差阵Pk差别较小。考虑到回算之前，已计算过t1至t2时间段内的一步预测均方误差阵Pk/k-1，若在回算中再次计算Pk/k-1，不仅数值上前后差别不大，且会占用较多计算时间。因此从实际工程角度出发，可取消回算过程中时间更新计算环节。该项计算优化算法在理论仿真和实际应用中均得到验证，可节约计算时间，不影响定位精度，适用于低成本弹机处理器，工程应用效果较好。

3 算法验证及分析

3.1 回算机制验证

结合某型低成本制导炸弹靶试，验证在实际应用中回算机制对GPS时延的补偿效果，其中MEMS和GPS基本性能指标如表2所示。

表2 某型低成本制导炸弹导航仪器性能指标

试验条件：载机挂载制导炸弹以速度为Ma=0.6、海拔高度为5500 m飞行，绕靶场平稳挂飞后投放。初始位置和速度均由GPS提供，初始姿态角由载机提供，姿态角误差±2°。

MEMS器件采样频率200 Hz，GPS输出频率1 Hz。经前期测试，GPS时延不超过30 ms，因此回算机制中预设存储器长度为6。

状态估计均方误差阵初值P0、系统噪声阵初值Q0、量测噪声阵初值R0设置如下：

P0=diag{2°,2°,2°,0.1 m/s,0.1 m/s,0.1 m/s,6.298×10-5°,8.062×10-5°,15 m,20×10-3g,20×10-3g,20×10-3g,30°/h,30°/h,30°/h}2

Q0=diag{30°/h,30°/h,30°/h,20×10-3g,20×10-3g,20×10-3g,0,0,0,20×10-3g,20×10-3g,20×10-3g,30°/h,30°/h,30°/h}2

R0=diag{6.298×10-5°,8.062×10-5°,15 m,0.1 m/s,0.1 m/s,0.1 m/s}2

利用弹机硬件记录GPS接收和输出时间戳，并遥测下发。根据遥测数据记录，靶试飞行期间GPS数据时延如图4所示，其中纵坐标为每秒接收到的GPS输出时间戳与接收时间戳的差值。实测结果表明在制导炸弹飞行期间，GPS时延基本在15～25 ms区间内，与前期测试相符。

图4 飞行期间GPS时延

按遥测数据进行再现，对比使用回算机制及未使用回算机制时导航定位与GPS间误差，具体结果如图5～图8所示，其中图5～图7依次为有无回算机制下定位误差在导航系各方向(北向、东向、天向)上的对比，图8为空间定位误差对比，蓝色曲线表示有回算机制时导航与GPS间的定位误差曲线，橙色表示无回算机制时的定位误差。由对比结果可知，除高程定位差别较小(平稳挂飞，高程变化较小)外，使用回算机制时导航与GPS间定位误差总体上小于未使用回算机制时的定位误差。该误差会影响靶试最终精度，使用回算机制时最终定位精度约为3.83 m，而未使用回算机制时最终定位精度约为12.15 m。

图5 有无回算机制对北向定位误差的影响

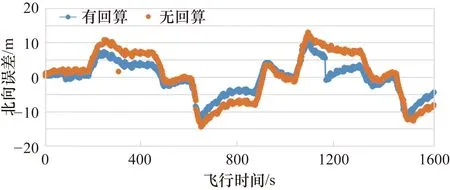
图6 有无回算机制对东向定位误差的影响

图7 有无回算机制对高程定位误差的影响

图8 有无回算机制对空间定位误差的影响

3.2 计算优化验证

在相同的条件下对比使用计算优化算法前后的计算效率及其对导航定位精度的影响。

以台式计算机(Intel®CoreTMi5-3470，CPU 3.20 GHz，12 GB RAM，64位操作系统)为例，在C语言运行环境下，运行A、B两套含回算机制的导航仿真程序，其中A程序未采用计算优化，B程序采用计算优化。人为设定GPS时延15 ms，A程序完成一次回算过程耗时约0.1 ms，B程序完成一次回算过程耗时约0.047 ms，采用优化算法在单次回算过程中可节省约一半的计算时间。使用低成本弹载计算机运行A、B两套程序，A程序在回算过程中运行时间超过MEMS采样周期，导致后续控制延迟明显，而B程序可保证回算过程运行时间小于MEMS采样周期，不增加延迟，实际应用效果较好。

利用靶试遥测数据，验证本文所提出的计算优化对导航定位精度的影响。图9、图10为采用计算优化前后的定位误差对比及两者间偏差结果，由图可知，取消回算过程中的Pk/k-1时间更新对导航定位精度无明显影响，计算优化前后定位偏差小于0.15 m，对于短时间内的低成本组合导航来说，该量级误差可忽略。

图9 有无计算优化对定位误差的影响

图10 有无计算优化定位偏差

4 结束语

针对组合导航算法中数据融合的时间不同步现象，本文提出了一种适用于低成本弹机处理器的回算机制，对GPS输出时延进行补偿，可适用于GPS数据丢失或异常等情况，且不增加程序复杂度，不给系统存储空间带来过大的压力。同时提出一种工程实践中的计算优化，取消回算过程中Pk/k-1的时间更新操作，不影响导航定位精度，节省计算时间，对于低成本制导炸弹具有较好的工程实用价值。