变水头装置液位开关的不确定度评定方法

沈昱明，陆 峰

(上海理工大学 光电信息与计算机工程学院，上海 200093)

在变水头液体流量标准装置(以下简称“变水头装置”)中，需要采用液位开关(或称液位计、液位传感器等)来检测容器(水柜)中液位高度，以确定流过被校流量计的水的标准体积。显然，液位开关的不确定度将对计量结果的不确定度产生重要影响[1]。但目前尚未发布关于变水头装置的检定规程，并未对液位开关的不确定度评定进行官方规定，故笔者希望通过研究液位开关相关特性，讨论其不确定度的评定方法，为相关装置的检定规程提供理论依据。

在JJG 164—2000[2]中给出了液位计(电子衡器)动态响应不确定度的评定方法，即：“将两个液位传感器固定在同一个水平位置上，使其由上升的液体同时触发，或使两个液位传感器同时向下移动，碰到水面分别记录触发时间t1、t2”，则液位传感器的动态响应不确定度为

(1)

式中,tmin为最少测量时间。

张金祖等[3]针对相关变水头动态容积法水流量标准装置分析了电容式液位传感器动态响应不确定度的公式(式(1))的运用。朱碧玉等[4]根据变水头流量标准装置的校准方法,分析了装置的不确定度分量,并运用式(1)对一实际变水头装置进行了测试，测试结果显示，被检液位开关的最大不确定度为0.015%。

笔者认为，采用JJG 164—2000来评定变水头装置液位开关的不确定度并不十分恰当。首先，很难采用有效的工装夹具，使“两个液位传感器固定在同一个水平位置上”，也很难衡量两个液位传感器是否处在“同一个水平位置上”；其次，从电容式液位开关工作原理和结构上看，只有当液体浸没到液位开关一定距离(电容值达到一定值)后，才能通过放大电路输出电平或PNP、NPN集电极导通信号。因此，即使两个传感器处在“同一个水平位置上”也没有意义。另一方面，即使不处在一个水平位置上的2个液位开关，总是可以通过调节灵敏开关，使2个液位开关的响应完全一致。其次，采用式(1)对液位开关的动态响应的不确定度进行评定的方法也值得商榷。

为此，本文选择了流量标准装置中常用的外侧测量的电容式和导纳式两种液位开关[5]进行研究，通过建立两者动态响应理论模型，分析并讨论两者相同点与差异，并因为模型的动态响应特性呈近似单调线性特征，设计开展了相关动态响应实验，以步进电机为载体，利用测距重复性进行不确定度评定；由此论证了其不确定度的评定方法的可行性和准确性，为后续理论研究提供了依据。

1 液位开关动态响应理论模型

1.1 电容式液位开关

所选用的其中一种被测液位开关是从德国进口的电容式液位开关，其结构和工作原理如图1所示。

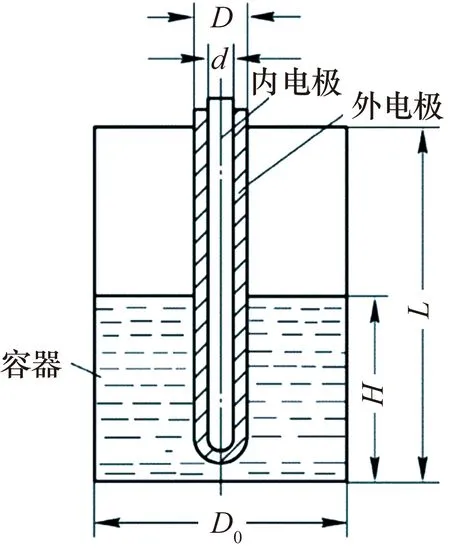
图1 电容式液位开关的结构和工作原理

设被测液体的介电常数为ε1，绝缘套管和空气组成的介电常数为ε0，液面高度为H，电容器总高度为L，内电极外径为d，绝缘套外径为D，容器内径为D0。

未注入液体时的初始电容为

(2)

当液面上升到H时，总的电容为

(3)

因为ε1≥ε0,D0/d≥D/d，故

(4)

由式(4)可见，电容增量ΔC与被测液位的高度H呈线性关系。另外，为了减小粘附层(也称“挂料”)影响，实验液位开关将内电极直径做得很细。

1.2 导纳式液位开关

所选用的另一种被测液位开关是国产的射频导纳式液位开关，其工作原理是传感器检测到水面时的导纳的变化，其结构和工作原理如图2所示。

图2 导纳式液位开关的结构和工作原理

导纳式液位开关是基于电容式液位开关研发的，其通过测量传感电极的复数阻抗变化排除了原本挂料对于测量的影响。由于挂料的横截面积较小，挂料的等效电阻较大，装置挂料等效电路如图3所示。

图3 装置挂料等效电路图

在理想情况下，由挂料的等效电路可得到带有挂料的传感器的等效电路，如图4所示。

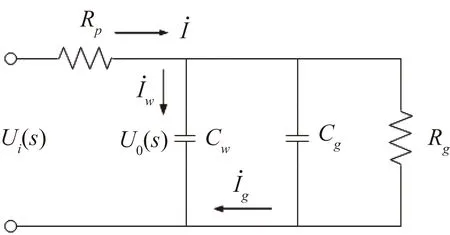
图4 带有挂料的传感器的等效电路图

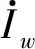
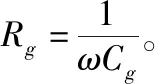
(5)

(6)

图5 物位电流与挂料电流的相位关系

2 液位开关的动态响应

考虑电容器的粘附层影响[8-9](但忽略电感作用)，电容液位开关(传感器)的等效电路如图4所示。

考虑到Rg>>Rp[10-11]，则可以导出电容液位开关的微分方程为

(7)

其传递函数为

(8)

显然，简化后的电容液位开关是一个一阶系统，其时间常数为

τ=(Cw+Cg)Rp

(9)

(10)

从式(10)可以看出，随着ω增大，粘附层影响将减弱。由此得到结论：导纳式液位开关可以有效消除粘附层影响，但时间常数却略大于电容式液位开关[12]。

3 实验方法

考虑到实际情况和研究的通用性，本文不能针对特定变水头流量标准装置设计实验，为了尽可能还原变水头流量标准装置的实际工况，将被测液位开关倾斜固定在一直线导轨滑台上，滑台通过丝杆由步进电机带动上下运动，等效于标准装置内部液面的下降与上升状态；而整个实验装置固定在一盛满水的容器(等效标准装置)上方，如图6所示。

图6 实验装置组成

3.1 步进电机重复性测试

考虑到滑台对测试结果的影响，在对液位开关动态响应进行测试前，对滑台重复性进行了测试。测试方法是当步进电机带动液位开关经过2个固定挡板时，通过光电传感器记录步进电机经过的距离，以测试步进电机的一致性。测试结果如表1所示。

表1 测试装置重复性测试

由于流量标准装置结构存在差异性，横截面积大小不一，本文选取常用的检定工作中使用的流量值[13]20 m3/h和40 m3/h近似对应的0.2 m/min和0.4 m/min两个速度进行测试。

挡板之间的距离约39 mm，考虑到回程误差，采取电机正、反转对比实验。并根据式(11)得到装置的单次测量实验标准差s(μm)。

(11)

则装置的相对不确定度为

(12)

式中，Hmin为变水头装置中2个液位开关的最短距离。

本文设Hmin为1 m。从测试结果可以看到，测试装置的最大相对不确定度为0.0018%。

3.2 液位开关动态响应测试

实验时，先下降液位开关，使其浸没到水面以下一定距离，并在程序内部初始化设为零位位置。然后设定步进电机转速，启动步进电机，丝杆以设定速度带动液位开关向上运动，模拟变水头装置水柜中的液面向下移动。当水面经过液位开关作用点时，发出TTL电平信号。测试系统中，装置采用中断方式，记录液位计从零位到离开水面时刻的距离和时间。重复实施n次实验，实验数据反映了被测液位开关的随机动态响应的不确定度。

分别对电容和导纳两种液位开关进行了实验。其中，电容液位开关共实施了6个电机上升速度(相对水面下降)；导纳液位开关共实施了4个电机上升速度，以观察变水头流量对液位开关动态响应的影响。每个速度下重复进行10次实验，计算其标准不确定度。为防止容器液面内部的波动对测试结果的影响，将测试系统装置静置一段时间后，对电容液位开关在3个速度下再次进行了实验，以检验液位开关的复现性。相对标准差计算公式同式(12)，将实验结果处理归总，测试结果如图7所示。

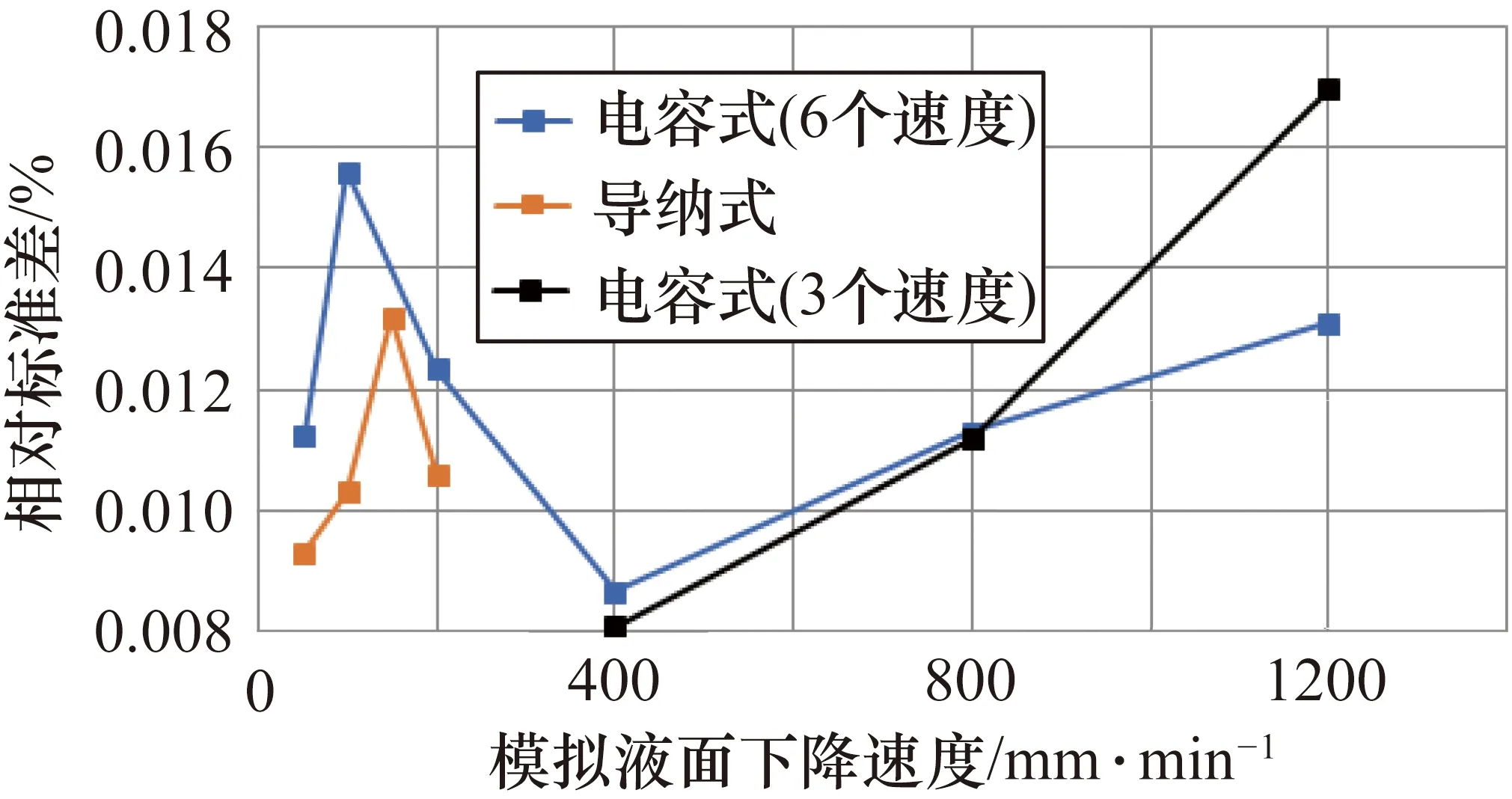
图7 两种液位开关动态响应测试结果

从图7可以看出，在相同测试条件下，电容式液位开关的标准差与导纳式液位开关基本相同；随着速度增加，标准差也有增加的趋势，说明变水头流量标准装置工作状态下的流量大小对液位开关的动态响应将产生影响。

4 不确定度评定

不确定度用于表征由随机影响引起的被测量值的分散性。标准不确定度一般由单次测量实验标准差s来衡量[14-15]。

通常认为，由于液位开关等效电路近似为一阶系统，且动态响应呈近似单调线性的特征，故在不直接测得液位开关的时间常数时，可以通过测量液位开关对距离的响应来间接反映其动态响应性。因此采用测距的办法来评定其动态响应不确定度。

测距的数学模型为

δ=h-hs

(13)

式中，δ为液位开关测得距离的误差；h为液位开关离开液面时由步进电机测得的距离(读数)的单次测量值；hs为标准距离。

灵敏度系数为

(14)

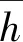
不考虑hs的不确定度，则按3.2节方法对被测液位开关重复测量n次，测得值为hi(i=1,2,…，n)，则其单次测量实验标准差为

(15)

设容器上一共安装了m个液位开关，得到s1,s2,…,sm，取最大值，即

smax={s1,s2,…,sm}

(16)

则液位开关动态动态响应A类标准不确定度为

u(h)=smax

(17)

若容器标定时，测得两个液位开关的距离为H，不确定度为u(H)，则装置液位开关引起的合成不确定度为

(18)

取置信概率p=95%，扩展不确定度为

U95=t95·uc(δ)

(19)

在单独的测试系统中，设两个液位开关距离最小距离为Hmin，则液位开关的相对不确定度为

(20)

若不计u(H)，取置信概率p=95%，则扩展不确定度为

U95=k95·uArel(h)

(21)

以图7测得数据为例，最大单次测量实验标准差为0.017%，其扩展不确定度为U95(h)=2×0.017=0.034%(k95=2)。

5 结束语

对JJG 164—2000采用的液位计的动态响应检定方法进行了分析，讨论了一种新的针对变水头流量标准装置液位开关的动态响应不确定度评定方法。通过建立被测电容式和导纳式液位开关的动态响应理论模型，得出相同条件下，相较电容式液位开关，导纳式液位开关可以有效消除粘附层影响，精确度更高，但时间常数却略大于电容式液位开关。总结归纳了液位开关单独测试和在变水头流量标准装置使用所引发的不确定度评定方法，使用新的不确定度评定方法进行实验，结果显示，被测电容式和导纳式液位开关的动态响应不确定度基本相当；但随着液面下降速度增加，即变水头流量标准装置的工作流量增大时，其不确定度也有增加的趋势。当液面下降速度为1.2 m/min时，在不考虑液位开关距离不确定度的情况下，被测电容式液位开关的扩展不确定度为0.034%。