声速误差对平面波成像质量的影响

张静雅，樊尚春，屈晓磊

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

X线CT(Computer Tomography，计算机断层扫描)、MRI(Magnetic Resonance Imaging，磁共振成像)、ECT(Emission Computed Tomography，发射计算机断层显像)以及医学超声成像技术[1]，是现代医学四大影像技术。与MRI、X线CT和ECT这3种技术相比，超声成像技术的突出特点是无电离福射，其用于医学临床诊断时具有成本合理、便携性、无伤害等优点，同时它又能提供人体断面的实时动态图像[1]。在超声成像领域，近年来出现了新技术——超声平面波超快速成像技术。对于许多需要在很短时间内获得图像的超声成像应用来说，超快帧速率至关重要，例如捕获心动周期中的心跳、检测血流速度并跟踪弹性成像中的剪切波的传播[2]。若不使用平面波技术，可能无法达到每秒数千帧的超高帧速率，所以平面波技术在弹性成像、血流速度等领域中得到广泛运用[3]。

1977年，Bruneel等[4]首次提出超快速成像的概念，使用了光学概念处理超声信号的超高速回波成像系统。1979年，Delannoy等[5]又提出在该系统的接收端使用模拟并行处理器，从而可以在超声发射的同时得到整幅图像，1 s内可以获得1000帧图像，每幅图像有70条扫描线。1984年，Shattuck等[6]完善了并行处理的方法，使用相控阵扫描仪通过在体实验得到了验证。1990年，Sandrin等[7]研制了模数转换器的时间反转镜技术实现了并行处理，并提出了使用平面波发射和通过并行接收波束形成接收的高速超声成像概念。后来，Cheng等[8]提出空间上以相干或非相干的方式复合不同转向角度的平面波，提高图像的分辨率、减少散斑。20世纪80年代初，Berson等[9]提出医学成像中的超声复合平面波成像，通过改变换能器发射角度或者频率，叠加多幅图像得到复合图像，从而提高信噪比。2005年，Jensen等[10]提出合成孔径法，用不同角度获得图像的相干平面波复合。

成像区域各组织的声速都大不相同，从脂肪组织的1450 m/s到肌肉组织的1600 m/s[11]，但是大多临床超声成像系统都采用统一固定的假定声速进行成像，该声速通常为1540 m/s[12]。假定声速和真实声速之间的偏差会造成超声图像的空间相位偏移和散焦，从而降低图像的质量。空间相位偏移是因为使用了假定声速计算目标与换能器之间的距离，散焦是因为接收波束和发送波束形成延迟模式都是使用假定声速设计的。波束形成延迟模式的误差可能会导致波束焦点空间上的偏移。接收束焦点的空间移位会使点扩散函数变宽，并改变超声图像中散斑的统计特性[13]。由于空间相位偏移和散焦会降低图像的质量，故研究声速误差对平面波成像质量的影响具有重要意义。

1 方法

1.1 平面波成像

1.1.1 成像基本原理

在传统B-mode成像中，每条波束是通过一组换能器施加脉冲产生单个聚焦波束，如图1(a)所示，最终图像是将所有波束聚集在一个矩阵中，使用希尔伯特变换执行包络检测[14]。

平面波成像(Plane Wave Imaging,PWI)不同于传统的B-mode成像。首先，超声波束在PWI中不聚焦，即焦点位于无穷远处；其次，使用所有的换能器元件作为发射器和接收器，而不是只选择其中一部分作为发射孔径。图1(b)为平面波成像示意图，N个传感器(通常为128个)排列成线性阵列放置在被测介质上，x向平行于线性阵列，z向为图像深度方向，垂直于线性阵列方向[15]。

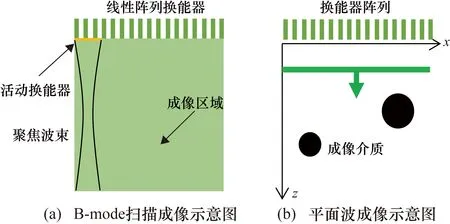
图1 超声光束原理图

在平面波成像中，通过并行处理单次声波脉冲生成一整个帧，声波因介质的异质性产生反向散射现象，阵列接收回波信号RF(x1,t)。因为发射波束没有聚焦，所以图像分辨率只能通过并行处理获得。平面波发射示意图如图2所示。

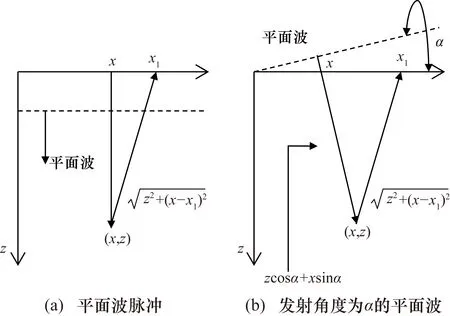
图2 平面波发射示意图

对于平面波脉冲，如图2(a)所示，从点(x,z)返回到x1位置处的换能器的传播时间为

(1)

假定c为介质中传播的恒定声速，图像中每个点(x,z)的强度通过叠加每个相干散射点的贡献获取，根据τ(x1,x,z)对回波信号RF(x1,t)进行延迟，并在延阵列x1方向上相加。

(2)

孔径宽度为2a，孔径必须考虑所有对信号有贡献的换能器元件，并且孔径宽度总是小于换能器阵列L的总长度，成像深度和孔径宽度的比值F称为F-number，计算公式为

(3)

F-number的可行性取决于阵列的方向性(典型值在1～2之间)，理想情况下F-number在整个图像中必须恒定。动态孔径随着图像深度的增加而增加，从而保持F-number的恒定，直到无法增加孔径宽度为止[16]。

1.1.2 复合平面波

由于平面波成像时波束没有焦点，因此图像对比度和分辨率降低。为了提高PWI的成像质量，Berson等提出复合平面波(Compound Plane Wave Imaging,CPWI)技术，通过使用相干或者非相干的方式，复合或者平均由多个特定角度未聚焦波束生成的PWI图像，实现最终图像[16]。

如图2(b)所示，发射一个倾斜角度为α的平面波，则到达点(x,z)的时间为

(4)

声波从点(x,z)返回到x1位置处，换能器的传播时间为

(5)

当平面波具有一定转向角度时，总的传播时间为发射延迟时间和接收延迟时间的总和：

τ(α,x,z)=τec+τrec

(6)

如式(6)所示，对延迟信号求和的波束形成操作称为“延迟叠加”波束形成技术(Delay-and-Sum,DAS)[17]。在CPWI中，复合操作是在不同角度的波束形成之后进行的，CPWI的复合操作可以是相干也可以是非相干的。在非相干CPWI中，分别对每个角度的信号进行包络检测，然后对所有信号进行复合操作；在相干CPWI中，先对所有波束信号进行复合操作，然后再进行包络检测[15]。本文使用相干CPWI。

1.1.3 声速误差对波束形成的影响

首先，分析假定声速和真实声速的误差对超声波束形成的影响。由式(6)可得，每个位置发射波束的延迟时间中的速度c使用的是假定声速cs，生成的波束焦点为F0，如图3所示。设真实声速为cr，则对应的真实发射波束聚焦深度F1为

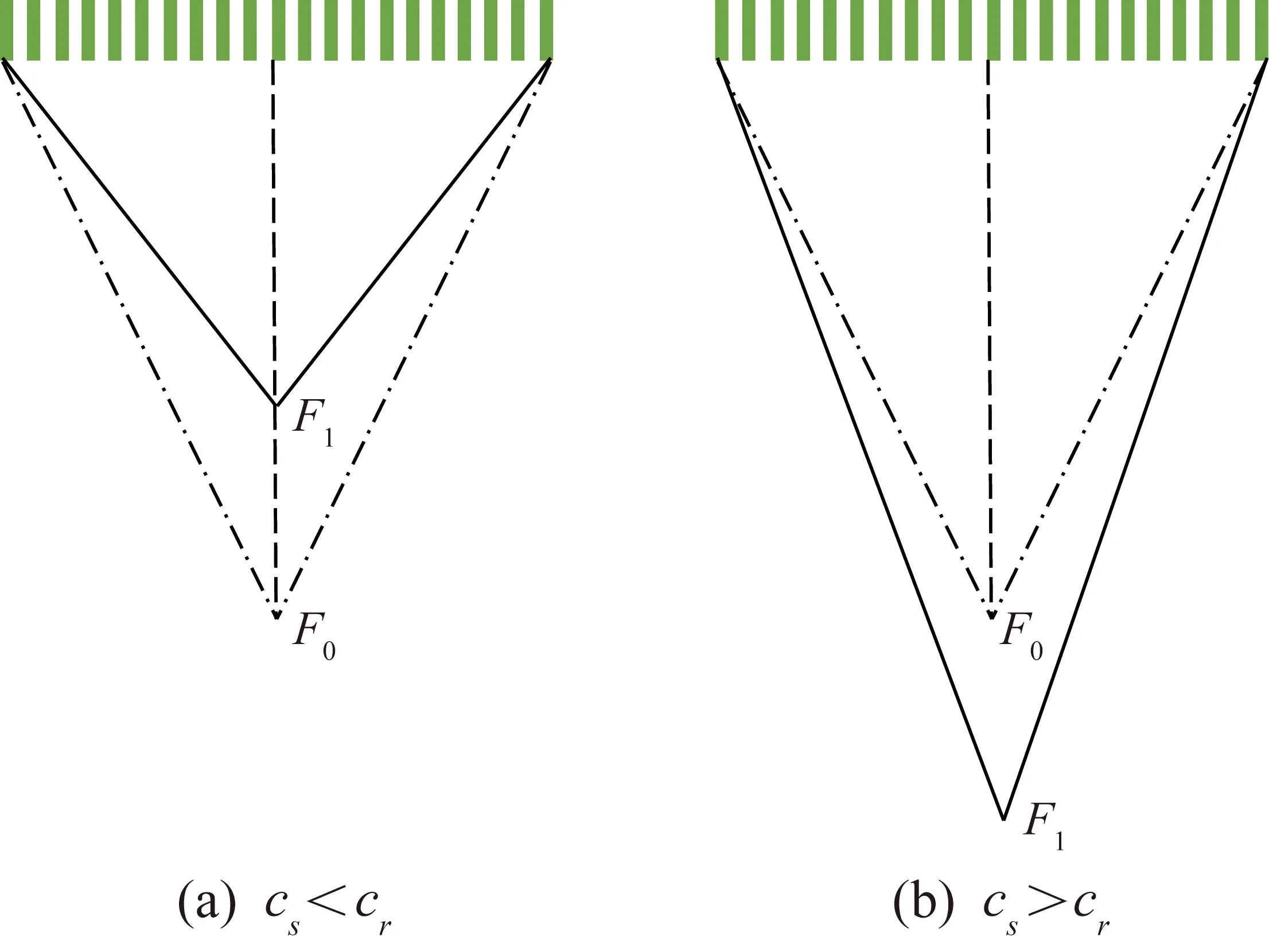
图3 超波束焦点的空间位移

(7)

对于真实接收波束，焦点的空间深度F2为

(8)

超声波束在真实聚焦深度处最窄。因为真实光束焦点与假定光束焦点之间存在空间偏移，所以由假定声速计算出的焦点深度处波束的宽度比真实声速计算出的宽度要宽。空间偏移越大，真实波束的宽度将在假定聚焦深度处越宽。

对于单发射焦点和动态接收焦点的平面波图像，焦点质量主要取决于接收波束宽度，该宽度受动态接收波束形成导致的声速误差的影响。当点扩展函数(Point Spread Function,PSF)直径增加时，超声图像的聚焦质量会降低。PSF的直径由脉冲回波的波束宽度决定，脉冲回波波束宽度由发射和接收波束宽度共同决定，计算公式为[18-19]：

(9)

式中，widthPE为脉冲回波波束宽度；widthT、widthR分别为发射和接收波束宽度。

式(9)解释了如何将发射和接收波束宽度转换为脉冲回波波束宽度。在常用的深度情况里，接收波束都比发射波束窄得多，所以，脉冲回波波束宽度主要取决于接收波束宽度。为节约计算量，在本文中仅接收波束使用了不同的假定声速，采用动态接收波束来获得具有不同聚焦质量的超声图像。在下文中将定量分析真实声速和假定声速误差对超声图像质量产生的影响。

1.2 成像质量评估

1.2.1 对比度

对比度(Contrast Ratio,CR)是超声图像中相邻的两个能够加以区别程度的结构的量度，即图像中两个不同亮度区域的量度之比，CR的值越大，图像对比效果越好，质量越高。其计算公式为

(10)

式中，μ1、μ2分别为两个不同亮度区域的平均强度值。

为了评价图像不同亮度区域的对比程度，引入另一个评价标准：对比噪声比(Contrast-to-Noise Ratio,CNR)，它是图像中两个不同亮度区域的标准偏差之比CNR的值越大，图像对比效果越好，质量越高。其计算公式为

(11)

式中，σ1、σ2分别为两个不同亮度区域的标准差。

1.2.2 PSF

PSF描述了一个超声成像系统对一个散射点的响应，用于测量超声系统空间分辨率的评估效率，从而评估成像的质量。为了进行分辨率的评估，将散射点图像以局部极大值一半为阈值进行分割，在各向同性的介质中，该分割区域为圆形，其直径可以视为PSF的直径[20]，PSF的直径越小，分辨率越高，图像质量越好。

2 结果

为了定量评估声速误差对平面波成像质量的影响，利用Matlab的k-wave工具箱进行仿真实验，这是一个高效的工具箱，用于在复杂且组织真实的介质中进行时域超声仿真。在本实验中，设置128个宽度为0.25 mm、高度为5 mm的换能器，其中心间隔为0.3 mm，均匀地排成线性阵列。声波的中心频率为2 MHz，超声图像宽度和深度均为40 mm。转向角范围设定为-20°～20°，复合角个数为17，F-number的值为1。

2.1.1 均一介质

为了利用CR、CNR和PSF定量分析声速误差对平面波成像质量的影响，实验设置两个模型：① 背景声速为1540 m/s，密度为1020 kg/m3，设置一个长为40 mm、宽为20 mm的矩形高回声囊性区域，其声速均值为1540 m/s，密度为1020 kg/m3，标准差为3%。② 背景声速为1540 m/s，密度为1020 kg/m3，设置9个散射点，纵向排列，间隔均为2.5 mm，声速为2000 m/s，密度为1333 kg/m3。

真实声速为1540 m/s，将假定声速和真实声速之间误差设置以10 m/s为间隔，范围为-100～100 m/s，分别根据模型1和模型2的设置进行仿真，如图4所示。根据图4(a)，分别划分长为25 mm、宽为12 mm的矩形高回声区域(红色矩形区域)和长为25 mm、宽为12 mm的矩形背景区域(黄色矩形区域)，不同假定声速下囊性模型的CR和CNR如图4(b)、图4(c)所示。

由图4(b)、图4(c)可以看出，当声速误差为0时，超声图像的CR和CNR最大，随着假定声速和真实声速的误差增大，图像的对比度下降。

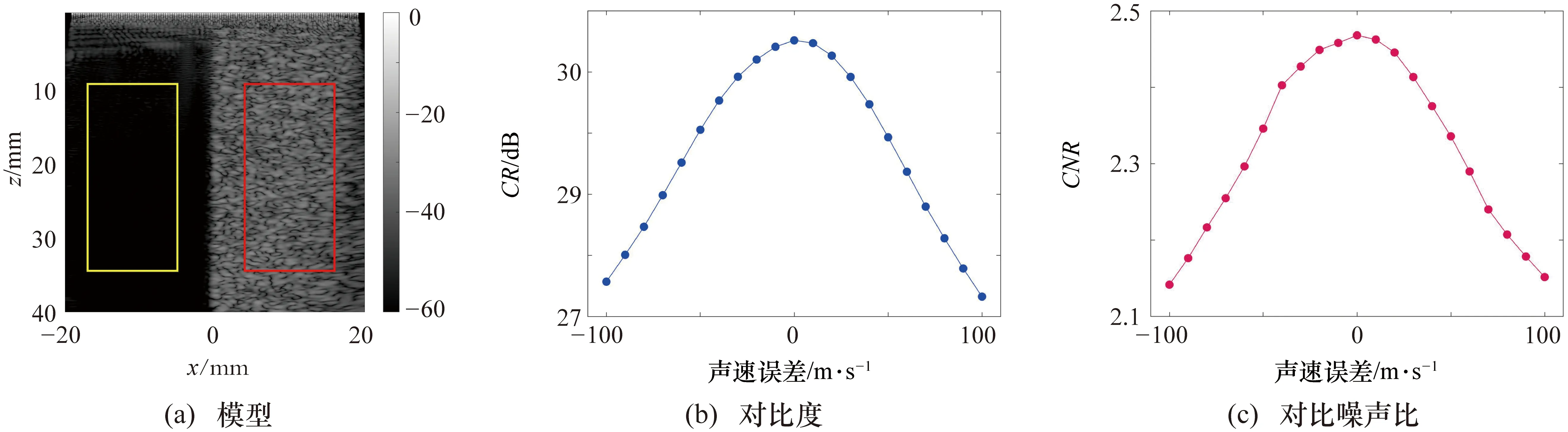
图4 不同假定声速下均一介质模型的对比度

不同假定声速下均一介质模型的PSF如图5所示。

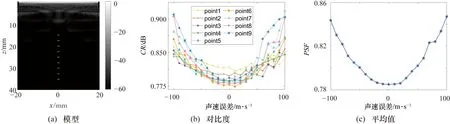
图5 不同假定声速下均一介质模型的PSF

根据图5(a)，存在9个深度不同的散射点，散射点1～9分别从上到下对应图5(b)中的PSF标号，散射点1～9的PSF大小以假定声速和真实声速之间误差等于0为基准。随着声速误差值的增加，PSF的直径以声速误差等于0为基准向两边递增，随着声速误差值的增加，PSF的直径增加；图5(c)中曲线为9个散射点PSF的平均大小，可知随着声速误差的不断增加，PSF的直径不断变大。

2.1.2 复杂介质

为了模拟真实的乳房声速分布，使用LabelMe软件将6个不同的2D MRI真实图像分割为皮肤、腺体和脂肪区域，然后分别为其分配声速1600 m/s，(1570±7.85)m/s和(1470±1.47)m/s(平均值±标准差，7.85是1570的0.5%，1.47是1470的0.1%)。假定声速设定为1540 m/s。为了更加符合实际，设置模型尺寸为40 mm×40 mm，如图6所示，这些乳房模型具有不同的形状、大小和乳房密度(腺体与脂肪组织的比率)。

图6 分割6个不同的MRI乳腺图像的声速模型

为了定量分析复杂介质下声速误差对平面波成像的分辨率和对比度的影响，通过k-wave工具箱仿真得到6个不同乳腺声速模型的DAS图像结果，如图7所示。

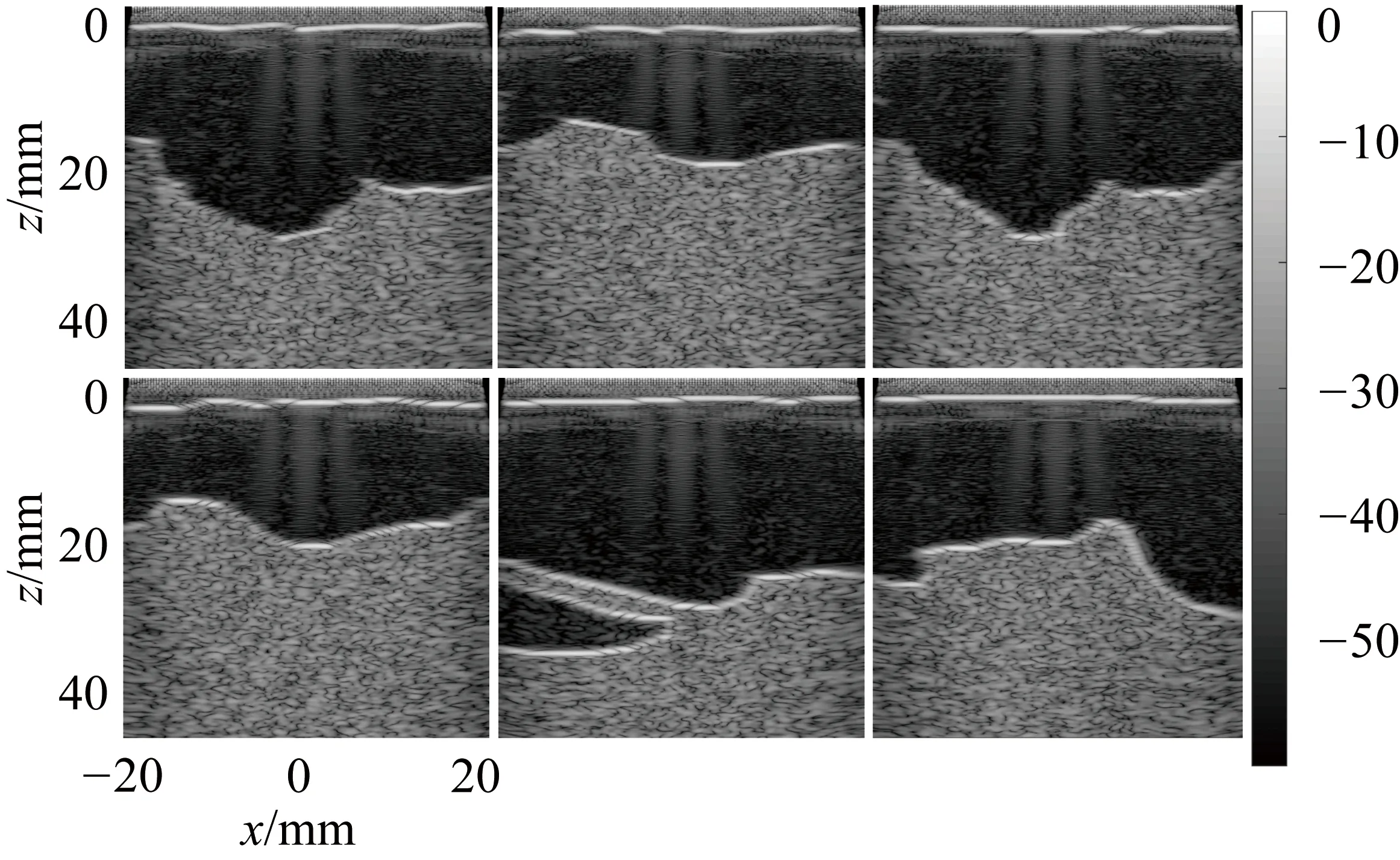
图7 不同乳腺声速模型生成的DAS图像

以模型1为例，为了进行分辨率评估，在声速模型中放置了3×12个具有极高声速的散射点，如图8(a)所示，散射点速度2000 m/s，间隔为2.5 mm。为了进行对比评估，在脂肪和腺体组织区域放置了随机散点。

图8(b)给出了具有随机散射点的声速模型的示例，脂肪和腺体组织区域的声速值分别为1470 m/s和1570 m/s，其标准偏差分别为0.1%和0.5%，这使得图像中腺组织区域的强度高于脂肪组织区域的强度。

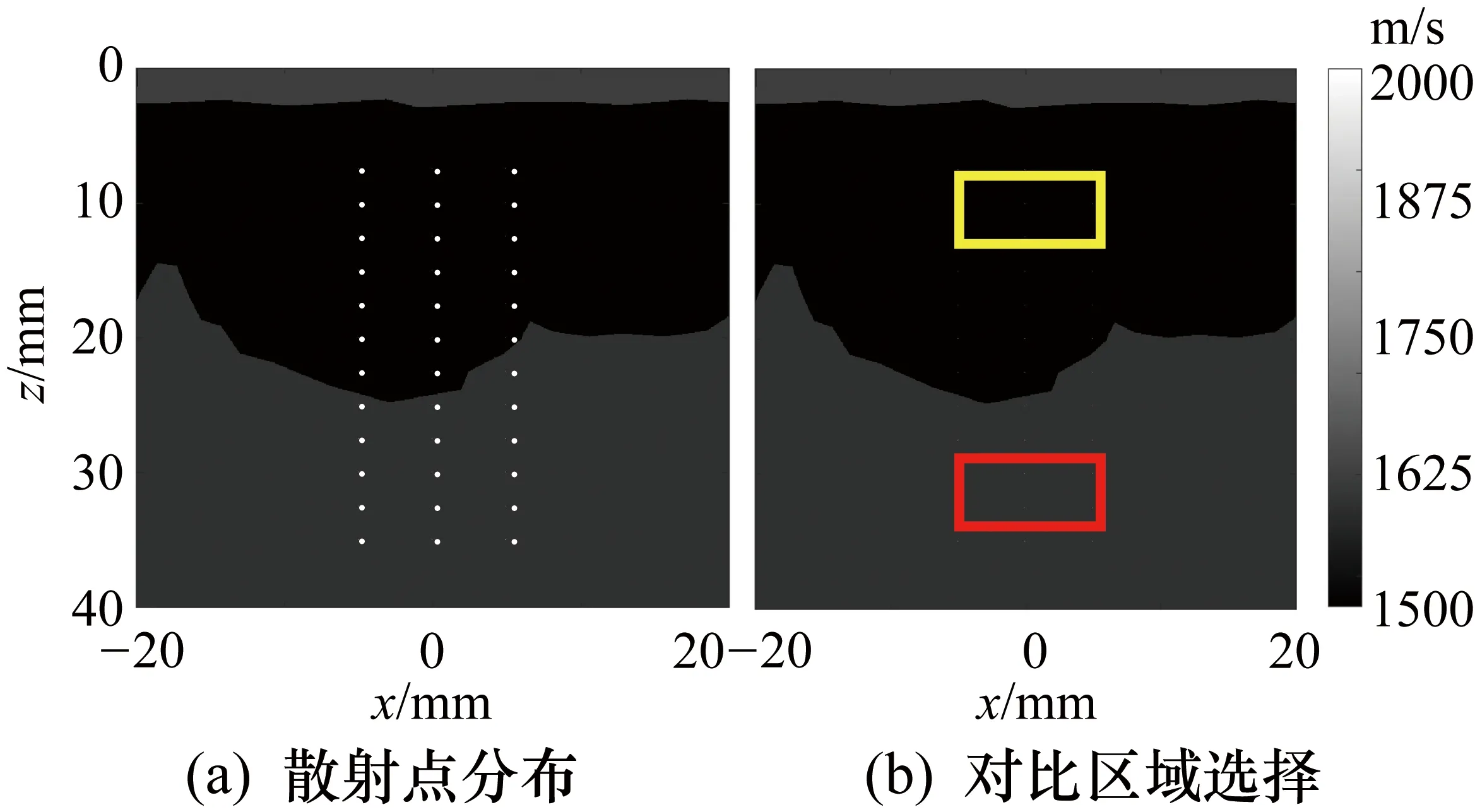
图8 用于分辨率和对比度评估的速度模型

根据图8(a)中散射点的分布，分别计算6个不同乳腺声速模型中所有散射点平均PSF直径大小，结果如图9(a)所示。根据图8(b)，为进行对比度评估，分别选择腺体组织区域中长为7 mm、宽为4 mm的红色矩形区域和脂肪组织区域中长为7 mm、宽为4 mm的黄色矩形区域，腺体组织和脂肪组织的CR和CNR如图8(b)、图8(c)所示。

由图9(a)可知，复杂介质分布模型的PSF直径大小均值为dPSF=0.93 mm，在均一介质模型中，如图4 (c)所示，当假定声速为1540 m/s，即声速误差为0时，模型的PSF直径大小均值为dPSF=0.90 mm，6个不同复杂介质模型的PSF直径大小均值大于均一介质模型的PSF直径大小；由图9(b)可知，复杂介质分布模型的对比度均值为CR=15.21 dB，CNR=1.34，在均一介质模型中，如图5(b)、图5(c)所示，当假定声速为1540 m/s时，图像的CR=30.51 dB，CNR=2.46，则6个复杂介质分布的模型的CR和CNR均小于均一介质模型中的CR和CNR。

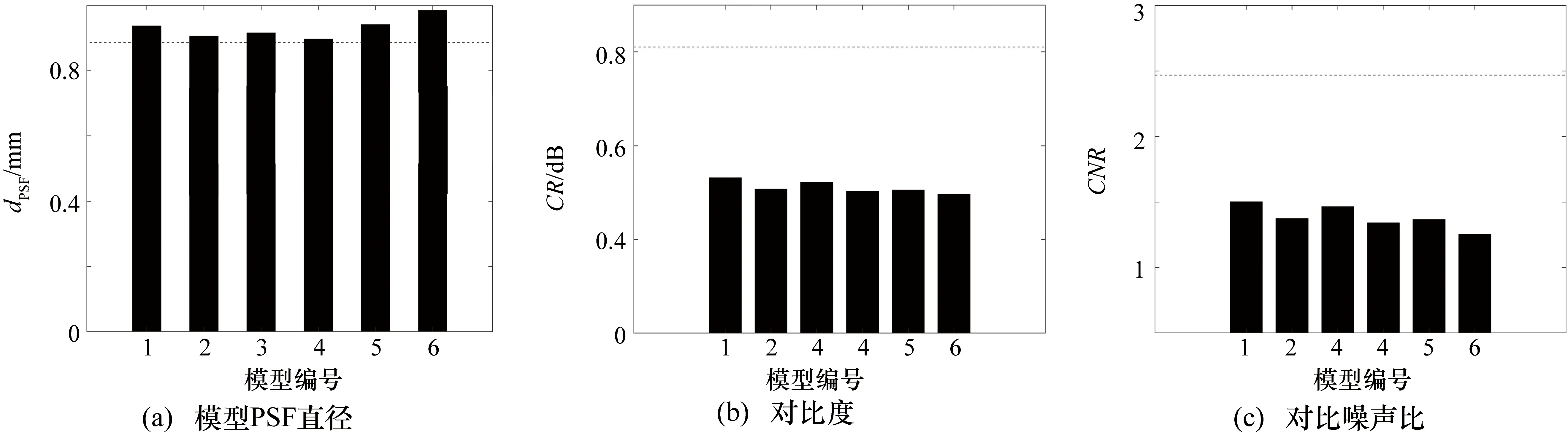
图9 用于分辨率和对比度评估的速度模型

3 结束语

本文研究了在均一介质模型中不同声速误差和复杂介质模型中假定声速对平面波成像质量的影响。通过CR、CNR和PSF定量分析图像的对比度和分辨率，从而评估平面波成像的质量。在均一介质中，当声速误差为0时，模型所设散射点平均PSF直径为0.90 mm，模型不同区域CR=30.51 dB，CNR=2.46。随着声速误差的增加，PSF直径的值变大，CR和CNR的值变小，分辨率和对比度下降，成像质量变差；在复杂介质中，选择6个不同声速分布的乳腺模型，其假定声速均为1540 m/s，平均PSF直径等于0.93 mm，腺体与脂肪区域的CR和CNR均值分别为15.21 dB和1.34，则假定声速下复杂介质模型的PSF大于真实声速下均一介质模型的PSF直径，其CR和CNR小于真实声速下均一介质模型中的CR和CNR，其分辨率和对比度下降，即由于假定声速和真实声速的差异，复杂介质模型的成像质量比均一介质模型中使用正确声速的成像质量差。