片上电源电压噪声功率谱测量方法综述*
翟鹏飞 ,周 雄 ,李 强 ,2
(1.电子科技大学 电子科学与工程学院,四川 成都 610054;2.琶洲实验室-人工智能与数字经济广东省实验室,广东 广州 510330)
0 引言
现代的片上系统(SoC)的功能越来越复杂,性能要求也在不断提高,为了保证系统良好稳定地工作,其电源网络是十分复杂的。随着工艺尺寸越来越小,片上走线和走线、走线和器件之间的寄生越来越大,相互之间的耦合和干扰也就越来越大,更加恶化了片上电源噪声的情形。同时,电源供电电压越来越低,导致噪声容限越来越小,所以电源网络模型在芯片的设计过程中是十分重要的。要想获得准确的电源网络模型,需要在芯片生产出来后,对芯片内部的电源电压噪声(PSN)进行实际测量,再由测得的噪声数据反推出电源网络模型的参数。
片上PSN 测量类型主要可以分为时域波形测量[1-4]和噪声功率谱测量两种[5-9],本文主要介绍片上噪声功率谱测量技术。片上电源电压功率谱测量主要是基于维纳-辛钦定理,对电源电压上的周期平稳噪声进行测量[6],以得到噪声的频率和幅度信息。根据这些信息,同时也可以进一步确定噪声源的位置,并预估其对芯片中各个模块性能的影响。
1 噪声功率谱测量原理
PSN 本质上是由于电源网络下的负载中的开关快速切换产生了变化的电流流经电源网络中的寄生电感、电容和电阻,在芯片内部电源上所产生的变化的电压[10]。因为在频域上PSN的频率范围非常宽,可以从接近DC的极低频到100 GHz的极高频[4],导致很难采用模数转换器(ADC)来直接采样量化。幸运的是,由于PSN 主要部分是因为受系统时钟触发的电路周期性地开合所引起的,使得这部分的噪声可以被看作一个具有周期平稳特性的随机过程,所以根据维纳-辛钦定理可以通过测量噪声的自相关函数,再经过傅里叶变换后就可以测得噪声的功率谱。
电压噪声的自相关函数R(τ)定义为:

其中x(t)为电源电压,TS为采样时钟周期,n 表示第n 次采样,τ 代表两次噪声采样的时间间隔,E[]表示求期望。假设x(t)为单频点的周期函数,它的自相关函数为R(τ),当τ 等于0 或者x(t)周期的整数倍时,R(τ)达到最大值;所以R(τ)完全包含了x(t)的周期和幅度信息。对于一个周期平稳的噪声信号,其中可能包含多个频率分量,通过扫描τ的值,计算不同τ 值下的自相关函数值,就可以把函数中所有的频率分量和该频率分量对应的幅度信息测量出来。测量系统的奈奎斯特(Nyquist)带宽是由τ的变化步长决定的。
2 基于自相关函数的测量技术
基于自相关函数的测量技术目前在片上测量噪声功率谱的应用领域中属于主流技术。通过上一节的介绍可以看出,这种测量技术的Nyquist 带宽是由两个采样时钟之间的时间间隔τ的变化步长所决定的,而不是由采样时钟周期TS决定的。例如设计Nyquist 带宽是20 GHz,则τ的变化步长需要小于25 ps,采样时钟的周期TS理论上可以是任意值,但为了综合考虑测量时间和电路设计难度,一般TS设定在10 ns~1 μs 之间。所以可以利用这一特点,用两个低速的自相关采样时钟触发两路采样量化电路,就可以测得高频噪声信号的功率谱,并且不会出现混叠现象。
图1 是基于自相关的测量噪声功率谱的电路模块图,其中包括自相关时钟产生电路和两路采样与量化电路,以及用于计算自相关函数的数字电路。
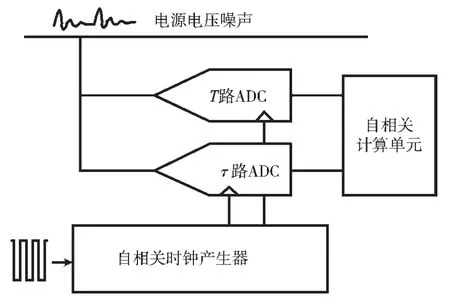
图1 基于自相关函数测量技术的电路模块图
2.1 自相关时钟产生电路
自相关时钟可以选择从片外输入[6-7]和片上产生[5,8]两种方式,这两种方式都需要时钟产生电路。片外输入的主要优点是可以节省芯片的面积和功耗,以及降低设计难度,容易纠错与校正;主要缺点是增加了测试电路板的设计复杂度。片上产生的优缺点与片外输入的相反。因为自相关时钟片上产生电路排除故障难度较大,近几年才有文献将这部分电路做到片内,并取得了很好的测试效果[5,8]。
图2 是两路自相关时钟产生电路的示意图,它由一个多相位时钟产生器和一个时钟控制器组成。多相位时钟产生器是将一个输入参考时钟通过延迟器单元产生频率相同相位不同的一组时钟,需要保证最小的延迟等于τ的变化步长。
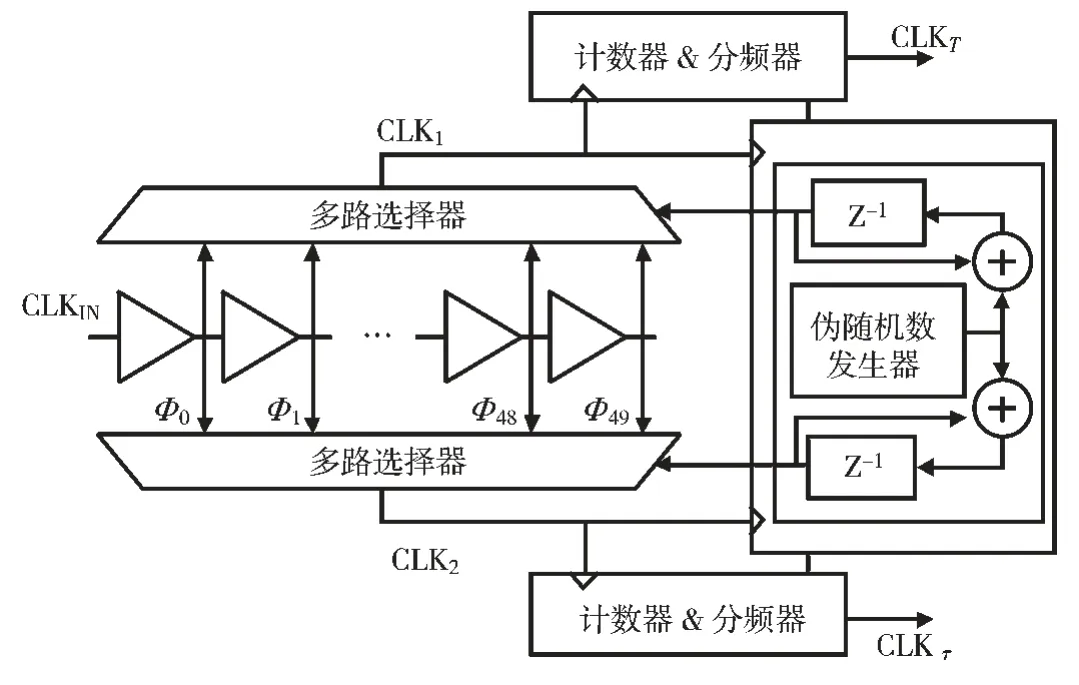
图2 自相关时钟产生电路模块图
时钟控制器的功能是从这组多相位时钟中选择出来两组符合自相关采样要求的时钟。如图3 所示,T 路时钟和τ 路时钟开始保持时间差为τ1,经过N 个周期之后,τ 路时钟的延迟增加25 ps,此时与T 路时钟的时间差变成τ1+25 ps,再保持N 个周期之后,τ 路时钟的时间差再增加25 ps,以此类推,直到采到m 个采样点。m 是由频谱分辨率决定的,比如Nyquist的带宽是20 GHz,频谱分辨率为10 MHz,那么m 等于4 000。N 是求自相关运算时的平均数,N 越大,得到的功率谱噪底越低。选出的两路时钟经过分频器之后,得到了两路低频时钟再送到两路采样量化器。
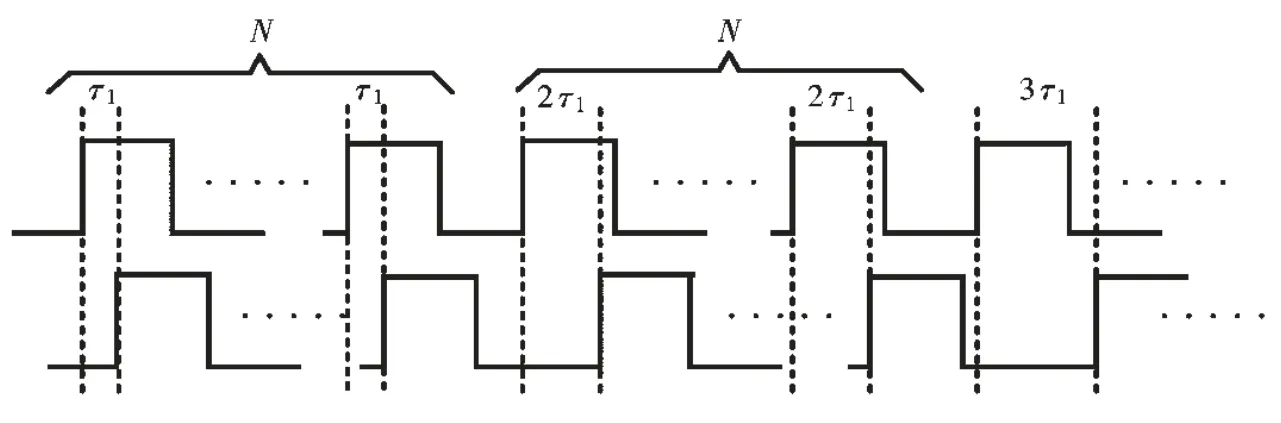
图3 自相关采样时钟示意图
2.2 采样与量化电路
文献[6]中最早完成了基于自相关的噪声功率谱片上测量电路。电路的主要部分是两路一样的采样保持与量化电路,其电路结构如图4(a)所示。被测电源电压作为采样保持电路的输入电压,采样开关由上一小节介绍的采样时钟控制,再通过buffer 把采样电压缓冲到压控振荡器(VCO)的控制端,使VCO的振荡频率和采样的电压成正比。然后将VCO的输出端送给计数器,在一个固定的计数时间窗内完成计数,最后得到的计数值和被测电源电压成正比。
图4(b)是量化器工作的时序图,其中Samp 是采样时钟信号,低电平阶段完成采样,高电平阶段是保持阶段,同时高电平阶段也作为计数器的计数时间窗TWIN。在保持阶段,VCO的输出电压触发计数器进行计数,在下一次采样时钟下降沿来的时候,完成计数,并将得到的码字送到后续的自相关计算模块中。
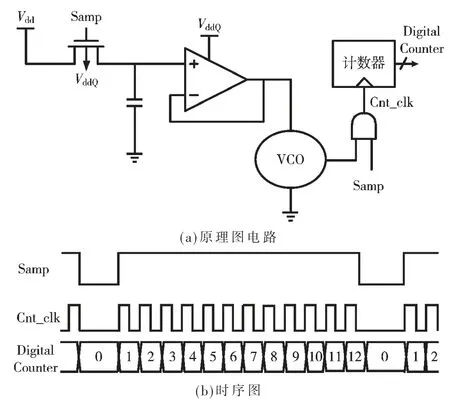
图4 适用于电源噪声测量的采样与量化
这种量化器的结构的精度和固定时间窗TWIN以及VCO的增益KVCO成正比:

也就是说,提高测量精度,一是可以通过提高KVCO;二是可以通过增加TWIN的长度,但增加TWIN会导致测量时间增长。
3 基于Dither的平均值测量技术
上一节介绍的用于量化PSN的高精度量化器,由于高精度的量化过程需要较长的保持时间,因此在量化器之前需要一个采样保持电路。为了使保持的电压不受被测电源信号干扰,需要采样开关的衬底端接到一个额外的干净的电源上。同时,为了避免量化器部分被干扰,也需要为其提供一组干净的电源和地。这使得将量化器嵌入到被测电源域的同时还需要接入一组干净的电源和地,在高密度的现代SoC 中这种操作会增加布局布线的复杂度。为了避免使用干净的电源,文献[7]中提出一种基于Dither的低精度量化器,通过多次测量计算其平均值,依然可以得到高精度量化结果。这种方法本质上是通过降低单次量化精度来减少一次量化所需的时间,在这个极短的量化时间内被测电源电压来不及变化,可以被看作一个固定值。
3.1 基于Dither的1-bit 量化器原理
图5 展示了基于Dither的用比较器做1-bit 量化器的工作原理。考虑一个理想的比较器,它的两个输入端,一端接被比较的电压信号,另一端接稳定的参考电压。如果被比较信号不变,比较器每次量化结果都不会改变,得到的信息只有被测电压信号大于或者小于固定的参考电压,而具体大多少或小多少无从得知。但是如果把稳定的参考电压上叠加一个均匀分布的Dither 信号,保持输入信号不变,进行充分多次比较,将比较结果相加后求平均值,这一测量结果VMEAS 就会更接近被测电压的真实值:
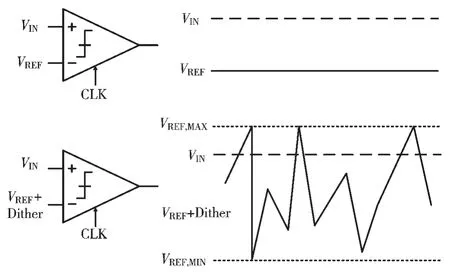
图5 基于Dither的1-bit 量化器的工作原理
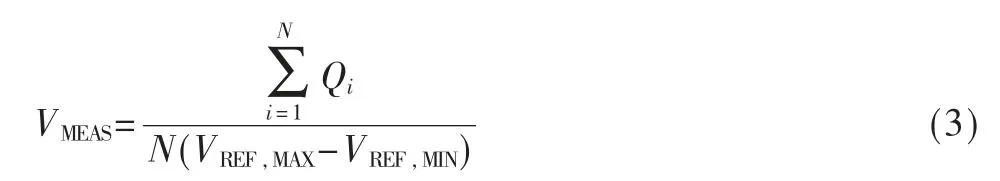
其中Qi是第i 次的比较结果,VREF,MAX是参考电压加上Dither的最大值,VREF,MIN是参考电压加 上Dither的最小值,N 是比较次数。需要注意VREF,MIN到VREF,MAX的范围要大于被测电压信号VIN。
当被测电压是带有噪声的电源电压时,即VIN是一个变化的信号,此时对一路信号进行多次量化之后再对量化结果求平均值,这个平均值只能代表变化的VIN在这段时间内的平均值。但是应用于测量自相关时,文献[7]证明了当被测电源电压不是稳定的,即含有噪声分量,它的R(τ)依然可以通过基于Dither的1-bit 量化器测得,如式(4)所示:

其中Qti是T路的量化结果,Qτi是τ路的量化结果,k的值为VREF,MAX-VREF,MIN。
3.2 基于Dither的1-bit VCO 量化器
图6 给出了一种用于测量PSN的基于Dither的1-bit VCO 量化器[7]。这种结构的工作原理和上一小节介绍的基于Dither的比较器作为量化器的理论基础是一样的。将比较器换成了VCO 量化器结构时,可以避免给量化器提供干净的电源。具体的工作原理是将VCO 直接嵌入被测电源域中,使得VCO的振荡频率和电源域中的噪声成正比,再通过两个触发器检测在固定时间窗TDelay内是否有时钟的上升或下降沿。如果有沿,异或门的输出为“1”,否则为“0”。由于VCO的振荡频率越快,检测到时钟沿的概率越高,因此“1”出现的概率和被测PSN的电压成正比。
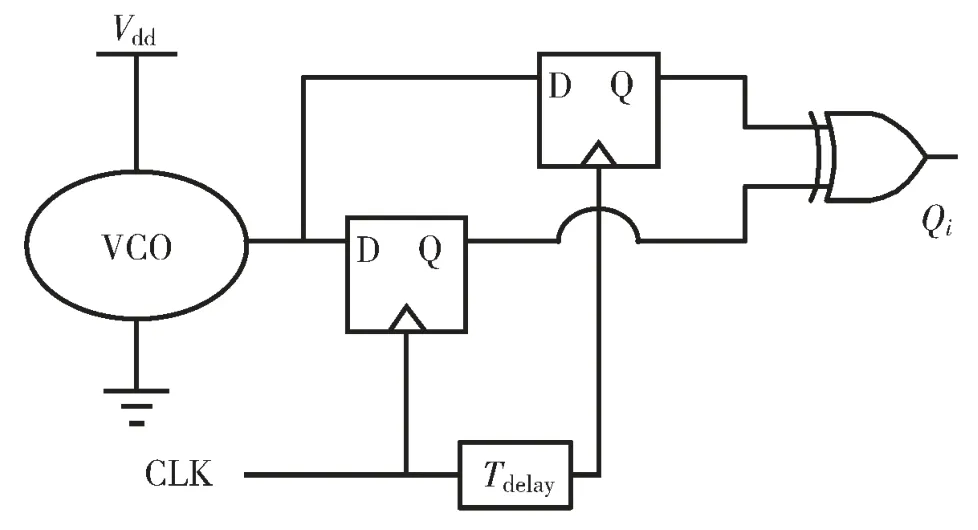
图6 基于Dither的1-bit VCO 量化器
与图5 不同的是,VCO 量化器有三个主要优点:一是由于VCO自身的相位噪声和采样时钟不相关,采样时刻的初始相位是个随机量,可以看作一个自然的Dither源,而不需要额外产生Dither的电路;二是VCO 结构可以做成基于反相器的结构,有很高的数字化特点,使得电路设计较为简单,而且对工艺尺寸的缩小有很好的兼容性;三是这个结构由于电源和地的电压抖动都可以影响VCO的振荡频率,因此测得的是被测电源域中电源电压噪声与地电压噪声的差值,而不是单纯的电源电压的噪声。
4 结论
本文分析了基于自相关函数来测量电源电压噪声功率谱的原理,介绍了具体的电路实现,包括适用于自相关采样的时钟产生电路和量化电路,同时也介绍了为了避免在量化器部分应用干净的电源而提出的基于Dither的低精度量化器技术。这些原理和技术为片上测量电源电压噪声的功率谱提供了解决方案。

