小天体表面纹理曲线精准匹配算法

王光泽，邵 巍，郗洪良，姚文龙，黄翔宇

（1.青岛科技大学 自动化与电子工程学院，青岛 266100；2.北京控制工程研究所，北京 100094）

引 言

近年来，各国纷纷开展了小天体着陆与采样返回任务[1-2]，为获得有价值的科学素材，需要探测器着陆到具有较高的科学价值的特定区域，这就需要探测器具备精确导航的能力。视觉导航是目前发展较为成熟的自主导航方法，并在各种深空探测任务中得到不同程度的发展与应用，其利用光学敏感器件获取天体及其表面图像，通过图像中提取的特征来确定探测器空间位置等信息。

当前用于视觉导航的地标主要分为两类。一类是使用图像中的特征点信息进行导航，例如使用角点检测算法来估计检测器的速度[3-5]，Bakambu等[6]提出这类算法通常不如使用图像区域匹配稳定。特征点反映的信息量远低于边缘特征曲线，尤其对于多尺度特征点，存在无法与图像中物理纹理相对应的情况，其应用场景受限。

另一类是将天体表面的岩石和火山口等自然特征用作导航陆标。同时，这些特征还能在着陆阶段用于障碍物躲避。许多学者对陨石坑的探测和匹配方法做了很多研究[7-9]。这些算法中大多数都使用陨石坑形状、阴影等信息进行匹配，在处理沟壑、重叠的坑或不规则的岩石时容易发生误匹配[10]。

不规则曲线特征在天体表面普遍存在，可作为导航陆标进行导航。对曲线精准匹配是进行视觉导航的重要前提[11]。国内外众多学者针对曲线匹配方法展开研究。

基于描述符的方法是曲线匹配重要分支。Liu 等[12]通过按亮度划分曲线支撑区域构建了描述符IOCD（Intensity Order Curve Descriptor）。王志衡等[13]为解决描述符主方向难以确定的问题，提出了描述符IOMSD（Intensity Order based Mean Standard Deviation Descriptor），在图像受到模糊、噪声干扰时，可以保持不变性。Chen 等[14]提出梯度阶曲线描述符，对光照变化与噪声干扰有较好的鲁棒性。基于曲线描述符曲线匹配方法根据曲线支撑区域相似度来进行匹配，当局部判断为匹配时，则认为整条曲线匹配，因此基于曲线描述符曲线匹配计算量较小，但难以实现曲线精准匹配。

基于曲率的方法也是曲线匹配重要方向。Cohen等[15]提出使用B样条来近似拟合曲线，通过曲率等曲线特征的计算进一步完成曲线匹配工作。Taniai[16]等提出基于图像分割的空间曲线局部匹配算法，该算法可以得到空间曲线分段描述，并保证了曲线的光滑性[17]。Cui 等[18]通过计算等积分间隔下曲率实现曲线精准匹配，该算法具有尺度与旋转不变性。基于曲率的曲线匹配，适于处理图像中两条曲线匹配问题，当对多条曲线匹配时计算量过于庞大。

为实现曲线精准匹配，提出一种曲线描述符与曲率相结合的曲线精准匹配算法，通过描述符完成曲线粗匹配，再根据曲率完成精准匹配。本文具体结构安排如下：第一部分介绍了多尺度纹理曲线提取算法与曲线描述符构建方法；第二部分在曲线描述符粗匹配基础上，介绍尺度不变曲率计算与匹配；第三部分在光照、尺度及旋转变换下分析实验结果；第四部分对文章进行总结。

1 曲线描述符匹配

1.1 不规则曲线提取

曲线特征提取是匹配的基础，为综合多尺度纹理特征，对原始图像降采样处理，获得一系列不同分辨率图像，建立高斯金字塔模型。

基于Topal等[19]提出的Edge Drawing算法对每层图像分别进行曲线提取。根据边缘像素特点，使用Sobel算子计算梯度图，为加快计算速度，设置阈值筛选像素梯度，剔除小梯度像素。

为获得连续边缘曲线，放弃逐像素点边缘判断的思路，而采用基于节点的方法。首先根据梯度图，选择局部梯度极大值对应像素点作为节点。之后由节点开始进行像素连接，当满足以下条件之一停止。

1）当不处于边缘区域时，即当前像素点经梯度阈值筛选后，属于被剔除部分；

2）当检测边缘重复时，即对所在曲线进行像素连接过程中，当前像素点已被检测过一次。

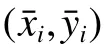
将曲线上所有点变换到原尺度后，对离散点进行线性插值。在原尺度空间，对曲线上相邻两点坐标（x1，y1）与（x2，y2），在区间[x1，x2]上某一位置x处纵坐标取值为+

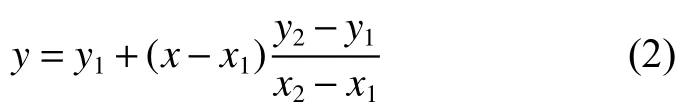
经过坐标变换与插值，高斯金字塔各层曲线提取结果被变换原尺度空间。多尺度曲线提取结果如图1（b）所示，相比单尺度提取结果如图1（a），所得曲线更加全面。同时基于Edge Drawing算法提取的边缘曲线更加连续，并保证单像素宽度，另外曲线基于节点生成，边缘图像噪声较少。

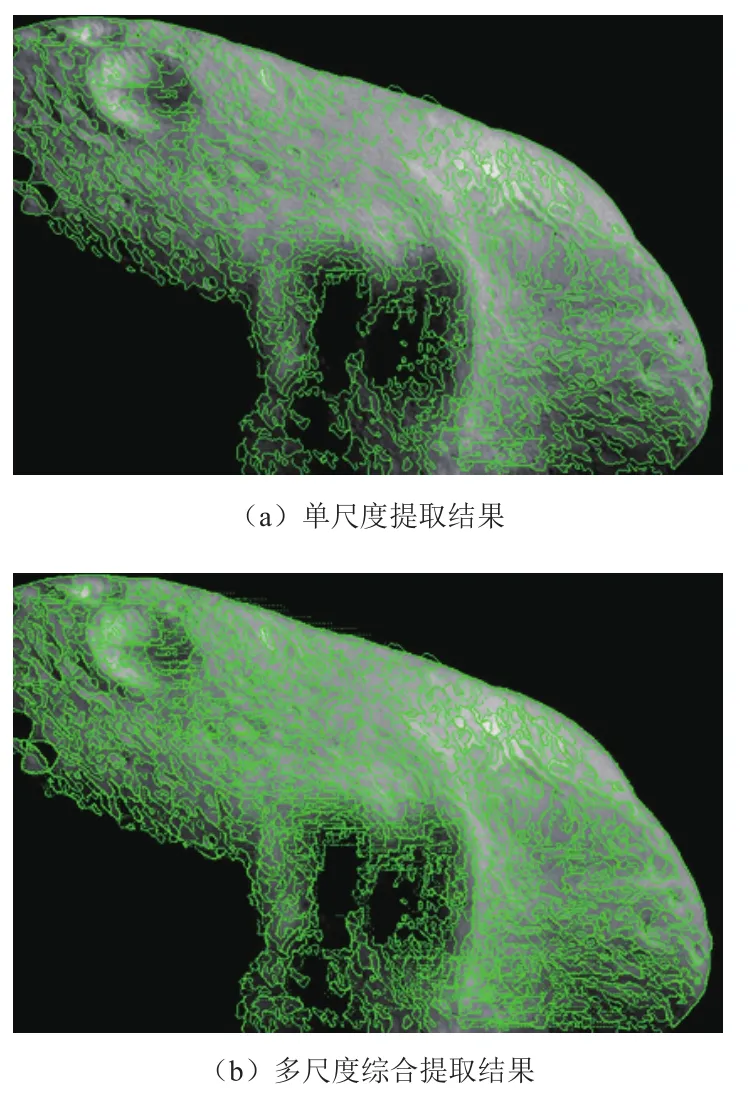
图1 曲线提取结果Fig.1 Curve extraction result

1.2 曲线描述符构建

对曲线进行描述时，采用分段描述的方法，将每段曲线近似作为直线进行描述符构建[10,20]，该描述符包含曲线自身特征同时加入其周围纹理信息，具备良好的辨识性。

描述时，将近似直线两侧区域划分为m条矩形带如图2所示将近似直线两侧区域划分为m条矩形带，记作{B1，B2，B3，···，Bm}，每条矩形带宽度为w，每个矩形带都是曲线支撑区域的子区域。为保证描述符的旋转不变性，将像素梯度向近似直线方向与正交方向投影。假设子区域中某像素梯度值为g，拟合直线方向为dL，与直线正交方向为d⊥，则局部梯度可表示为

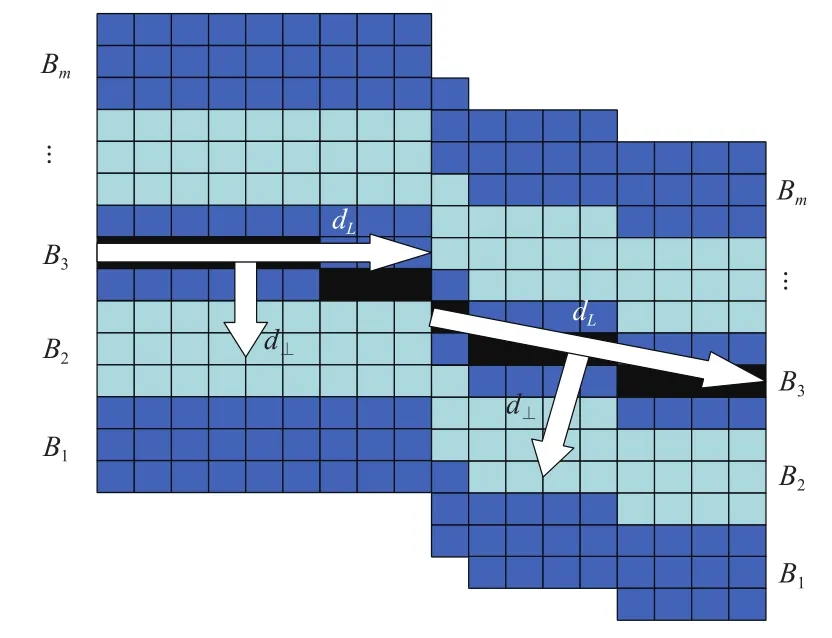
图2 曲线描述符结构Fig.2 Curve descriptor structure

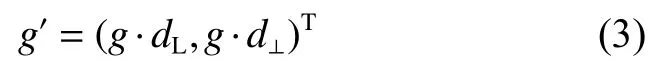
对于第i段曲线支撑区域的Bj矩形带，通过对第k行不同方向梯度值求和可得

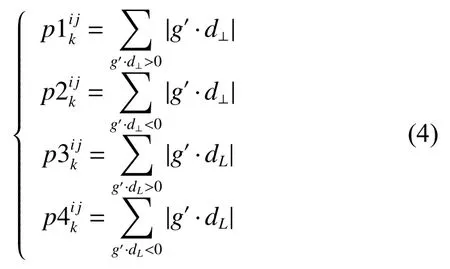
对所有曲线段梯度值求和，可得整条曲线Bj矩形带的第k行梯度信息

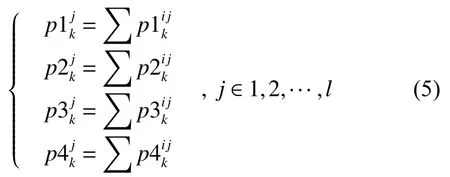
将每行不同方向梯度之和堆叠，可得曲线Bj矩形带梯度矩阵

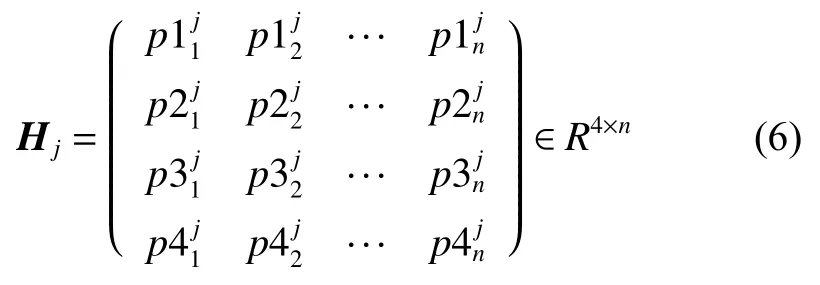
其中：n为计算第j条矩形带所需行数

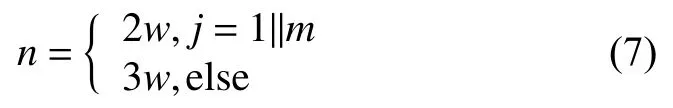
对Hj每行进行均值向量Uj与标准差向量Sj的求解计算，同时为满足光照不变性进行归一化处理，两者共同构成曲线矩形带Bj的描述符BDj可表示为

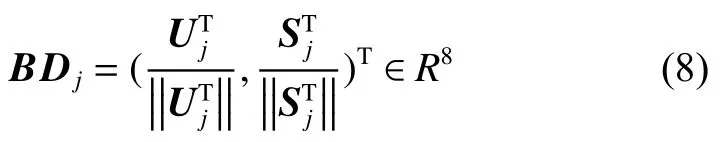
通过对所有矩形带描述符进行求解，获得曲线描述符CBD

根据最近邻距离比例原则，采用BF匹配算法匹配曲线描述符，曲线粗匹配结果如图3所示。

图3 曲线粗匹配Fig.3 Curves rough matching

2 曲线曲率匹配

2.1 三次B样条曲线拟合

基于曲线描述符的曲线匹配算法仅能对曲线粗略匹配，难以实现最相似部分匹配，影响后续导航精度。本文在此基础上加入基于曲率的曲线匹配算法，以实现对曲线的精准匹配。原始曲线为离散数据形式，为尽可能准确计算曲线曲率，需对曲线数据进行平滑拟合，同时削弱噪声的影响。

传统的贝塞尔曲线拟合方法仅需少量控制点即可生成复杂平滑曲线，控制简便且具有较强控制能力，但灵活性较差，难以修改局部特征，某一控制点发生改变对拟合曲线整体都有影响。针对贝塞尔算法的缺点，B样条拟合算法被提出，该算法逼近多边形特征精度更高，且具备局部修改性[21]，B样条算法曲线拟合表达式为

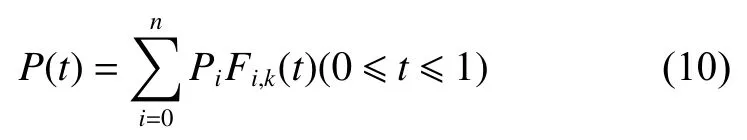
其中：n表示用来拟合曲线的点个数；Pi表示拟合曲线的离散点；Fi，k（t）表示的K阶基函数定义为

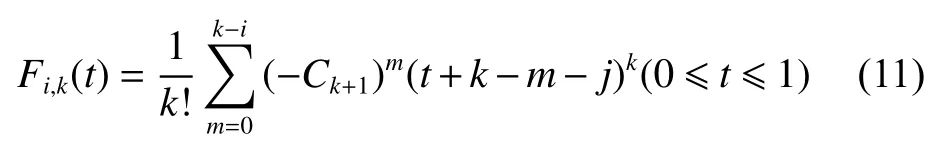
三次B样条曲线相比二次B样条曲线更加光滑，同时计算量在可接受范围。通过4个相邻离散点计算可得三次B样条曲线，对式（11）进行求解可得

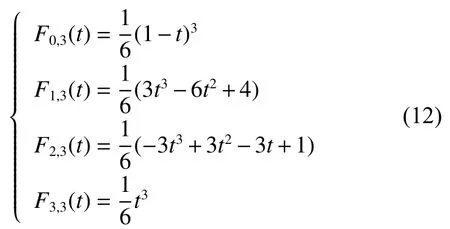
将式（12）代入式（10），得到三次B样条曲线表达式为

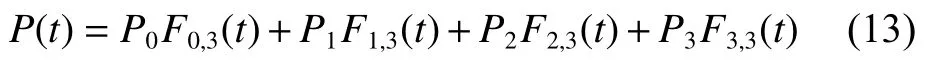
分别用2种算法拟合曲线，结果如图4所示。与3次B样条曲线拟合图4（b）相比，贝塞尔曲线拟合结果图4（a）整体趋势平滑，但对曲线细节表现力较差。基于曲率的曲线匹配算法是根据曲线弯曲程度进行匹配，对曲线细节拟合要求高，贝塞尔拟合曲线易造成误匹配，故B样条曲线拟合算法更适合。

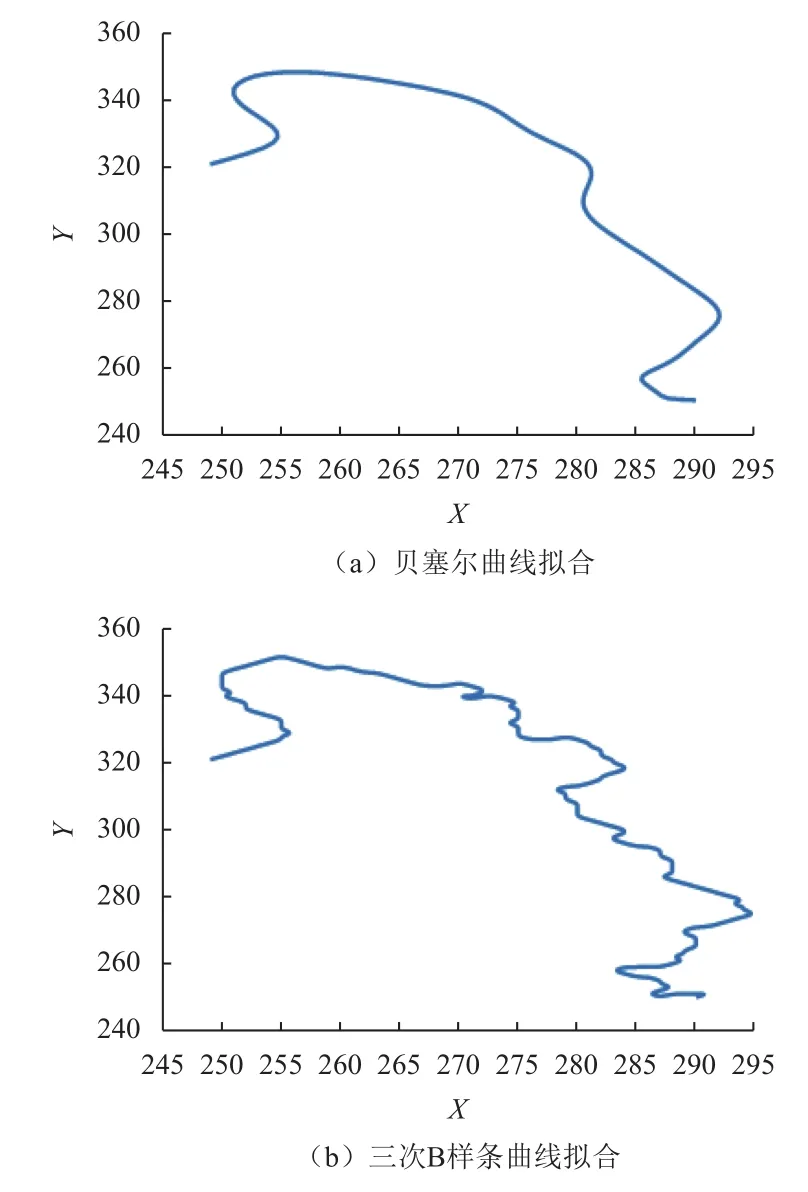
图4 曲线拟合结果Fig.4 Curve fitting results

2.2 尺度不变性曲率计算

对于图5中连续曲线，曲率表示为曲线弧切线转角与弧长之比

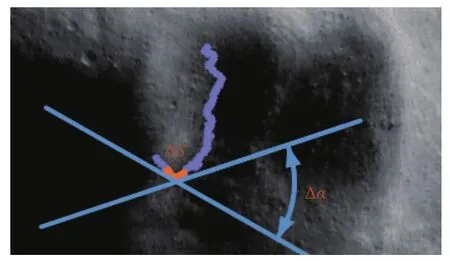
图5 连续曲线曲率Fig.5 Curvature of continuous curve

在曲线曲率基础上进行曲率积分计算，由于曲线中存在拐点，且有符号曲率积分非单调变化，导致同一积分数值可能对应多个曲率值，因此本文选择使用无符号曲率积分。给定弧长为l的曲线，曲线曲率绝对值积分为

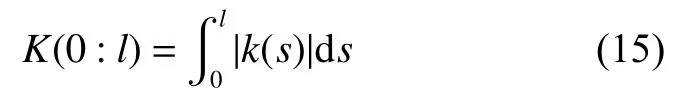
其中，K（0∶l）为曲率绝对值之和。将该曲线缩放a倍得到新曲线，其曲率绝对值之和为

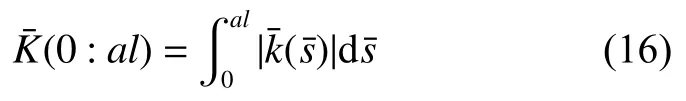
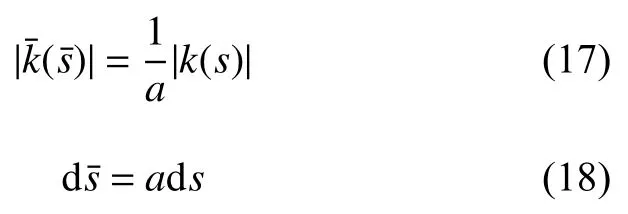
将式（17）与式（18）代入式（16）可得

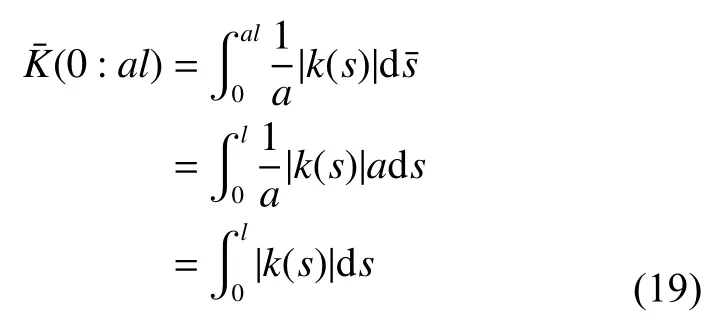
由式（19）可得曲率积分的尺度不变性，即如果两输入曲线具有相同的部分，则对曲线进行尺度变换，且两者尺度因子为m，则它们在弧长轴上（坐标轴横轴）的跨度之比也为m，且曲率积分（坐标轴纵轴）跨度相等[19]，如图6所示。

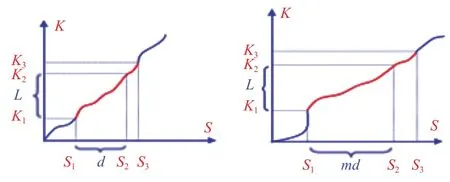
图6 曲率积分尺度不变性Fig.6 Scale invariance of curvature integral

利用曲率绝对值积分尺度不变性，以等曲率积分间隔对曲率进行采样，使采样后曲率具有尺度不变特性。对于尺度不同但存在相似部分的两条曲线，其曲率在经过采样处理后，其相同部分在横轴上跨越相同长度，两条曲线精准匹配问题转换为采样后两曲率曲线的精准匹配问题，简化匹配难度。

等积分间隔采样后，原曲率曲线变化剧烈处被拉长，而变化较平缓处被压缩。在设置采样间隔时，曲率积分间隔越小，曲线细节信息越准确，但同时会保留更多噪声，且计算量大；而间隔增大时会丢失部分数据信息，但可以削弱噪声影响并且减小计算量，如图7所示。经实验，积分间隔设置为5时，能保证数据精度同时加快运行速度。

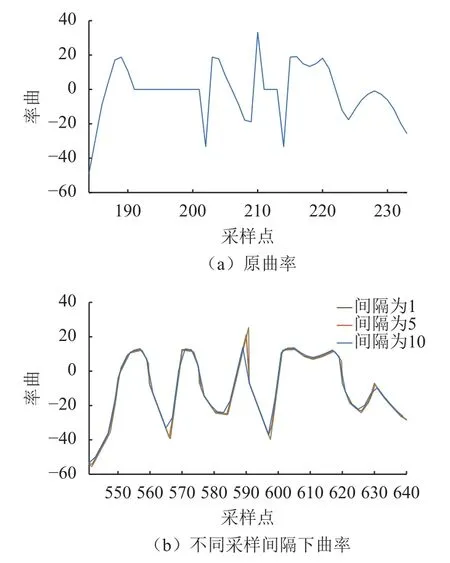
图7 原曲率与采样后曲率Fig.7 Original curvature and sampled curvature.

2.3 归一化互相关匹配

对于两条曲线采样后曲率匹配，采用归一化互相关算法进行相似度计算，计算公式为

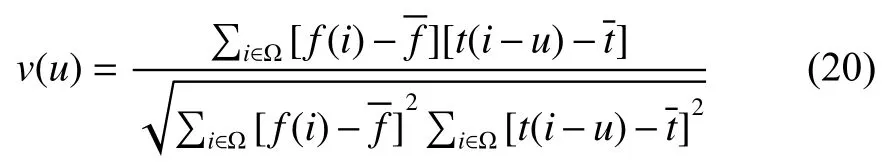
其中：f为较短曲线中的一部分，作为模板窗口沿着较长曲线滑动；u为两条曲线的偏移量；为模板内曲率均值；为滑动窗口在第二条曲线上曲率均值；v取值范围为[–1，1]，数值越大相似度越高。

为确定两曲线最相似部分，从较短曲线a中截取所有可能曲线段与另一曲线b进行曲率匹配。对于截取的第i条曲线段ci在曲线b上滑动匹配时，将互相关系数最大处（图8 P点）作为曲线段ci与曲线b的匹配度。曲线a上所有可能曲线段完成计算后，将匹配度最高曲线段作为两曲线最相似部分。

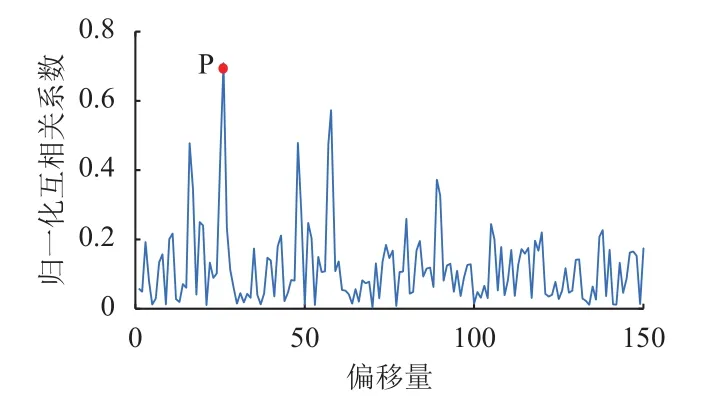
图8 曲线段匹配度Fig.8 Curve segment matching score

对于所有可能曲线段进行匹配时，曲线段越短通常相关系数越大，直接利用归一化互相关系数暴力匹配，计算量大且得到的大多是长度短、难以利用的曲线如图9所示。

图9 暴力匹配结果Fig.9 Brute force match results

为提高匹配效果并减小计算量采取以下策略。

1）设置曲线段长度与步长

精准匹配时对曲线a中所有曲线段进行互相关计算效率较低。经多次试验，设置步长与截取曲线长度为

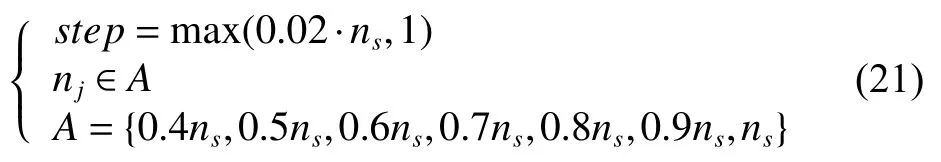
其中：step为步长；nj为截取曲线长度；A为截取曲线长度集合；ns为曲线a长度。

2）修改曲线段匹配度计算方式

考虑到曲线长度较长时，计算所得相关系数一般较低，为获得较长曲线匹配结果，计算匹配得分时加入曲线长度作为权重系数

其中：S为匹配结果最终得分；L为曲线段c的长度。

设曲线a长度为ns与b长度为nl，暴力匹配方法截取曲线长度nj∈[1,ns]，此时匹配计算复杂度

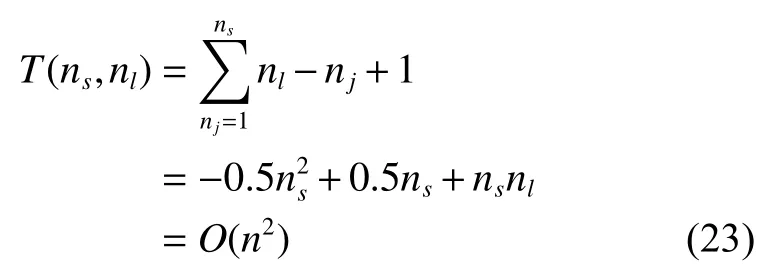
采取两策略后，匹配时间复杂度为

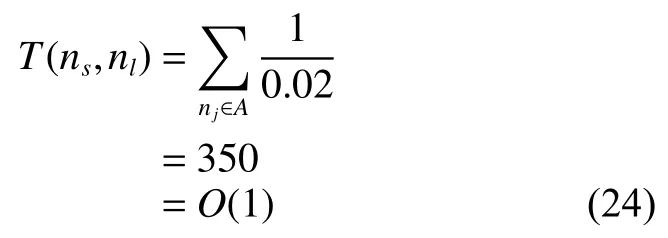
比较式（23）与式（24）可知，匹配时间复杂度最高次项由2次降为0次，计算量大幅减少，同时匹配效果得到提升如图10所示。

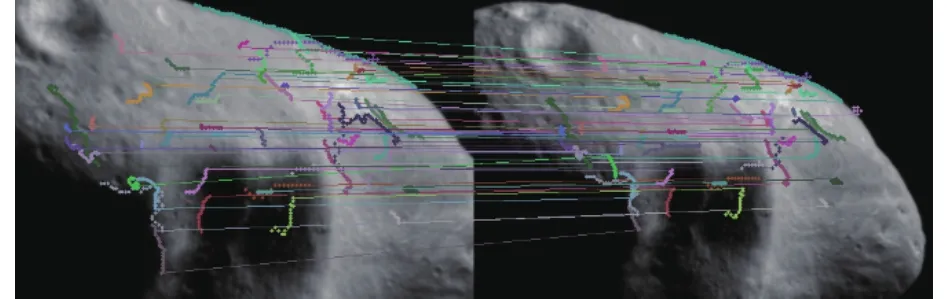
图10 采取策略后匹配结果Fig.10 The matching result after adopting strategies.

3 实验结果分析

对于本文提出的曲线精准匹配算法，从时间复杂度与精准匹配率两方面进行分析。

曲线匹配时间与硬件环境密切相关，因此使用算法执行所需要的计算工作量即时间复杂度来进行比较。基于描述符进行曲线匹配时，采用最近邻比率原则，需要找到最近邻和次近邻匹配项，设两匹配图像提取到的曲线数分别为n1与n2，则描述符匹配时间复杂度为

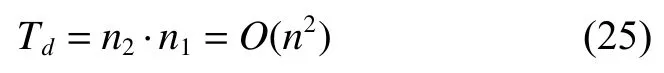
如2.3节中所述，在曲率匹配中一对曲线计算时间复杂度为O（1），则曲率匹配总体时间复杂度为

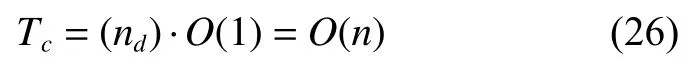
其中nd为基于描述符匹配得到的匹配曲线对数。

将描述符与曲率结合后算法时间复杂度为

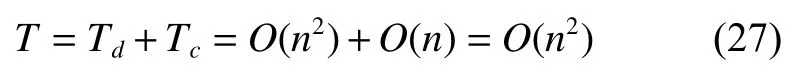
比较式（25）、式（26）、式（27）可得，在基于描述符匹配基础上，加入曲率匹配后时间复杂度仍然为O（n2）。本文提出曲线精准匹配算法与基于描述符的匹配算法相比，算法时间复杂度保持不变。

在精准匹配率方面，由于探测器下降阶段，图像纹理特征会发生缩放、旋转及光照变换，故分别在3种情况下进行实验。为评价不同变换下曲线精准匹配效果，对匹配曲线进行离散弗雷歇距离计算[22]。对于2条匹配曲线，根据两者长度之比设置采样间隔，得到长度相等的两曲线A、B。之后通过旋转、平移将两曲线端点重合如图11所示。

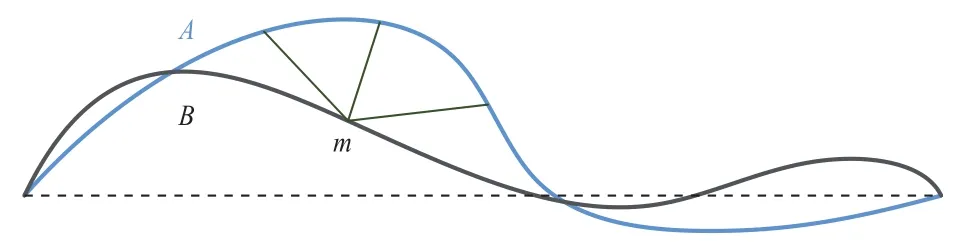
图11 弗雷歇距离计算Fig.11 Fréchet distance calculation.

计算两曲线弗雷歇距离时，对于曲线B上一点m，计算该点到曲线A上各点欧氏距离，将所有欧氏距离中最小值作为候选弗雷歇距离。对曲线B中各点完成计算后，将候选弗雷歇距离最大值作为曲线A与曲线B的弗雷歇距离。经实验，在评估时将弗雷歇距离小于5的结果作为精准匹配。

实验所用为从NASA官网得到的真实小天体图像。图12为尺度、旋转与光照变换下描述符匹配算法实验结果，表1为3种变换下相应精准匹配率。结合图12与表1可知，基于描述符匹配算法在尺度与旋转变换下精准匹配效果较差。

图12 不同变换下描述符匹配算法实验结果Fig.12 The experimental results of descriptor matching algorithm under different transformations

表1 不同变换下描述符匹配算法精准匹配率Table 1 The accurate matching rate of descriptor matching algorithm under different transformations

图13～15展示了尺度、旋转与光照变换下本文所述曲线精准匹配算法实验结果，表2为3种变换下相应精准匹配率。结合图13～15与表2可以看出，在尺度、旋转与光照变换下，本文描述的描述符与曲率相结合的曲线精准匹配算法可以达到84%以上精准匹配率。

表2 不同变换下精准匹配率Table 2 The accurate matching rate under different transformations

图13 尺度变换下实验结果Fig.13 The experiment results with scale variation

图14 旋转变换下实验结果Fig.14 Matching score with illumination variation

图15 光照亮度变换下实验结果Fig.15 The experiment results with illumination variation

4 结 论

针对曲线描述符难以精准匹配、曲率匹配仅能处理两条曲线的问题，本文提出一种将两者相结合的曲线精准匹配算法，主要包括曲线提取、描述符匹配与曲率匹配3部分。曲线提取部分根据Edge Drawing算法进行边缘曲线检测；描述符匹配部分对曲线及周围支撑区域信息进行描述，根据最近邻距离比率原则完成粗匹配；曲率匹配部分根据无符号曲率积分对曲率曲线重采样，并根据归一化互相关算法完成曲线精准匹配。实验结果表明，本文提出的算法可以达到84%以上的精准匹配率。