水闸渗流稳定及应力应变分析

刘文超 中国市政工程华北设计研究总院有限公司

1.工程概况

2.建立三维有限元模型

2.1 有限元模型的选取与坐标系建立

因本案例水闸采用的是分离式底板，且闸基土层的划分变化不是很大，故选用其中一个稳定断面来进行论述，选用三维非线性有限元模拟方法深入分析了中孔段。上游54m混凝土防渗铺盖下部至下游消力池前端为计算范畴，考虑到项目所在位置隶属于黄河冲积扇平原地貌单元，本研究在分析渗流稳定性的基础上，主要考察其稳定性性质，便于模拟。

2.2 材料参数及计算工况的选取

2.2.1 材料参数

本篇文章依据研究方向对坝体材料及坝基材料进行了材料性能指标计算解析。将4层闸基渗流模拟为非线性材料，依据有限元、分洪闸、地基材料的物理性能指标，将分洪闸闸门闸墩作为弹性材料处理。

2.2.2 荷载及计算工况

在计算中考虑的荷载为自重和水力荷载。其中水的容重取9.8KN/m3。其总体思想是首要进行渗流研究，并对渗流结果进行处理，以节点荷载加水压荷载的方式，在ADINA的稳定计算模块中对闸坝各节点进行应力、应变研究，地基部分自重造成的位移不计在内。在这一基础上，对本案例分洪闸门进行了渗流与稳定性计算，主要研究了分洪水位下的渗流与应力变形。最终，与力学法的计算结果进行了比较，其总体结果与力学法的计算结果相同。

2.3 三维模型网格的划分

根据对渗流边界条件的概念，判定本模型的地基底面和外围为不透水层。从应力应变分析边界条件概念的角度来分析，模型地基底面渗流约束为z=0，x=0或y=0，闸轴向y=0。该模型具有精度高、算法简单等优势。在有限元渗流分析中，构建优良的三维模型是核心，这也为后期边界条件和荷载的运用确立了基础，渗流应力及变形分析是水闸渗流稳定分析的基础。

3.闸室渗流稳定分析

3.1 段阻力系数计算

进、出口段：

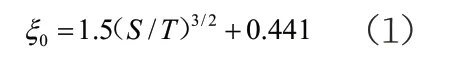
式中：ξ0指代阻力系数；S指代入土深度（m)；T为地基透水层深度（m)；

内部垂直段：

老马说：“这个就不好说了，根据各人的体质不同而定，人体一旦没了肾，体内不能维持体液电解质平衡和排泄代谢产物，而导致高血钾、代谢性酸中毒及急性尿毒症综合征，数小时至数天内都有可能死亡。”

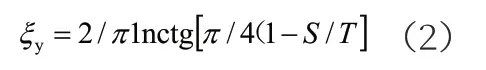
式中：ξy指代内部垂直段的阻力系数。

3.2 进出口段修正后的水头损失值计算

式中：h0′为进出口段修正后的水头损失值（m)；h0为进出口段水头损失值（m)；β′为阻力修正系数，当计算的β′＞1.0时，采用β′=1.0；S′为底板埋深与板桩入土深度之和（m)；T′为板桩另一侧地基透水层深度（m)。

3.3 渗透坡降计算

出口坡降计算公式：

水平坡降计算公式：

图1 分洪水位下最大主应力云图（单位：Pa）

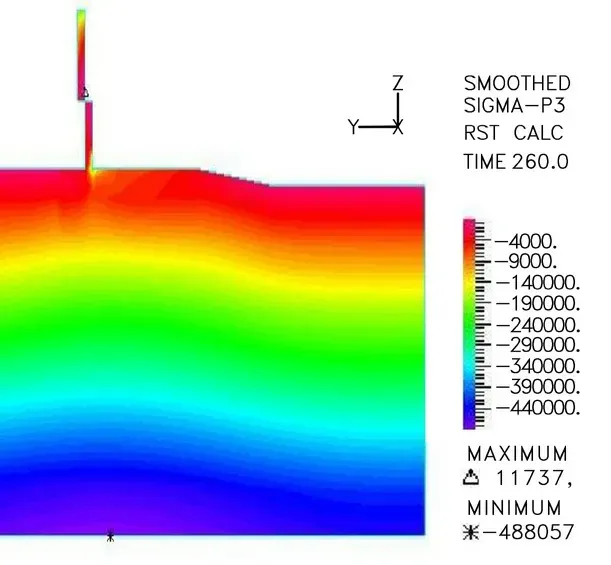
图2 分洪水位下最小主应力云图（单位：Pa）

图3 分洪水位下 Z 方向主应力云图（单位：Pa）

式中：J为出口段渗流坡降值；Jx为水平段渗流坡降值；ΔH为水平段水头损失值（m)。

4.水闸的应力变形及成果分析

4.1 水闸的应力变形分析

该方案的应力应变分析，是在渗流稳定性分析的基础上，需在节点处增加渗流力且在每一水位处增加水荷载，再对闸室P1中段纵断面进行应力应变分析。

4.2 水闸应力变形成果分析

（1）第一主应力。分洪水位只相差0.5m就可以到达闸门顶的现有高程。当水位较低时，闸门P1段的上游位置最高值拉应力达到了0.16MPa；闸室地基底部出现了最大压应力。在Y方向的应力分布中可以看出其闸门附近存在较大的拉压应力，而z方向的压应力分布呈越往下越大的趋势。

（2）第三主应力。从图中可以看出，第三主应力与第一主应力分布上面较为相似，地基底部同样分布最大压应力，达到了0.49 MPa。

（3）垂直应力。竖直方向的应力主要分布在闸门和底板相衔接的范围内，最大拉应力为0.11 MPa；地基最底层的压应力与第三主应力相同。

（4）Y向位移。当水位较低时，向Y方向的渗流发生移位较明显，最大移位值0.12mm，分布于闸门背水面范围内。此外应力变形分析中还发现闸门底板接触部分存在不同程度的位移情况，位移走向趋势与顺水流方向一致。

（5）Z方向位移。垂直向上的最大位移数值为0.01 mm，主要分布于闸门中下部；垂直向下的最大位移数值为0.08 mm，分布位置为闸室底板和基础的交叉处。应力应变结果如表1所示。

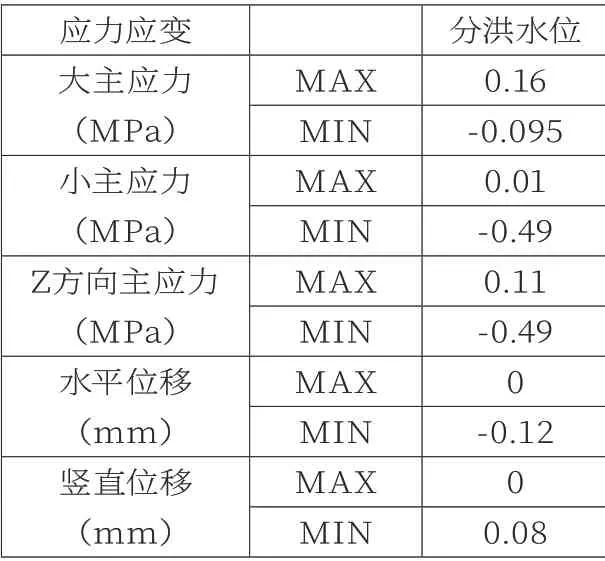
表1 应力应变结果

5.结束语

鉴于水闸形式的多样化，从有限元建模到模拟计算都是一个复杂的过程。文中的研究受到时间和研究条件的局限，所做工作十分有限，有众多问题仍待更进一步探究。本文通过工程实例，对某闸门在分洪水位下的位移、应力分布及其变化特征进行了讨论，并对位移、应力的变化趋势进行了分析。有限元分析表明，闸室P1段纵断面底板与胸墙底部的连接处存在较大的拉压应力。渗流力在Y方向发生位移对水闸的稳定性造成的影响最大，而上游水位的变化对其干扰并不大。通过上游54m的铺盖能够满足本案例水闸渗流稳定的要求，并且其渗透坡度经分析表明较为合理。因此综合本案例的实际情况与笔者本人施工经验，建议采用上游防渗铺盖的方式，再加上与灌注桩相结合的方案，可以满足该水闸渗流稳定，又使应力应变满足要求。