社会网络问题中的算法

人和人之间的关系，可以看成是一个网络，可以用图或有向图来描述，或者说用它们来建模。在本栏目第2期讨论一笔画问题时我们接触过图，在第4期谈连通问题时针对的也是图，而在第13期讨论网络最大流问题时采用的模型则是有向图。第21期谈选举，也用到了有向图。图和有向图是用算法求解问题中十分常见的一类模型。

取决于所考虑的人群范围和关系的定义，社会网络，有时也称社交网络，可以多种多样。最熟悉的，是现实生活中的“熟人”关系，见面相互都能叫得上名字，用图来描述就很合适，如图1（a）所示。而微博博主之间的“粉丝关系”，不一定是互相的，用图来表示就不合适了，需要用有向图，如图1（b）所示。箭头方向就表达了粉丝关系的单向性。如果两个人互粉，如节点2和节点5，那么他们之间就有两条不同方向的边。

社会网络分析有许多现实的意义。例如，在新冠肺炎疫情期间，发现一个病例，要确定他有哪些“密接者”，就涉及社会网络分析。那种社会网络，其中的边具有时间特性（只是在某个时间段存在），也称作“接触网络”。现在一些城市要求市民在一些场所通过扫描特定的二维码“打卡”，其意义之一就是为了在发现病例的时候，能够迅速构建与他相关的接触网络。

本文介绍社会网络分析中的两个基础算法，让读者从中了解社会网络分析的一种主要计算模式——矩阵运算①。这类算法，从算法逻辑的角度来说，会显得比本专栏前面介绍过的那些算法简单许多，它们的引人入胜之处在于其结果体现了某些社会现实意义。在讨论中，我们总假定网络结构是已经给定的有向图，而且采用的是邻接矩阵表示。在本栏目第4期讨论图的连通问题时，我们用过图的邻接矩阵表示。不过那里仅涉及无向图，邻接矩阵是对称的;本文则主要关注有向图，邻接矩阵一般不对称。例如，图2（a）就是前面图1（b）中有向图的邻接矩阵表示，其中行和列的编号对应图中的节点，即第i行第j列的值aij=1，当且仅当有一条从节点i指向节点j的边。有时候，如果需要表示一个节点指向自己的情形，就会有aii=1。

对矩阵概念陌生但对编程比较熟悉的读者，不妨就想像程序语言中的“二维数组”。在Python中可用二维列表或者numpy中的数组直接体现，如图2（a）中的矩阵用二维列表给出就是：

A=[[0，0，1，0，0，0]，

[1，0，1，1，1，0]，

[0，0，0，0，0，0]，

[1，0，0，0，1，0]，

[0，1，1，0，0，1]，

[0，0，1，0，0，0]]

用A[i][j]訪问它的第i行第j列元素。有时候，为方便起见，也用矩阵（数组）的第i个行向量和第j个列向量来分别指代A[i][j]，j=1，2，…，n和A[i][j]，i=1，2，…，n。注意，它们分别都包含n个元素，视觉形象上对应数组的行和列。

我们要讨论的两个算法，其社会现实意义分别与社会网络中人们的“发言权”和“影响力”有关。为了体会这些说法的现实含义，不妨考虑下面这样一种情境。

设想在某中学的一个班里，学生们相处久了相互已经比较熟悉。现在要讨论某个话题，如生物多样性，或者校门口那一棵大槐树的高度。教师让每个学生分别填写表1，写出自己的姓名和2～5个认为对该话题比较有发言权的同学的姓名。

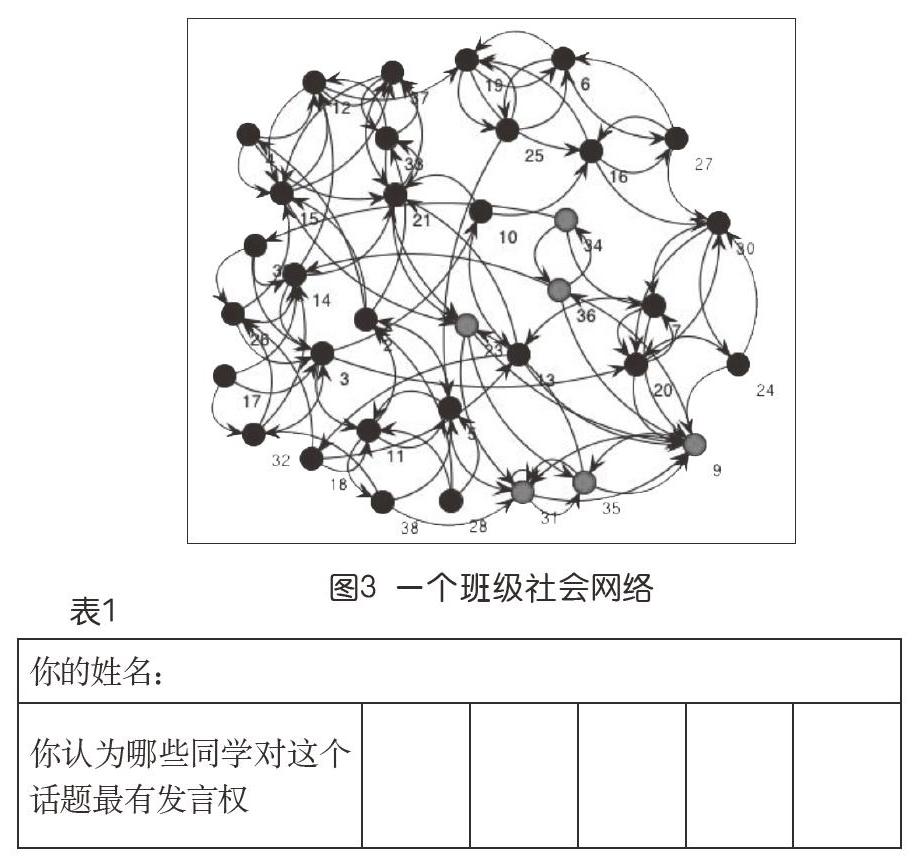
教师收上来这些纸条，你马上能意识到，她有了一个社会网络的数据，而且其中表达的关系是有方向性的：每个学生是其中一个节点，如果学生i在他的表中提到了学生j的名字，那么网络中就有一条从i指向j的边。例如，图3就是一次实际填报数据给出的结果。我们看到每个节点发出有若干指向其他节点的边（称为出向边），同时作为结果，每个节点也“收到了”若干来自其他节点的边。此处重点是，这种“入向边的条数（称为“入度”），不同节点很可能是不同的，反映了一个学生被其他学生“认可”的情况。

一般来说，针对一个话题，每个学生都会有自己的观点，有的坚实，有的飘忽，姑且称其为不同程度的“发言权”。而这种程度是被其他同学看在眼里，表达在上述表格中的。显然，这种发言权意味着某种价值，有高低。我们来介绍一种评估这种价值的计算方法。

按照填表时给学生的背景意义，我们可以理解，如果节点i的入度大于节点j的入度，大致可以说明更多的人认为i比j对当下话题更有发言权。也就是说，节点的入度可以是发言权高低的一种指示器。不过我们还想更进一步，认为一个人的发言权不光取决于有多少人认为他有发言权，还取决于认为他有发言权的人有多大的发言权。同时，若某人认可的人较多，他的分量体现在一个人身上应该较少。直觉上，这是有道理的。利用一些合理的直觉（尽管不一定能证明总是对的），形成启发式来指导计算，是利用计算机求解问题的一种基本策略。在本栏目前面的文章中我们已经看到过不少例子。在这种思想下，接着就要考虑两点，一是将启发式变成算法，二是在应用实践中检验。

下面就是解决这个问题的著名的PageRank算法，它通过迭代同时更新每个节点的值，直到收敛误差满足要求或达到某个预设的迭代次数。算法要点是：在迭代的每一轮，让每个节点将自己的当前值均分给出向邻居节点，同时将从入向邻居节点收到的当前值加和作为自己下一轮的当前值。图4给出一个示意。关注左边图中的节点v，它有3个入向邻居，每个有不同的出度。右边则是按照上述算法思想对v进行更新的公式。

不难想到，基于有向图中的连接关系，对每一个节点都可以写出一个类似但不同的公式来。假设有n个节点，通常令每个节点的初值为1/n，按照公式进行迭代，就是PageRank计算的过程。在我们前面设置的背景问题下，这也就是学生们对某一个问题的“发言权”的计算过程了。

不过，上面只是阐述了“算法思想”。落实到明晰的算法描述还需要做些整理。关键在于“按不同的公式同时更新每个节点的值”具体怎么实施。这里首先要解决的是不同公式的统一表达问题。

令v=（v1，v2，…，vn）为拟求的网络节点PageRank值的向量，其中每个vi对应一个节点。

为了体现算法思想中的“将当前值均分给出向邻居”，我们在网络图的邻接矩阵（A）基础上，用节点的出度除每一行，得到矩阵A'。图2（b）就是对应图2（a）的例子。其中第3行有些特别，多出了一个“1”，待下面解释。现在重要的是可以看到，向量v左乘A'，即v←vA'，恰好就是按公式对所有节点的同时更新。为什么呢？请读者思考体会。

一般地，所谓一个n元行向量v=（v1，v2，…，vn）左乘一个nxn矩阵M，其中元素用mij表示，就是用v和M的每个列向量分别相乘（内积），得到一个结果向量w= （w1， w2，…，wn）。其数学关系就是：

对应到程序中的数组操作表达如下：

w=[0]*n

for i in range（n）：

for j in range（n）：

w[i]=w[i]+v[j]*M[j][i]

注意到我们现在用的矩阵M是A'，如果它的第i列中的第j个元素非0，意味着在网络中节点j指向i，且该元素值是节点j的出度的倒数，于是v[j]*M[j][i]正好就是节点j均分给i的PageRank值。都加起来，就正好是按照算法思想给出的节点i的更新值。

于是，我们可以写出算法了。

● PageRank基本更新算法（如下页表2）

表2中，第4步的具体实现可参考前面的代码段。这里有一个重要问题提请读者注意，如果网络中有节点的出度为0，会出现什么情况？在我们谈到的“发言权问题”背景下不会有这样的问题（因为假设每个学生都按要求提交了一张表），但一般情况下难免，如图1（b）中的节点3，就只有入边没有出边。一旦有这种情况，算法第1步就会遇到除数为0的困难，在这种情况下，通常的处理方法是令该节点指向自己（图2（b）矩阵中的A'[3][3]=1就是这么来的）。

不过这还没有完，还有一个更严重的潜在问题。想想上述PageRank更新规则的含义，如果某节点没有指向其他节点的边，它就会表现得很“自私”——不断从其他节点吸纳价值，全部累积在自己身上，从而让算法失去意义。为此，PageRank设计者在算法中增加了一个“同比缩减+等量补偿”规则，也就让它真正实用了。有进一步兴趣的读者可参阅其他资料，在此不赘述。

另外，值得一提的是迭代过程的收敛问题。理论上，包含“同比缩减+等量补偿”规则的算法总是可以收敛的，但需要无穷时间，因而在实际应用中需要有结束控制。上面的算法描述是依靠预先设定的一个迭代次数，实际中也可以通过判断相继两次迭代结果之间的误差来控制。

下面来看社会网络分析中的另一个算法。我们还是以前面的班级网络为情境，学生们给出了他们认为谁更有发言权的数据。反过来说，每一个学生对当下话题的观点就会有一定的“影响力”。如果网络中有一条i指向j的边，那么可以想象j的观点就会对i有影响。我们来考虑观点在社会网络中的传播问题。

在有向图上的观点传播，一个简单模型（DeGroot）是这样的：假设每个节点i有一个代表其观点的初值vi，构成向量v=（v1，v2，…，vn），传播过程以迭代方式进行，每一轮每个节点同时用对它有影响的节点的均值更新自己。就好像在对一些事情的态度上你会综合考虑朋友们的态度，不愿意走极端。

最后会怎么样？最后所有节点会收敛到同一个值（记为c）！这似乎是在说在一个封闭世界中，一群人互动，长此以往，大家的观念会趋同。下面是算得这个共识值的算法。假设我们还是用前面算PageRank时的初始矩阵A和A'，其中“有影响”的含义如上所述，即节点受其出向邻居的影响。

此时我们特别注意到，由于A'是在A的基础上通过每行除以节点出度而得，为了符合上面影响力传播模型的描述，矩阵向量运算时迭代向量应该出现在矩阵的右边（用矩阵的行向量和它相乘），从而体现了“对其有影响的节点的均值”的要求。这是和PageRank算法的一个本质不同。读者可以尝试写出和前面类似的数学关系和数组操作代码段。下面是算法描述。

● DeGroot共识算法（如表3）

算法尽管输出的还是一个向量，但其中的元素趋同，无论初值如何。

那影响力是怎么回事？不是说不同的人有不同的影响力吗？而且通过前面的讨论，“发言权”（PageRank值）较高似乎应该对应影响力较大才是。

细心的读者此时也许看出点门道来了。此处以PageRank概念为表征的“发言权”的确对共识的形成有着一种精妙的影响，那就是：设v=（v1，v2，…，vn）为初始观点向量，c是在DeGroot算法下得到的共识值，记p =（p1，p2，…，pn）为在PageRank算法下得到的结果，则：

这个结果的严格证明需要些线性代数知识，此处略过。它表明，一个人的PageRank值越高，他的观点在形成群体共识中的作用就越大。PageRank扮演了对其观点“加权”的角色。这也意味着，在社会网络中，一个人的“发言权”，正好也就是它的“影响力”。当然，这种“精确的结论”只是在上述PageRank和DeGroot模型意义下才成立，现实情况自然要复杂多了。

至此，我们完成了本文所有技术性讨论。此时值得回头再看看PageRank和DeGroot算法。除了要用到一点非常基础的矩阵向量运算外，算法逻辑本身十分浅显易懂，也就是说，按照它们写出程序来会很简单。不过，这种算法描述的简单不意味着计算复杂性低，事实上，从前面给出的数组操作代码段可以看到是一个二重循环，再加上迭代次数控制，就是一个三重循环，对于较大n，就会比较耗时。

通过这两个例子，读者也许能体会用矩阵表示图结构对于许多算法描述的便利，要點是认识到矩阵向量运算和图中节点值的更新规则之间的对应关系。类似的问题还有很多，如本栏目第21期讨论的选举问题，也是涉及在初始向量元素是全1的输入下，按照“竞赛图”（完全有向图）来迭代更新每个选手的得分，最后排出一个高低来。显然，竞赛图可以用矩阵表示。这里的问题是，如何用矩阵向量计算来描述该算法呢？特别地，参照本文前面的算法，这里需要对矩阵做什么预处理吗？如果要做矩阵和向量相乘，向量该放在左边还是右边？请有兴趣的读者自行思考回答。

从2019年6月开始，本栏目规划的24篇与算法相关的小文章到这一期就都完成了。这些文章的内容，不一定都适合直接在中小学计算机课上教学生，但我们相信它们所体现的内容范畴和认知要求应当在教师的素养之中，同时也认为如果没有整块的时间系统学习算法知识，这24篇相对独立的短文当适合作为“碎片化学习”的素材。目前，我们中小学计算机课程正在经历一次重大变革，算法无疑是计算机课程的核心。数理化在我国中小学能教得很好，算法也应该能教好。

释：①尽管中学数学课没有包含矩阵方面的内容，但我们认为在学习信息技术课程（尤其是数据结构与算法）的时候，结合程序中数组的概念，简单介绍一点矩阵知识和基本运算，既有很大的益处，也为中学生的认知能力所及。

参考文献：

[1]（美）大卫·伊斯利.网络、群体与市场[M].李晓明，王卫红，杨韫丽，译.北京：清华大学出版社，2011，10.（关于PageRank的介绍出现在第14章）

[2]Matthew O. Jackson.The Human Networks[M].New York：Pantheon Books，2019.（162-170页是DeGroot模型的通俗介绍）

[3]李晓明.连通还是不连通[J].中小学教材教学，2019（09）：75-80.

注：作者系北京大学计算机系原系主任。