黄渤海海域波浪时空变化特征分析

邱文博,李冠宇,徐俊臣,胡轶群,王亚丁,石洪源

(1.国家海洋技术中心,天津 300111; 2.鲁东大学土木工程学院,烟台 264025)

黄渤海的波浪具有明显的季节性。针对黄渤海地区的波浪特征分析,国内外学者已经做了很多相关方面的研究[1-4]。其中,有一些研究是利用实测资料开展,因实测资料具有时空限制性和区域性,无法满足在长时间跨度、宽领域尺度情况下对波浪分布特征的研究。随着卫星遥感的发展,利用卫星开展波浪特征的研究也逐步展开,例如齐义泉等[5]为分析黄海中部的风、浪基本统计特征及季节分布特征,利用了卫星高度计遥感资料; 陈红霞等[6]为分析中国近海随时间变化和季节变化的特点,利用了TOPEX卫星高度计资料。王广运等[7]根据T/P卫星高度计资料和 ESR-1卫星散射计资料,推算出中国两个海域多年一遇的波高极值。虽然卫星遥感技术具有观测范围大、观测时间长的特点,但是其也存在一定的局限性,例如在极端天气情况下,遥感数据会出现较大误差,同时卫星轨道具有周期性,其周期10～35 d不等,不能做到数据的实时覆盖性[8]。随着数值模式的发展成熟,目前第三代数值模型广泛被应用于海浪相关研究工作中,例如谢冬梅等[9]利用WAMC4数值模型对东中国海1950年—2009年的波浪进行后报模拟,并以模拟数据为基础展开了对该海域波浪时空分布特征的研究。陈国光[10]通过SWAN数值模型,对黄海海域波浪有效波高的季节变化特征展开了研究。

由此可以看出,前人已展开了较多关于黄渤海波浪特征相关方面的研究,开展这些研究的数据主要以实测数据、数值模拟或卫星资料为主。本文采用European Centre for Medium-Range Weather Forecasting (ECMWF)第五代再分析数据集(ECMWF Reanalysis v5,ERA5)的高时空分辨率的波浪场(0.125°×0.125°),针对黄渤海区域近 20 a(2000—2019年)的波浪特征进行分析,包括四季有效波高(Significant wave height,Hs)和平均周期(Mean period,T)的分布规律,然后对波高进行 EOF分解,最后选取 4个代表点给出其波浪玫瑰图。上述工作是前人比较少涉及的,本研究主要分析了黄渤海地区波浪在时间和空间的分布及其变化特征,所得结论对海洋水文保障、海洋工程建设及运营等具有重要的科学参考价值。

1 数据资料

1.1 数据来源

ECMWF在全球再分析数据集中,是比较知名的。其中它的 ERA5数据集使用了专为再分析而开发的综合预报系统(IFS cycle 41r2)[11],相比于ERAInterim[12],数据准确性得到了显著改善[13-14]。许多研究人员将其用于大气和海洋研究,例如Naseef等[15-16]利用39 a ERA5数据(1979—2017年)分别研究了台风对印度洋海域百年一遇波浪极值的影响以及该区域波浪及气候特征的变化趋势。Bruno等[17]利用实测资料评估了ERA5数据在涌浪占主导海域的适用性,结果证明 ERA5数据具有良好的适用性。本文利用黄海海域2个实测站点浮标观测数据(2011年1月1日—2017年12月31日)对ERA5的准确性进行验证,观测站位见图1。

图1 研究区域、代表点(黑色圆圈)和验证点(黑色三角)位置 (审图号: GS(2020)4631号)Fig.1 Research area and locations of the representative and validation points (On drawing No.GS(2020)4631)

实测数据与ERA5数据对比结果见图2和表1。经计算统计Y1和Y2实测数据与ERA5数据的相关系数分别为0.91和0.97。因此,本文认为ERA5再分析数据在我国海域具有一定的适用性,可用于本文相关研究。

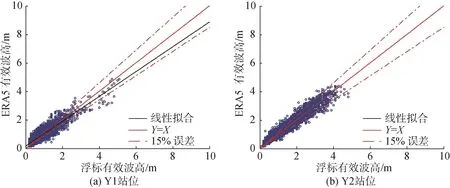
图2 实测站点与ERA5数据对比Fig.2 Comparison of measured site and the ERA5 data

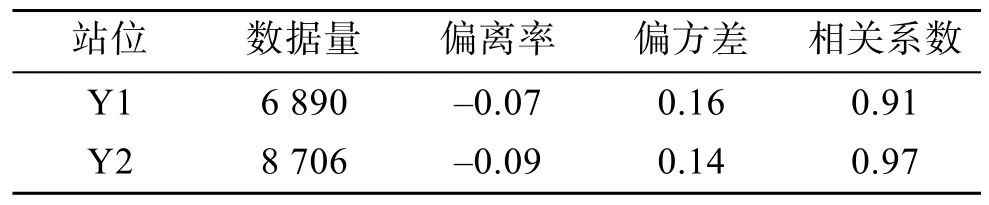
表1 实测站点和ERA5数据对比统计结果Tab.1 Statistical results between the measured site and the ERA5 data

1.2 研究范围

空间范围: 本文选取渤海及黄海大部分区域(117°～125°E,30°～41°N)作为研究对象(见图1),空间分辨率为0.125°。为便于直观分析黄渤海区域波浪特征,分别在渤海和黄海各选择两个代表点,命名为A(119.75°E,38°N)、B(120.25°E,39.5°N) 、C(123°E,38.5°N)和D(123°E,35°N)。

时间范围: 本文计算时间为 2001—2019年,共20 a,时间分辨率为1 h。

2 黄渤海波浪特征分析

2.1 波高分布季节特征

黄渤海区域受季风影响明显,其风场的基本特征为冬、夏季风盛行,冬季风持续时间为10月至次年3月,期间由于蒙古高压控住南海北部,导致东北风盛行。夏季风持续时间为5月至9月中旬,期间由于印度低压和太平洋副热带高压的影响,导致偏南风盛行。

本文分别对黄渤海春(3—5月)、夏(6—8月)、秋(9—11月)和冬(12月—次年2月)的有效波高Hs展开分析,其在黄渤海海域的年均分布见图3。

图3可知,渤海区域整体有效波高较小,呈现周边小,中间大的特点,这与水深有密切关系。其中,渤海中部年均有效波高可达0.5 m以上,周边海域年均有效波高仅冬季可达 0.5 m左右,其余季节不足0.5 m; 黄海海域有效波高呈现由南向北降低的趋势,其中最大值出现在黄海南部的长江口外海域; 北黄海海域冬季年均有效波高最高可达1.2 m,其余季节均在1 m以下。

图3 研究区域有效波高的季节年均值(单位: m)Fig.3 Seasonal annual mean Hs in the research area (Unit: m)

2.2 周期分布季节特征

平均周期T的季节分布类似于有效波高Hs的季节均值分布(图4)。渤海中间海域平均周期T的季节均值较大,四周浅水区域平均周期T的季节均值较小,仅秋冬季平均周期T的季节均值存在大于4 s的区域,春夏季平均周期T的季节均值均不足4 s。平均周期T的季节均值在黄海海域也呈现出由南向北递减的趋势,其中长江口外海区域秋冬季平均周期T的季节均值可达6 s; 北黄海海域全年T的季节均值均在5 s以下。

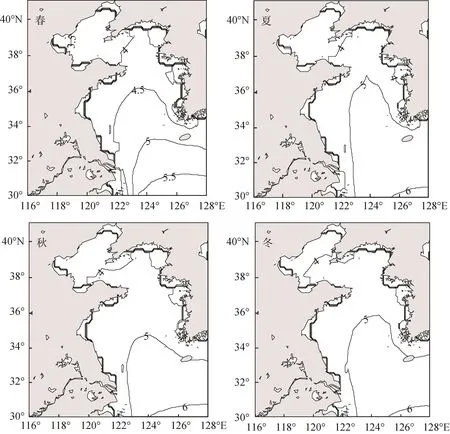
图4 研究区域平均周期的季节年均值(单位: s)Fig.4 Seasonal annual mean T in the research area (Unit: s)

2.3 有效波高的EOF分解

经验正交函数(EOF)方法现已经成为大气、海洋及其他地球物理科学中数据分析的有利工具。该方法最早在1902年由统计学家 Pearson[18]提出,该方法通过将场的时间序列作为分析对象,将原始场分解成两个不同的函数,分别为只依赖空间的函数和只依赖时间的函数,然后将两个函数相乘,以此进行分析。但在20世纪80年代以前,由于实测数据稀缺,很难进行大范围领域和长时间宽度的 EOF分析。随着卫星遥感技术的广泛应用和数值模拟技术的完善,EOF法逐渐应用于海洋领域的研究。例如韩树宗等[19]利用EOF分解对南海海域32 a的波浪场进行了研究。

本文利用月平均处理的方法,将从 ERA5上获取的2000—2019年20 a的黄渤海浪场数据进行处理,得到了 240 m的逐月有效波高均值数据,然后求得240 m的距平场之后对其进行EOF分析。值得注意的是,本分析中的距平不能采用240 m均值的距平,这会造成第一模态对方差的贡献率很大,应按照月份求得12 m的均值,再得到20 a中各月距平。

有效波高距平场EOF分析的前5个模态的方差贡献率见表2。其累积方差贡献率达到了97.42%,其中前 3个模态的方差贡献率之和达到 93.91%,因此本文对前3个模态进行了详细分析。

表2 模态的方差贡献率(前5个)Tab.2 Variance contribution rate of modes (Top 5)

第一模态的方差贡献率为 74.74%。南黄海区域为其空间分布的大值区域,大致呈 NW-SE走向(图5a),大值区域位于长江口至济州岛连线的中间区域,这里变化较大的原因主要是台风引起,造成有效波高值起伏较大。此外,第一空间模态的有效波高距平场在研究地区显示为正值,表明研究地区的有效波高的总体变化趋势是同增或同减,表明了该研究区域波浪变化的一致性。第一模态的时间序列以1年为单位呈现周期变化,从图6可知,冬季的时间序列呈现出＞0的形态,表明黄渤海的有效波高在冬季时增大的; 春季的时间序列大部分呈现出＜0的形态,表明黄渤海的有效波高在春季是减小的。此模态的物理意义是黄渤海波浪在风场的作用下,一年内变化的主要趋势与形式和黄渤海区域的季风密切相关。

第二模态的方差贡献率为 14.03%,其空间分布上在34°N附近有一条大致呈E-W方向的分界线,以南为负值,以北为正值(图5b),表明两个分区的波高变化呈现出相反的关系,即34°N以北海域波高变化幅度大,以南海域波高变化幅度小。据推测,此模态的物理意义可能代表有效波高受季风周期性影响的变化。时间系数在冬季呈现负值,表明在冬季风增强的影响下,34°N以北海域的波浪呈现增大的趋势,34°N以南海域有效波高变化除了受冬季风影响之外,可能还受涌浪分布等影响; 夏季的时候时间系数为正,这个趋势刚好相反(图6)。

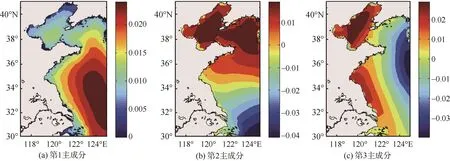
图5 有效波高距平场模态空间分布Fig.5 Modal spatial distributions of the significant wave height anomaly field

图6 有效波高距平场模态时间系数(前3个)Fig.6 Modal time coefficients of significant wave height anomaly field (Top 3)

第三模态的方差贡献率为 5.14%,该模态的空间分布情况,从图5可知,黄海深水区为其小值区域,而渤海以及黄海沿岸区域为其大值区域。从图6可知,第三模态的时间系数呈现出以年为周期的变化趋势,对物理意义进行分析推断可知,此模态的等值线趋势是沿海岸或海底地形进行分布的,这可能表示地形对有效波高的某种影响。但该模态仅解释了 5.14%的方差贡献率,所以难以排除是一些较小的物理过程对波浪变化的影响。

2.4 特征点波浪特征

以A—D为代表点,本文对20 a的黄渤海区域波浪特征展开具体分析,其中4个点的波浪玫瑰图见图7。

图7 代表点的波浪玫瑰图(2000—2019年)Fig.7 Wave rose in representative points (2000—2019)

A和B分别位于渤海海域的南部和北部,代表了渤海不同海区的波浪特征。由图5可知A点波浪以NNE向为主,其频率为17.6%,其次为S向,频率为14.8%,有效波高2.5 m以上的大浪主要集中在NNE和 NE向。B点波浪主浪向为 NE向,其频率可达19.0%,次浪向为S和SSW向,二者相差不多,分别为13.5%和13.2%,有效波高2.5 m以上的大浪仅NE向存在,相比A点波浪而言,这主要与冬季北风风区长度有关,因此A点有效波高最大值高于B点。

C点和D点分别位于北黄海和南黄海,其中C点波浪主浪向为 S向,次浪向为 SSE向,分别为16.7%和12.6%。有效波高大于2.5 m的大浪分布在N、NWW和SE向。D点波浪的主浪向为SSE向,频率为14.3%,次浪向为N向,频率为13.0%; 有效波高大于2.5 m的大浪分布N、SSE和SE向。

与前人研究成果对比,本文对20 a波浪特征展开分析,这在之前的研究中很少有人提及。根据特征点统计结果,可以得到黄渤海海域主浪向、大浪分布等特征,为海洋工程建设、海洋资源开发等提供一定参考。

3 总结

前人研究中,黄渤海海浪特征多集中在时空领域研究,例如波高周期的年均、季节时空变化等,本文采用 ECMWF的ERA5再分析波浪数据,首次利用EOF分解的方法,对黄渤海近20 a的波浪展开主成分分析,探讨黄渤海海浪特征表征的主次要因素,从而为黄渤海海浪的特征分析、变化预测等提供一种新思路。同时,利用该数据集,选取 4个代表点,获得波浪统计结果,主要结论如下:

1) 黄渤海海区波浪具有明显的季节性,冬季有效波高均值大于其他季节,这与冬季风有直接联系。其中,渤海区域有效波高呈现出周边小,中间大的特点,这与渤海的水深有一定联系; 黄海海域有效波高Hs呈现由南向北降低的趋势,最大值出现在长江口外海域,冬季均值可达1.7 m。

2) 黄渤海区域黄渤海平均周期T的季节分布类似于有效波高的季节均值分布。渤海仅秋冬季T的均值存在大于4 s的区域; 黄海海域T的季节分布也呈现由南向北递减的趋势,其中长江口外海区域秋冬季T的季节均值可达6 s,北黄海海区全年均值不足 5 s。

3) 有效波高距平场EOF分解结果显示,第一模态的方差贡献率为 74.74%,反映了波浪变化的主要形态,其时间系数为正,表明有效波高的变化趋势具有一致性,整个区域大致上是同增大或同减小;第二模态的方差贡献率为 14.03%,反映了季风的季节转换对有效波高的影响; 第三模态的方差贡献率为 5.14%,其空间模态的等值线分布有和岸线或地形有贴近的趋势,代表的可能是地形的变化对有效波高变化的影响。值得注意的是,本研究中对不同模态代表的意义可能并不具有空间的普适性,其具体含义待进一步研究。

4) 4个代表点显示,整个渤海地区的常浪向为NNE-NE,强浪向以NE和NNE为主; 黄海海域的常浪向为SSE-SE向,强浪向以N和SSE为主。这主要是由于冬季风的风速大且持续时间长造成的。 该统计结果,可为海洋工程建设提供一定参考。