基于最紧密堆积理论的超高性能混凝土配比设计

叶显 纪宪坤 吴文选 李磊 邹伟

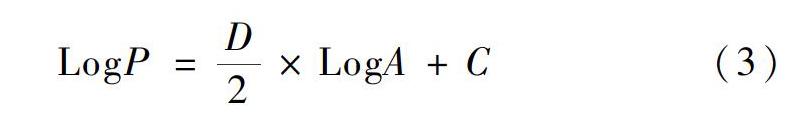
摘要：

实际生产过程中，超高性能混凝土（UHPC）的配制及性能往往受到原材料品质波动的制约。为此，基于最紧密堆积理论，采用改进Andreasen模型和最小二乘拟合算法，对现有UHPC基体中的粉料材料最緊密堆积配比进行了计算。随后参考计算结果设计了不同UHPC配比，用最大固相含量法测试了不同配比UHPC基体的堆积密度，根据相关标准测试了各个配比UHPC的力学性能、收缩性能，采用化学结合水法对胶凝材料水化程度进行了测试，采用SEM对基体3 d和28 d龄期的微观形貌进行了分析。结果表明：根据最紧密堆积理论进行配比设计，UHPC中的水泥用量大幅降低;优化后不同配比UHPC及其基体的力学性能与最大固相含量法测试的结果相吻合，得到的UHPC基体最大抗压强度为136.1MPa。总而言之，结合最紧密堆积理论和最大固相含量法进行UHPC配比设计，可以克服材料局限性，得到水泥用量较少并且性能更优的UHPC配比。

关 键 词：

超高性能混凝土; 配合比优化设计; 最紧密堆积理论; 最大固相含量法; 水化程度; 微观形貌

中图法分类号： TU528

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.07.033

0 引 言

超高性能混凝土（UHPC）是一种新型超高性能水泥基复合材料，它以水泥、超细粉体、细填料、细骨料、纤维、高性能减水剂为主要原材料，由于其配比中传统的粗骨料被细砂代替，因此其本质上是纤维增强的超塑化混凝土[1]。

UHPC的配制技术主要是基于最紧密堆积理论，根据不同原材料的细度分布，对原材料的颗粒堆积进行优化，即尽可能提高堆积密实度，这也是提高包括水泥在内的各种原材料的利用效率、UHPC性能和经济性的重要途径。目前，颗粒尺寸和堆积优化的方法有三大类[2]，其中使用最广泛的是优化曲线法中的改进Andreasen模型[3]。

由于这些方法都是建立在理论计算的基础上，实际应用中常常受到技术水平不够和原材料波动等的限制，因此如何采用快速有效的方法对不同配比混合料的堆积密度进行表征，得到最紧密堆积的配比是解决UHPC生产应用的一大难题。

本次研究的主要目的是通过最紧密堆积的配方设计方法对UHPC的配比进行设计，特别是根据有限的材料和理论计算实现最紧密堆积配方设计，并且采取相关方法对不同混合料的堆积密度进行表征，以指导实际UHPC配比调试。本文以石英粉、超细矿粉、微珠粉等取代水泥，主要采用改进Andreasen模型和最小二乘法对UHPC混合料的配比进行设计，并与最紧密堆积曲线进行拟合，同时采用最大固相含量法[4-5]对不同配比混合料的堆积密度进行了表征。此外，采用化学结合水法对不同配比、不同龄期UHPC基体的水化程度进行了对比[6-7]，采用扫描电镜（SEM）对不同配比UHPC在不同龄期的微观形貌进行了分析。

1 试验方案

1.1 原材料及配比设计

1.1.1 原材料

水泥（C）为华新水泥股份有限公司生产的P·O52.5水泥;水泥（C）、石英粉（Q）、微珠（MS）和超细矿粉（SG）化学组成如表1所列，表观密度及比表面积等参数如表2所列，粒径分布如图1所示;石英砂（S）粒径为0.212～0.840 mm;水采用自来水（W），满足JGJ 63-2006《混凝土用水标准》;减水剂（WR）为江苏兆佳建材科技有限公司生产的PC8010粉体聚羧酸减水剂，胶砂减水率为23%;消泡剂（D）为江苏兆佳建材科技有限公司生产的D130有机硅型粉末消泡剂;钢纤维（F）为直径0.16 mm、长12 mm的平直形钢纤维。

1.1.2 配比设计

本文采用优化曲线法中的改进Andreasen模型对UHPC的配比进行计算，公式如下[3]：

式中：P（D）为粒径为D的累计筛余体积百分比，%;D为颗粒粒径，μm;Dmin为体系中最小颗粒粒径，μm;Dmax为体系中最大颗粒粒径，μm;q为粒径分布模量，本文q取0.25。

根据图1中不同材料的粒径分布数据及改进Andreasen模型，采用Mathematics软件中的LeastSquares函数对粉料配比进行最小二乘法计算，计算结果如表3所列。可以看到该配比中水泥用量较低，而石英粉占60.8%，由此判断石英粉的掺量是影响粉料堆积密实度的关键。因此参照计算的结果固定水泥、超细矿粉、微珠三者的比例，测试了不同石英粉掺量条件下（0～60.0%）UHPC基体（指不掺钢纤维的UHPC，后文简称“基体”）的工作性能，发现在石英粉掺量大于粉料总量的50.0%后，基体工作性能受到极大影响。因此参考计算和试验结果以及基础基体配比S1，设计了不同石英粉掺量的基体配比，如表4所列（S2～S7）。配比中干混料（包括作为粉料的普通硅酸盐水泥、超细矿粉、微珠、石英粉以及骨料石英砂）的总量为100%，减水剂、消泡剂以及水等均以外掺干混料的质量分数表示，钢纤维掺量为基体的2.15%（体积分数），用水量为干混料质量的10.50%。利用各个配比全部粉料的粒度数据绘图，与目标曲线进行对比，结果如图2所示，可以发现随着石英粉掺量的提高，基体粒度分布曲线逐渐靠近目标曲线。

1.2 试验方法

1.2.1 堆积密度测试

UHPC堆积密度测试参照香港大学Kwan[4]和Wong[8]提出的湿堆积方法（也称最大固相含量法）来进行。

按照配比将全部粉料与砂预混好得到预混料，按照一定的水固比（体积比）将浆体搅拌均匀，然后将浆体倒入体积为V的容器中（本次研究中采用容积220 mL的圆柱形敞口玻璃容器），采用钢尺抹平浆体，测试其重量m。假如预混料是由不同的材料α、β、γ等组成的，那么以一定水固比搅拌得到的浆体的中固相的体积Vc可采用如下公式[4]进行计算：

式中：Vc为容器中固相的体积，mL;M为容器中浆体的质量，g;ρw为水的密度，g/cm3;uw为水固比;ρα、ρβ、ργ分别为材料α、β、γ的密度，g/cm3;Rα、Rβ、Rγ分别为预混料中α、β、γ的体积分数。

因此浆体的固相浓度可以采用式（3）[4]进行计算：

式中：Φ为该预混料在该水固比的固相浓度;Vc为容器中固相的体积，mL;V为容器的体积，220 mL。

1.2.2 水化程度测试

水化程度测试采用化学结合水法进行。硬化水泥浆体中的化学结合水以OH-形式存在，通过化学键或氢键与其他元素连接。在相同温度、湿度养护条件下，硬化水泥浆体中化学结合水量随着水化产物增多而增多，随水化程度提高而增大[9]。

而体系中化学结合水量Mcw可以通过式（4）[10]进行计算：

式中：Mcw为硬化浆体中化学结合水的重量，g;M105为硬化浆体在105 ℃下干燥至恒重后的质量，g;M1050为硬化浆体在1 050 ℃下灼烧2 h后的重量，g;LOI为粉料在1 050 ℃的烧失量。那么该硬化浆体的水化程度可以通过式（5）[10]进行计算：

式中：βt为养护龄期为t d时硬化浆体的水化程度;Mw为完全水化水泥浆体的化学结合水含量，g。

有研究对OPC（普通硅酸盐水泥）、GGBS（矿渣粉）、FA（粉煤灰）、SF（硅灰）等完全水化所需水量进行了测试，结果表明每克OPC完全水化结合水量为0.228 g，每克（75%OPC+25%FA）完全水化结合水量为0.217 g，每克（75%OPC+25%GGBS）完全水化结合水量为0.318 g，每克（90%OPC+10%SF）完全水化结合水量为0.256 g[11]。本次研究中S1～S7胶凝材料配比为普通硅酸盐水泥∶超细矿粉∶微珠=9∶2∶1，根据上述研究，粗略计算本体系中每克胶凝材料完全水化所需水量为0.284 g（此结果仅用于对不同配比中胶凝材料水化程度进行对比，不用于进行定量分析）。

1.2.3 其他测试方法

力学性能測试参照GB/T 17671-1999《水泥胶砂强度检验方法》，采用40 mm×40 mm×160 mm试件进行测试;

180 d收缩参照JC/T 453-2004《自应力水泥物理检验方法》进行测试，试件拆模测初长后置于干养（20 ℃，RH=65%）环境中，养护至规定龄期并测试其收缩率;

扫描电镜（SEM）采用日本Rigaku SU8020场发射扫描电子显微镜。

2 结果与讨论

2.1 堆积密度

分别测试了基体S1～S4及S7在不同水固比情况下的固相含量，结果表明：S1和S7的固相含量在水固比为0.230的时候最高，而S2、S3、S4的固相含量在水固比为0.225时最高。这可能是由于一定石英粉的加入能够改善基体的工作状态，提高基体的密实程度，填充颗粒堆积空隙所需水的比例减少，从而提供工作性能的水的比例提高，因而表现为浆体达到最大固相含量所需的用水量更少。当石英粉掺量达到30%后，虽然更接近最紧密堆积曲线，但是由于胶凝材料少，仅依靠水和少量的胶凝材料对骨料进行包裹，因此工作性能较差，表现为最大固相含量水固比与不掺石英粉的S1一样。由此可以判断，以这种湿堆积的方法测试粉料的堆积密度，测试结果同时受粉料的颗粒粒径分布和浆骨比影响;从另一个角度看，这种方法更能真实反映基体的堆积密实度、最小需水量以及工作性能等。

各组最大固相含量由大到小依次为S2、S3、S1、S4、S7，其中S1和S3的最大固相含量接近。

2.2 力学性能

分别测试了S1～S7不掺纤维及掺2.15%钢纤维在不同养护龄期的抗压强度，结果如图3所示。由图3（a）可知：在养护龄期为1 d和3 d时，基体抗压强度最高的为S1组，随着养护龄期延长到7 d和28 d，抗压强度最高的为S3组，其28 d抗压强度达到136.1 MPa。由图3（b）可知：掺钢纤维后，3 d强度最高的为S1组，而7 d和28 d抗压强度最高的为S2组，其28 d抗压强度达到171.1 MPa。由数据还可知，虽然S2和S3水胶比比S1大，并且水泥用量较少，但是其强度均高于S1（不论是UHPC还是基体），这与前文所提湿堆积法测试结果相吻合。

基体强度最高的为S3，而UHPC强度最高的为S2，这是因为S2中细颗粒较多，基体与钢纤维之间接触面积更大，因而结合更紧密，更能发挥钢纤维的作用效果[12]。因此要想得到高强度的UHPC，首先需要参照紧密堆积曲线和各个材料的粒径分布对材料配比进行优化，其次需要采用类似湿堆积的方法对基体在加水后的实际堆积密度进行测试，最后还需要测试基体与钢纤维的协同作用效果，得到最优的配比。本次研究中作为基体最优的为S2。

值得注意的是，掺石英粉最多的S6和S7，虽然水泥的用量仅占基体材料总量的25%左右，水胶比也很高，但是28 d基体抗压强度分别为110.5 MPa和98.9 MPa，掺钢纤维后强度分别为151.5 MPa和142.6 MPa。

2.3 水化程度及收缩

采用前文所述的方法对S1～S7各基体中胶凝材料的水化程度进行了测试，结果如图4所示。虽然无法准确定量评价各个配比中胶凝组分的水化程度，但是由于各组胶凝材料配比均一样，在假设骨料及石英粉不参与水化的条件下，仅对几组配比的水化程度进行对比。由图4可知，随着体系中石英粉掺量提高，水泥和矿粉、微珠粉等掺量降低，早期水化程度都逐渐提高，并且随着养护龄期的延长，各种胶凝材料水化更彻底，提高了资源和能源的利用效率，其中力学性能最优的S2中，胶凝材料28 d水化程度比不掺石英粉的S1提高了21.8%。

对不同配比UHPC在180 d之内的收缩率进行了测试，结果如图5所示。由图5可知，随着石英粉掺量的增加，胶凝材料用量的减少，S1～S7总体上收缩率逐渐增大。这是由于在固定水固比的情况下，胶凝材料用量越少，一方面会导致水胶比增大，胶凝材料水化反应迅速，导致化学减缩越显著，同时强度增长缓慢，对收缩变形的抑制能力越差[13];另一方面体系完全水化所需用水量减少，从而未参与水化的水越多，因此在早期会表现为干燥收缩增大。但是对比S1和S2可以发现：S2在14 d之后收缩均小于S1，这可能是由于在初期干燥收缩速率基本稳定后，基体颗粒形成的最紧密堆积体系导致体系空隙减少，即毛细孔细化或减少，此外由于S2水胶比更高，内部自干燥程度比S1略低，因而产生的自收缩减小[14]。

2.4 扫描电镜图像

对S1和S3基体进行扫描电镜分析，当龄期为3 d和28 d时，取扫描电镜分析样品并置于无水酒精中终止水化，进行真空干燥后进行扫描电镜测试，结果如图6所示。由图6（a）和图6（b）对比可以看到：在养护龄期较短时，S1基体呈松散颗粒堆积，颗粒之间空隙较大，而S3颗粒堆积更紧密。对图6（c）和图6（d）对比可以发现：随着养护龄期的延长，S1和S3由于水泥水化的发展，变得较密实，并且S3中可以看到大量棒状的钙矾石。

3 d强度S1大于S3，而28 d强度S3大于S1，由此推测：在养护龄期较短时，胶凝材料水化程度较低，堆积密实度对基体力学性能的影响较小，而在养护龄期较长时，随着胶凝材料水化程度的提高，颗粒间空隙被进一步填充，堆积密度更高的S3才表现出更优异的力学性能。

3 结 论

（1） 采用改进Andreasen模型和最小二乘拟合算法对粉料配比进行优化，得到了水泥用量较低、利用效率更高、工作性能更好和更优异的UHPC和基体，其28 d强度最高分别为171.1 MPa和136.1 MPa。

（2） 受原材料粒度分布的影响，完全符合最紧密堆积级配曲线的配比在实际应用中并非最佳配比，因此在采用改进Andreasen模型对颗粒级配进行优化后，应分别对配比优化后的湿堆积密度进行测试，通过测试可以筛选在加水搅拌的湿堆积体系中，用水量最少且能满足一定工作性能的基体配比。

（3） 从本次研究的试验数据来看，基体和钢纤维的协同作用效果也会影响基体的性能，因而导致UHPC和其对应基体的强度规律并非完全对应。因此在筛选出有限的配比之后需要对掺钢纤维后的基体进行评价，以确定性能最优的UHPC配比。

（4） 在早期胶凝材料水化程度较低时，颗粒堆积密实度对基体力学性能并没有决定性的影响，而随着养护龄期的延长，胶凝材料水化程度的提高会导致颗粒间空隙更进一步被填充，此时UHPC堆积密度的提高对其力学性能的提高起至关重要的作用。

参考文献：

[1] RICHARD P，CHEYREZY M.Composition of reactive powder concretes[J].Cement & Concretce Research，1995，25（7）：1501-1511.

[2] FENNIS S.Design of ecological concrete by particle packing optimization[D].Delft：Technische Universiteit Delft，2011.

[3] FUNK J E，DINGER D R.Predictive process control of crowded particulate suspensions[M].Berlin：Springer Berlin，1994.

[4] KWAN A K H，FUNG W W S.Packing density measurement and modelling of fine aggregate and mortar[J].Cement and Concrete Composites，2009，31（6）：349-357.

[5] WONG H H C，KWAN A K H.Packing density of cementitious materials：part 1—measurement using a wet packing method[J].Materials & Structures，2008，41（4）：689-701.

[6] ESCALANTE-GARCIA J I.Nonevaporable water from neat OPC and replacement materials in composite cements hydrated at different temperatures[J].Cement and Concrete Research，2003，33（11）：1883-1888.

[7] KJELLSEN K O，DETWILER R J，ODD E G.Backscattered electron imaging of cement pastes hydrated at different temperatures[J].Cement and Concrete Research，1990，20（2）：308-311.

[8] WONG H H C，KWAN A K H.Packing density of cementitious materials：measurement andmodeling[J].Magazine of Concrete Research，2008，60（3）：165-175.

[9] YU R，SPIESZ P，BROUWERS H J H.Mix design and properties assessment of ultra-high performance fibre reinforced concrete（UHPFRC）[J].Cement and Concrete Research，2014，56（2）：29-39.

[10] 王培銘，丰曙霞，刘贤萍.水泥水化程度研究方法及其进展[J].建筑材料学报，2005，8（6）：646-652.

[11] PANE I，HANSEN W.Investigation of blended cement hydration by isothermal calorimetry and thermal analysis[J].Cement and Concrete Research，2005，35（6）：1155-1164.

[12] 吳泽媚.超高性能混凝土中纤维与基体界面粘结性能多尺度研究[D].长沙：湖南大学，2017.

[13] 张君，陈浩宇，侯东伟.水泥净浆、砂浆及混凝土早期收缩与内部湿度发展分析[J].建筑材料学报，2011（3）：5-10.

[14] 安明喆，朱金铨，覃维祖.高性能混凝土的自收缩问题[J].建筑材料学报，2001（2）：61-68.

（编辑：胡旭东）

引用本文：

叶显，纪宪坤，吴文选，等.基于最紧密堆积理论的超高性能混凝土配比设计

[J].人民长江，2021，52（7）：198-203.

Mix proportion design of ultra-high performance concrete （UHPC） based

on closest packing theory

YE Xian1，JI Xiankun2，WU Wenxuan1，LI Lei1，ZOU Wei1

（1.Wuhan Ujoin Building Material Technology Co.，Ltd.，Wuhan 430083，China; 2.Wuhan Sanyuan Special Building Materials Co.，Ltd.，Wuhan 430083，China）

Abstract：

In the actual production process，the preparation and performance of ultra-high performance concrete （UHPC） are often restricted by the raw material quality.Therefore，based on the closest packing theory，the improved Andreasen model and the least square fitting algorithm were used to calculate the closest packing ratio of powder in the existing UHPC matrix.Then different UHPC mix proportions were designed according to the calculation results.The bulk density of UHPC matrix with different mix proportions was tested by maximum solid loading method.The mechanical properties and shrinkage properties of UHPC with different mix proportions were tested according to relevant standards.The hydration degree of cementing materials was tested by chemical combined water method，and the micro-morphology of the matrix at 3 d and 28 d was analyzed by scanning electron microscope.The results showed that the cement content in UHPC decreased significantly according to the proportion design based on the closest packing theory.The mechanical properties of UHPC and its matrix with different proportions after optimization were consistent with the test results of maximum solid loading method，and the maximum compressive strength of UHPC matrix was 136.1 MPa.In summary，UHPC proportion design based on the closest packing theory and the maximum solid loading method can overcome the limitations of materials and obtain UHPC proportion with less cement content and better performance.

Key words：

ultra-high performance concrete;optimization design of mix proportion;closest packing theory;maximum solid loading method;hydration degree;micro-morphology