万能式断路器温升试验与发热时间常数关系研究

张羽棠

（ 中国质量认证中心上海分中心，上海 201206 ）

关键字：低压电器；断路器；温升试验；计算模型；数据比对

0 引言

低压断路器作为保护电路安全的器件，应符合国家标准的相关要求。为测量万能式断路器在额定电流下运行时的具体温升值，需进行载流温升实验，以此防止其在正常运行时，部分零部件温度过高的情况发生。一般情况下，万能式断路器规定其接线端子最高工作温度不超过120℃，即温升值与环境温度的和不超过120℃，过高的工作温度致使断路器内部零件加速老化、损坏。万能式断路器的热量主要是由于其通入了正常的工作电流，以及母排和桥式触头上的电阻损耗，涡流损耗以及磁滞损耗，产生的热量一部分使得万能式断路器部件发热，一部分由外壳、母排散发到空气中。通过温升实验得出数据，经数学方法测出其发热时间常数，可快速估算稳定温升值，减少温升实验时间，有效缩减时间成本[1-3]。本文通过相关试验结果分析影响因素与万能式断路器温升之间的关系，推导部分影响因素与温升之间的关系式以及万能式断路器发热时间常数的计算模型。

1 温升

1.1 断路器安装

1）选取功能完备的断路器产品；

2）将所需测试的断路器依据相关要求配置在试验区域，同时确认连接正常、可靠，上电后设备正常稳定运行；

3）确保支架安置稳固，防止被试断路器在实验过程中跌落试验台。

1.2 试验环境

1.1.1 环境条件

试验过程中应避免阳光直射且没有其他可能影响环境的热源，防止结果受到额外冷暖气流影响，且在本次研究过程中的温升试验，试验场地中的风速不超过0.1m/s。

1.1.2 环境温度

试验周期的最后1/4时间周期内记录周围环境温度。测量时至少用2个温度检测器（温度计或热电偶），均匀分布在被试电器的周围，放置在被试电器高度的1/2处，离开被试电器的距离约为1m。

1.3 温升试验

1.3.1 热电偶准备

选用Agilent34970多用途测量仪、T型热电偶，接线端子温度采集工具如图1所示。

图1 接线端子温度采集工具

1.3.2 铜排选择

温升试验用导体参照表1进行选取。

表1 铜排选择对照表

1.3.3 被试品安装与接线

试验品按正常使用方式安装，并按标准规定的规格，长度连接试验导线（或铜排）。

端子如有多根电缆并联，应构成一束，并使每根电缆之间约有10mm 空气间隙，如端子上有多根铜排并联，则排与排之间应有铜排厚度的空气间隙。

对于试验电流小于400A且各极相同的产品，可采取各极串联，用单相电源试验。对于试验电流大于400A的产品应用三相电流进行试验，各相电流应平衡，每相电流在±5%的允差范围内，多相电流的平均值应不小于规定试验电流值。

对于接线端子拧紧存在力矩要求的产品应按规定力矩拧紧，对于其他接线端应拧紧至弹垫压平。对于由多个螺栓联结的接线端子，采用对角螺栓依次逐步拧紧；对于螺栓型接线端子，尽可能选用多股导线，均匀置于垫圈下，使压紧力达到平衡，安装前必须对联结导线端子及铜排端子进行必要清洁。铜排连接方式如图2所示。

图2 铜排连接方式

1.3.4 热电偶固定

固定热电偶测量端时，应选择合适的测量部位。尽量靠近测量端子连接处中点位置进行固定，同时尽可能不影响被测表面的散热性能，避免测量结果偏差。

本文中热电偶固定方式采用铝箔纸粘贴法，热电偶测量端置于被测部位，以铝箔纸完全覆盖热电偶焊头及热偶丝裸露部分，确保焊头与测量处始终保持良好接触，如图3所示。

图3 铝箔纸粘贴效果

1.3.5 温度采集与数据记录

通入额定工作电流，前后一小时内温度差距小于1K时，即可认为万能式断路器接线端子温度达稳定状态，可关闭电源，整理数据并记录。

2 发热时间常数

温升结果在1h内温度变化不超过1K时，即可认为此时万能式断路器温度达到稳定状态。该判定方法虽然可以较为准确得到温升值，但所需时间长、效率低，资源浪费大、不利于快速检测，而利用公式计算温升在工程测量中又较难测量接线端子的各项常数。因此，为快速推算万能式断路器的稳定温升，可测量发热时间常数，通过发热时间常数与温升曲线的关系式，推算万能式断路器稳定温升。

2.1 温升曲线模型

其中：J为电流密度，ρ为电阻率，Sc为有效接触面积。

极短时间内的发热功率为：

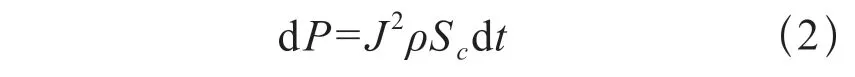
接线端子接触面微元接触电阻热功率为：

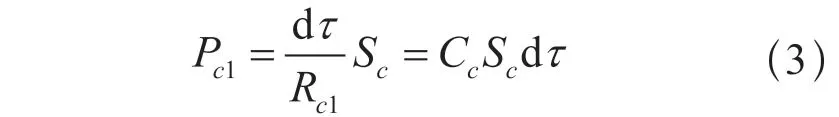
其中：Cc为接触面导热系数，dτ为接线端子与导体接触面温度差，Rc1为接触电阻。极短时间内的功率为：

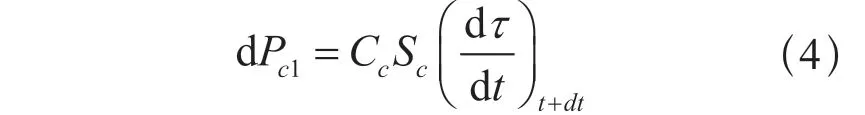
同样，产生在连接导线电阻上的热功率为：

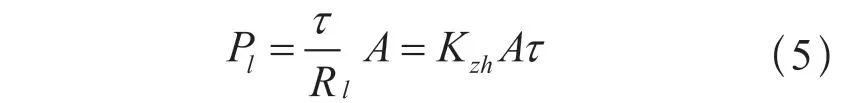
其中：A为到导线排侧表面散热面积，Kzh为导体散热系数。

加强交流合作，与中亚国家在农产品出口和消费市场培育等方面开展持续、便利、长效的贸易合作，形成规模有序的贸易环境。通过各类渠道，深入了解中亚各国的民俗风情、贸易政策、海关制度、动植物检疫制度、税收政策等，为全面开展贸易掌握情况。积极开拓中亚农产品市场，以品牌宣传为主线，以产品展示展览为载体，积极组织农产品企业在“一带一路”沿线国家和地区参加农产品博览会、交易会、洽谈会，把更多的出口企业、农产品推介到中亚市场。

极短时间内的功率为：

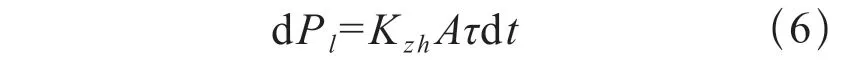
由热平衡原理可知：

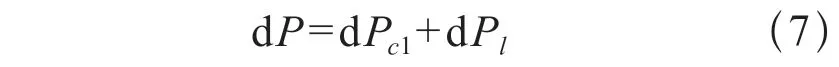
由前文整理可得：

解微分方程可得：

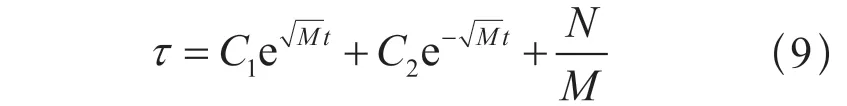
其中：M=KzhA/CcSc，N=J2ρ/Cc。

令：

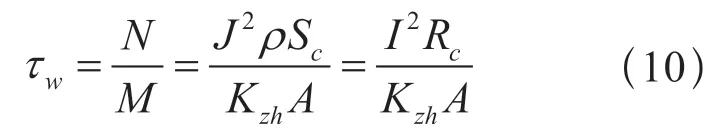
即为万能式断路器接线端子稳定温升，单位为K。

对于边界条件的定义：

将C1与C2带入式（9）可得万能式断路器温升曲线公式为：

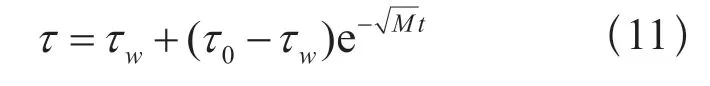
如设定起始温升为0℃，则式（10）可写为：

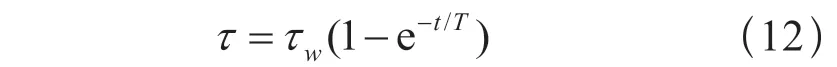
由式（12）可知，接线端子温升随时间增加呈指数上升规律。由于无法由公式准确得到在不同环境下接触面导热系数Cc，因此，需通过实验准确测得当前环境下的导热系数与发热时间常数T。

2.2 温升快速算法

运用最小二乘法拟合的曲线即为拟合曲线。最小二乘法拟合曲线即为拟合后曲线公式值与实验数据对应数据值的残差平方和最小曲线。由实验所得数据(xi,yi)，(i=1,2,3...N)，同时得出y关于x的函数关系y=F(x)。设实验数据xi存在残差δi=F(xi)－yi，(i=1,2,3...N)，要求所得曲线y=F(x)，使残差平方和最小，即：

最小二乘法即需要保证所得曲线的残差平方和最小。

合理选择拟合函数有助于减少残差平方和的大小。常用的回归方程有线性函数和非线性函数，如一元线性函数y=a+bx，多项式函数y=a0+a1x+a2x2+…+anxn，对数函数y=a+b1nx，指数函数y=aebx等。

通过上述公式推导，可知万能式断路器接线端子温升曲线符合指数函数曲线，因此选择式（11）作为拟合函数，将公式改写为：

两边同时取对数得到拟合方程线性型式：

则式（15）非线性问题可转化为一元线性问题。

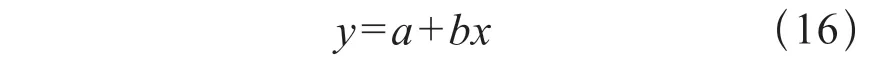
根据式（16）求解未知数b值，推测接线端子发热时间T常数值范围，从而根据式（14）推算接线端子的稳定温升。

运用函数polyfit，编写程序对接线端子温升数据进行曲线拟合。拟合曲线流程如图4所示：

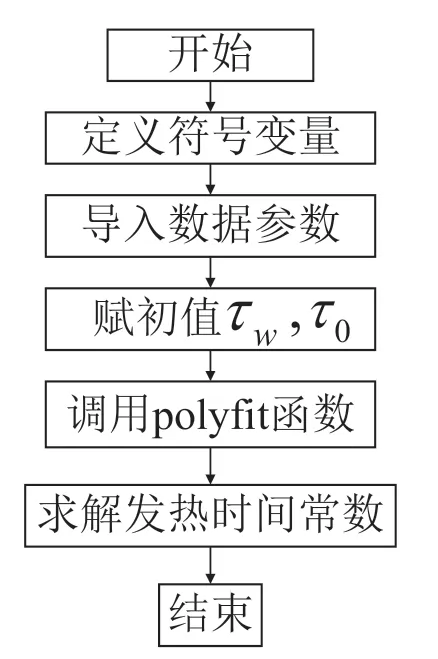
图4 拟合曲线流程示意图

由图4所示流程求解表2中万能式断路器温升实验数据的发热时间常数。

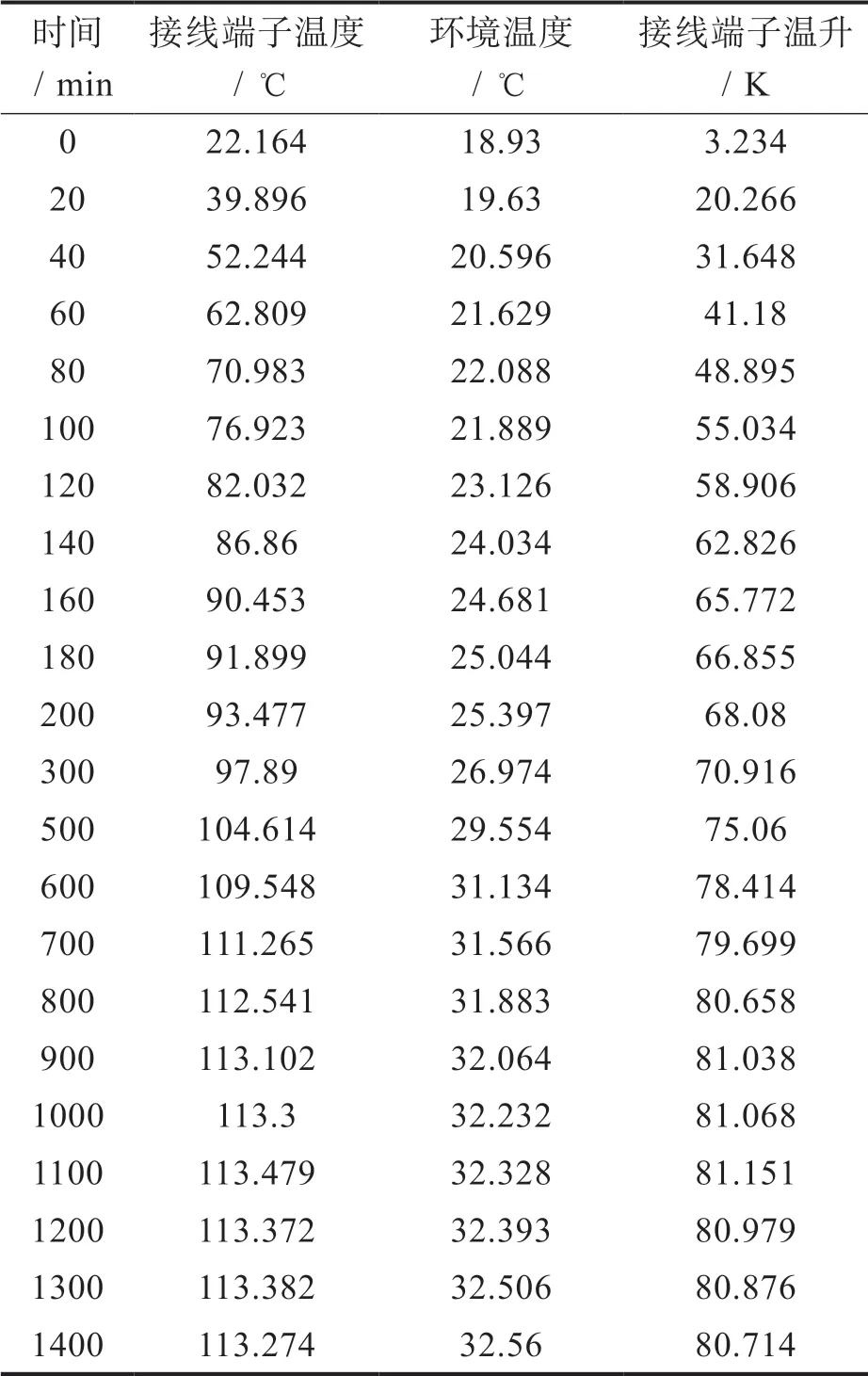
表2 万能式断路器接线端子温升数据

为了计算的有效性，定义初始温升τ0为3.234K，τw为81.152K。通过曲线拟合后可得：发热时间常数T为90。

在表2中找到时间为80min和100min数据，取这两组数据的中间值为51.9645，因此取时间T为90时，此时温升应为稳定温升τw的0.6321倍，采用中间值除以0.6321得出稳定温升τw为82.21K。可知万能式断路器的温升曲线公式为：

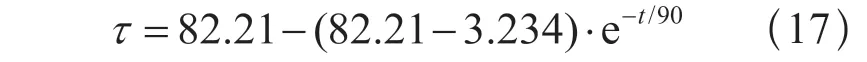
温升实验曲线与温升公式曲线如图5所示。

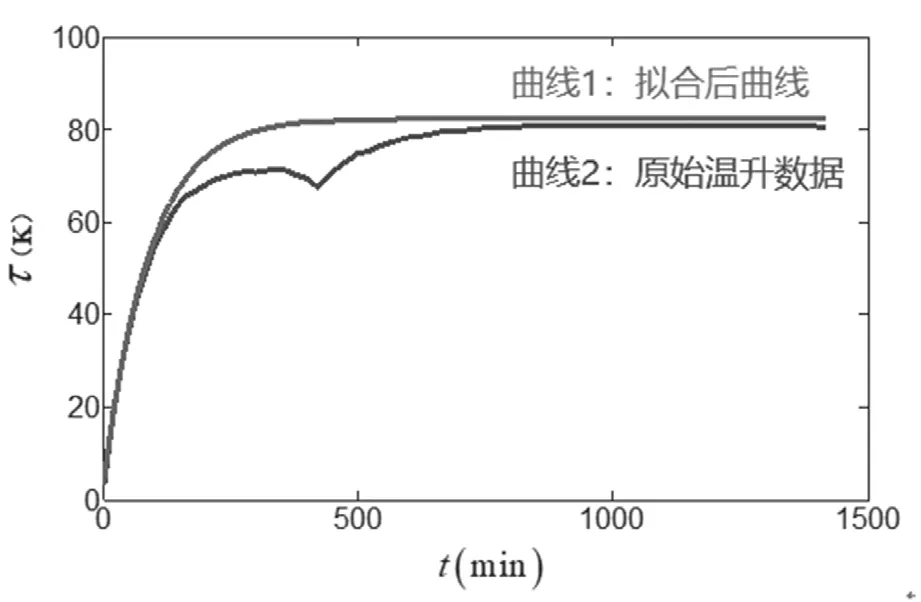
图5 温升实验曲线与温升公式曲线图

图5 中曲线1为拟合后的曲线，曲线2为原始数据曲线，横坐标为时间t，纵坐标为万能式断路器接线端子温升K。由图5可知通过最小二乘法函数polyfit拟合曲线与实际温升曲线重合度较高，基本可通过拟合后的曲线确定稳定温升值。表3为计算值与实际值对比。

表3 温升计算值与实际值对比

通过计算值与实际值的对比可知，计算值与实际值的差距较小，基本接近实际值，因此通过计算某一系列的万能式断路器发热时间常数，可快速估算接线端子温升，极大程度缩短实验周期，节省时间成本。

3 结语

低压断路器是电力系统内不可或缺的器件，其安全稳定运行关系人们的生命财产安全。作为低压断路器中最为复杂的万能式断路器，在高温高热环境下，将大幅降低其运行的稳定性。依据国家标准要求设计相关实验，通过实验结果分析影响因素与温升之间的数学关系式，推导万能式断路器发热时间常数计算模型，运用最小二乘法求得最佳计算值，通过软件将方法得以实现。经比对，计算数值与理论数值差异较小，证明设计的模型准确可靠。