基于层次分析法的加强层结构型式选定★
余隆丽 张晋芳 周郅炅 陈红豆 林 洁 张仁杰
(西华大学土木建筑与环境学院,四川 成都 610039)
1 概述
随着我国经济的快速发展,现代高层建筑正向着多功能、复杂构造及更美观发展,加之我国人均土地占有率不高,高层和超高层建筑已成为我国城市建筑的主要发展方向。随着结构高度的增加,水平荷载的影响程度随之加大,结构需要承受更大的侧向作用。当高层建筑的侧向刚度不能满足要求时,对于框架—核心筒结构、筒中筒结构等高层结构类型,一般利用建筑避难层、设备层空间,在框架与核心筒之间设置刚度较大的加强层,以此提高结构抗侧移的能力。选择一个合理的加强层方案十分重要。高层建筑是一项较大的工程,选择合理的加强层方案能最大程度的满足结构的安全性、经济性和实用性,减少高层建筑施工和运行过程中可能带来的损失。加强层方案的选择必须根据工程的总体刚度、施工、经济、空间以及用途等要求,综合考虑各方面的因素,选择加强层最为合适的部位、伸臂类型、框架梁柱的尺寸等。影响加强层方案的因素有很多,为了综合考虑到各个因素的影响程度,得出最优的加强层方案,本文运用层次分析法对各个因素影响程度进行量化,通过数值计算得出最佳方案,为实际工程加强层选择提供参考。
2 层次分析法在加强层结构选型中的应用
2.1 层次分析法基本原理[1]
层次分析法是T.L.Saaty教授于20世纪70年代中期确立的一种实用的多准则决策方法。它能够统一处理决策中的定性与定量因素,在一定程度上减少人的主观因素,使结果更趋于科学化,是一种实用、系统、简洁的方法。层次分析法的实际运用大概分为以下五步:
1)明确问题,建立问题的递阶层次结构。对影响结果的因素进行分类整理,根据不同层因素的重要性,以同一层次元素作为准则,其受上一层元素支配,并支配其下一层元素,构成层次之间的支配关系。
2)构造两两比较判断矩阵。根据插入折衷的提法对上下层之间元素的隶属关系进行分类。
3)由判断矩阵计算被比较元素的相对权重。通过计算进行一致性检验。
4)计算各层元素的组合权重。将第三步得到的计算结果进行适当组合,进行总的判断一致性检验。
5)分析数据,得出结论。层次分析法通过建立目标层、准则层、准则属性层和方案层的结构模型,影响因素两两比较判断得出最合适的结构型式。
2.2 建立层次结构模型
影响高层建筑加强层选型的因素有很多,实际工程中的选择偏经验,本文在理论分析和参考实际工程的基础上,综合考虑结构性能、建筑性能、经济性能和施工难度四个方面的因素[2-6]。
结构性能是指设置加强层对结构整体性能和局部性能的影响。高层建筑在其受侧向力较大的部位设置加强层,增加部分水平层的刚度,调节由风荷载引起的倾覆弯矩在核心筒和外框之间的分配比例,减小核心筒的倾覆弯矩,从而提高结构整体刚度,有效控制水平位移。但加强层刚度应当控制在一定范围内,结构层之间若产生过大的刚度突变,地震作用下的破坏和侧移容易集中在加强层附近形成软弱层,此时需要加强加强层及相邻层的竖向构件。加强层的设置同时会影响轴力在竖向构件之间的分配,进而影响结构整体和局部的竖向变形。
建筑性能主要考虑建筑物整体的美感和内部功能的实现。加强层一般设置在避难层,合理的结构形式,可使加强层作为高层建筑利用方式的分割层,使上下层的布置方式更加灵活,同时实现避难层或者设备层的功能。加强层大多位于高层建筑的中间层,不同形式的加强层也会改变建筑立面的样式和功能。
经济效应主要考虑修建过程中成本的投入和后期综合使用的经济效益。不同形式的加强层造价相差较大,建造过程中原材料的用量以及施工成本都要综合考虑。另外,加强层的合理设置可以有效改善结构的整体性能,从而使得剪力墙、筒体和柱等构件截面尺寸可以得到优化。利用建筑设备层和避难层的空间设置加强层,可较好地解决建筑底部或其他层的需要开高大空间的问题,从而满足建筑功能需求,间接提高经济效益。
施工难度对建筑物的造价和完成效率都会产生影响。加强层在施工组织时需要和整体结构施工相协调,所以不同形式的加强层对整个项目的施工组织影响较大。对于设计较为复杂的加强层,施工时有一些特殊的施工工艺,这部分也会提高整个施工难度。
按照层次分析法建立的模型如图1所示,其中A层为目标层,B层为准则层,C层为准则属性层,D层为方案层。

2.3 构造两两比较判断矩阵及一致性检验[1]
为了使各因素之间的重要程度对比,采用两两比较的方式得到量化的判断矩阵,引入1~9的比例标度,对于n个元素只需给出n(n-1)/2个判断数值,其余数值由1或者已给数值的倒数给出。两两比较的判断矩阵为:
A=(aij)n×n。
其中,元素aij表述对上一层元素而言,ai对aj的重要性指标。1~9标度含义如表1所示。

表1 标度的含义
通过判断矩阵计算其特征根λmax和特征向量ω。其中特征向量即本层次中各元素的重要性次序的权重。根据特征根λmax可计算出一致性指标:
(1)
将一致性指标C.I.与平均一致性指标R.I.进行比较,得一致性比例:
(2)
一致性指标R.I.的取值如表2所示。

表2 一致性指标R.I.的取值
当C.R.<0.1时,一般认为判断矩阵具有满意的一致性,且C.R.越小,结果越满意。
2.4 层次总排序
为了得到递阶层次结构中每一层次中所有元素相对总目标的相对权重,需要把前面得到的计算结果进行适当组合,即可计算得到本层次所有元素重要性的权数值,即层次总排序。例如在图1的最优加强层结构选型模型图中,先求出ωBA,再求出ωCB,由这两项可得出ωCA,通过计算得出ωDC后,结合ωCA可得出ωDA,即方案层对目标层的排序权值。
其中,ωij(i,j=A,B,C,D)表示的j层对第i层的排序权值,为一个向量。
3 工程实例
3.1 实例简介
以昆明科技金融中心加强层结构选型为例[7]。建筑外轮廓高度为204.2 m,结构高度为195.8 m。地上45层,1层~2层通高作为大堂,标准层层高4.2 m;地下3层,层高3.6 m。建筑形状为正方形切去一个倒L角,建筑核心筒采用非常规的L布置,且楼梯间位于塔楼外侧,建筑平面的不规则使得其受力较为复杂,结构扭转效应较为明显。设计采用钢支撑框架结构,采用H型钢梁作为楼面梁,电梯筒周边布置钢支撑,在设备层和避难层(10层,21层,32层)设置腰桁架,共设置三道水平加强层。
根据工程特点,初步设计以下五种加强层设计方案,并选择最佳设计方案:
方案一:于第21层,32层仅设置腰桁架;
方案二:于第10层,21层,32层仅设置腰桁架;
方案三:于第10层,21层,32层和屋顶避难层仅设置腰桁架;
方案四:于第10层,21层,32层设置腰桁架和伸臂桁架;
方案五:于第10层,21层,32层和屋顶避难层设置腰桁架和伸臂桁架。
3.2 实例计算
3.2.1 构造判断矩阵及其一致性检验C.R.
由全面分析得到的结构选型的影响因素,各个比较结果如表3~表16所示。

表5 C对B2的判断矩阵

表6 C对B3的判断矩阵

表7 C对B4的判断矩阵
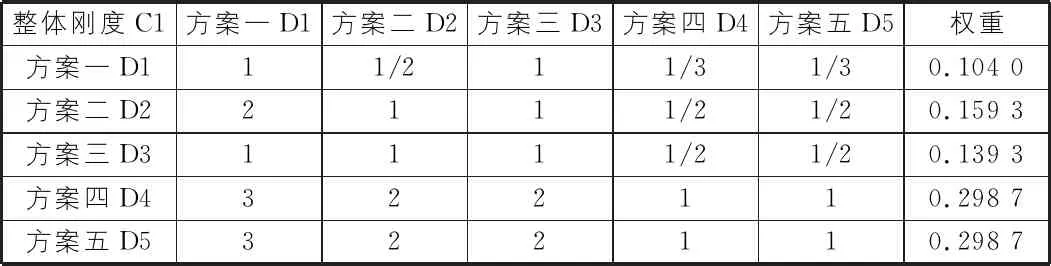
表8 D对C1的判断矩阵

表9 D对C2的判断矩阵
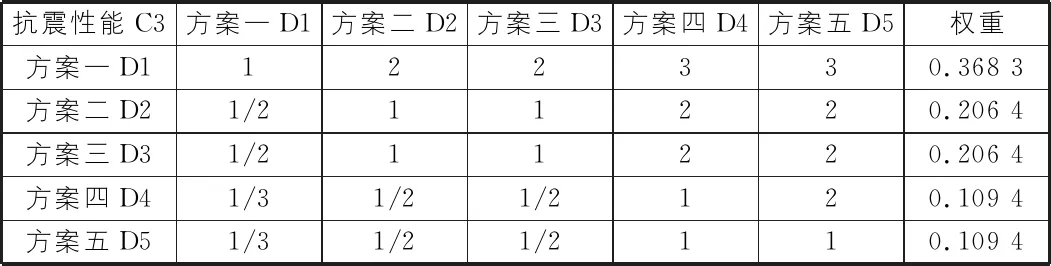
表10 D对C3的判断矩阵

表11 D对C4的判断矩阵

表12 D对C5的判断矩阵
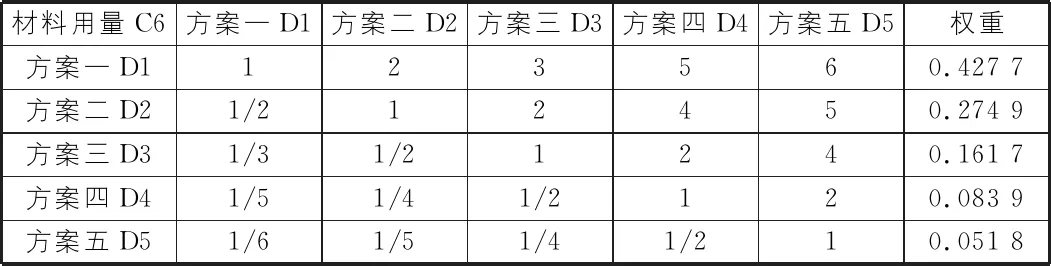
表13 D对C6的判断矩阵
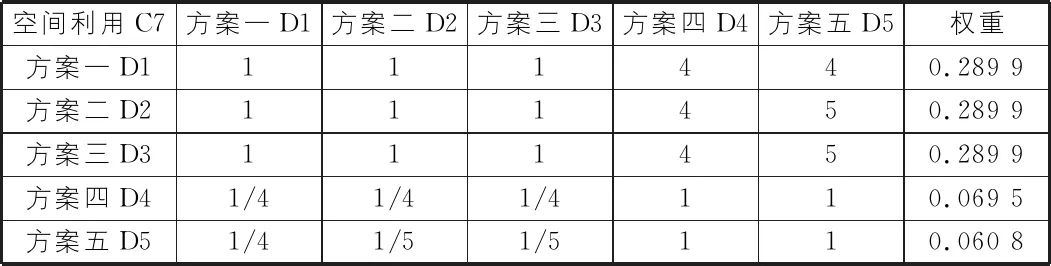
表14 D对C7的判断矩阵

表15 D对C8的判断矩阵

表16 D对C9的判断矩阵
一致性检验结果:λmax=4.010 7,C.I.=0.003 6,C.R.=0.004。
一致性检验结果:λmax=3.009 2,C.I.=0.005,C.R.=0.008 8。
一致性检验结果:λmax=2.000 0。
一致性检验结果:λmax=2.000 0。
一致性检验结果:λmax=2.000 0。
一致性检验结果:λmax=5.039 5,C.I.=0.009,C.R.=0.009。
一致性检验结果:λmax=5.078 4,C.I.=0.019 6,C.R.=0.017 5。
一致性检验结果:λmax=5.013 3,C.I.=0.003 3,C.R.=0.002 9。
一致性检验结果:λmax=5.064 7,C.I.=0.016 2,C.R.=0.014 4。
一致性检验结果:λmax=5.013 3,C.I.=0.003 3,
C.R.=0.002 9。
一致性检验结果:λmax=5.072 0,C.I.=0.018,C.R.=0.016 1。
一致性检验结果:λmax=5.006 0,C.I.=0.001 5,C.R.=0.001 3。
一致性检验结果:λmax=5.108 5,C.I.=0.027 1,C.R.=0.024 2。
一致性检验结果:λmax=5.026 9,C.I.=0.006 7,C.R.=0.006。
3.2.2 层次总排序
由上述结果整理为:
ωBA=[0.597 1,0.105 3,0.200 7,0.096 8]T;
ωCB1=[0.539 0,0.163 8,0.297 3]T;
ωCB2=[0.666 7,0.333 3]T;
ωCB3=[0.666 7,0.333 3]T;
ωCB4=[0.333 3,0.666 7]T。
根据ωBA和ωCB计算得到ωCA为:ωCA=[0.321 8,0.097 8,0.177 5,0.070 2,0.035 1,0.032 3,0.064 5]T。
由层次分析法得各方案按优排序如表17所示。

表17 方案排序
综上,根据层次分析排序结果选择方案一为最优方案,即于第21层,32层仅设置腰桁架。由层次分析法得出的结论与原文章选择方案有所出入,原文章选择方案二为最优方案,即于第10层,21层,32层仅设置腰桁架。原文章选择方案二的原因为:方案二对于结构X向层间位移角的富余更大,这一点只是考虑了结构刚度的影响,且从给出的X向层间位移角数据来看,方案二(1/317)并未比方案一(1/313)有太明显的优势。从原文现有给出的数据上来判断,方案一少设置一层加强层,综合考虑经济性等因素,应为最优方案。这一实例验证了多个条件影响下选择最优方案时采用层次分析法是可行的。
4 结语
加强层在高层建筑结构控制水平侧移方面具有很高的效率,但加强层的方案又很多,且形式选定普遍偏于经验性,不能完全综合考虑多方面因素。将层次分析法运用于最优的结构形式的选定,将定性的经验转化为定量的数学问题,可以综合考虑结构、建筑、经济、施工等多个方面的影响。本文所提出方法可以为实际工程加强层选型提供参考。

