有效把握点拨技巧 深化数学思考与理解

林玉芬

（福建省泉州市丰泽区第二中心小学）

《义务教育数学课程标准（2011年版）》指出：“课堂教学应激发学生的学习兴趣，调动学生的学习积极性，引发学生的数学思考，鼓励学生的创造性思维。”有效的点拨能激发学生的数学思考，深化对数学的理解。教学中，教师应以学生发展为本，掌握顺势、适时、深层和启发等点拨技巧，不断更新教育观念，大胆变革教学模式，提升数学课堂境界，进而提高教学效率。

一、顺势点拨，润物无声

顺势点拨是指教师根据学生的实际需要，顺应教学发展的要求，通过情境的提示，不漏痕迹地加以点拨，使学生在不知不觉中对问题的思考更加深入，理解更加到位。

如“淘气的校园”是北师版《义务教育教科书·数学》一年级上册“数学好玩”领域中“综合与实践”的起始课，共3 课时，本课是第一课时。教学参考书中推荐以小组合作的形式开展活动，让学生在活动中尝试搜集、记录数学信息，并根据发现的数学信息提出问题。一年级的学生虽然有数数的经验，也有一定的观察能力，但是，他们一般是看到什么就说什么，并不习惯按一定的顺序来观察，也少有分工与合作的经验。此外，根据年龄发育特点，他们的注意力不能太持久，观察、分析和表达能力也都有所欠缺。因此，就需要根据学生的特点组织教学，实施有效点拨，提高课堂效率。

考虑到一年级学生以直观思维为主的特点，我利用动画，以动态、直观的形式，创设“聪聪”和“跳跳”的卡通形象，“聪聪”寓意肯动脑筋，能想出好办法解决问题；“跳跳”寓意不动脑筋，解决问题不讲究方法。然后，我创设了跟着“聪聪”和“跳跳”一起参观淘气所在校园的情境，从中揭示活动任务：你能找到淘气所在校园里所隐藏的数学问题吗？要找到数学问题就得先找数学信息，我用课件逐一演示“跳跳”“聪聪”找数学信息的方法。

师：“跳跳”是怎么找的？“聪聪”呢？

生：“跳跳”是一会儿找这、一会儿找那跳来跳去地找；“聪聪”是慢慢地找。

师：“聪聪”是从哪里找到哪里？”

学生发现“聪聪”是从上到下按顺序地找，由此又想到除了按从上到下，还可以从左到右、由远及近或分成一类一类地找。学生对这两种收集数学信息方法还进行了讨论、对比，发现要像“聪聪”那样有序地找数学信息，这样才不会重复和遗漏。然后，我借助“‘跳跳’无序地找了很多数学信息，记不住，怎么办”引出了如何记录和如何合作记录，引导学生探究出一些常用的记录方法。

师：比如要记跳绳的人数，可以怎么记？

生：看谁跳得最多、标数字。

师：怎么表示跳绳？

生：画一个人在跳绳。

师：还可以只画什么？

生：只画一条绳子就可以。

在指导如何用简单的方法记录后，我让学生观看“聪聪”和“跳跳”分工合作的视频，接着同桌讨论如何合作收集记录信息的方法及注意事项，然后两人一组收集记录数学信息，最后展示、交流记录单。

小组展示记录单后，学生快速回答了“聪聪”和“跳跳”找到的数学问题，这时，我又引导他们根据记录单，提出数学问题。

生：跳绳有6人。

师：这是问题吗？（我的话音刚落，马上有学生反应到这是数学信息）

生：小树和跳绳的小朋友一共有几个？

这时，我让学生找出“小树以棵作单位，而小朋友以个作单位”，再让学生讨论：小树和人是同一类吗？当学生明白了这个问题后，就会找到“淘气的校园”中有关“加法和比多比少”的问题。学生在教室里找到了令我意想不到的数学问题，如“听课老师比学生多几人”“男生比女生多几人”“没戴眼镜的比戴眼镜的多几人”“一共几把椅子，几张桌子，几个窗户”等。

我通过顺势点拨，一方面激发了学生的学习热情；另一方面也唤醒了他们的学习和生活经验，让他们自然而然地意识到不能再像“跳跳”那样乱找信息，而要像“聪聪”那样按一定的顺序收集信息。学生能学以致用，利用记录的方法，以小组合作的形式进行实际操作，充分发挥了主体作用，获得了初步的数学活动经验，体验了数学学习的应用价值。这样，学生能更直观、更深入地感受到有序收集和记录数学信息的好处，进而能提高小组合作的实效，领悟到有序的数学思想方法。

二、适时点拨，精彩纷呈

苏联教育家巴班斯基指出：“教育与发展相统一和相互联系是教育过程的规律。”课堂应该成为培养、发展学生个性的土壤。我们需要创造一个开放、多元的环境，需要适时点拨，启迪学生的思维，让教育充满人文的色彩，让学生在自由的环境里充分发挥想象，释放活力，启迪思维。

如在教学北师版《义务教育教科书·数学》六年级下册“比例尺”一课时，我首先从生活入手进行点拔激趣：“老师暑假要去北京旅游，你能帮助我测算一下泉州到北京的路程吗？”学生兴趣盎然，各自在备好的“中国地图”上认真地测算。为测量两地的图上距离，有的学生用直线折测的方法沿公路线重叠或沿铁路线重叠，再将重叠过的线拉直，求出了图上距离；有的用直尺直接量两地的直线距离。我适时点拔：如何用图上距离求实际路程呢？他们边看图例，边讨论，边试做。有的用线段比例尺上每厘米代表的实际距离乘以图上距离，有的用图上距离乘以分数比例尺的分母，还有的用图上距离除以比例尺。讨论交流时，许多学生对直尺直接测量两地直线距离的方法提出疑问。最后，大家一致认为，确定旅游路线应该按图上两地铁路或公路的长度作为图上距离，然后求出两地的实际路程。用线段比例尺可以这样求：每厘米所表示的千米数×图上距离＝实际路程；用分数比例尺可以这样求：图上距离÷比例尺＝两地路程。有的学生用方程解，在设未知数时要点拔学生去思考：为什么要设成厘米为单位？为什么要注意化成更大一些的单位，如米、千米等？之后，我还让学生设计一种最佳的进京旅游方案。

在本节课中，学生体会到了用不同的思路来解决问题，那么，在出现线段比例尺的时候，他们就不会生搬硬套地用公式来解决了。这节课，学生兴趣浓厚，学得积极主动。反思整个教学过程，我认为，成功的关键就是把生活中的鲜活题材引入到了数学课堂上，给学生提供了一个展示激情、智慧与个性的大舞台，让他们在实践活动中获得了多方面的发展。

三、深层点拨，迎刃而解

深层点拨是指要在课堂上关注学生的“盲点”，拨疑为悟，引发学生深层次的思考。如有这样一道例题：小红前2 次测试的平均分是86 分，后3 次的平均分是91 分，她这5 次的平均分是多少分？一种解法是（86×2+91×3）÷5=89（分）；另一种解法是（91-86）×3÷5+86=89（分）。有的学生很难理解后一种解法，不知道为什么可以这么做。这时，就可以借助直观，数形结合，引导学生发现，每次的底数是86 分，多出来的部分可以平均分成5 份，再把这个平均数加上底数。在这个过程中，学生也更深刻地理解了算理。（如图1）

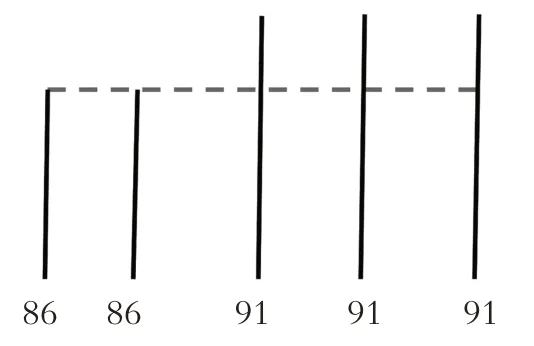
图1

四、启发点拨，水到渠成

叶澜教授说：“课堂应是向未知方向挺进的旅程，随时都有可能发现通道和美丽的风景，而不是一切都必须遵循固定的路线而没有激情的行程。”因此，教师要敏锐地捕捉学生认知和思维展开的最佳时机，适时加以点拨，高效推动教学进程。北师版《义务教育教科书·数学》四年级下册“三角形边的关系”一课中，有这样一个情境图：

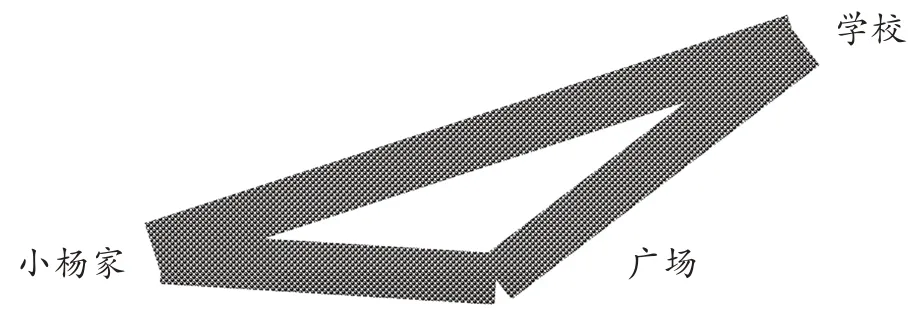
我先根据情境图提出问题：小杨从家到学校走哪条路更近？学生作出判断后，通过想象发现这两条路恰好围成一个三角形。我继续通过问题点拔学生引发猜想：“如果给你三根小棒当作三条线段，能否围成一个三角形呢？”接着，让学生动手操作，验证他们的猜想是否正确。在这个过程中，又会引发学生的思考：“围成”与“围不成”会与什么有关呢？从而揭题三角形边的关系；然后，让学生分小组讨论：如何研究比较三角形三边之间的关系？再全班交流，明确研究方向：每组都要任意两根小棒的长度之和与第三根小棒比较；学生进行小组活动，填写实验报告单，合作完各小组汇报自己的发现。我重点引导学生根据数据比较的结果理清“围成”与“围不成”的理由，从中总结出“三角形中任意两边之和大于第三边”。最后，提出质疑，验证规律：是不是所有的三角形任意两边之和都大于第三边呢？有什么办法证明呢？学生经过思考，在练习本上随意画三角形并通过量、算进行独立研究，并进行分类，借助不完全归纳法，推导出我们前面发现的结论具有普遍性，是正确的。在这些活动中，我为学生设置了有层次的问题，让他们进行充分的操作活动与思维活动，通过猜想、证实，深化的过程，更深入地理解了数学本质，发展了逻辑思维能力及推理能力，同时渗透了分类、比较与数形结合的思想，加强了探索精神的培养。

总之，点拨是一项重要的教学基本功。作为一线教师，应该努力使自己具备穿针引线、画龙点睛之功，用数学知识所蕴含的美好情愫，去点燃学生理想的火花，去陶冶学生的情操，使课堂教学真正达到一种宛若流水、水到渠成的境界。