不同人工神经网络在字母识别中的性能比较研究
李文正,崔皖新
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
0 引 言
人工神经网络是基于模仿大脑神经网络结构和功能而创建的信息处理系统,可以实现逼近、聚类和分类等诸多应用。目前已开发出多种类型的神经网络,这些网络可以根据复杂程度分为浅层神经网络和深层神经网络,并根据网络结构区分为前向神经网络和递归神经网络,具备不同的结构、激活函数和训练算法,面向不同的应用。在使用神经网络时,要结合网络的结构和原理了解网络的性能差异,才能在处理实际问题时更好地选用合适有效的网络[1]。
本文主要针对分类问题,选取感知器网络、BP网络和霍普菲尔德网络进行英文字母识别实验,并对这三种网络的表现进行对比研究。
1 创建网络
1.1 输入、输出矢量
创建网络前要先对字母进行数字化处理,从而获得网络的输入输出。
输入矢量根据26个字母确定。每个字母进行网格化处理后可以被表示为5×7的矩阵,进行简单变换即可生成一个行数为35的列向量,共有26个字母,因此输入矢量Pr×q是35×26的矩阵[2]。
每个输出包括25个0和1个1,其中1按照字母顺序(从A到Z的字母表顺序)从第1位移到第26位,因此输出矢量Ts×q可以被看作为26×26的单位阵。
字母A网格化处理如图1所示。
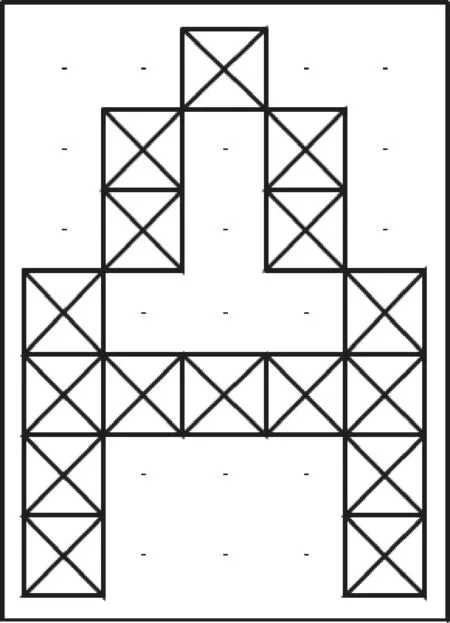
图1 字母A网格化处理
1.2 网络结构
感知器/BP网络:26个字母,每个字母35维0/1输入,故输入是35×26的矩阵,输出是维数为26的单位阵。感知器是单层网络,激活函数为二值函数;BP网络是双层网络,含有节点数为10的隐含层,隐含层和输出层的激活函数均采用S型激活函数[3]。
霍普菲尔德网络(离散):通过设置收敛域的方式进行字母识别,将每个待识别的字母作为35维特征空间内的一个稳定点(矢量的每一位均为±1),那么存在26个收敛域,待识别的字母会就近收敛到相近的收敛域完成归类识别。
2 三种网络的异同
这三种网络是均可执行分类操作的浅层神经网络[4]。结构方面,感知器网络和BP神经网络同属于前向神经网络,感知器网络为单层网络且激活函数为二值型函数,而BP神经网络具有一层隐含层,隐含层和输出层的激活函数均采用对数型激活函数(输出范围[0,1],易于收敛)。感知器网络和BP神经网络的基本训练算法均属于梯度下降法,基于网络输出和期望输出的偏差修正权值。2个网络的训练各自存在局限性:感知器网络计算简单但无法解决线性不可分的分类问题;BP神经网络虽然理论上进行充足的训练后可以带来更好的分类精度,但可能因训练时间较长,导致陷入激活函数饱和区或陷入局部极小值等。
霍普菲尔德[5]可根据26个字母的数字化结果在特征空间内设置平衡点和收敛域。同时霍普菲尔德网络属于全局递归的反馈神经网络,选用二值激活函数。
3 网络训练速度
感知器网络和BP神经网络均需进行带标签的监督式学习[6]。按照前文给定的输入、输出矢量训练,采取相同的误差平方和作为损失函数,以误差平方和达到10-4作为训练目标。
感知器网络训练结果如图2所示。

图2 感知器网络训练结果
感知器网络通过13次迭代完成训练。训练误差关于迭代次数的折线图如图3所示。
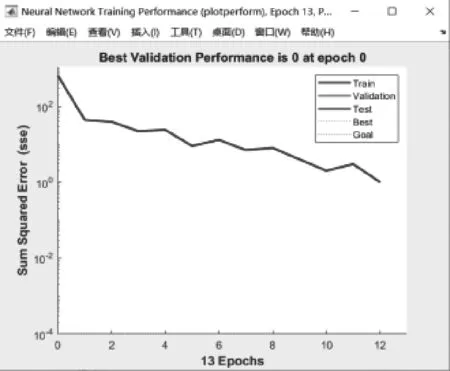
图3 感知器网络训练误差变化
对BP神经网络执行同样的训练。由于在原始BP算法基础上加入附加动量可以一定程度解决BP神经网络易陷入局部极小值的问题[7],因此在加入附加动量的基础上采用自适应学习速率(GDX)。
图4是经过多次调参后选取的比较理想的初始权值、初始学习速率和10个隐含层节点条件下BP神经网络训练误差关于迭代次数的曲线图。网络经过278次训练达到训练目标。

图4 附加动量自适应速率的误差变化
BP神经网络的训练算法对收敛速度的影响较大。替换训练算法为弹性梯度下降法(RP),采用trainrp指令进行训练,发现迭代次数大大减少。弹性梯度下降法训练误差变化如图5所示。
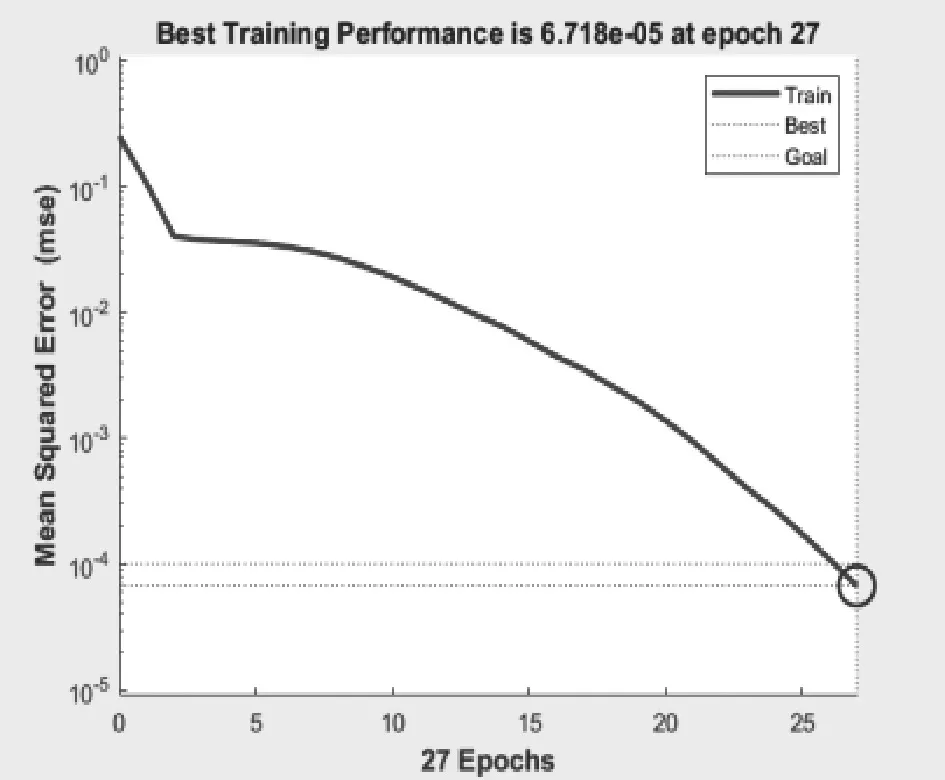
图5 弹性梯度下降法训练误差变化
当训练算法采用弹性BP算法后,会在计算时对符号的变化更加敏感,可更好地避免振荡问题。训练次数由278次减少到27次。
目前最高效的BP训练算法是LM算法,采用LM算法进行同样的训练只需六七次即可达到训练目标。LM算法训练误差变化如图6所示。
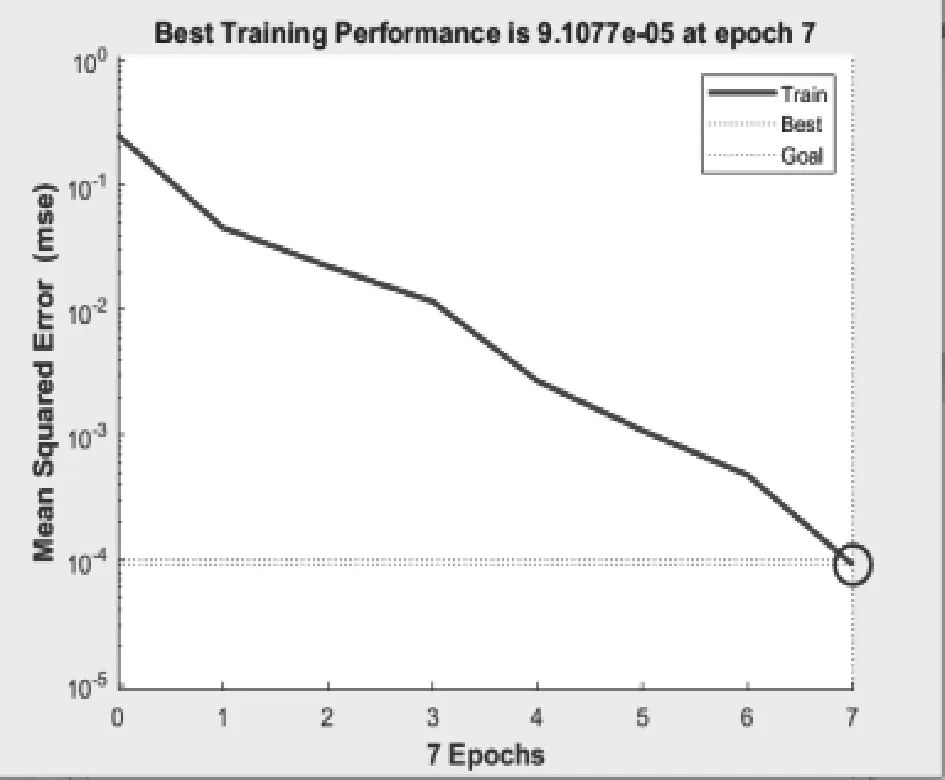
图6 LM算法训练误差变化
感知器网络和采用不同训练算法的BP神经网络的训练次数对比见表1所列。

表1 网络训练次数对比
可以看到,感知器网络训练算法简单,只需十余次训练即可达到目标,由于激活函数是二值型函数,因此可以很快地将训练误差训练至0。
BP网络的训练过程更加复杂,为达到较高精度,就需要更多的迭代次数。不同的BP训练算法对收敛次数的影响极大,虽然权值的初始化具有一定的随机性,但几种不同的训练算法对应的训练次数不在同一数量级。虽然改进的训练算法所需训练次数更少,但该训练算法每进行一次训练所涉及的计算会更加复杂(如LM法,结合牛顿法和梯度下降法,牵涉二次求偏导等复杂运算)。
4 网络的抗噪性能
抗噪性能指网络输出精度关于网络输入中添加噪声的灵敏度。在字母识别问题中,对网络输入添加噪声相当于影响字母的清晰程度。以字母A为例,对添加噪声前后的字母A做对比,如图7所示。

图7 无噪和有噪的字母A
噪声越大,字母越不清晰,越难以识别。检验网络抗噪性能的思路:在训练好的网络上使用不同噪声等级的输入进行仿真,计算仿真输出和实际期望输出间的偏差。噪声等级可以以0.02为间距步进,由低到高,绘出网络识别精度关于输入施加噪声的曲线。
在对网络训练时,也可加入噪声以求得抗噪性更优的网络。以感知器网络为例,采用无噪训练和0.4的噪声强度进行有噪训练,检验有/无噪网络的抗噪性。感知器网络的抗噪性能如图8所示。
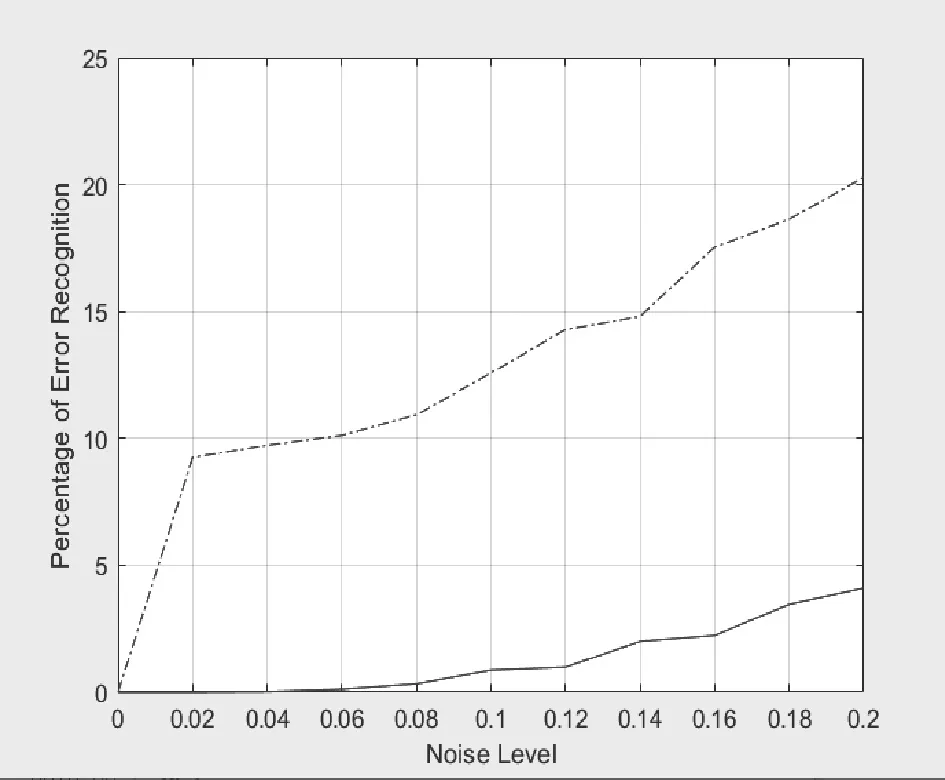
图8 感知器网络的抗噪性能
虚线代表无噪训练得到的网络,实线代表有噪训练得到的网络。选用的检验噪声等级从0步进至0.2,抗噪性能越好的网络曲线越低。显然,对于感知器网络而言,施加噪声进行训练的网络抗噪性能远强于无噪训练的网络抗噪性能。
通过对照选取性能表现良好的一组参数下的感知器网络和BP神经网络,与霍普菲尔德网络进行对比,将它们的误差-噪声曲线绘制在同一坐标系内,蓝色代表感知器网络,红色代表BP神经网络,绿色代表霍普菲尔德网络。对于感知器网络和BP神经网络而言,虚线代表无噪声条件下的训练,实线代表有噪声条件下的训练。测试噪声选取0∶0.02∶0.5。训练结果如图9所示。
从图9可以看出,感知器网络的抗噪性能最差,霍普菲尔德网络拥有最优的抗噪性能。同时,对于同一类网络而言,加噪训练的网络性能总是优于无噪训练的网络性能。

图9 抗噪性能对比(0∶0.02∶0.5)
加大测试噪声到0.8,结果如图10所示。

图10 加大测试噪声的抗噪 性能对比(0∶0.02∶0.8)
由图10可知,如果测试噪声进一步加大,BP神经网络的错误率上升趋势最稳健,即线性上升;感知器网络的错误率上升速率稍稍加快;霍普菲尔德网络在噪声进一步加大时,错误率基本呈指数级上升。测试噪声达到0.8时,BP神经网络表现最好,而霍普菲尔德网络表现最差。
感知器网络与BP神经网络的抗噪性能曲线上升趋势较相似,霍普菲尔德网络趋势陡峭,呈指数级上升。这归因于网络结构、原理和学习算法的差异[8]。网络抗噪性能对比见表2所列。
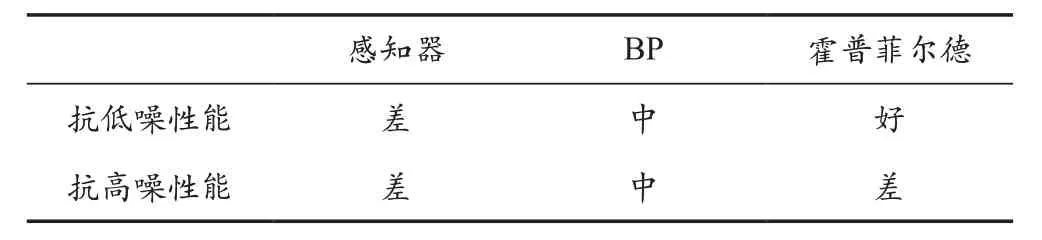
表2 网络抗噪性能对比
5 结 语
根据网络的训练和抗噪性能检验结果可以看出,三类网络在应用时处理同样的分类问题呈现出不同的特点。
感知器网络可以处理线性可分的分类问题,计算简单,训练时间短,迭代次数少。但训练的网络抗噪性能差,可考虑通过施加噪声进行更充分的训练来改善网络的抗噪性能。
BP神经网络需要更长的训练时间,使网络训练的更充分。可以采用改进的训练算法来缩短网络的训练时长。训练次数和采用的训练算法具有很大相关性,比较先进和高效的BP训练算法有牛顿法、共轭梯度法和LM法等(高效的改进训练算法牵涉更复杂的计算)。从网络性能上来说,BP神经网络无论是有噪训练还是无噪训练,相比感知器算法表现更加优异。BP神经网络同样可以通过进行更充分的有噪训练改善抗噪性能。
霍普菲尔德网络无需训练即可根据设定的平衡点直接生成[9]。可以看到,霍普菲尔德网络作为一种简单的递归网络,在可接受的噪声范围内进行字母识别优势明显。但霍普菲尔德网络在处理分类问题时存在自身缺陷:首先,待分类的输入矢量需控制好噪声强度范围,避免霍普菲尔德网络的错误识别率随输入噪声的增大而急剧升高;其次,霍普菲尔德网络可以处理的分类问题具有一定的局限性,因为其原理是设定平衡点和收敛域,不同于前向网络是建立黑箱系统调整权值,因此霍普菲尔德网络能处理的分类问题中,被分类的对象应当可以在特征空间内按照收敛域划分,无法建立输入到分类的映射关系[10];最后,霍普菲尔德网络可能会生成伪平衡点,进行错误的收敛,从而影响分类结果。

