砾石土粗粒含量对高土石坝蓄水期渗流的影响
常利营 叶发明 陈群

摘要:针对心墙砾石土可能出现粗粒含量不满足规范要求的问题,为了研究砾石土粗粒含量对坝体渗流安全的影响,以两河口心墙堆石坝为典型案例,建立坝体典型横剖面有限元模型。通过对心墙单元随机抽样并赋值较大渗透系数的方法模拟心墙内局部砾石土含量超标的情况,采用非饱和渗流理论对高土石坝蓄水期渗流进行数值模拟。结果表明:匀速蓄水工况下,无论砾石土粗粒含量是否超标,蓄水过程中心墙内最大渗透坡降都随蓄水速度的增加显著增大,对心墙渗透稳定不利;匀速蓄水过程中,砾石土粗粒含量超标时心墙内最大渗透坡降都比不超标时大,最大增幅约50%,但增大幅度与超标率和蓄水速度相关性不明显;采用合适的分期蓄水方案,即使心墙存在粗粒含量超标的情况,蓄水过程中心墙内坡降值都会明显降低,基本能够满足较短时间内完成水库蓄水并保证大坝渗流安全的工程需要,因此在实际工程设计中应合理设计蓄水方案。
关 键 词:
砾石土; 粗粒含量; 渗流安全; 蓄水速度; 分期蓄水
中图法分类号: TU641.1
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2021.06.024
1 研究背景
近年来,我国土石坝建设规模不断扩大,多座土石坝高度都在200 m以上,有的甚至超过300 m。这些高土石坝建设经验相对缺乏,超过现行规范的适用范围。初次蓄水对大坝安全至关重要,尤其是水库初次快速蓄水可能会造成一些安全事故[1],例如Teton宽心墙堆石坝溃决、Hyttejuvet窄心墙土石坝异常渗漏等。
针对高土石坝初次蓄水安全问题,一些学者进行了深入研究。王年香等[2]采用土工离心模型试验技术,对长河坝初次蓄水速率进行了研究。雷红军等[3]通过数值计算分析,研究了糯扎渡水电站水库初次蓄水时大坝的安全特性。林江等[4]对瀑布沟蓄水期的监测资料进行了分析,总结了蓄水期砾石土心墙渗压和土压力的变化规律。江沆[5]采用非稳定饱和-非饱和渗流理论,对双江口心墙堆石坝初次蓄水的非稳定渗流场进行了深入研究,提出了安全运行的建议。毕庆涛等[6]通过总应力法有限元计算,分析了不同蓄水方案对高土石坝应力变形的影响。王冕等[7]针对心墙砾石土填筑时粗细料分层情况开展了数值模拟研究,探讨了蓄水速度对心墙渗流场的影响。贺亚魏等[8]对某黏土心墙土石坝不同蓄水速度下的渗流场进行了数值试验,分析了不同工况上下游面坝坡的稳定性。黄华东等[9]研究了300 m级高土石坝蓄水期的应力变形性状,结果表明蓄水期心墙拱效应明显,易发生水力劈裂。
目前,高土石坝大都采用砾石土作为心墙防渗料。砾石土作为大坝的心墙防渗料有很大的优越性[10-11],如压缩性小、有利于避免水力劈裂裂缝、承载力高、便于机械施工等,但是由于地理、地质条件限制,很多地区的天然土料不能同时满足高坝防渗与强度性能要求。同时,由于料源的复杂性、开采的难度以及料源的储量受限等特殊情况[12]以及现场施工质量的差异,可能导致心墙出现局部砾石土粗粒含量(P5含量)超过50%,不满足DL/T 5395-2007《碾压式土石坝设计规范》要求。当P5含量超过50%时,其渗透系数会超过1×10-5 cm/s,可能会对土石坝初期蓄水安全产生不利影响,而目前在此方面的研究还很少。因此本文针对坝体心墙砾石土料存在局部粗粒含量超过50%的情况,采用ABAQUS有限元软件对坝体初次蓄水进行了数值模拟,分析了粗粒含量超标对坝体渗流场的影响,为高土石坝蓄水安全评价提供一定的参考依据。
2 计算原理及模型验证
2.1 计算原理[13-14]
ABAQUS软件采用位移有限元法,利用拉格朗日插值函数对虚功方程进行空间离散,得出计算域的有限元网格。计算域用有限元网格离散后,单元网格中流体的运动满足连续性方程,即Δt時间增量内流入的流体流量等于流体体积的增加速率。根据质量守恒原理,连续方程表示为
ddt(∫Vρwρow)=-∫SρwρowSrnnvwdS(1)
式中:n为渗流面S的法线方向;vw为渗流流速;ρow为流体参照密度,方程采用流体参照密度进行量纲一化。
渗流连续方程采用反向欧拉法近似积分,并将孔隙水压力视为变量进行有限元离散,孔隙流体的渗流行为采用Forchheimer定律,渗透系数表示式为
k=ks(1+βvwvw)k(2)
式中:k为饱和土的渗透系数;vw为渗流流速;β为反映流速对渗流系数影响的系数,当β=0时上述公式就简化为达西公式;ks为与饱和度Sr有关的系数,反映了非饱和土渗透系数与饱和土渗透系数的区别,ABAQUS中默认ks=Sr3,当饱和度为1.0时,ks=1.0。ABAQUS 同样是采用固定网格法求解非饱和渗流问题,基于非饱和土理论,将饱和与非饱和土放在同一分析域进行计算,孔压为零的位置即为渗流自由面。
2.2 模型验证
为了验证ABAQUS非饱和非稳定渗流计算程序的正确性,采用文献[15-16]中介绍的砂槽模型的试验资料。砂槽模型长315 cm,宽23 cm,高33 cm,模型材料为均匀砂,饱和渗透系数为0.33 cm/s,初始条件上下游水位均为10 cm,在时间0 s,上游水位骤升至30 cm,试验中蓄水后不同时刻砂槽模型中自由面的变化过程如图1中虚线所示。在ABAQUS中建立相应的数值模型,砂槽数值模型长315 cm,高30 cm,砂土材料特性与试验相同。数值模型采用四边形单元,共划分了448个节点、378个单元。图1给出了不同时刻试验模型和数值模型中自由面的位置变化,可以看出计算结果和试验结果比较接近,说明ABAQUS程序具有较好的可行性。图2给出了ABAQUS数值模型中不同时刻的孔压分布情况。
3 计算模型、方案和参数
3.1 计算模型
本文对两河口心墙堆石坝进行了简化,设计了如图3所示的计算模型:坝底高程为0.0 m,坝顶高程为295.0 m,坝顶宽16 m,顺河向坝底总长1 137 m。大坝心墙采用砾石土直立式心墙型式,心墙上、下游坡比均为1∶0.2,上游反滤层水平厚度为8 m,下游反滤层水平厚度为12 m,上、下游反滤层的坡比也都为1∶0.2,上、下游反滤层与堆石体间设置过渡层,上、下游过渡层的坡比均为1∶0.4,上游坝坡坡比为1∶2.0,下游坝坡坡比为1∶1.8。以坝体典型横剖面为基础建立了有限元模型,如图4所示。有限元单元分网基本尺寸为5 m,并对心墙进行了加密分网,计算模型共有单元35 664个,有限元计算中顺河流方向为X轴,坝轴线方向为Y轴,高程方向为Z轴,沿坝轴线方向取40 m。
3.2 计算方案
坝体初次蓄水工况下,上游初始水位为60 m,下游水位为30 m,上游水位从初始水位以不同速度上升至正常蓄水位(285 m),水位共上升225 m,下游水位保持不变。初始渗流场为上游初始水位对应下的孔隙水压力场,迎水面上游初始水位和正常蓄水位之间为变水头边界条件。结合工程实际,本文共选取了6种匀速蓄水速度来研究不同蓄水速度对坝体渗流的影响,蓄水速度分别为0.5,1.0,2.0,3.0,4.0,5.0 m/d。为了考虑分期蓄水的影响,参考已建土石坝蓄水情况,设计了如表1和图5中所示的6种分期蓄水方案。
根据该工程坝料的物理力学试验可知,当粗粒含量超标(即P5>50%)时,有部分试验土样渗透系数超过1×10-5 cm/s,因此为考虑最不利影响,粗粒含量未超标时心墙料渗透系数都取为1×10-5 cm/s,粗粒含量超标时渗透系数增大5倍。在实际工程中,心墙中存在粗粒含量超标(P5>50%)的区域一般是随机分布的,因此在进行有限元计算时对心墙所有单元按均匀分布进行随机抽样,并使抽得的单元体积占比(本文称为超标率)满足设定值。通过对超标单元和未超标单元赋予不同的渗透系数来考虑粗粒含量超标对坝体渗流的影响。本文共设计了4种超标率,如图6所示,方案C1~C4的超标率依次为2.5%,5.0%,7.5%,10.0%。从图6可以看出:粗粒含量超50%的单元在空间上都是均匀分布的,无局部集中情况出现。心墙粗粒含量全部满足规范要求时为基准方案。
3.3 计算参数
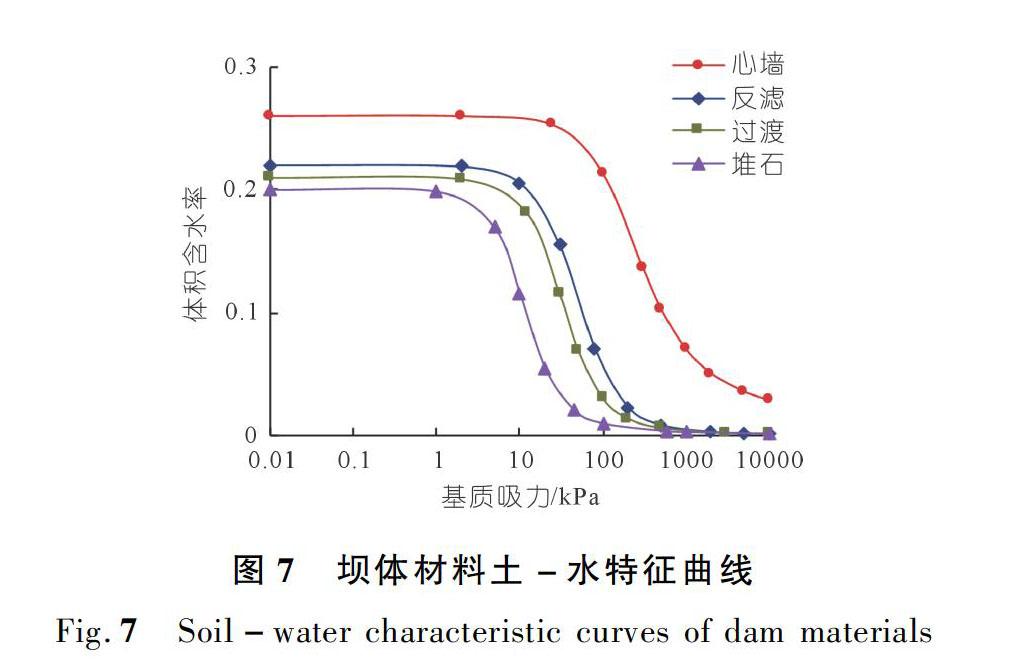
计算中坝体各材料的渗流特性计算参数如表2所列。坝体材料都为各向同性材料,其中心墙砾石土粗粒含量符合规范要求时(P5<50%),渗透系数采用1×10-5cm/s,粗粒含量超标时(P5>50%)渗透系数采用5×10-5cm/s。由于渗透系数相差小于一个数量级,且为了保证非稳定渗流计算较快收敛,因此两者采用相同的土-水特征曲线。结合工程经验,坝体材料的土-水特征曲线如图7所示,以描述土料的非饱和特性。
4 计算结果及分析
4.1 粗粒含量无超标
当心墙砾石土粗粒含量都满足规范要求时,大坝初次匀速蓄水工况下,随着蓄水高度的增加,上游堆石体内浸润面基本上和库水位同步上升,且基本和上游蓄水位齐平;下游堆石体内浸润面变化很小,且基本和下游水位齐平;心墙内浸润面比较靠近上游面,心墙下部(约1/4坝高以下部位)基本上处于饱和区,而中上部只有一小部分处于饱和区,心墙承担了大部分水头,心墙中孔压等值线分布比较光滑均匀。图8给出了不同蓄水速度下蓄水期末心墙内孔压等值线分布,从图中可以看出,随着蓄水速度的增大,心墙内的饱和区也明显减小,心墙中上部浸润面越来越陡。
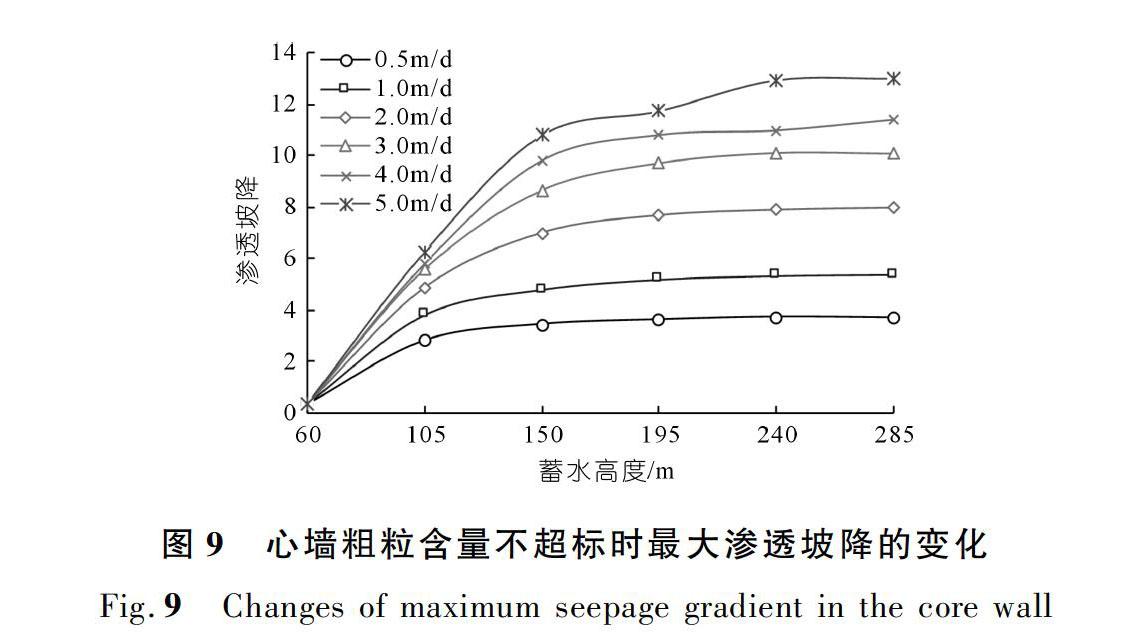
由于心墙土料渗透系数较小,其渗流基本满足达西定律,因此通过提取心墙单元渗透流速的计算值,根据达西定律即可求得各单元的渗透坡降。图9为不同蓄水速度下蓄水过程中心墙内最大渗透坡降的变化曲线。从图9可以看出:在某一蓄水速度下,随着蓄水高度的增加,心墙内最大渗透坡降在蓄水前期(蓄水高度150 m以下)增大較快,随后增幅变缓,蓄水期末心墙中的渗透坡降最大,且最大渗透坡降的位置都出现在心墙上游侧接近蓄水位高程附近,差别较小。随着蓄水速度的增大,蓄水过程中心墙内最大渗透坡降都会明显增大,当蓄水速度从0.5 m/d增加至5.0 m/d时,蓄水完成时心墙内坡降最大值从3.7增大至13.0,增幅超过200%,此时心墙上部砾石土料承受着很大的渗透力,对防止心墙发生水力劈裂不利。当蓄水速度过快时,在蓄水过程中心墙上部砾石土料的渗透坡降有可能超过其破坏坡降,容易发生渗透破坏,因此在实际工程中应对大坝蓄水速度进行一定的控制,以保证大坝的安全运行。
4.2 粗粒含量超标
图10给出了蓄水速度为0.5 m/d时蓄水期末C1~C4方案中心墙内孔压分布情况。当心墙中砾石土局部粗粒含量超过50%时,蓄水完成时心墙内孔压等值线的分布规律与基准方案时比较一致,但是等值线都不再光滑平顺,且随着超标率的增大,等值线弯曲程度也更加明显。蓄水过程中,心墙内饱和区的分布范围也基本相同。
当心墙局部粗粒含量超过50%时,蓄水过程中心墙内最大渗透坡降的变化曲线如图11所示。从图11可以看出:蓄水速度一定时,在蓄水过程中心墙内的最大渗透坡降都比基准方案(不超标)时大,且增大的幅度与超标率和蓄水速度的关系都不明显,当粗粒含量超标率在10.0%以内时,相比于不超标情况,最大渗透坡降增幅都在50%以内;随着蓄水速度的增加,蓄水过程中心墙内最大渗透坡降也明显增大。因此在心墙存在粗粒含量超标时,对坝体的蓄水速度更应该进行一定的控制,以避免心墙内砾石土产生过大的渗透力,影响坝体渗流安全。
从图11可看出:在蓄水中后期(蓄水高度150 m以上),心墙内最大渗透坡降波动增大,这是因为超标单元的存在会使心墙内无超标单元中的渗透坡降发生改变,因此受超标单元的影响,心墙内的最大渗透坡降值会有一定的波动。从计算结果看,最大坡降的位置都位于心墙上游侧接近蓄水高度附近的无超标单元处,差别较小。
4.3 分期蓄水的影响
当心墙粗粒含量无超标时,不同分期蓄水方案下心墙内最大滲透坡降的变化曲线如图12所示。从图12可以看出:相比匀速蓄水工况,本文设计的6种分期蓄水方案最大坡降所在位置与匀速蓄水时基本相同,但分期蓄水过程中心墙的最大渗透坡降明显降低,因此能更有效地保证大坝在蓄水期的渗透稳定安全。
在方案1下,前期快速蓄水到105m时心墙内的坡降达到最大值5.6,之后缓慢升高水位,心墙内的渗透坡降明显降低,并在之后的蓄水过程中基本保持不变(约3.7)。
对于方案2~4,在蓄水前期(蓄水高度105 m之前)心墙内最大渗透坡降都迅速增大,之后增速变缓,心墙内的渗透坡降都在蓄水完成时达到最大值,分别为9.1,8.3,7.0;蓄水过程中方案2和方案3心墙内的坡降值相差也较小,说明蓄水时间稳定为30 d能明显降低心墙内的坡降,继续增大稳定期的时长对坡降的改善不明显;相比方案2,采用方案4后蓄水过程中心墙内的坡降值有较明显的降低,说明缩短稳定期间隔有利于降低蓄水过程的坡降值。
对于方案5,在快速蓄水时,心墙内渗透坡降上升,在缓慢蓄水时,心墙内渗透降低,在每一次快速蓄水结束时,心墙内的最大渗透坡降都要高于其他5种分期蓄水方案。
对于方案6,与方案5一样采用交替蓄水速度进行蓄水,但交替蓄水间隔变短。由图12可以看出:蓄水过程中心墙内的最大渗透坡降变化规律与方案5明显不同,随着蓄水高度的增大坡降值先逐渐增大,在蓄水高度195 m时达到最大值7.4,之后又有所降低。
方案6的总蓄水时间比方案5短,方案4的总蓄水时间也比方案3短,但蓄水过程中心墙内坡降值都更低,说明采用合适的分期蓄水方案,也可以在较短的时间内完成水库蓄水并保证大坝的渗透稳定。在实际工程中,可以根据需要,结合本文计算所得的一些规律,对大坝实际蓄水过程进行优化设计,以提出更合理的蓄水方案,保证蓄水过程中大坝的安全运行。
针对心墙砾石土粗粒含量超标10.0%(C4)的情况,采用分期蓄水方案4进行了渗流计算,以研究粗粒含量超标时,分期蓄水方案对心墙内渗透坡降的影响。图13给出了分期蓄水工况下C4中心墙内最大渗透坡降的变化曲线。从图13可以看出,采用分期蓄水方案4后,相比于5.0m/d匀速蓄水,心墙内的渗透坡降也明显降低,且相比于无超标的情况,渗透坡降最大值也只增加了约为20%,由此说明,采用分期蓄水方案4,即使心墙存在粗粒含量超标的情况,在蓄水过程中心墙内的渗透坡降出现超过允许坡降的可能性仍然较低,大坝渗透稳定基本可以得到保证。
5 结 论
本文针对心墙砾石土料可能存在局部粗粒含量超过50%的情况,对高土石坝初次蓄水进行了数值模拟,探讨了粗粒含量超标以及分期蓄水对坝体渗透安全的影响,得出以下结论。
(1) 匀速蓄水工况下,随着蓄水速度的增加,对于粗粒含量无超标和有超标的情况,蓄水过程中心墙内最大渗透坡降都有显著增加,最大增幅超过200%,对防止心墙发生水力劈裂不利。
(2) 匀速蓄水工况下,心墙粗粒含量超标时,蓄水过程中心墙内的最大渗透坡降都比无超标时大,且增大的幅度与超标率和蓄水速度的关系都不明显,超标率在10.0%以内时,最大渗透坡降增幅都在50%以内。
(3) 采用合适的分期蓄水方案,即使心墙存在粗粒含量超标的情况,蓄水过程中心墙内坡降值都明显降低,能够满足较短时间内完成水库蓄水并保证大坝渗透稳定的工程需要。
实际工程中,蓄水情况更加复杂,一般蓄水和填筑同时进行,因此有必要结合实际蓄水工况进行更加全面的研究,并结合监测成果进行对比分析。
参考文献:
[1] 汝乃华,牛运光.大坝事故与安全[M].北京:中国水利水电出版社,2001.
[2] 王年香,章为民,张丹,等.高心墙堆石坝初次蓄水速率影响研究[J].郑州大学学报(工学版),2012,33(5):72-76.
[3] 雷红军,冯业林,刘兴宁.糯扎渡水电站蓄水速度对心墙堆石坝安全的影响研究[J].大坝与安全,2012 (5):1-5.
[4] 林江,陈佳伟,周志辉.瀑布沟大坝蓄水期心墙应力分析[J].长江科学院院报,2013,30(5):42-46.
[5] 江沆.双江口心墙堆石坝初次蓄水及库水位骤降非稳定渗流分析研究[D].南京:河海大学,2008.
[6] 毕庆涛,王平易.不同蓄水方案对高土石坝应力变形的影响[J].人民黄河,2009,31(7):87-91.
[7] 王冕,陈群.库区蓄水速度对不均匀心墙渗流场的影响[J].地下空间与工程学报,2014,10(增2):1794-1799.
[8] 贺亚魏,孟军省,刘雪梅.水位升降对粘土心墙土石坝渗流稳定性分析[J].武汉大学学报(工学版),2008,41(5):92-96.
[9] 黄华东,郭张军,韩耀铭,等.300m级超高斜心墙和直心墙堆石坝应力变形分析[J].水利水电技术,2017,48(2):37-44.
[10] 朱建华,游凡,杨凯虹.宽级配砾石土的防渗性及反滤[J].岩土工程学报,1993,15(6):18-27.
[11] 张丙印,袁会娜,孙逊.糯扎渡高心墙堆石坝心墙砾石土料变形参数反演分析[J].水力发电学报,2005,24(3):18-23.
[12] 保华富,谢正明,庞桂,等.长河坝水电站大坝砾石土心墙填筑质量控制[J].云南水力发电,2015,31(5):20-25.
[13] 张晓咏,戴自航.应用ABAQUS程序进行渗流作用下边坡稳定分析[J].岩石力学与工程学报,2010,29(增1):2927-2934.
[14] 費康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010.
[15] 吴梦喜,高莲士.饱和-非饱和土体非稳定渗流数值分析[J].水利学报,1999(12):38-42.
[16] 张培文,刘德富,黄达海,等.饱和-非饱和非稳定渗流的数值模拟[J].岩土力学,2003,24(6):927-930.
(编辑:郑 毅)
Influence of coarse-grained content in gravelly soil on seepage of high
earth-rock dam during impoundment
CHANG Liying1,YE Faming2,CHEN Qun3
(1.College of Safety Engineering,Henan University of Engineering,Zhengzhou451191,China; 2.Power China Chengdu Engineering Corporation Limited,Chengdu 610072,China; 3.State Key Laboratory of Hydraulics and Mountain River Engineering,Sichuan University,Chengdu610065,China)
Abstract:
The coarse-grained content in core wall gravelly soil may be larger than 50%and this does not meet the standard requirement,which may have a great influence on seepage safety of high earth-rock dam.A finite element model was established based on the typical dam section of the Lianghekou core wall rockfill dam.Through random sampling,the elements in the corewallwere assigned with high permeability coefficient to simulate the case of local coarse-grained content exceeding 50%.The influence of coarse-grained content in the gravelly soil was studied according to the unsaturated seepage theory.The results show that the maximum seepage gradient in the corewall increases greatly with the impounding speed under even impounding,no matter the coarse-grained content exceeds 50% or not,which is adverse for seepage stability of core wall.For the case that the coarse-grained content is larger than 50%,the maximum seepage gradient during impoundment is greater than that of case that the coarse-grained content is not larger than 50%,and the growth rate is up to 50%,however the growth of maximum seepage gradient has a weak relationship with the un-attainment rate and the impoundment speed.By adopting a suitable staging impoundment scheme,the maximum seepage gradient has an obvious decrease even if the coarse-grained content is larger than 50%,which can meet the demand of safe impoundment within a short time,so the impoundment scheme should be designed appropriately in engineering practice.
Key words:
gravelly soil;coarse-grained content;seepage safety;impounding speed;staging impoundment

