王甫洲水利枢纽泄水闸闸墩安全监控指标拟定

殷晓慧 费大伟 黄耀英 丁胜勇 任明喜

摘要：大坝安全监控指标的拟定可以有效监控水库大坝的长期运维情况，目前关于最大熵法与传统经典概率密度函数法拟定监控指标之间的对比研究成果不多。以王甫洲水利枢杻泄水闸闸墩位移监控为例，选取不利荷载工况下的监测资料系列组成小子样，分别采用K-S检验法和最大熵法确定极值概率密度函数，进而采用小概率事件法拟定监控指标。研究结果表明：由K-S检验法确定的泄水闸典型闸墩水平位移极值概率密度函数基本满足正态分布，且与最大熵法确定的概率密度函数曲线接近，对于两种概率密度函数利用小概率事件法拟定的位移监控指标也较为接近。

关 键 词：

监控指标; 闸墩位移; 最大熵法; K-S检验法; 王甫洲水利枢杻

中图法分类号： TV698.1

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.06.030

大坝安全监控指标是对已建大坝的荷载或效应量所规定的安全界限值[1]。拟定大坝安全监控指标，对识别险情、保障大坝安全具有重大意义，是实现大坝安全运行的关键[2]。因计算方便，实际工程多采用数理统计法拟定大坝安全监控指标，其中经典概率密度函数与典型监控效应量的小概率法[3-4]相结合应用得最为广泛，即通过分布检验确定出样本的概率密度函数，再由小概率法拟定监控指标。然而，由于实际监测效应量的小子样分布类型可能并不完全符合典型的分布函数（如正态分布、对数正态分布和极值I型分布等），这导致基于经典概率密度函数来估计大坝安全监控指标可能存在一定的误差。最大熵法的出现为拟定大坝安全监控指标提供了一种新的方法，最大熵法不需要事先假设分布类型，直接根据各基本随机变量的数字特征值进行计算，这样就可以得到精度较高的概率密度函数。

近年来，最大熵理论在社交网络用户关系分析模型[5]、电网故障诊断[6]、土壤重金属含量空间预测[7]等方面取得了较好的应用效果。有学者对其在大坝安全监控指标方面进行了探索，丛培江等[8]运用最大熵原理从理论上推导了大坝监测数据的熵概率密度函数模型，并给出了大坝安全监控指标的计算方法;马文丽等[9]基于最大熵理论拟定了陈村水库坝顶水平位移监控指标;殷详详等[10]基于熵理论对锦屏一级拱坝拟定了空间变形预警指标;李翔宇等[11]利用最大熵理论拟定了锦屏一级高拱坝施工期及蓄水期的弦长监控指标。上述研究多数仅利用最大熵法这一种方法来拟定监控指标，但目前关于最大熵方法拟定的变形监控指标与传统确定概率密度函数方法拟定监控指标之间的对比较少。因此本文利用王甫洲大坝较长时间序列的监测值，以王甫洲大坝泄水闸典型闸墩为例，采用K-S检验法和最大熵法分别确定概率密度函数，进而采用小概率事件法拟定监控指标，进行两种方法的对比分析。

1 基本原理

根据工程实测资料，首先选取不利荷载工况下的监测效应量组成一个子样本空间X={xm1，xm2，xm3，…，xmn}，并估计其统计特征值：

x=1nni=1xmi（1）

σx=1n-1ni=1x2mi-nx2（2）

然后应用统计检验法（如A-D法、K-S法）对该子样本空间进行分布检验，确定概率密度函数f（x）的分布函数F（x）（如正态分布、对数正态分布和极值Ⅰ型分布等）。

由于最大熵法不需要事先假设分布类型，直接根据各基本随机变量的数字特征值进行计算，这样就可以得到精度较高的概率密度函数，为此，采用最大熵法来代替统计检验法。基于最大熵法拟定泄水闸变形监控指标的步骤如下：

（1） 首先基于实测极值样本X={xm1，xm2，xm3，…，xmn}计算极值样本的各阶原点矩，采用拉格朗日乘子法调整概率密度函数f（x），使熵H（x）达到最大值，求解出拉格朗日乘子系数λ0和λi（i=1，2，…，n）。得到最大熵概率密度函数的解析形式如下：

f（x）=exp（λ0+Ni=1λixi）（3）

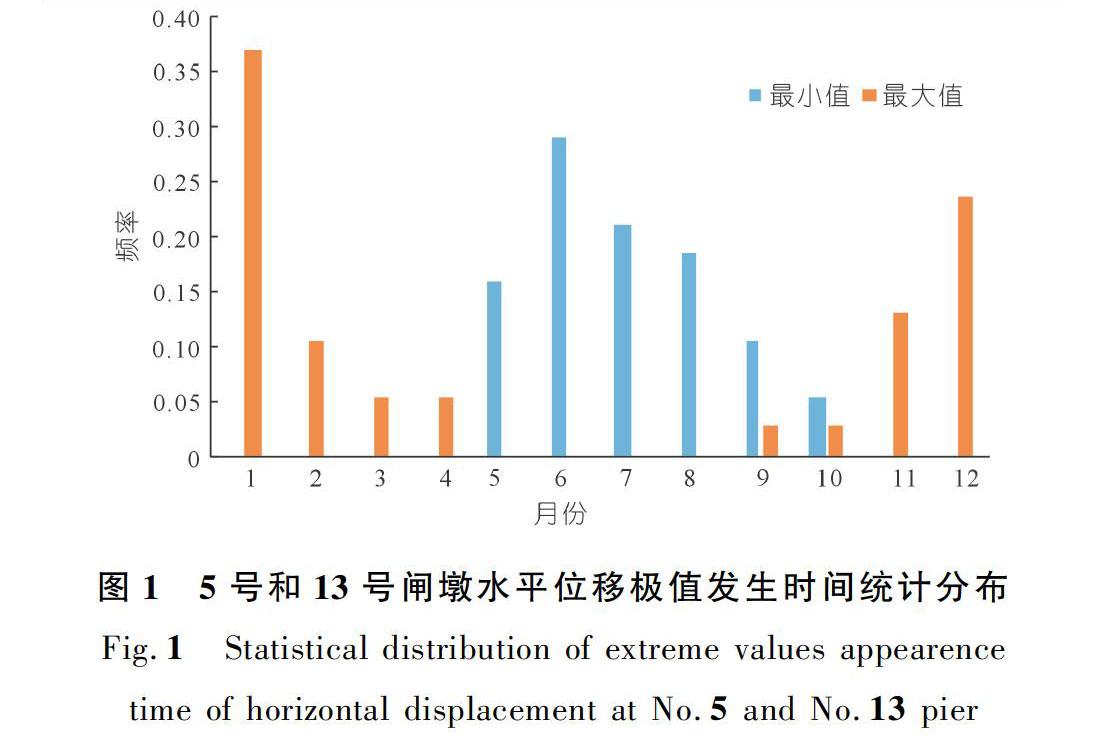
（2） 由最大熵法确定出泄水闸闸墩位移极值的概率密度函数f（x），在此基础上令xm为监测效应量的极值，若当x>xm或x

Pα=P（x>xm）=∫+∞xmf（x）dxP（x

求出随机变量x的概率密度函数f（x）后，估计xm的主要问题是确定失效概率Pα（以下简称α），其值根据大坝重要性确定，一般取1%～5%[8，12]。确定α后，xm由分布函数直接求出：

xm=F-1x，α（5）

2 计算实例

2.1 工程概况

王甫洲水利枢纽位于湖北省老河口市下游約3 km处的汉江干流上，是汉江中下游衔接丹江口水利枢纽的第一个发电航运梯级，以发电为主，结合航运，兼有灌溉、养殖、旅游等综合效益。王甫洲水利枢纽工程等别为Ⅱ等，主要建筑物包括土石坝（含围堤）、泄水闸、电站厂房、重力坝及船闸。泄水闸位于主河道左岸滩地上，泄水闸轴线长413.00 m，共23孔。在泄水闸右边墩（1号闸墩）、左边墩（24号闸墩）之间的 3号、5号、7号、9号、11号、13号、15号、17号、19号、21号、23号等闸墩顶部检修门槽上游侧各布置 1 条引张线，采用人工目测或自动监测的方式进行水平位移监测，规定水平位移向下游为正，向上为负。通过监测获取了2000年7月25日至2018年12月18日近20 a位移监测资料。考虑到每年汛期泄水闸下泄流量较大，因此分别采用K-S检验法和最大熵法确定泄水闸典型闸墩水平位移极值概率密度函数并分别拟定监控指标，对其进行对比。由于王甫洲水利枢纽属于大（2）型水利工程，选取失效概率Pα=1%。

2.2 子样的选择

王甫洲泄水闸闸墩实测水平位移变幅主要受气温变化的影响，且呈现较明显的年周期性变化特征，基本上表现为向上游位移，且在一定的区间内变化。当气温升高时，坝体有向上游变形增大的趋势，而温度降低时坝体向上游变形有减小的趋势。对实测水平位移的最值规定为：实测水平位移数值最小值表示向上游位移最大值，实测水平位移数值最大值表示向上游位移最小值。实测水平位移的最大值和最小值反映了泄水闸极值位移的变化规律，因此将每年的最大、最小位移值作为典型闸墩的计算样本。以泄水闸5号和13号闸墩2000～2018年的位移实测资料作为拟定位移监控指标的资料系列，选取两闸墩每年位移的最大值和最小值作为典型效应量的样本（见表1）。根据对泄水闸水平位移极值发生时间的统计分析，结果表明最大值主要在冬季出现，最小值主要在夏季出现（见图1）。

2.3 监控指标拟定

2.3.1 K-S检验法

利用非参数统计检验K-S法对泄水闸5号和13号闸墩水平位移最小值和最大值的样本数据进行检验，结果如表2所列，可以看出检验结果都满足正态分布。

2.3.2 最大熵法

基于泄水闸5号和13号闸墩水平位移最大值和最小值样本数据，按照最大熵法拟定监控指标的步骤，分别计算其各阶原点矩，结果如表3所列。

确定最大熵概率密度函数f（x）的解析式的关键是求解出满足精度条件的拉格朗日乘子系数λ0、λ1、λ2、λ3和λ4。本文利用單纯形优化算法对拉格朗日乘子系数进行求解。单纯形法[13]计算的基本思路是先在n维空间中取n+1个点构造初始单纯形，比较这n+1个点处目标函数的大小，丢弃最坏的点，以新点代替旧点，不断构成新的单纯形，反复迭代，顶点处的目标函数值逐步下降，直到不断逼近目标函数的最小点即可。通过编写优化计算程序，经计算得到满足精度条件的拉格朗日乘子系数λ0、λ1、λ2、λ3和λ4，进而得到泄水闸5号和13号闸墩水平位移极值最大熵概率密度函数（见表4）。

由K-S法和最大熵法分别获得了泄水闸典型闸墩5号和13号闸墩水平位移最小值和最大值的概率密度函数，再根据式（4）～（5）可分别求得泄水闸5号和13号闸墩水平位移最小值和最大值的监控指标（见表5）。

2.4 对比分析

将采用K-S检验法得到的概率密度函数和由最大熵法计算得到的概率密度函数与实测样本频率进行对比，结果如图2～3所示。

由图2～3可知，由K-S检验法确定的泄水闸典型闸墩水平位移极值概率密度函数基本满足正态分布，该概率密度函数曲线与由最大熵法确定的函数曲线较为接近。对于两种概率密度函数，采用小概率事件法拟定的位移监控指标也较为接近。其中5号闸墩水平位移最大值的实测值为-2.81 mm，超过由K-S检验法拟定的最大值位移监控指标（-2.84 mm），但没有超出由最大熵法拟定的位移监控指标（-2.79 mm）。

3 结 语

以王甫洲水利枢纽为例，采用K-S法和最大熵法确定的泄水闸典型闸墩水平位移极值的概率密度函数曲线较为接近，且拟定的位移监控指标也较为接近，两种方法均可用于监控指标的拟定。

由于王甫洲大坝一直在正常蓄水位附近运行，尚未经历校核洪水位，拟定的位移监控指标为现行不利荷载工况下的极值。后期随着观测时段的不断延长及运行水位的变化，在获得更不利荷载工况时应及时再次拟定位移监控指标。

参考文献：

[1] 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京：河海大学出版社，2006.

[2] 吴中如.水工建筑物安全监控理论及其应用[M].北京：高等教育出版社，2003.

[3] 包腾飞，郑东健，郭海庆.新安江大坝典型坝段坝顶水平位移监控指标的拟定[J].水利水电技术，2003，34（3）：46-49.

[4] 李晓晨，张毅，董龙根，等.典型小概率法在大坝径向位移安全监控指标拟定中的应用[J].三峡大学学报（自然科学版），2014，36（3）：43-45.

[5] 肖云鹏，杨光，刘宴兵，等.一种基于最大熵原理的社交网络用户关系分析模型[J].电子与信息学报，2017，39（4）：778-784.

[6] 胡江，赵冬梅，张旭，等.基于最大熵隐马尔科夫模型的电网故障诊断方法[J].电网技术，2019，43（9）：3368-3375.

[7] 费徐峰，任周桥，楼昭涵，等.基于贝叶斯最大熵和辅助信息的土壤重金属含量空间预测[J].浙江大学学报（农业与生命科学版），2019，45（4）：452-459.

[8] 丛培江，顾冲时，谷艳昌.大坝安全监控指标拟定的最大熵法[J].武汉大学学报（信息科学版），2008（11）：1126-1129.

[9] 马文丽，苏怀智，游艇.基于最大熵理论的大坝安全监控指标[J].水电能源科学，2011，29（6）：77-79.

[10] 殷详详，周钟，赵二峰.基于熵理论的锦屏一级拱坝空间变形预警指标拟定研究[J].长江科学院院报，2016，33（2）：42-47.

[11] 李翔宇，李傲.锦屏一级高拱坝施工期及蓄水期弦长监控指标拟定研究[J].水电能源科学，2015，33（6）：76-79.

[12] 黄耀英，郑宏，周宜红，等.基于小概率事件法估计大坝混凝土实际抗拉强度[J].武汉理工大学学报，2012，34（3）：86-90.

[13] 高立.数值最优化方法[M].北京：北京大学出版社，2014.

（编辑：胡旭东）

Preparation of safety monitoring indicators for sluice pier of Wangfuzhou hydro-junction

YIN Xiaohui1，FEI Dawei1，HUANG Yaoying1，DING Shengyong1，REN Mingxi2

（1.School of Water Resources and Environment，Three Gorges University，Yichang 443002，China; 2.HubeiHanjiangWangfuzhou Hydropower Co.，Ltd，Xiangyang 430048，China）

Abstract：

The preparation of dam safety monitoring indicators can effectively monitor the long-term operation and maintenance of reservoir dams.At present，there are few comparative studies on the monitoring indicators prepared by the maximum entropy method and the traditional classical probability density function method.In this paper，the sluice pier of the Wangfuzhou hydro-junction was taken as an example，and the monitoring data series under adverse load conditions were selected to form small samples.The K-S test method and the maximum entropy method were used to determine the extreme probability density function，and then the small probability event method was used to draft the monitoring indicators.The research results showed that the probability density function of the extreme horizontal displacement of the typical sluice pier determined by the K-S test method basically met the normal distribution，and its probability density function curve was close to the probability density function curve determined by the maximum entropy method.The displacement monitoring indicators prepared by the two probability density functions using the small probability event method were also close.

Key words：

monitoring indicators;sluice pier displacement;maximum entropy method;K-S test method;Wangfuzhou hydro-junction