基于自适应分块的工业机器人压缩感知视觉图像处理

张晓东，苏瑞芳，董唯光

（1.宝鸡职业技术学院 机电信息学院，宝鸡721013；2.兰州交通大学 自动化与电气工程学院，兰州730070）

随着工业4.0 智能制造的发展， 工业机器人发展越来越迅速，机器人视觉系统是机器人的核心组成部分[1]。生产线上，人会因为疲惫作出判断失误和测量错误，但是机器人却能高效稳定的生产，工业机器人视觉系统利用机器代替人眼作出各种测量和判断，但是随着机器人的生产时间增加，需要大量的视觉图像采集存储空间，这就使得数据库容量负担大大增加。为此，需要压缩采样率低、重建恢复效果好、计算效率高的压缩采样算法。

迄今为止，已有部分学者对工业机器人视觉图像压缩问题进行了研究。对于工业机器人而言，传统的视觉图像数据压缩处理方法包括基于信号特征的特征值提取压缩法、多尺度分析的小波压缩法、傅里叶变换的插值压缩法、数据压缩稀化法等[2]，这些方法虽然降低了存储与传输负担，但是这些传统的信号检测与压缩方法仍需具有很高的采样频率，存在着压缩计算复杂、存储空间浪费和适用范围低等问题。由Donoho 和Candes 等人提出的压缩感知（compressed sensing，CS）理论[3-4]，有效地解决了上述问题并指明了新的方向。CS 理论将压缩与采样同时进行，在满足一定条件下通过少量的信号测量值来重构原始信号。该理论降低了模数转换器带宽的要求，取而代之的是信号的稀疏性。稀疏度与信号的重构精度和计算复杂度息息相关，是压缩感知理论应用的前提条件[5]。部分学者将CS 运用在信号处理、谐波检测、图像重构等方面[6-8]。

目前，工业机器人视觉图像信号是一种非线性信号，该视觉图像信号的稀疏性差，导致重构效率低。因此，对于降低工业机器人视觉图像的复杂度及提高重构效率将成为CS 理论研究的关键。文献[9-10]提出了一种自适应视觉图像分块方法，该方法能够自适应地将一个视觉图像分解为若干个小的块分量。对于重构精度和重构速度，文献[11]证明广义匹配追踪（gOMP）算法的重构性能和运行时间优于一般的贪婪重构算法。与gOMP 算法相比，本文研究了利用广义Jaccard 系数的优化gOMP 重构算法具有更好的稀疏性与稳健性。

结合以上2 种思想，本文提出了一种利用自适应分块预处理技术与优化的压缩感知重构算法相结合的工业机器人视觉图像处理方法。利用自适应分块技术把工业机器人视觉图像信号分解为若干个视觉图像块分量，然后对每个块分量图像利用优化的CS 重构算法进行处理， 重构得到工业机器人原始视觉图像信号。与直接采用CS 压缩重构工业机器人视觉图像方法相比，该方法充分利用自适应分块预处理与优化的压缩感知重构算法的优点，不但计算复杂度降低，而且重构精度得到提高。

1 自适应分块预处理的机器人视觉图像

对于大小IM*In个像素的机器人视觉图像X，为体现不同图像内容的纹理结构、边缘特征，并控制分块过程的复杂度，在对工业机器人视觉图像进行稀疏变换之前，以机器人视觉系统图像内相邻像素间的灰度差值表征内容间的相关度，以此作为机器人视觉图像块大小的分割依据，即：

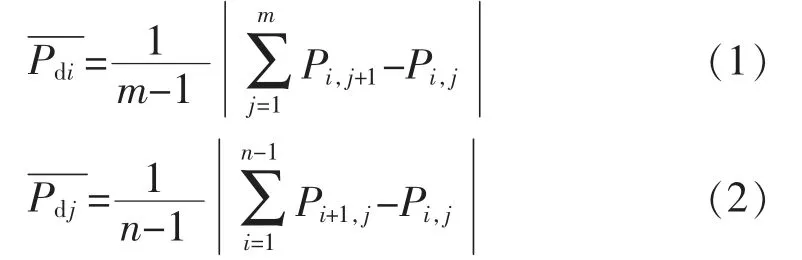
机器人视觉图像自适应分块算法的具体流程如图1所示。利用四叉树算法，即根据机器人视觉图像的纹理变化情况，在需要对视觉图像进一步分割时，将对应视觉图像分成4 个等份的块，从而有效分离平坦区域和细节复杂区域。首先，将图像分成均匀大小的B×B 块，设定分块阈值T，当区域块相邻像素灰度平均差值小于T 时，说明此块机器人视觉图像内容比较平坦，停止分块。为防止相邻机器人视觉图像块边缘出现块效应， 且减小计算量，当块大小分割至4×4 时即停止继续分块。

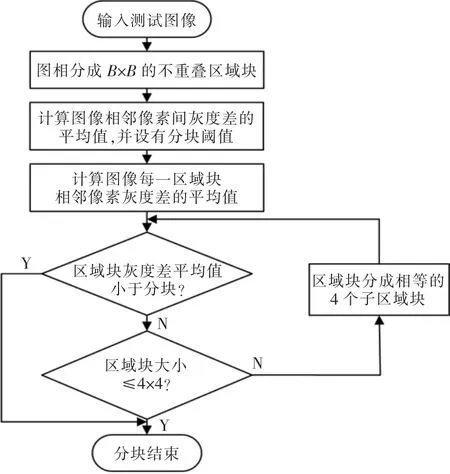
图1 机器人视觉图像自适应分块算法流程Fig.1 Algorithm flow chart of robot vision based on adaptive blocking

机器人视觉图像自适应分块阈值T 由整帧视觉图像相邻像素灰度的行差、列差的平均值决定，即：

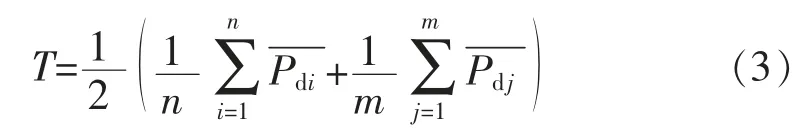
2 优化内积的CS 重建算法

压缩感知理论主要包括信号的稀疏表示，信号的非线性测量表示， 以及信号的重构算法设计，其成立条件是信号是可压缩的或稀疏的[13-14]。

2.1 图像的稀疏变换与测量矩阵设计

将原始有限长一维离散时间实信号X∈RN，可以把信号X= [X（1），X（2），…，X（N）]T在某正交基向量下进行展开，把向量作为列向量转换成字典矩阵ψ=［ψ1，ψ2，…，ψN］，信号X∈RN表示为

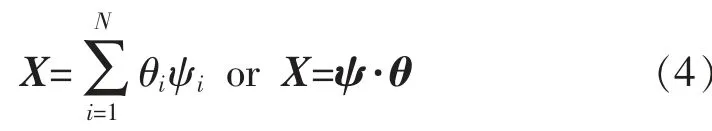
假设稀疏系数向量θ 是K-稀疏的，即向量θ 中非零系数个数K≪N， 取另一个与正交基不相关的测量矩阵Φ∈RM×N（M≪N）对原始信号X 进行压缩测量，得到：

2.2 优化内积的gOMP 重建算法

由于方程（7）属于高度欠定方程，存在无数多组解，但向量θ 是K-稀疏的，从M 个测量向量中可重建θ，即：

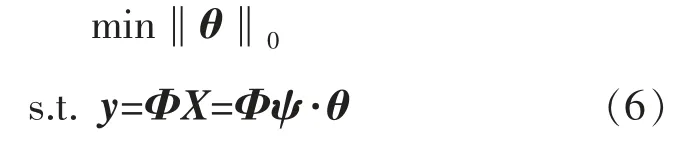
求解该问题典型的重构算法有：正交匹配追踪算法（orthogonal matching pursuit，OMP）、正则化正交匹配追踪算法、分段正交匹配追踪算法、广义正交匹配追踪算法[11]等。

2.2.1 广义正交匹配追踪重建算法

在2012年，韩国高丽大学Wang Jian 等人提出gOMP 算法是OMP 算法的一个改进，该算法每次选择的原子个数大于1（而OMP 算法每次只选择1 个最佳原子）。

算法1gOMP 重构算法

输入：稀疏度K，感知矩阵A=Φψ，投影向量y，S 为≥1 的正整数。

输出：重构信号。

初始化：r0=y，索引集J0≠Ø，A0=Ø，迭代次数t=1。

步骤：

（2）求y=Atθt的最小平方解：

（3）更新残差rt=y-At

（4）如果‖rt-r‖≤ε，进入步骤（5）中运行；否则，令r=rt，t=t+1，跳回步骤（1）中运行；

2.2.2 优化内积的gOMP 重建算法

原始gOMP 算法中，信号代理为

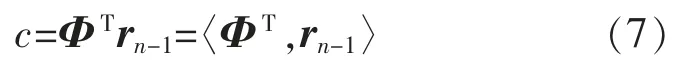
对任意两个向量x，y， 它们的相似度可以用Jaccard 系数来表示[12]：

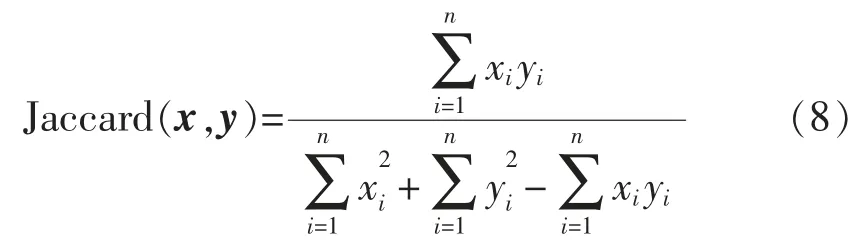
式中：x=（x1，x2，…，xn），y=（y1，y2，…，yn）。

改进的gOMP 使用Jaccard 相似系数作为计算“代理”向量的标准，也就是将式（7）改为式（9）：

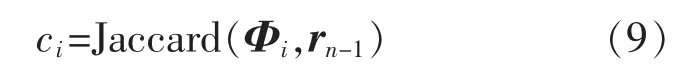
式中：Φi表示Φ的第i 列。

在式（11）中，利用广义Jaccard 相似系数可以充分反映出两个任意向量x，y 之间的相似程度。在计算相似性时，Jaccard 系数把任意两个向量中的各个元素的作用效果放大，主要原因是式（11）分母中减去两个向量中相同的部分， 放大了向量的差异，增大了向量的相似程度， 从而使得原子不容易混淆，具体表现在各个元素对原子的选取，以此优化了支撑集，从而使得重构更加精准，如图2所示。

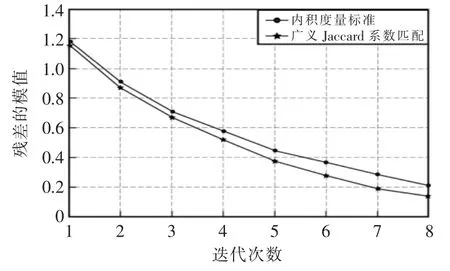
图2 广义Jaccard 系数匹配与内积度量匹配对残差的影响Fig.2 Effect on residuals of generalized Jaccard coefficient matching and inner product matching

3 工业机器人视觉图像压缩与重建的实验方法

本设备由工业机器人、AGV 机器人、托盘流水线、装配流水线、视觉系统和码垛机立体仓库等六大系统组成[13]，如图3所示。

图3 实验室设备组成图Fig.3 Composition diagram of laboratory equipment

通过视觉系统对工件进行识别，然后由工业机器人进行装配，装配完成后，再入库[14]。因此，机器人图像识别与压缩存储是关键，图4为所需要识别抓取和装配的工件。

图4 抓取和装配的工件Fig.4 Workpiece of grab and assemble

采用本文所研究的基于自适应分块预处理的工业机器人压缩感知视觉图像处理示意图如图5所示。

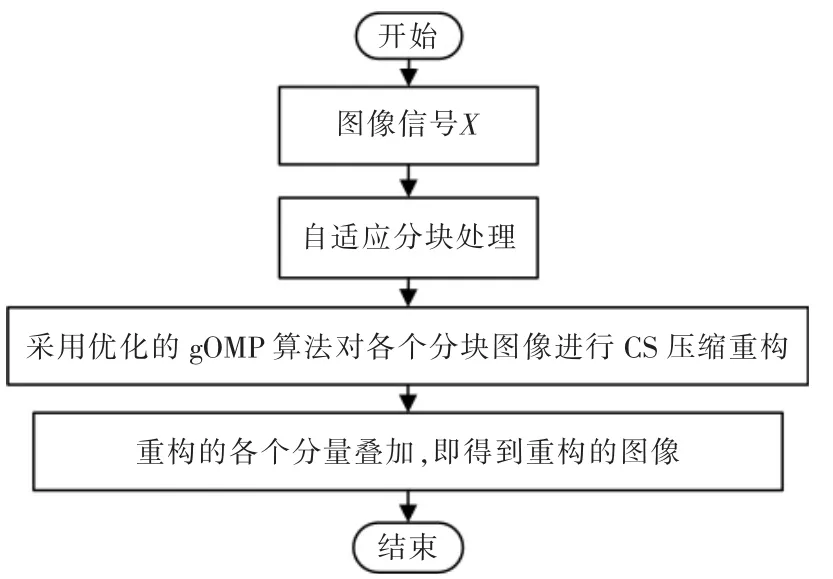
图5 基于自适应分块预处理的工业机器人压缩感知视觉图像处理Fig.5 Industrial robot visual image processing based on adaptive block and compressed sensing

4 实验结果及与分析

本实验在学院工业机器人实验室进行，其中机器人为汇博机器人、电脑参数Windows10 版本，i5CPU 2.7 GHz，4 GB 内存，Matlab2010 上进行。选取一张256×256 的工件图像作为仿真原图像。本文中机器人视觉图像重构质量评价指标为峰值信噪比（peak signal to noise ratio，PSNR）。

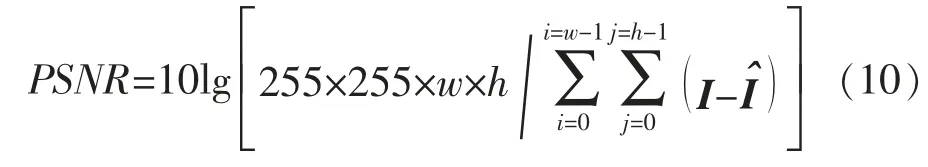
仿真时，首次块大小B 取32，为验证基于工业机器人视觉图像的自适应分块优势，将与均匀分块的效果进行比较。仿真时，均匀块大小分别取8×8，16×16，32×32，基于相邻像素自适应分块的采样率均设置为40%，得到表1、表2的实验结果，图6为自适应分块处理的机器人压缩感知视觉重构图像。

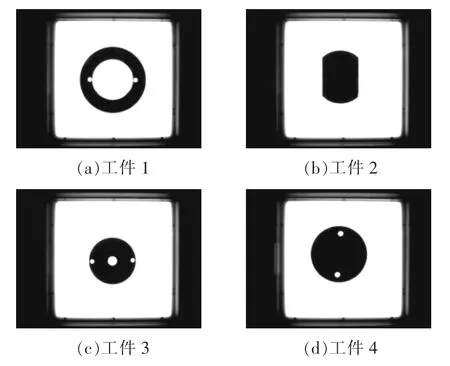
图6 自适应分块预处理的机器人压缩感知视觉重构图像Fig.6 Industrial robot visual reconstruction image based on adaptive block and compressed sensing

对比表1、表2的实验结果可知，采样率相同情况下，相比于均匀分块，基于相邻像素的自适应分块的机器人压缩感知视觉重构方法的重构质量提高2 dB～3 dB，且重构时间缩短40 ms～50 ms。

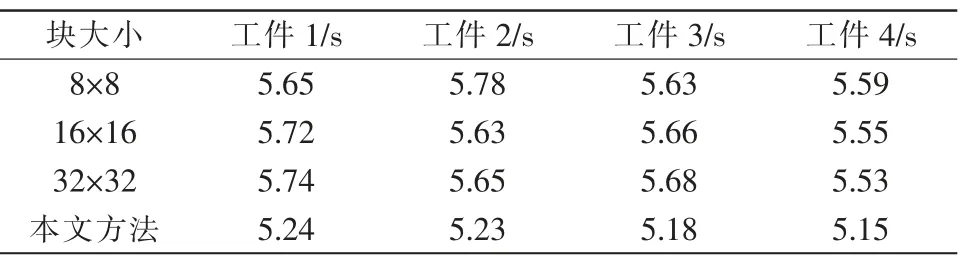
表1 分块的机器人视觉图像重构时间的对比Tab.1 Robot visual image reconstruction time comparison in blocking

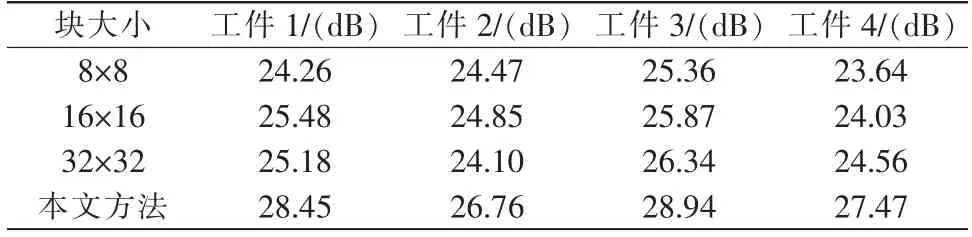
表2 分块的机器人视觉图像重构质量PSNR 的对比Tab.2 Robot visual reconstruction image quality PSNR comparison in blocking

5 结语

本文研究了基于自适应分块处理的工业机器人压缩感知视觉图像处理，利用相邻像素均值为分块依据，本文自适应分块处理的机器人压缩感知视觉重构方法的重构图像质量提高了2 dB～3 dB，且重构时间缩短了40 ms～50 ms，这为工业机器人视觉图像数据存储和图像重构提供新的方法。