基于BAS-BP神经网络的动力电池SOC估算
任舒蕊,王 琪,2
(1.西安工业大学 电子信息工程学院,西安710032;2.西北工业大学 电子信息学院,西安710072)
作为电动汽车电池管理的关键指标,SOC 表示动力电池的剩余电量,这是无法直接测量的状态量,需要使用特定的数学模型或算法进行测量和估计[1-2]。准确估算动力电池SOC,以优化车辆功率分配,可以避免由于电池不一致而导致单个电池过度充电或过度放电,确保整个电池组发挥最大效率[3-4]。
动力电池因其复杂的特性难以创建准确的数学模型,因此大多数学者进行SOC 估算时采用BP 神经网络模型[5]。BP 神经网络拥有非常强大的非线性拟合能力,只是单纯的神经网络在学习过程中收敛缓慢,很容易达到局部最小值[6]。天牛须算法[7](beetle antennae search,BAS)是近几年提出来的一种单体搜索算法,在处理复杂优化问题上有着较高的效率。将天牛须算法(BAS)与BP 网络结合形成BAS-BP 神经网络联合算法用于电池SOC 估算,克服了BP 神经网络容易过分进行数据拟合的缺点,提高了估算的准确性。
基于此,在充分考虑环境温度对动力电池SOC的影响下,本文提出了利用天牛须算法(BAS)改善BP 神经网络,建立BAS-BP 网络预测模型,通过仿真实验比较两种不同模型得出的SOC 值,以此来证明优化算法的准确性。
1 BP 神经网络预测SOC 模型建立
神经网络通常分为3 层结构,即输入层—输入变量数据;输出层—预测输出结构;隐含层—实验数据的权重[8-9]。本文把BP 神经网络的输入向量设置为动力电池的环境温度(T),电压(U),电流(I),输出向量为电池荷电状态SOC,即SOC=f(U,I,T)。BP 神经网络拓扑结构如图1所示。

图1 BP 网络拓扑结构Fig.1 BP network topology
本文中环境温度、电压、电流作为网络的输入,将剩余电量SOC 作为网络的输出层,隐含层节点数量的计算公式为

式中:a 为在[1,10]区间的数值,且根据上式计算可算出隐含层节点数量大于等于3 小于等于12。经过多次仿真实验得到, 网络仿真效果达到最高时,隐含层节点数m=6。
2 BAS 算法优化BP 神经网络
2.1 天牛须算法建模
从嗅觉获取食物的气味强度是天牛须觅食的生物学原理,即当天牛须右侧的食物气味高于左侧时,天牛须会飞向右侧,简而言之天牛须会向食物气味高的一侧飞行[7]。天牛须算法的优势在于天牛须查找不需要知道函数的特定形式,也不需要有效梯度的信息即可进行优化[10-11]。另外,只需要一只天牛来搜索,这大大减少了运算量,天牛须算法简化模型如图2所示。
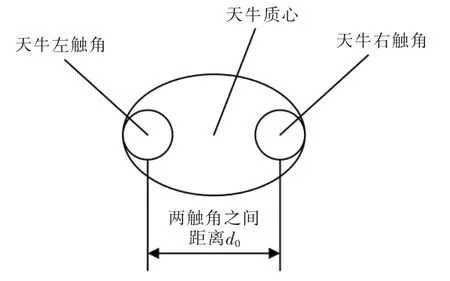
图2 天牛须搜索算法简化模型Fig.2 Simplified model of longhorn whisker search algorithm
天牛须建模步骤如下:
1)建立天牛须行动的任意方向向量:
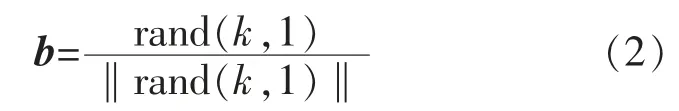
2)创建天牛左、右须空间坐标:

式中:xl,xr分别为天牛须左、右触角位置坐标;d0表示两触角之间的距离;x 为天牛质心坐标。
3)明确天牛两个胡须的味道强弱。通过比较f(xl)和f(xr)的大小来确定天牛行进方向,即
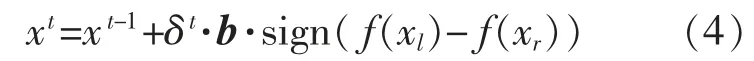
式中:sign()为符号函数;δ 为步长因子。
2.2 BAS-BP 算法
天牛须算法(BAS)的使用具有简单、参数少、计算量少等优点,在处理低维优化目标时具有非常大的优势[12-14],本文将其与BP 网络相结合,创建了BASBP 网络预测模型预测SOC。BAS-BP 算法流程如图3所示。
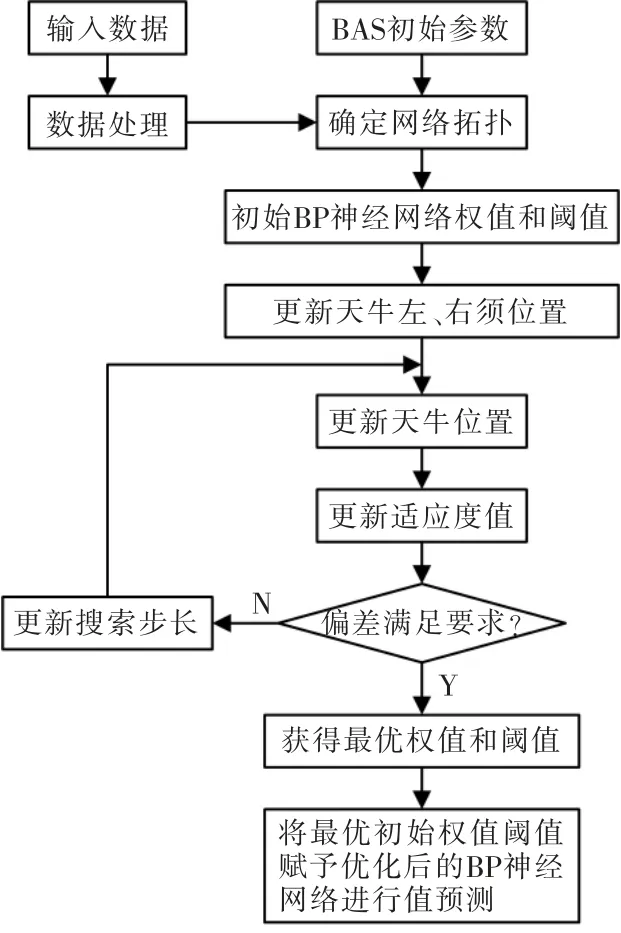
图3 BAS 优化BP 神经网络流程Fig.3 BAS optimizes BP neural network flow chart
BAS-BP 模型建立具体步骤:
1)由BP 网络结构确定空间搜索维度,即优化的粒子个数为
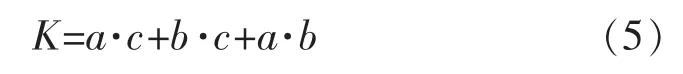
式中:a,b,c 表示输入层、隐含层、输出层中的神经元个数。
2)判断步长因子δ。开始时刻的步长因子不宜太小,容易影响收敛速度。

式中:eta 是接近1 的数字,此处eta=0.8。通过多次实验,确定初始步长为30,初始迭代次数设置为50。
3)确定适应度函数。选择基本测量方法作为平方误差适应性评估函数,适应性函数为

式中:N 为训练样本数;tsim(i)为第i 个样本的模型输出值;yi为样本的实际值。
4)随机设置天牛起始位置,计算它的适应度函数,并存储于bestX(最佳天牛起始位置)和bestY(起始位置的最优适应度函数值)中。
5)将天牛须的空间坐标进行更新,计算出两须之间的适应度函数值进行比较。依据空间坐标更新天牛位置并计算此时位置的函数度适应值。如果它比bsetY 好,则更新bestX 和bsetY。
6)判定适应度函数值是否满足精度要求,或者是否满足最高迭代次数, 其中任一满足时算法终止。这时的权值和阈值为bestX 中的最好的解,将其输入BP 神经网络中,即形成BAS-BP 神经网络模型。
3 实验结果及分析
本文采用18650 三元锂电池,电池的标准电压为3.7 V,充满电的电压为4.2 V,标称容量为2600 mAh。实验前先给电池充满电,然后进行放电试验,在不同的环境温度下(0 ℃,10 ℃,20 ℃,25 ℃)以1 s为间隔采集电池的电压、放电电流以及SOC,用作训练样本估算电池SOC。
3.1 网络训练参数设置
基于天牛须算法参数初始化的原则,经过反复验证计算,本文取eta=0.8;c=5;step=30。本文分别创建了BP 神经网络以及BAS-BP 神经网络,因为训练样本中影响SOC 的因素有3 个,所以网络预测模型的输入节点数为3。隐含层中节点数是按照Kolmogorov 定理选取为6,当m=6 时,优化的权值和阈值个数为31 个,即组成一个31 维的向量。SOC 作为输出层即表示输出节点L=1。本实验中,网络学习次数、学习率、训练目标的误差分别设置为1000,0.01,0.0001。
3.2 BAS-BP 算法验证
对满电量的单节电池进行放电试验,把采集到的所有数据中选取23608 组数据作为BAS-BP 算法的训练集,随机抽取100 组作为测试集。两种模型的预测曲线分别如图4和图5所示。比较图4和图5,我们可以看到优化前的相对误差小于5%,优化后的相对误差小于2%,并且优化后的相对误差显著降低。
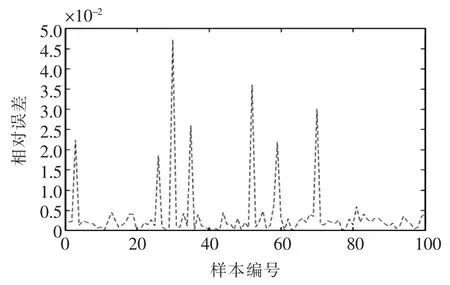
图4 BP 算法预测SOC 误差曲线Fig.4 BP algorithm predicts SOC error curve

图5 BAS-BP 算法预测SOC 误差曲线Fig.5 BAS-BP algorithm predicts SOC error curve
BAS-BP 算法对SOC 真实值与预测值的对比如图6所示。仿真结果显示SOC 的估算值与真实值误差不超过0.9%,决定系数R2=0.00978,仿真结果说明优化后算法估计结果准确。

图6 BAS-BP 算法对SOC 真实值与预测值的对比Fig.6 BAS-BP algorithm compares the true value and the predicted value of SOC
3.3 BAS-BP 性能分析
对BAS-BP 算法的性能[15]进行验证,本文经过MATLAB 仿真实验,阐明优化算法的性能。当m=6时,BP 网络和BAS-BP 迭代曲线训练如图7及图8所示, 当m=6 时,BP 网络和BAS-BP 网络分别经过11次和4 次迭代训练到达目标误差,满足精度要求。
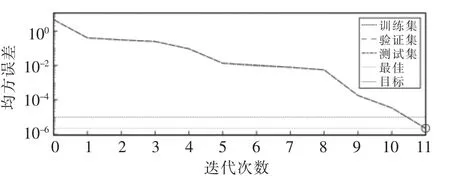
图7 m=6 时BP 网络训练曲线Fig.7 BP network training curve when m=6
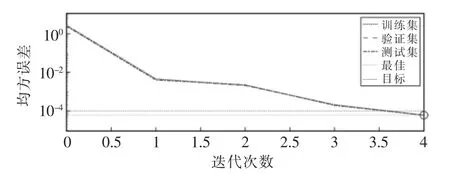
图8 m=6 时BAS-BP 网络训练曲线Fig.8 BAS-BP network training curve when m=6
BP 网络训练结果和BAS-BP 网络训练结果如表1所示。
由表1结果显示,BAS-BP 算法估算SOC 相对误差比BP 算法估算相对误差减小了18.75%,并且优化后的网络训练次数少,网络曲线训练时间提高了13%,说明优化后的网络收敛速度快,能在更短的时间找到最优解,得到更加精确的SOC 估算值。

表1 两种算法训练结果比较Tab.1 Comparison of training results of two algorithms
4 结语
本文在充分考虑环境温度、电池电压、电流对SOC 的影响因素下, 利用天牛须算法优化BP 神经网络结构, 建立了基于BAS-BP 预测动力电池SOC的模型,对SOC 进行估算。实验数据结果显示,SOC估算误差≤2%,收敛速度快,进一步提高了SOC 估算的准确性。

