低应变率范围下花岗岩力学特性研究
偶少龙,暴伟越,孙 策,郭庆飞,姜智彬,吴振宇,郑东平,汤伟雄,邓稀肥
(1.天津大学 建筑工程学院水利工程仿真与安全国家重点实验室,天津,300350;2.中铁建大桥工程局集团第二工程有限公司,广东深圳,518000;3.中铁二十五局集团第五工程有限公司,山东青岛,266000;4.中国电建集团贵阳勘测设计研究院有限公司,贵州贵阳,550081;5.中铁四局集团有限公司,安徽合肥 230023)
引言
岩石的应变速率对岩石的影响是岩石力学领域的一个重要课题,不同的应变速率对岩石的变形以及各种力学特性都有着较大的影响。岩石取芯等资源开采需要较低的开挖速率,对临近岩体的稳定性存在一定的干扰,故低应变率下岩石的力学特性变化值得深入研究。
岩石的应变率效应已有大量研究。黄达等[1]以粗晶大理岩为研究对象,进行了应变率范围在1×10-5~1×10-1s-1的单轴压缩试验,得到起裂和峰值应力随应变率增大而增大的结论,并且发现在1×10-4~1×10-3s-1范围内存在相对反常现象。王进[2]等采用MTS 试验机对红砂岩进行了单轴压缩试验,发现红砂岩的峰值应力、弹性模量与加载率之间呈现良好的正相关关系,而峰值应变与加载率无关。梁卫国等[3]对NaCl 岩盐与无水芒硝盐岩进行10-5~10-3s-1范围内单轴压缩试验,发现二者的强度和弹性模量不随加载应变速率变化而变化,而泊松比随加载应变速率增加而增加。黎强[4]通过不同加载速率下的室内单轴压缩实验,根据破坏后的岩石碎块,计算了不同加载速率下的块度分形维数,发现加载速率与岩石破碎后的块度分布系数呈负相关关系,与加载速率呈正相关关系。迟学海等[5]研究不同加载速率下砂岩碎块的块度分布情况,得到随着加载速率的提高分形维数有增大的趋势,在给定加载范围内分形维数变化区间为2.5~2.7。
现有研究主要集中在1×10-5~1×10-1s-1应变率范围内,更低应变率范围很少涉及,且低应变率下岩石破碎程度的应变率效应研究也较少,因此需要对岩石低应变率内的力学特性变化进行研究。本文利用三轴流变仪对花岗岩进行了 1.5×10-7~4.3×10-6s-1应变率内的单轴压缩试验,分析其力学特性,并且利用筛分对其破碎程度进行研究。低应变率下岩石的力学行为特征的研究,对于工程设计、工程开挖以及工程灾害的防治有着一定的指导意义。
1 试样准备及试验设备
花岗岩试样选取湖北随州的风化花岗岩,密度约为2.60 g/cm3,纵波波速约为3 800 m/s,按照国际岩石力学学会(ISRM)[6]的规定测定了其基本力学参数:岩样的单轴压缩强度约为120 MPa,弹性模量约为31.8 GPa,泊松比约为0.32。为减少岩石原生状态引起试验结果的离散性,试验所用岩样均取自于一块岩芯,并制备成小于常规尺寸的φ25×25 mm 圆柱形试样,以减少岩石试样中结构面存在的概率。
本次试验选用的仪器是河南理工大学的RLW-2000 型岩石三轴流变仪,最大负荷为2 000 kN,测力精度为 ±1 %,位移测量范围0~50 mm,位移精度达到±0.5 %,机架刚度达到500 tf/mm。试验采用位移控制,最终获得1.5×10-7~4.3×10-6s-1应变率范围内的试验结果,力学参数由试验系统进行采集,试样碎片则利用筛网进行筛分称重处理。

图1 花岗岩试样

图2 RLW-2000 型岩石三轴流变仪
2 试验结果分析
2.1 应力应变曲线
图3 为花岗岩6 种不同应变率下单轴压缩试验的应力-应变曲线。低应变率下的应力应变曲线均可以分为压密阶段、弹性变形阶段、微裂隙萌生阶段、微裂隙稳定扩展阶段以及破坏阶段这五个阶段。加载初期,岩石内部的孔隙、裂隙被压密,曲线呈现出上凹状,应力增长速度逐渐加快。当孔隙、裂隙闭合后,岩石进入弹性变形阶段,其应力应变曲线近似为一条直线。随着加载的不断进行,微裂隙萌生扩展至微裂隙不稳定扩展阶段,此阶段应力应变曲线呈上凸状,应力增长速度逐渐减慢至应力达到峰值,最终微裂隙不断扩展贯通形成宏观裂纹,分割岩石导致岩石破坏。

图3 花岗岩试样应力-应变曲线
值得注意的是10-6s-1应变率范围内,花岗岩试样应力应变曲线峰后段均为陡直曲线,而在10-7s-1应变率范围内曲线峰后段较为平缓,且存在阶段特征,即发生应力降。由于岩石的破坏形式为剪切破坏,在较低应变率情况下,局部剪切存在优势面。剪切破坏过程中,剪切段上部沿凸台扩展至特定高度剪断凸台,从而发生应力降,即峰值后宏观裂隙滑移过程中的爬坡啃齿特征[7]。
2.2 力学特性的率效应分析
图4 展示花岗岩的单轴压缩强度与应变率之间的关系,可看出强度与应变率之间呈正相关关系。1.5×10-7~4.3×10-6s-1应变率范围内单轴压缩强度由105.2 MPa 增加至136.1 Mpa,涨幅较大,达到29 %,且强度随应变率的变化幅度逐渐增加。结合已有文献[1]研究,本文采用Logistic 函数进行压缩强度-应变率关系曲线的拟合,从而量化分析压缩强度-应变率之间的关系。
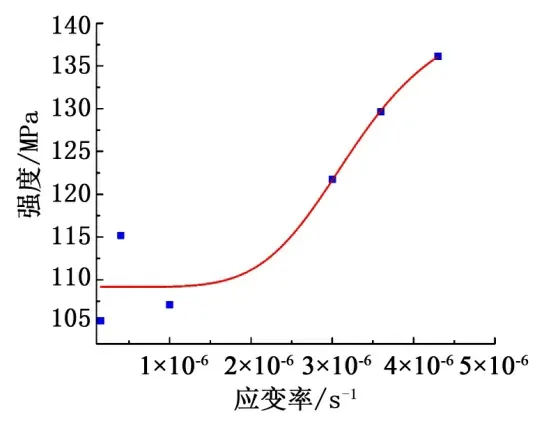
图4 花岗岩试样单轴压缩强度与应变率的关系
Logistic 方程最开始用于形容营养对种群增长的一种线性限制关系,1976 年R.May[8]利用动力学迭代方法在Logistic 方程中发现了混沌,揭示出Logistic 方程蕴藏的丰富内涵。Logistic 方程与混沌学说也广泛应用于岩石领域,张志镇[9]、尹光志[10]、蒋斌松[11]等人均利用Logistic 方程与混沌学说对岩石的损伤、能量进行了研究。本文利用Logistic 函数拟合单轴压缩强度与应变率的关系,结果见下式
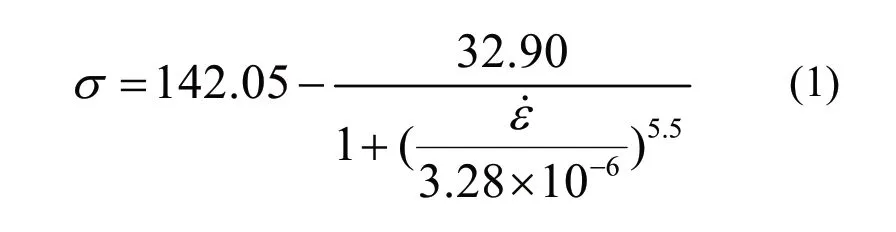
式中:σ为试样的强度,为应变速率。
结果表明,该曲线与函数拟合程度较好,拟合优度为0.926,表面该式在1.5×10-7~4.3×10-6s-1的应变率范围内能够较好的描述二者关系。在该应变率范围内,随着应变率的增加,强度会呈现先缓慢增加,再迅速增加的趋势。在1.5×10-7~1.0×10-6s-1的应变率范围内,花岗岩的颗粒间应力不断转移调整,岩石的裂隙发育程度与初始损伤程度变化幅度较慢,因此岩石的强度较低且变化较慢;随着应变率的增加,花岗岩颗粒间应力难以转移调整,岩石的裂隙发育程度降低,初始损伤程度大大减小,因此强度增长幅度变大。
图5 展示花岗岩的峰值应变与应变率之间的关系,可以看出峰值应变与应变率之间呈负相关关系。峰值应变由0.108 减少至0.083,减少幅度达23 %。随着应变率的升高,裂隙发育时间减短,导致峰值应变减小,表明岩石的变形能力随之减小。
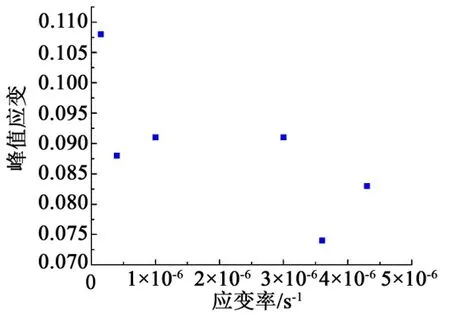
图5 花岗岩试样峰值应变与应变率的关系
图6 展示了花岗岩的弹性模量与应变率之间的关系,可以看出弹性模量与应变率之间呈正相关关系。与压缩强度-应变率变化规律类似,1.5×10-7~4.3×10-6s-1应变率范围内弹性模量由7.1 GPa 增加至11 GPa,涨幅达到55 %。弹性模量与强度整体变化类似,因此采用Logistic 函数进行拟合,拟合结果如下:
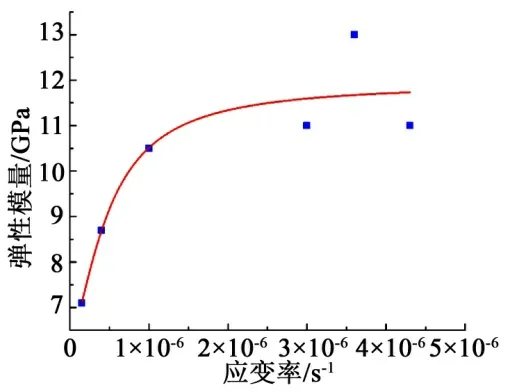
图6 花岗岩试样弹性模量与应变率的关系
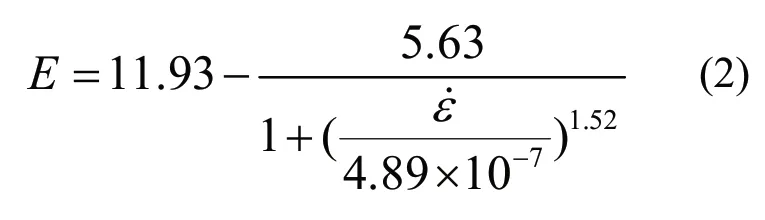
式中:E为试样的弹性模量。
该式在1.5×10-7~4.3×10-6s-1应变率范围内能较好的描述弹性模量与应变率之间的关系。随着应变率的增加,弹性模量会呈现出先迅速增加,再缓慢增加的趋势。弹性模量反映岩石的抗变形能力,在1×10-6~4.3×10-6s-1的应变率范围内花岗岩颗粒间应力难以转移调整,此时的弹性模量只与材料特征相关,故变化不明显。随着应变率的减少,花岗岩的颗粒间应力不断转移调整,导致抗变形能力减弱,因此弹性模量减少幅度较大。
2.3 破碎程度的率效应分析
利用筛径为0.075 mm~25 mm 筛子对试样碎片进行筛分称重,可以得到试样碎片的质量分数-粒径关系,如表1 所示。

表1 试样碎片筛分结果
破碎程度的量化方法很多,例如特征粒径、平均粒径、分形维数等。分形维数以其结果直观,量化精确等优点被广泛应用于岩石破碎程度研究。谢和平院士在1988 年提出将分形几何应用于描述岩石断口的不规则性,并于1996 年将分形几何进行了系统整合和深入研究,将其引入岩石领域[12-13]。分形主要是用于描述微观、宏观的损伤断裂破碎,许金余[14]、杨阳[15]、何满潮[16]等人均利用分形维数对破碎程度进行了相关研究。
根据Tyler 和Wheatcraft[17]提出的公式以及质量分数-粒径分布情况可以进行分形维数的计算
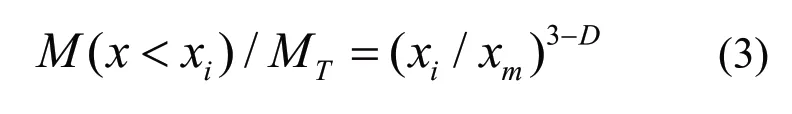
式中:M(x<xi)为粒径小于xi的碎片的累计质量,MT为碎片总质量,xm为最大粒径,D 为分形维数。
该式常用对数形式
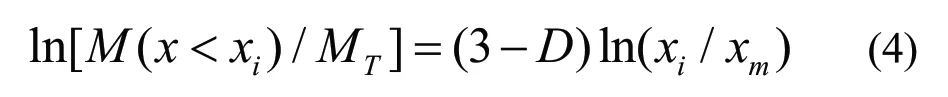
在ln[M(x<xi)/MT]~lnxi双对数坐标轴下进行拟合,拟合得到的曲线斜率为计算的分形维数。拟合结果如表2 所示,该拟合直线的拟合优度均在0.9 以上,说明花岗岩低应变率范围内单轴压缩破坏的破碎程度具有自相似性,符合分形规律,可以采用分形维数来进行描述。
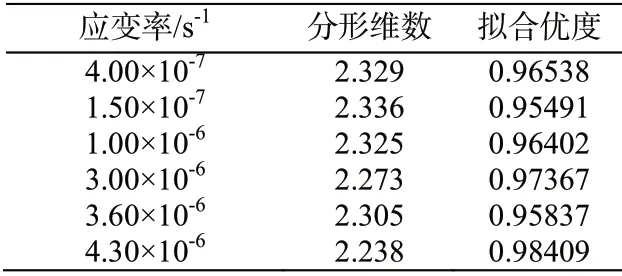
表2 破碎程度分形维数的拟合结果
图7 为分形维数与应变率之间的关系,结果表明分形维数与应变率之间呈现负相关关系。分形维数越大,破碎程度越高,即1.5×10-7~4.3×10-6s-1应变率范围内破碎程度随应变率的增加而降低,与已有1×10-5~1×10-1s-1应变率范围内破碎程度的研究成果不同。原因在于二者的破坏机理有所差异:1×10-5~1×10-1s-1应变率范围内,应变率越大,岩石破坏时间越短,裂隙发育就越不充分,微裂隙越多,破碎程度就越大;而1.5×10-7~4.3×10-6s-1应变率范围内,裂隙发育均较为充分,应变率越低,加载时间越长,裂隙萌生数量越多,破碎程度就越大。与强度、弹性模量与应变率的关系不同,指数函数更适合拟合分形维数与应变率之间的关系。拟合结果如下:
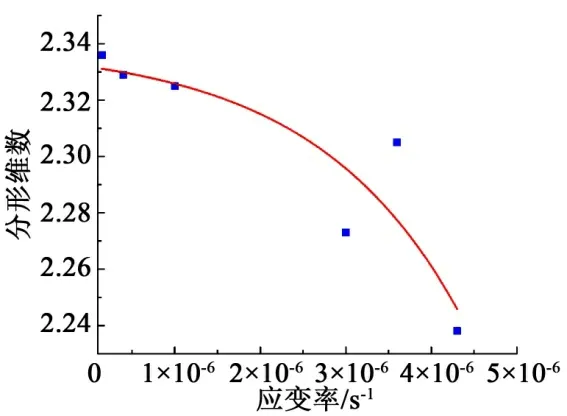
图7 花岗岩试样的分形维数与应变率的关系

该式拟合优度为 0.814,在应变率为1.5×10-7~4.3×10-6s-1的范围内较好的描述分形维数与应变率之间的关系。随着应变率的增加,花岗岩试样的分形维数呈现出迅速减少的趋势,即破碎程度呈现迅速减小的趋势。
花岗岩在低应变率下反映出的力学特性均受到应力转移程度的影响。随着应变率的增加,花岗岩的颗粒间应力转移程度减小,裂隙发育程度减小,初始损伤减小,抗变形能力增强,花岗岩的强度和弹性模量均会增大;应力转移程度减弱,会导致裂隙的萌生数量减少,破碎程度也随之减小。
3 结论
本文利用花岗岩进行了1.5×10-7~4.3×10-6s-1应变率范围内的单轴压缩试验,分析了低应变率对岩石应力应变曲线、强度、弹性模量以及破碎程度的影响,得出以下结论:
1)10-7s-1应变率范围内曲线峰后段较为平缓,且存在阶段特征,存在多个应力降过程,为峰值后宏观裂隙滑移过程中爬坡啃齿的特征所致。
2)花岗岩的压缩强度、弹性模量与应变率之间均呈现正相关关系,而峰值应变与应变率之间呈负相关关系。在1.5×10-7~4.3×10-6s-1应变率范围内,随着应变率的增加,强度会显现出先缓慢增加,再迅速增加的趋势,而弹性模量则会显现出先迅速增加,再缓慢增加的趋势。
3)随着应变率的增大,分形维数在减小,即试样的破碎程度随着应变率增大而减小。1.5×10-7~4.3×10-6s-1应变率范围内,应变率增大,破坏时间减少,导致裂隙萌生数量减少,从而引起试样破碎程度的减小。

