高桩码头变壁厚钢管桩环向焊缝应力集中系数研究
李世亚,向思杰,吴树航,刘佳伟
(1 重庆交通大学,省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074;2 重庆交通大学土木工程学院,重庆 400074)
引言
大型的港工结构受力十分复杂,波浪、风、水流及船舶系缆力等荷载,将会对钢管桩基础产生致命的影响[1],在这些交变荷载循环作用下,钢管桩基础将承受巨大的弯矩作用,导致其焊缝位置处极易产生疲劳破坏。为保证大型海洋工程结构物的安全,焊缝位置处疲劳热点强度研究至关重要,而管节偏位引起的应力集中是影响焊缝疲劳强度的核心因素之一。
钢管桩相比钢筋混凝土桩具有承载能力高、便于调节桩长、施工便利等优势,在各种大型工程中都已广泛运用[2]。钢管桩由钢板热轧焊接而成,钢板被卷成筒状管段(或称管节),为了保证桩的有效长度又能达到节约材料的目的,通常情况下采用壁厚不同的钢管进行连接。但大量实践表明,将二者直接进行横向对接焊接,邻管段之间将产生较大管节偏位,钢管焊接位置处的应力将发生较大突变,形成局部范围内应力集中。相邻管节偏位引起的应力集中降低了焊缝处的强度和韧性[3-4]。为了改善这一状况,常常会在两相邻管段间增设过渡段,即将厚壁段钢管的内侧进行打磨,形成一个斜坡口以便与薄壁段钢管连接,如图1所示。过渡段的设置有助于降低焊缝位置处热点应力,以达到提高焊缝疲劳性能的作用[5-7]。
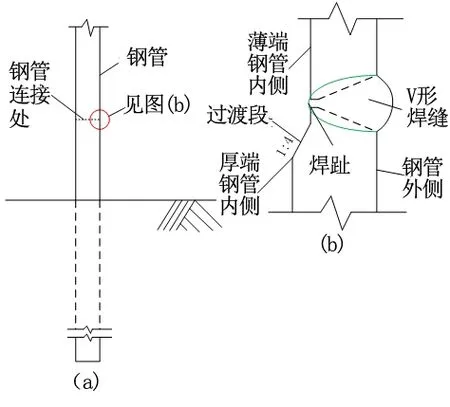
图1 钢管桩焊缝示意图
目前对焊缝处应力集中现象的研究主要是针对焊趾,原因在于,疲劳裂纹通常发生在焊趾处,焊趾位置是疲劳破坏的高发点。因此,获得焊接接头处的应力集中系数有助于进一步掌握焊趾位置的热点应力分布情况,对预测结构疲劳寿命具有重要意义。鉴于此,本文运用数值模拟的方法,探索在弯矩作用下过渡段对焊缝位置处热点应力的影响,并对等壁厚钢管的公式进行修正,为变壁厚钢管环向焊缝设计打下了基础。
1 焊接应力集中的主要理论
在实际工程中,一般采用应力集中系数来描述焊趾位置处热点应力的大小,所谓应力集中系数SCF=σh/σ0,其中σh代表该点位置处的热点应力,σ0代表该点位置处的名义应力,其详细描述可见文献[8]。对应力集中系数求解的理论基础主要分为两类:经典壳理论和平板假设理论,前者虽考虑了管件的环向刚度,计算精度较高[9-10],但主要针对端部无约束的管件[11]且需要明确其边界条件,如焊缝和偏位的具体尺寸,在复杂条件下的实用性有限[12],仅用于轴向荷载作用下的研究。弯矩对焊缝的影响将比轴向荷载更为显著,值得进一步探究。李怡[13-14]通过平板假设理论,推导出了弯矩作用下等壁厚钢管焊缝处应力集中系数的表达式,如下所示。
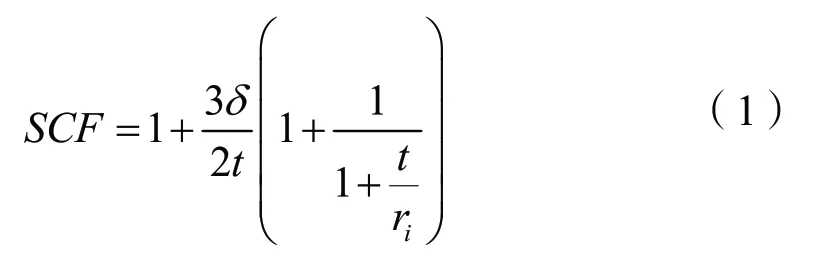
当钢管的壁厚远小于其半径,公式(1)的计算结果与Lotsberg提出的轴向拉力作用下的应力集中系数公式SCF=1+3δ/t[5-6]相同。当钢管的半径ri趋近于零时,即桩身受力以平面弯曲为主,式(1)可转化为李怡等[13-14]提出的计算方法,SCF=1+3δ/2t。其中δ代表管节偏位,t表示钢管的厚度,如图2所示。

图2 等壁厚钢管示意图
从上述分析不难看出,目前对于等壁厚钢管焊缝的研究已较为成熟,但对于变壁厚钢管位置处焊缝热点应力的研究还需进一步扩充。为此齐赵敏、李怡[15-16]对变壁厚钢管桩做了相应的研究,分析了焊缝位置的受力机制,但并未考虑过渡段对焊缝位置热点应力的影响,然而相关文献表明[17-18]在轴力、弯矩等荷载作用下,过渡段可以有效降低热点应力,是影响变壁厚钢管焊缝热点应力一个重要的因素,为此本文仅针对平面内弯矩作用下变壁厚、无端部约束的钢管桩进行数值模拟分析,并通过数值模拟结果对公式(2)进行系数修正,为变壁厚钢管桩焊缝设计提供参考。
2 模型的建立与分析
为直观的分析弯矩作用下变壁厚钢管桩焊缝的应力分布情况,以及过渡段对热点应力的影响。通过数值模拟的方法对焊缝和钢管桩桩身建立三维实体有限元模型,模型一共分为三部分,包括厚管段、薄管段、焊缝。桩身和焊缝的模拟采用实体单元,其弹性模量为210 GPa,泊松比为0.3,钢管的外直径D,取海工钢管桩常见的直径1 m~4 m之间[6],按照0.2 m递增。为了提高计算速度又不失精度,在焊缝位置处网格要适当进行加密,越远离焊缝位置网格越稀疏,此外钢管模型的约束端距焊缝越远,边界约束条件对焊缝应力的影响就越小。综合考虑以上因素,本模型将厚壁段的长度取为钢管外径的4倍,将薄壁段长度取为1 m,综合文献[14]与API RP 2A—WSD中模型厚度的常用取法,两相邻管段之间的厚度T(厚钢管的厚度)、t(薄钢管的厚度)取值分别为25/20、30/25、30/20(mm),两相邻管段间过渡段的长度设置为1.5 cm,过渡段的坡比设置为1:4(即两管壁厚之差比上过渡段长度为1:4,如图1所示)。管壁面网格划分的基本尺寸1mm,网格个数156 320,节点个数406 432,焊缝尺寸的取值主要参照前期的研究成果[[19-20],整体网格模型如图3所示。
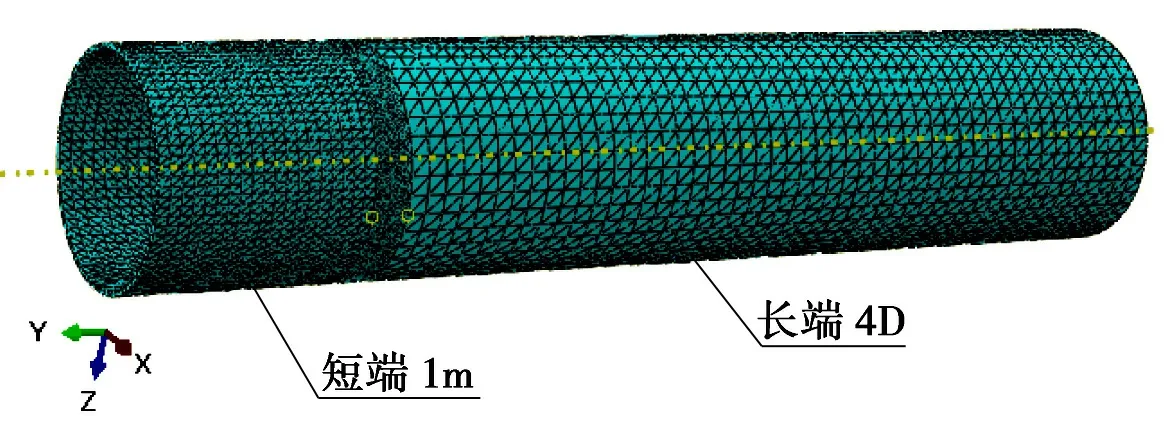
图3 模型网格划分示意图
一般情况下,对大型结构而言,为了保证其可靠性,结构绝大多数考虑为弹性工作状态,故本文在弹性状态下进行研究分析,通过向钢管两自由端施加大小为1 000 kN.m 的弯矩来探究其焊缝位置处的应力集中系数,以达到修正公式(1)的目的,所得结果将用于变壁厚钢管桩焊缝的设计。
3 数值模拟结果分析
数值模拟分析结果如图4 所示,由图4 可知,在弯矩作用下,焊缝位置处出现了较为明显的应力集中现象,最大应力出现在焊趾位置处,达到16.25 MPa。
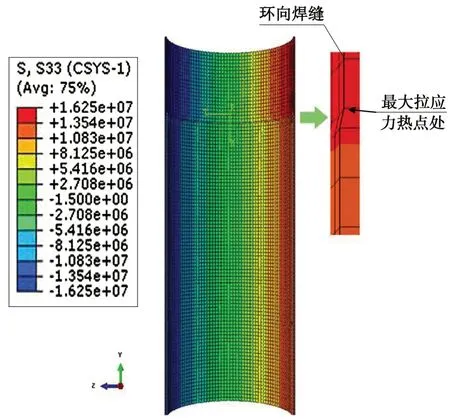
图4 环向焊缝应力云图
将数值模拟结果与公式(1)所得计算结果作比对,可发现数值模拟所得应力集中系数比理论公式结果要小,说明过渡段长度起到了降低应力集中系数的作用,将所得结果绘于表1。

表1 力集中系数对比表
从表1 可较为明显的看出过渡段对应力集中系数的降低幅度与钢管的直径有一定关系,当钢管的直径越大,过渡段对应力集中系数的降低效果就越发明显。当钢管直径在1 m~2.5 m 之间时,模拟值(包含过渡段)大约是计算值(无过渡段)的0.95倍,当钢管直径取2.5 m~4 m 之间时,前者的计算所得的应力集中系数结果大约是后者的0.92 倍。
综上所述,可知过渡段对焊缝位置处热点应力的应力集中系数有降低的效果,且与钢管的直径相关,管直径越大,过渡段对应力集中系数降低的效果就越明显,通过数值模拟的计算结果对等壁厚钢管焊缝位置处的理论计算公式进行修正,给出了相应的修正系数。当钢管的直径在1 m~2.5 m 之间时,其修正系数大约取0.95,当钢管直径取2.5 m~4 m 之间时,修正系数μ=0.92。在未来的设计中对于桩基较小的钢管桩如1 m~2.5 m 时,等壁厚与变壁厚钢管桩焊缝处热点应力集中系数较为接近,则可采用式(1)等壁厚钢管桩热点应力集中系数的公式进行计算,但对于2.5 m~4 m 之间的大直径钢管桩或更大直径的桩,过渡段具有明显降低热点应力的作用,采用式(1)对其计算过于保守,应考虑相应的折减系数μ。
4 结语
1)通过有限元分析发现,过渡段的设置可有效降低钢管位置处的应力集中系数,调节焊缝位置处的应力状态,尤其是对大直径的钢管桩,过渡段对应力集中系数的调节作用将会更加明显。
2)通过数值模拟的方法,考虑过渡段对应力集中系数的影响,对已有的理论公式进行修正,当钢管的直径小于2.5 m,修正系数取0.95,钢管的直径位于2.5 m~4 m 之间时,其修正系数(折减系数)建议取0.92。
3)通过数值模拟的方法,对等壁厚钢管桩焊缝位置处应力集中系数的理论计算公式方法进行修正,针对不同直径的钢管桩,给出了相应的修正系数用于推测变壁厚钢管桩环向焊缝位置处的热点应力,为进一步研究焊趾处裂纹的开裂机理、评估焊接接头的疲劳寿命,了解焊接钢管桩的疲劳破坏性质和探索降低焊缝处应力集中的工程措施提供参考。

