邻近既有地铁的基坑开挖风险评估研究
赵 伟 晋维丽
(北京环安工程检测有限责任公司,北京 100020)
0 引言
随着城市化进程的加快,我国地下空间的开发利用发展迅速,基坑工程紧邻既有地铁施工的现象越来越多,技术难度进一步增大。当建设、勘察、设计、施工或监理单位某些环节出现疏漏时,近接工程[1]的风险就会升高,甚至会造成财产损失和人员伤亡。因此,深入系统地开展基坑近接既有结构物施工安全风险评估研究,对降低该类工程施工安全风险,充分利用地下空间,实现城市和谐可持续发展,具有十分重要的理论意义和实用价值[2]。
国内学者对基坑开挖对邻近既有结构影响和安全性评估进行了深入的研究。黄宏伟从风险管理的角度出发,提出深基坑工程风险管理的一般流程,通过实际案例论证该流程的可行性[3];并通过数值模拟的方法研究基坑工程施工对近接既有隧道的影响[4]。高盟[5]将数值模拟与监测数据结合,研究基坑开挖过程中邻近既有地铁车站的响应,并通过数值模拟讨论分析了控制车站变形施工措施的有效性。
虽然各国学者对近接既有结构施工的基坑工程进行了深入研究,但仍然存在一些局限:1)传统的层次分析法存在一致性不容易满足的局限性;2)缺乏适用于基坑邻近既有地铁施工的风险评估和控制流程,难以实现基坑邻近既有地铁过程中的风险管控。
本文围绕邻近既有地铁的基坑开挖工程进行风险评估,并针对已有研究存在的局限,首先根据数据统计分析法以及对已有研究成果进行风险指标体系的建立;然后应用层次分析法(AHP)与改进的层次分析法(IAHP),分别确定指标层和制约层各风险因素权重;通过模糊综合评判法(FCE)确定项目的风险水平,形成一套针对基坑邻近既有地铁施工方面相对科学实用的风险评估和控制流程;最后结合工程实例,说明该方法的具体应用,为类似工程提供借鉴。
1 AHP与IAHP的对比分析
层次分析法(Analytic Hierarchy Process)简称AHP,最早由美国运筹学家T·L·Saaty于20世纪70年代中期正式提出。由于AHP具有简洁性、实用性和系统性的优势[6],所以在确定复杂问题中诸因素的权重时,AHP被广泛使用。但是AHP也有自身的局限性[7,8]:1)主观因素影响过大;2)当判断矩阵的阶数超过4个时,判断矩阵不容易满足一致性要求。
基于AHP存在的局限性,改进的层次分析法(IAHP)[9]从两方面进行了改进:
一是调查问卷的改进。将处于同一层次的所有因素按重要程度进行排序,可以有效的改善由于判断内容繁杂而产生的厌烦心理,降低主观错误发生的概率;
二是构造判断矩阵方法的改进。IAHP在构造判断矩阵时采用排序赋值的方法,解决了AHP中判断矩阵很难满足一致性的问题。其构造判断矩阵的主要计算步骤如下:
1)确定各层次元素个数,并将该层次元素按照对上层元素的影响程度进行排序;
2)将本层元素对上层元素影响最大的赋值为10,影响最小的赋值为1,其他元素在1~10内线性插值;
3)假定赋值为A,判断矩阵元素值为B,判断矩阵元素按照下面的方法计算:
a.当Ai≥Aj,则Bij=max(Ai-Aj,1);
b.当Ai 虽然IAHP基本解决了各阶判断矩阵的一致性问题,但当判断矩阵阶数小于5个时,由于两种极端情况会同时出现,与实际情况不符,导致按IAHP计算得到的权重准确性会降低,这也是IAHP的局限性。 因此,在实际工程中,为了更准确得出各风险指标的权重,更充分发挥两种方法的优越性,当判断矩阵阶数大于4个时,选择IAHP计算权重;当判断矩阵阶数不大于4个时,选择AHP进行计算。 本文选取某地块基坑开挖邻近既有地铁为研究对象。拟开挖西黄村A-D2地块,该地块位于北京市石景山区,基坑工程自然地面标高64.80 m,基坑开挖深度约18.8 m,基坑长约186.2 m,宽约32.3 m~49.7 m。采用钻孔灌注桩,桩径1.0 m,桩长24.6 m,桩距1.6 m,桩身混凝土强度等级C30。南段基坑西侧采用桩锚支护形式,北侧和西侧采用土钉墙+桩锚支护形式。基坑东半段南侧采用桩锚支护形式,北侧与东侧支护土钉墙+桩锚支护。既有西黄村站为岛式站台,有效站台宽度14 m,车站总长252 m,车站三跨段净宽21.5 m,四跨段净宽30.1 m,高度16.55 m。车站中心里程拱顶覆土约8.5 m,底板埋深约25 m。 根据风险评价指标体系,制约层元素有5个,指标层元素为2个~3个,为了提高各指标权重的准确性,制约层的权重采用IAHP计算,指标层选择AHP进行权重计算。 1)构建制约层判断矩阵。 在此次问卷调查中,调查对象包括与本工程相关的建设单位、勘察单位、设计单位、施工单位以及监理单位中具有高级职称的技术人员,共发放了20份调查问卷并对问卷结果进行汇总,得出制约层的排序和赋值结果,结果表明,施工单位的问题对本基坑工程影响最大,监理单位的问题对本基坑工程影响最小,见表1。 表1 制约层元素排序与赋值 按照表1所示的元素赋值构造制约层B对目标层A的判断矩阵A-B,见表2。 表2 A-B判断矩阵 2)计算制约层判断矩阵对应的最大特征值和特征向量。 本工程判断矩阵对应的特征值λmax和特征向量w的求解步骤如下: (1.134,0.453,1.543,3.471,0.276)。 wa=(wa1,wa2,wa3,wa4,wa5)= (0.165,0.066,0.224,0.505,0.040)。 c.计算对应的最大特征向量λmax,则: 3)检验制约层判断矩阵的一致性。 在计算得到最大特征值和对应的特征向量后,为了证明该特征向量是否为权向量,须进行两步评判,对判断矩阵进行一致性检验。 a.引入一致性指标C.I.进行初判。当C.I.趋近0时,特征向量作为权重向量的可能性较大则认为接近程度很大。 从制约层权重向量中可以看出,施工单位的问题对该近接工程的安全性影响最大,其次是设计单位,监理单位对该工程安全性影响最小;并且该权重与基坑工程事故的统计数据基本一致。 专家依据表2,表3所示的标度含义进行打分,构造指标层C对目标层B的判断矩阵B1-C,B2-C,B3-C,B4-C和B5-C,计算各矩阵权重并进行一致性检验,见表3。 表3 B1-C判断矩阵 则B1-C的最大特征值为2.000,最大特征值对应的特征向量为wb1=(0.250,0.750),由C.I.=0,则判断矩阵一致性满足要求,即B1-C的权向量为wb1=(0.250,0.750)。 按照上述方法计算B2-C,B3-C,B4-C和B5-C判断矩阵并进行一致性检验(过程略)。将本层的几何平均值进行归一化处理,得到指标层所有风险因素的权重,见图1。 从条形图中可以看出:设计时由于设计人员缺乏经验,不遵守设计规范对该工程影响最大,其次施工单位由于施工质量差,随意修改设计图纸而产生的风险也很大,且建设单位由于对价格和工期的压缩可能给其他专业人员带来较大的压力,成为引发冲突和风险的重要因素;勘察单位由于布点过少导致地勘报告数据不全面,给设计单位造成较大的困难;监理如果对发现的问题没有及时的制止或者上报甲方,其监督作用就会丧失,工程的安全性也会降低。 本文采用模糊综合评判法计算该近接工程的风险水平,其基本思路为[9]: 1)建立评价指标的因素集。 因素集主要通过风险评价指标体系确定,其中一级因素集A=(B1,B2,B3,B4,B5)= (业主问题,勘察问题,设计问题,施工问题,监理问题),二级因素集包含2个~3个元素,见表1,表2。 2)建立评价指标的权重集。 制约层和指标层的权重向量已在上节中求得,其中wa=(0.165,0.066,0.224,0.50,0.040),wb1=(0.250,0.750),wb2=(0.833,0.167),wb3=(0.667,0.222,0.111),wb4=(0.582,0.348,0.068 9),wb5=(0.200,0.800)。 3)建立评价等级集和评价等级分数。 评价等级集是专家对评价指标做出评语的集合,这里将评价指标的评语划分为4级[10],即,评语集D=(Ⅳ,Ⅲ,Ⅱ,Ⅰ)=(安全状况很好,安全状况较好,安全状况一般,安全状况不好);再根据相应的工程资料和收集的专家意见,将评价等级集量化,得到该评语集的评价等级分数,即,D=(Ⅳ,Ⅲ,Ⅱ,Ⅰ)=(安全状况很好,安全状况较好,安全状况一般,安全状况不好)=(4,3,2,1)。 4)建立二级评价指标隶属度向量和模糊关系矩阵。 5)进行一级模糊综合评判。应用于本工程中,即: Ei=wbi·Ri(i=1,2,3,4,5),则: 将二级隶属度向量组成二级模糊判断矩阵R,即: R=(E1E2E3E4E5)= 6)进行二级模糊综合评判。将权重向量wa与二级模糊判断矩阵R相乘,得到本工程的综合隶属度向量S,再将综合隶属度向量S与评价等级分数向量D的转置相乘,得到本工程的风险值F,即: S=wa·R=(0.403 0.276 0.204 0.117)。 F=S·DT=2.964。 通过对结果进行分析,本工程的风险值为2.964,属于Ⅲ级风险,属于可接受风险,宜加强工程管理与监测,工程各方应相互配合,采取相应的风险处置措施,尤其是施工单位应提高施工质量,设计单位应严格按照设计规范进行设计,保证施工安全。 1)本次将涉及到邻近既有地铁施工的基坑工程模糊性、不确定性的风险因素进行量化处理,得出基坑施工的问题对该工程的安全性影响最大,其次是设计单位,与基坑工程事故的统计数据基本一致;并且风险在可接受范围之内,可采取相应的风险处理措施; 2)当判断矩阵阶数大于4个时,选择IAHP计算权重;当判断矩阵阶数不大于4个时,选择AHP进行计算,能解决一致性不容易满足的局限性,并且可以发挥各方法简洁、实用且系统性的优势,可为类似工程提供借鉴。2 案例分析
2.1 工程概况
2.2 由IAHP确定制约层权重

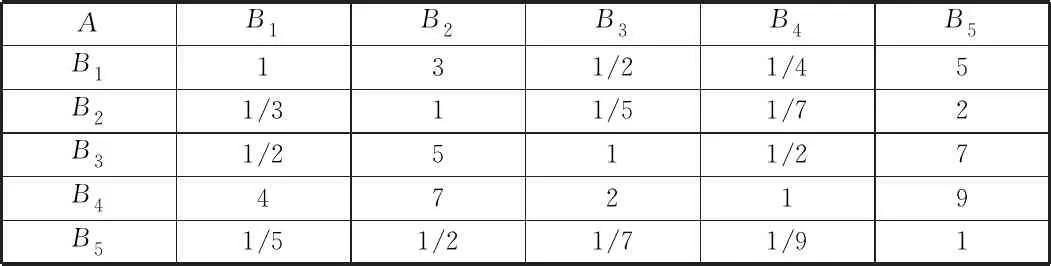
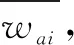
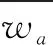
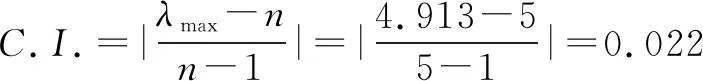

2.3 由AHP确定指标层权重


2.4 风险水平的确定

3 结论

