基于Fe-safe软件的转叶式舵机疲劳分析及优化建议

韦红钱 倪培源 端传捷

（1.南京中船绿洲机器有限公司，南京 210000；2.河海大学 港口海岸与近海工程学院，南京 210000）

船舶舵机是重要的船舶操纵设备，其性能直接影响船舶的稳定性和安全性。随着船舶制造业的飞速发展，船舶吨位越来越大，对舵机的要求越来越高。转叶式舵机与其他舵机相比，具有结构紧凑、质量小、体积小、安装方便、维护简便、输出扭矩不受转舵角的影响以及控制性能好等优点[1]，因此一直备受人们的关注。

1 工作内容

计算内容包括产生疲劳裂纹的部位、产生疲劳裂纹的时间、工作应力作用下的安全因子及存活概率。输出结果包括疲劳寿命分布、疲劳损伤分布、应力/应变时程以及裂纹方向等[2]。

Fe-safe作为一款疲劳分析软件，计算前需要其他求解器的求解结果，如abaqus中的.fil文件和.odb文件、ansys中的.rst文件以及nastran中的op2文件等。将求解结果导入Fe-safe后建立载荷的时间历程、材料及对应的S-N曲线，并定义表面粗糙度和算法等相关参数。计算后得到某一点处的循环周次，通过其他后处理软件读取相应的可视化结果。

2 舵机数值模型建立

舵机由缸体、缸盖、静叶、转子、衬套、盖板、推力轴承及螺栓等零件组成[3]。其中：螺栓1为连接缸盖与缸体的36个12.9级螺栓；螺栓2为连接缸盖与静叶的6个8.8级螺栓；螺栓3为连接缸体与静叶的6个8.8级螺栓；螺栓4为侧面缸体与静叶的12个8.8级螺栓，如图1所示。缸体、缸盖及静叶的材料为球墨铸铁QT400-18，弹性模量为173 GPa，屈服强度为250 MPa；转子的材料为球墨铸铁QT400，屈服强度为335 MPa；螺栓均采用45号合金钢，弹性模量均为210 GPa；上下盖板为Q235钢；上述材料的泊松比均取0.3。

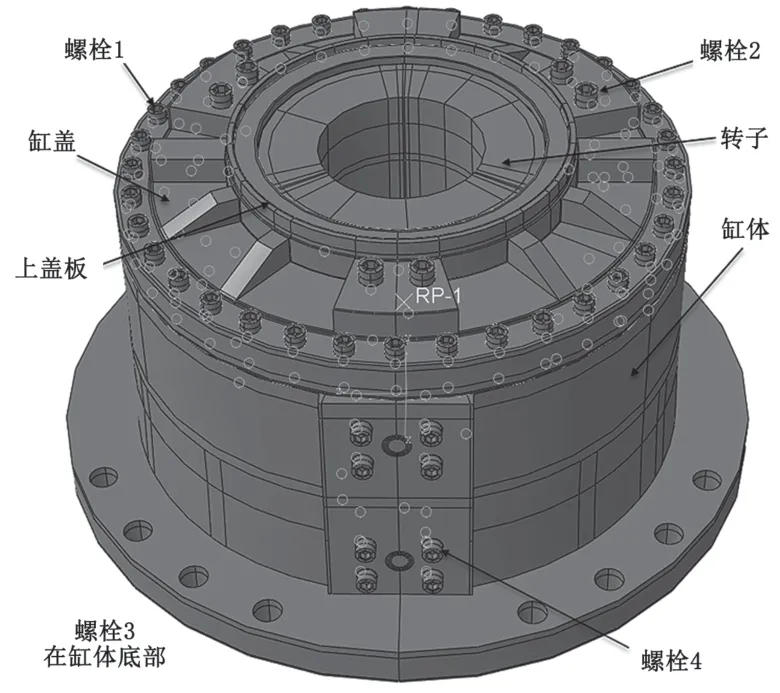
图1 舵机整体模型示意图

舵机各个部件表面的接触关系可以分为摩擦接触和绑定接触两类。摩擦接触关系的表面主要包括螺栓1螺母底面与缸盖顶面、螺栓2螺母底面与缸盖加劲板的顶面、螺栓3螺母底面与缸体底加劲板顶面、螺栓4螺母底面与缸体、缸盖部分底面与缸体顶面；绑定接触关系的表面主要包括螺栓1螺杆侧面与缸体螺孔内侧面、螺栓2、3、4螺杆侧面与静叶螺孔内侧面、上压盖与缸盖的接触表面、下压盖与缸体的接触表面。本舵机模型采用六面体网格，单元类型为非协调八节点六面体单元。螺栓上存在预紧力，螺栓1上为 240 kN，螺栓2与螺栓3上为260 kN，螺栓4上为180 kN。

3 基于Fe-safe软件的舵机部件疲劳寿命分析

3.1 影响疲劳的因素

影响疲劳的因素主要包括：①平均应力，平均应力越大，寿命越低，当平均应力为拉应力时，也是如此；②应力分布方式，高应力区较多的构件（如大直径构件）更容易破坏；③载荷作用方式，如拉压比弯曲更容易破坏；④构件表面因素，如表面光洁度等[4]。

3.2 Fe-safe软件疲劳寿命计算方法

实际产品在工作过程中处于多轴应力状态，且疲劳破坏都从构件表面开始。构件表面在多数情况下处于二向应力和三向应变状态。因此，Fe-safe软件更多地采用二轴分析方法，对构件进行力变-疲劳分析计算。Fe-safe推荐使用的疲劳裂纹产生条件，对延性金属采用平均应力修正的Brown-Miller组合应变准则。该准则认为最大疲劳损伤发生于经受最大剪应变幅的平面，且损伤与该平面上作用的剪应变和正应变有关，对延性材料能提供较佳的计算结果。

由最大主应变准则和最大剪应变准则可假定：

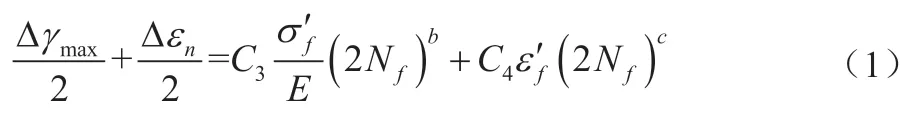
式中：Δεn为最大/最小剪应变平面上的正应变幅；Δγmax为最大剪应幅；2Nf为转变寿命；σ´f为疲劳强度系数；ε´f为疲劳延性系数；b为疲劳强度指数；c为疲劳延性指数；E为弹性模量；C3、C4为系数。

对单轴应力有：

式中：ε1、ε2为主应变；ν为泊松比。

从而，有：

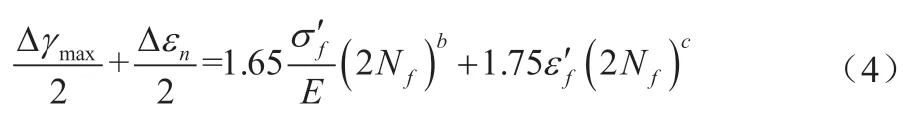
计算确定构件表面最容易出现疲劳破坏的平面和方向，也称为临界平面法。对主应力/主应变方向随载荷历程变化的情况，因很难确定哪个平面的应变循环范围和循环次数最大，应采用临界平面分析法计算一系列平面的应变和损伤，常用于主应变/主应力方向随时间变化情况下的主应变/ 主应力、最大剪应变以及Brown-Miller疲劳寿命分析。

考虑平均应力的影响后，式（4）修正为：

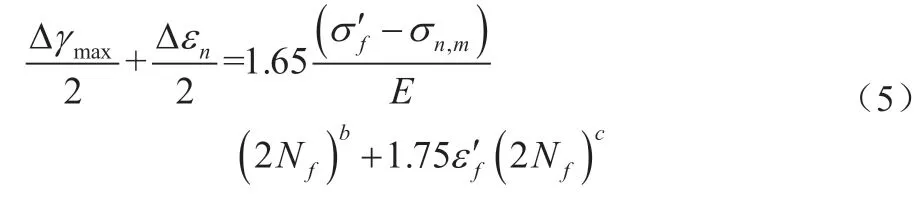
式中：σn,m为该平面上的平均正应力。

3.3 Fe-safe软件疲劳寿命计算步骤

第一，读入弹性计算的FEA应力张量（6个），用载荷历程数据乘以应力张量，得到每个张量的历程数据。第二，计算表面主应力的时间历程（对接触则考虑面外应力），从应力计算3个主应变的时间历程数据。第三，采用临界平面法，分析剪应变和Brown-Miller，在3个可能的平面上计算剪应变、法向应变、法向应力的时间历程数据。第四，分析S-N曲线，定义一个临界平面，计算垂直于该平面的时间历程应力数据。第五，计算每个临界平面的疲劳损伤，各平面的每种疲劳循环用雨流计数法统计，总损伤由每种循环的损伤叠加而成。具有最短寿命的平面即为裂纹发生平面，将其寿命写入结果文件。第六，修正耐劳极限，如果临界平面内的各种循环均低于耐劳极限，则没有损伤产生。如果任一循环有损伤产生，则自动将耐劳极限降低25%。损伤曲线基于修正后的耐劳极限估算。此外，对每个单元都重复上述过程。

3.4 材料S-N曲线定义

采用S-N曲线计算该舵机的疲劳寿命，舵机主体材料为球墨铸铁QT400-18，与欧盟材料牌号为EN-GJS- 400-18的球铁力学性能基本一致[1]，这里使用该材料的S-N曲线近似代替QT400 -18材料，对于螺栓、衬套、轴承及压盖在Total Material官网上查得其近似材料的S-N曲线。各材料使用的疲劳曲线分别如图2～图6所示，各曲线中的数据均具有97.7%的可靠度，其中循环次数的安全系数取5，应力范围的安全系数取1.3。

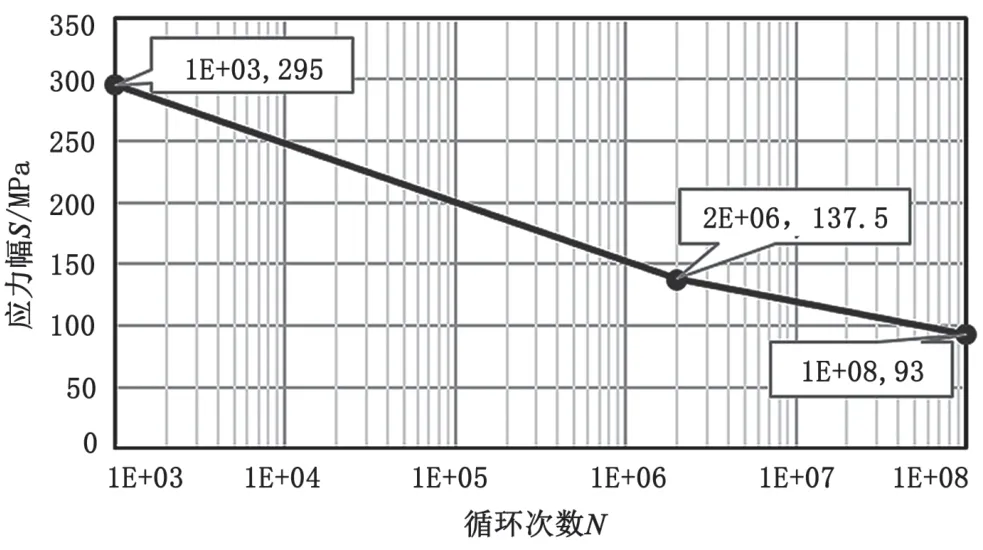
图2 QT400-18疲劳曲线

图3 12.9级螺栓合金钢疲劳曲线

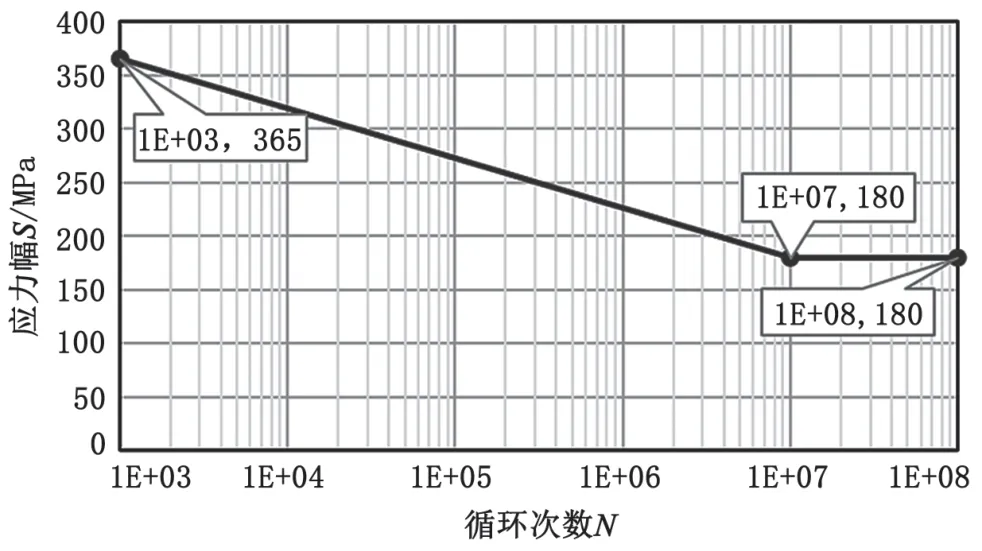
图6 压盖Q235-A疲劳曲线

图4 销轴、8.8级螺栓合金钢疲劳曲线

图5 轴承ZCuAl10Fe3Mn2疲劳曲线

3.5疲劳荷载

舵机工作过程中，高压腔与低压腔循环交替。缸体、缸盖、静叶及转子的受力面一直处于变化中，难以直接定义疲劳载荷。静力分析也是对舵机整体进行的，由于存在较多的接触问题，也难以简单地对每个部件进行单独分析（转子除外）。因此，这里对除去转子的舵机整体进行疲劳分析，转子单独分析。这里疲劳分析的有限元网格进行了局部加密，静力分析总单元数约为25万，疲劳分析的单元数约为60万。由于载荷的方向、位置一直处于变化中，疲劳载荷不能简单地用正弦曲线等来定义，这里按下述方法来定义。如图7所示，这里主要的分析工况为：转叶中心线左转12°各节点的表面应力为s1，初始0°位置各节点的表面应力为s2，转叶中心线右转12°各节点的表面应力为s3，初始0°位置各节点的表面应力为s4，转叶中心线左转12°各节点的表面应力为s5。每个节点由s1→s2→s3→s4→s5→s1组成的应力谱即为特定工况下的疲劳载荷谱，对应的工作压强为3 MPa，周期为18.4 s。

图7 舵机疲劳工况

4 Fe-safe软件疲劳寿命计算结果及分析

主要零部件的对数疲劳寿命（即logN）分布及疲劳安全因子分布结果如图8～图11所示。

图8 除缸体外舵机对数疲劳寿命分布

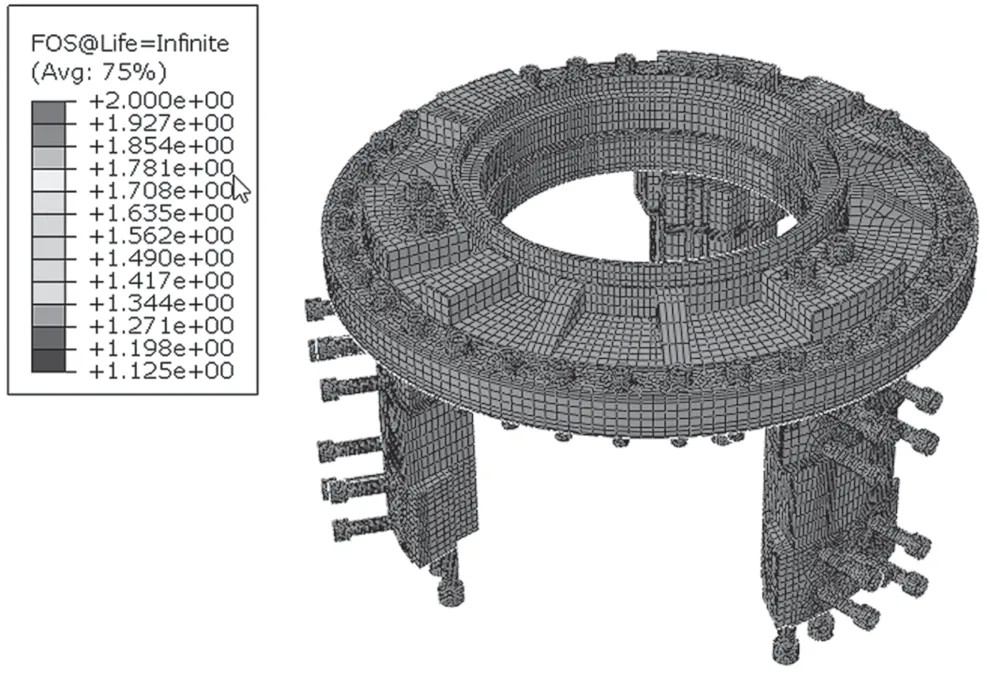
图9 除缸体外舵机对数疲劳安全因子分布

从图8～图11可以看出，在3 MPa的工作压强下，除缸体外所有部件疲劳寿命达到了耐劳极限值108次，缸体的疲劳寿命为106.992=9.82×106次。假定舵机每天工作24 h，一年按365天计算，最终算得缸体部分最小疲劳寿命约为81年，超过了舵机的设计使用寿命30年。S-N曲线计算得到的寿命一般为全寿命。对于纯机械疲劳，裂纹萌生寿命一般在总寿命中占比约90%[2]，裂纹扩展寿命相对很短，因而最小裂纹萌生寿命为72.9年，大于设计寿命30年。实际在使用过程中，舵机尚未出现过裂纹，理论上在设计使用年限里不会出现裂纹，因此这里可不进行断裂分析。

图10 缸体对数疲劳寿命分布

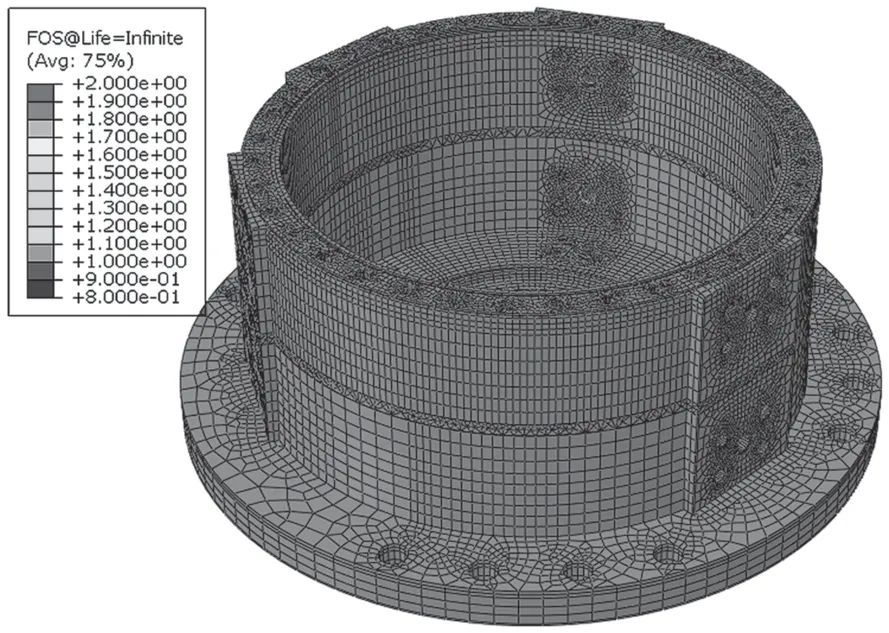
图11 缸体对数疲劳安全因子分布

当作用的载荷幅低于某容许值时，构件不会产生疲劳破坏，将该容许值称为构件的耐劳极限幅值。对于钢材，一般以107次为失效循环允许的载荷施加次数。这里舵机整体以QT400-18球墨铸铁为主，材料的综合性能与钢接近，因而可近似取其疲劳寿命为107次。对于极其重要的零件设计，一般控制应力S，使其小于无限寿命（Nf=106）对应的耐劳极限Sf，该种疲劳设计方法称为无限寿命设计。该设计方法的构件应力水平要求很低，无法充分发挥材料潜力，对于并不需要经受很多循环次数的构件，经济性较低。

5 结语

本研究基于S-N曲线，采用Fe-safe软件分别分析了800 kN·m转叶式舵机各个部件的疲劳寿命。结果表明，所有部件的疲劳寿命均超过了设计使用寿命，属于无限寿命设计，无法充分发挥材料的潜力，对于并不需要经受很多循环次数的构件，经济性较低，可进一步考虑密封条和温度的影响，通过优化设计，在不影响使用寿命的前提下进一步优化舵机结构。