非圆齿轮数控滚齿加工误差PID控制仿真研究
胡闪闪 夏 链
(合肥工业大学,合肥 230009)
滚齿作为一种常见且高效的加工方式,可以加工常规齿轮和非圆齿轮[1-2]。但是,受导轨直线度误差、滚珠丝杠反向间隙、刀具磨损、刀具受热受力变形以及系统控制误差等多种因素影响,齿轮轮廓容易产生误差[3-7]。近年来,非圆齿轮以自身诸多的优点[8]获得了进一步发展,但存在加工精度不高的问题。非圆齿轮数控滚切加工是由多个运动轴联动实现的。由于非圆齿轮节曲线是非圆形,导致各轴频繁加减速,易引起机床振动、切削力突变等现象,进一步降低了非圆齿轮齿面加工精度。但是,随着机床运行速度的不断提高,机床运动控制误差将会成为影响非圆齿轮加工精度更大的一个因素。
目前,滚齿加工机床各运动轴控制多采用比例-积分-导数控制器(Proportional Integral Derivative,PID),可以通过人工手动调节PID控制器参数。为了减少调节时间和获得更好的PID控制参数,通过粒子群优化算法对数控滚齿机存在较大跟踪误差的工件轴C轴和径向进给轴X轴的PID控制器参数进行优化,将优化结果输入控制模型进行仿真验证,实现了减少跟踪误差的目的。仿真结果表明,采用粒子群算法优化带前馈的PID控制是可行的。
1 非圆齿轮滚齿加工
1.1 非圆齿轮滚齿加工模型
根据直齿非圆齿轮齿廓形成原理,直齿非圆齿轮滚齿加工运动关系主要包括展成运动、径向进给运动和轴向进给运动,如图1所示。其中:展成运动(范成运动)即工作台(C轴)按照滚刀与毛坯之间的啮合关系跟随主轴(B轴)做回转运动,并且保证在变速比条件下滚刀与工件回转中心之间的距离随时变化;径向进给运动即滚刀根据工件极径变化产生的径向往复运动(X轴),完成中心距变动;轴向进给运动即滚刀沿着工件轴向(Z轴)的走刀运动。
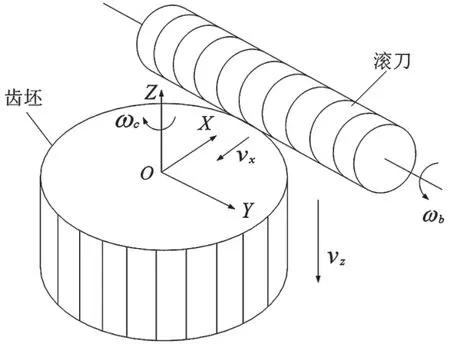
图1 直齿非圆齿轮加工原理图
1.2 建立直齿非圆齿轮数控滚齿电子齿轮箱结构模型
直齿非圆齿轮滚切加工时,滚刀回转运动作主运动,工件回转运动与径向进给运动作跟随运动。
滚刀与工件之间的运动关系为:
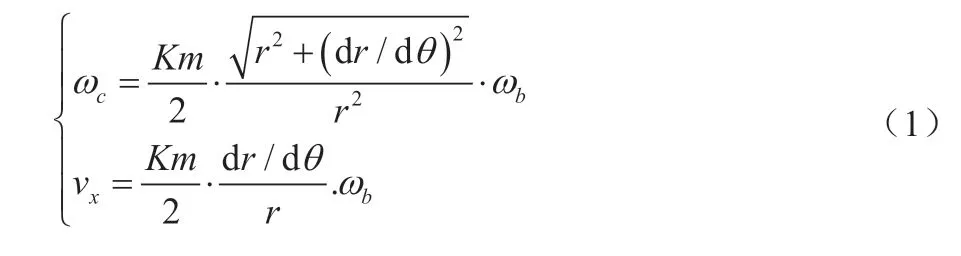
式中:ωb为滚刀转速;ωc为工件转速;vx为滚刀沿齿坯轴径向进给的速度;r为节曲线极径;θ为节曲线极角;k为滚刀头数;m为模数。
在每个插补周期中,电子齿轮箱(Electronic Gear Box, EGB)[9]模块根据主轴B轴编码器的反馈信号与非圆齿轮多轴联动控制数学模型,实时计算工件回转轴移动增量Δθc与径向进给移动增量Δx,实现主从同步控制。其中,径向进给移动增量Δx的值由电子齿轮箱计算结果和工艺参数得出,轴向进给移动增量Δz的值从通用插补执行模块读取,如图2所示。
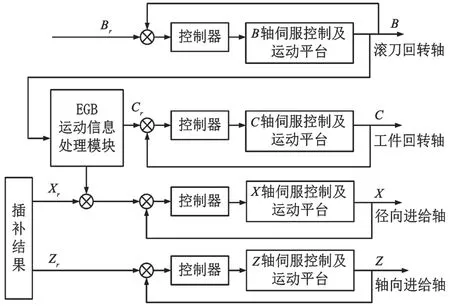
图2 直齿非圆齿轮数控滚齿电子齿轮箱结构模型
2 伺服控制系统建模
在伺服控制系统中,传统的PID反馈控制可以让外界干扰、参数变化等现象对系统有较小的影响,但在非线性轮廓控制中跟踪性能较差会产生较大的轮廓误差。为了提高伺服跟踪性能,使输出指令快速地跟踪输入指令,引入前馈控制对未来信息进行判断,拓宽系统频带。所以,采用反馈与前馈相结合的控制方式,即能降低反馈控制带来的跟踪滞后,又能对偏差进行及时校正补偿,从而改善伺服跟踪性能。
图3中:R(s)、Y(s)分别为系统的输入和输出信号;E(s)为系统输入和输出信号之间的偏差;P(s)为被控对象的传递函数;G(s)为PID控制器传递函数;F(s)为前馈环节的传递函数。

图3 单轴复合控制原理图
系统误差传递函数为:

为实现系统偏差值为0,则输入信号等于输出信号,即E(s)=0、R(s)=Y(s),系统前馈环节传递函数F(s)满足F(s)=1/P(s)。
将前馈环节传递函数F(s)展开成s的级数:
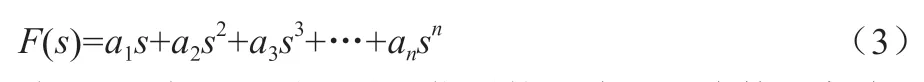
式(3)表明,需要引入位置的一阶、二阶甚至高阶导数才能完全消除跟踪误差,但实际控制系统由于是非线性的且线性范围有限,在很大定程度上增加了设计高阶微分器的难度。此外,微分阶数越大,输入噪声的敏感度将会更明显地影响到实际控制系统,导致工作性能降低。因此,从实际应用角度来说,通常微分阶次为二阶时,控制效果较好。
速度前馈补偿指的是指令位置的一阶导数乘上相应增益系数叠加到速度控制指令中,可提高系统的响应速度。加速度前馈补偿指的是取指令位置的二阶导数乘上相应增益系数叠加到加速度控制指令中,能够有效抑制速度前馈产生的超调。本文对跟踪误差波动较大的工件轴C轴和径向进给轴X轴,均采用“速度/加速度前馈+PID/PI”的伺服控制模型,如图4所示。

图4 “速度/加速度前馈+PID/PI”控制模型
3 粒子群优化算法
3.1 粒子群算法及优化原理
粒子群算法(Particle Swarm Optimization,PSO)[10]是研究鸟群迁徙觅食行为的一种智能的全局优化算法,最早由Kennedy博士和Eberhart教授于1995年提出。算法中,每个粒子相当于鸟群中的鸟(潜在解),通常采用3项指标(位置、速度及适应度值)来表示粒子状态是否有效。在搜索区间粒子进行寻优时,通过得到的适应度值更新个体极值Pbest和群体极值Gbest,并对个体的位置和速度进行更新。
根据粒子群算法和优化原理,粒子自身速度和位置更新公式为:
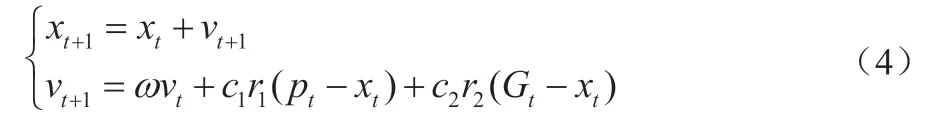
式中:xt、xt+1分别为粒子第t、t+1次迭代时的位置;vt、vt+1分别为粒子第t、t+1次迭代时的速度;ω为惯性权重;c1、c2为加速常数;r1、r2为[0,1]上的随机数;Pt为粒子当前的最优位置;Gt为整个粒子群的最优位置。
3.2 性能指标
在粒子群算法中,以适应度值的好坏来评价该粒子的优劣。在控制工程领域中,常用的时间乘以误差绝对值积分(Integrated Time Absolute Error,ITAE)指标在实际应用中可实现对系统动静态性能的综合评价[11]。因此,本文选择ITAE作为基于粒子群优化的目标适应度函数。ITAE的数值越小,表示控制的系统性能越好,其指标格式一般为:

在进给伺服系统中,误差e(t)指位置跟踪误差。
3.3 粒子群算法优化过程
首先,对粒子群移动范围进行合理设定,粒子表示PID控制器的参数;其次,完成相应算法程序的编写,随机产生初始粒子群,并在Matlab/Simulink中运行被控系统仿真模型得到相应的性能指标(适应度值),根据式(4)计算并更新粒子的速度、位置;最后,对迭代次数与终止条件是否满足进行判断,决定是否再次循环。
4 仿真结果及分析
为了测试粒子群算法优化的前馈PID控制器的动态性能,根据单轴伺服驱动PID控制器控制原理,在Matlab中搭建Simulink仿真模型,如图5所示。根据粒子群算法编写程序文件,搭建粒子群算法优化带前馈的PID控制器的Simulink仿真模型,如图6所示。C轴和X轴输入信号均取x(t)=sin(t)的正弦信号,仿真时间设为6.28 s。C轴与X轴驱动轴基本参数,如表1所示。

表1 C轴与X轴驱动轴基本参数

图5 传统PID控制器仿真模型

图6 基于粒子群算法优化带前馈PID控制器仿真模型
经计算,设置C轴和X轴初始带前馈PID控制参数,如表2所示。
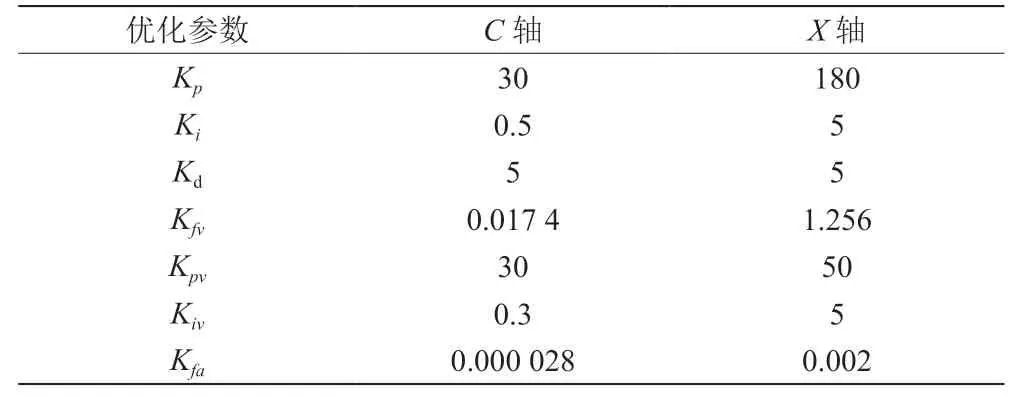
表2 初始带前馈PID控制参数
粒子群算法参数设定:惯性权重ω=0.9;学习因子为C1=C2=2;维 数 为7(有Kp、Ki、Kd、Kfv、Kpv、Kiv、Kfa这7个待优化参数);粒子群规模在此次课题研究中将其设定为100;最大迭代次数将其设定为200;速度范围为 [-1,1],C轴7个待优化参数的搜索区间分别为[0,50]、 [0,0.2]、[0,5]、[0,0.02]、[0,50]、[0,15]、[0,0.02]。X轴7个待优化参数的搜索区间分别为[0,300]、[0,5]、[0,5]、 [0,0.02]、[0,200]、[0,15]、[0,0.02]。其中,非线性摩擦值Tc=0.016(通过对进给驱动系统进行无偏差参数辨识得到[12])。
通过在Matlab/Simulink中迭代仿真,得到优化后的控制参数,如表3所示。C轴和X轴的适应度函数迭代曲线分别如图7和图8所示。
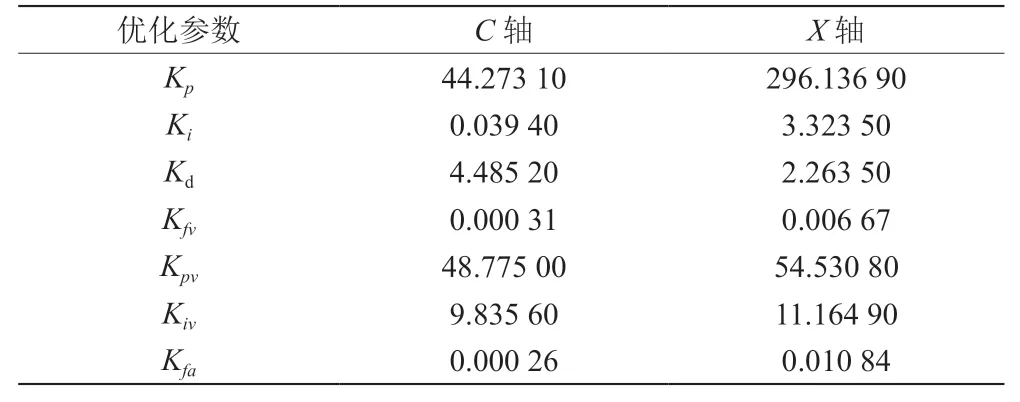
表3 经粒子群算法优化后PID控制参数
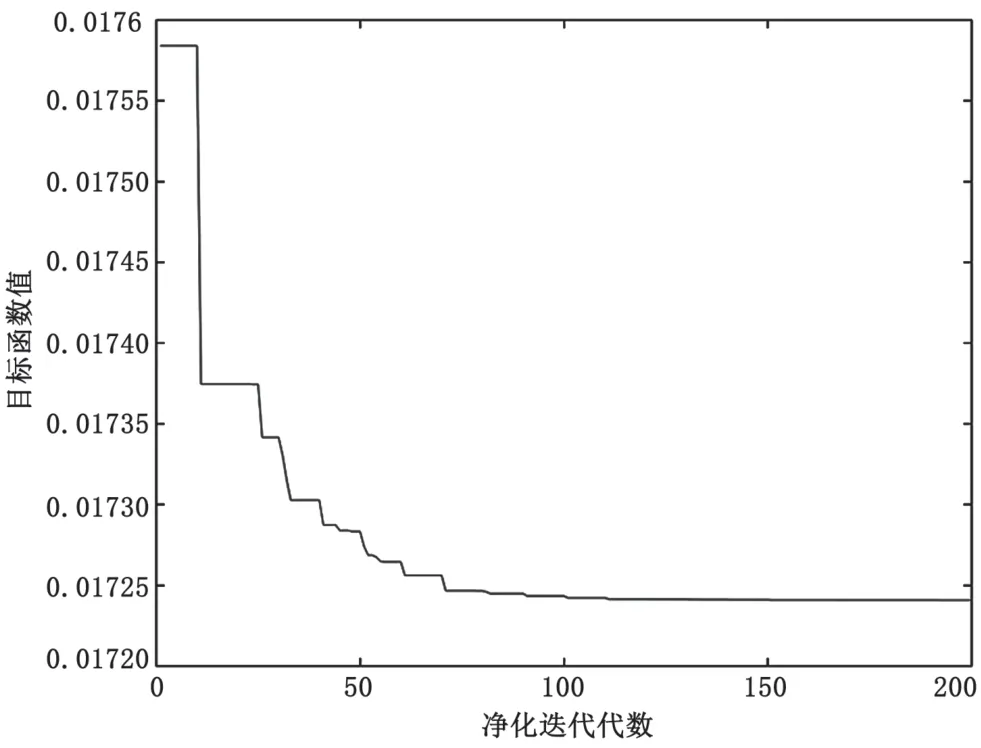
图7 C轴适应度函数的迭代曲线图

图8 X轴适应度函数的迭代曲线图
C轴PID控制器正弦响应曲线、跟踪误差图分别如图9和图10所示,C轴粒子群优化前馈PID控制器的正弦响应曲线、跟踪误差图分别如图11和图12所示。
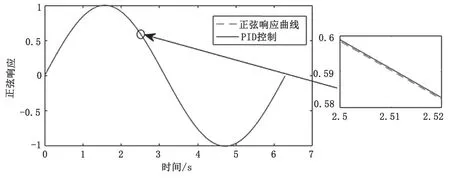
图9 C轴PID控制器正弦响应曲线
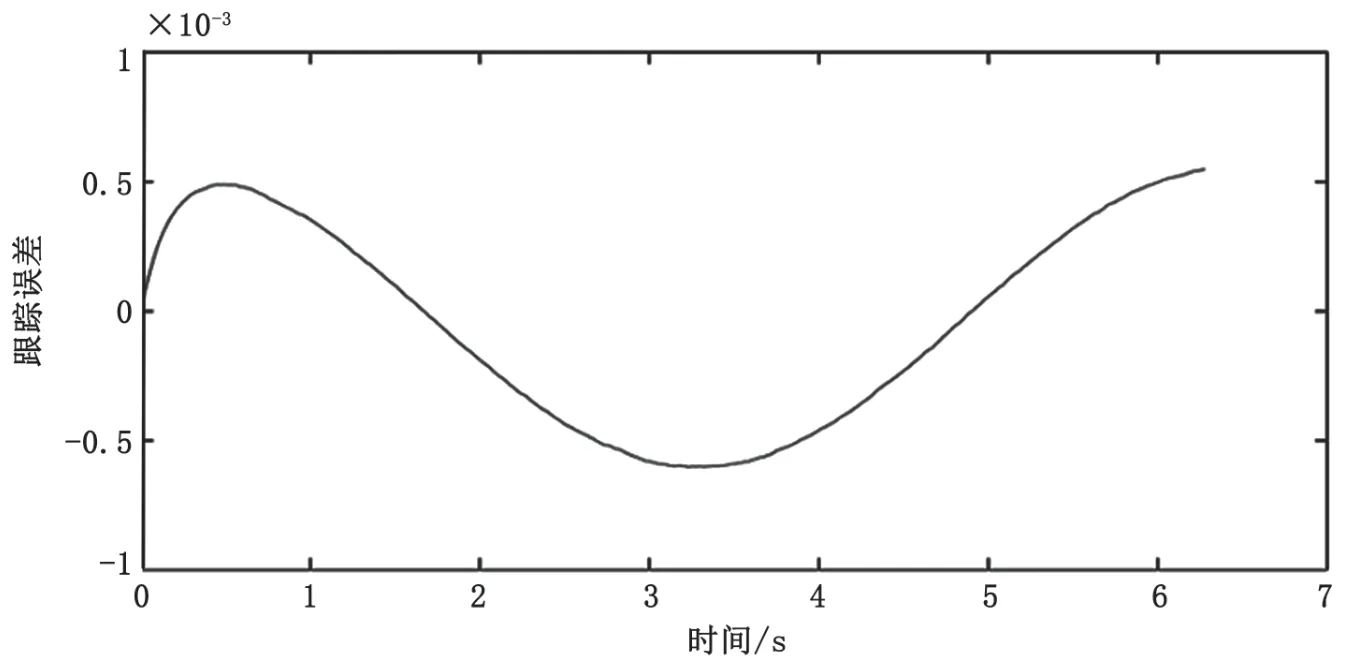
图10 C轴PID控制器正弦跟踪误差图
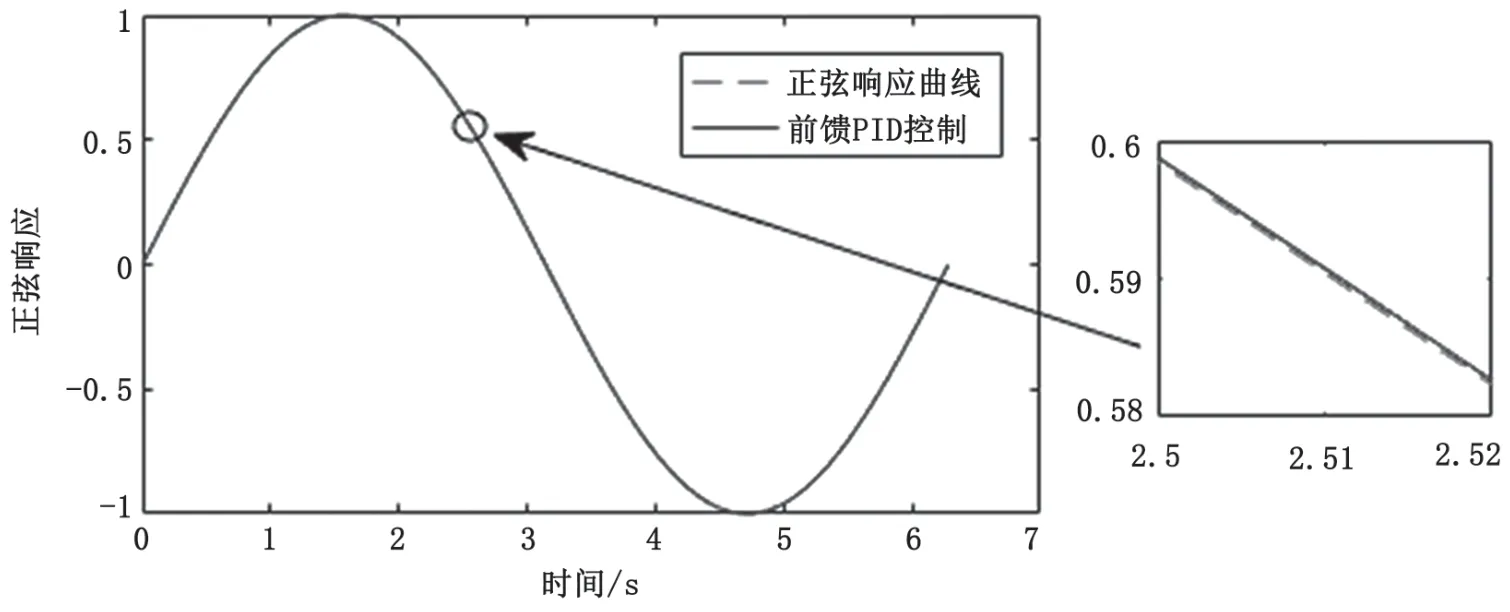
图11 C轴粒子群优化前馈PID控制器的正弦响应曲线
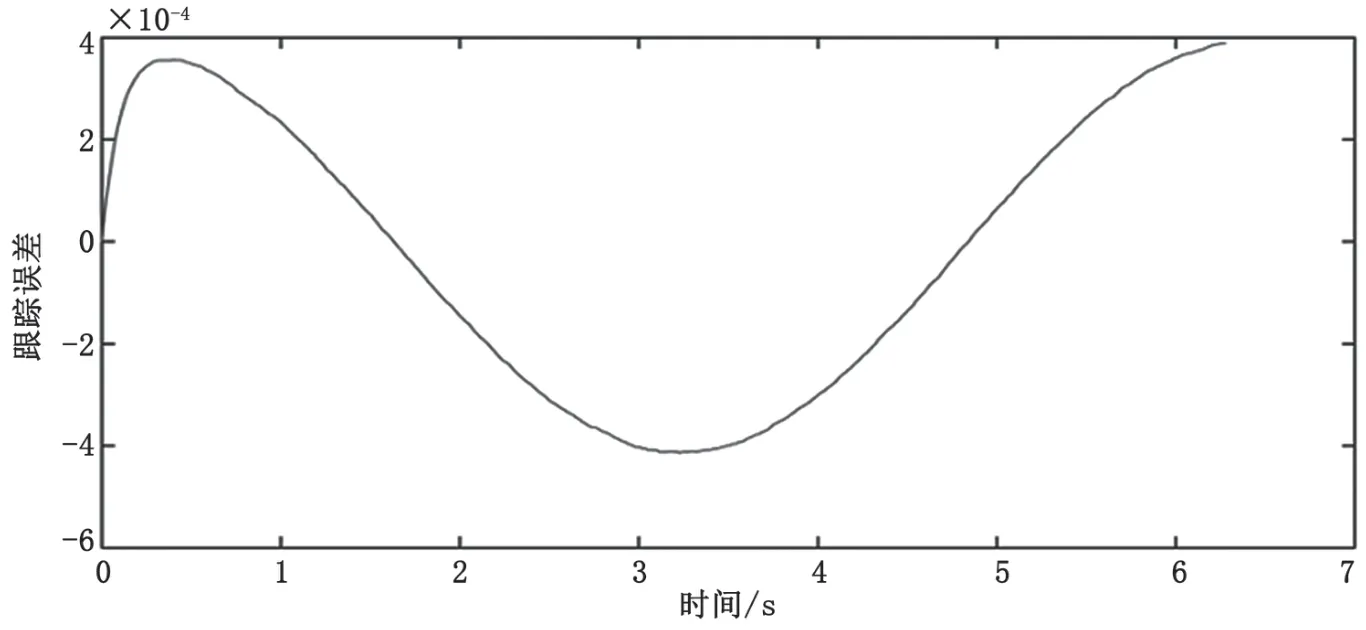
图12 C轴粒子群优化前馈PID控制器的正弦跟踪误差图
X轴PID控制器正弦响应曲线、跟踪误差图分别如 图13和图14所示,X轴粒子群优化前馈PID控制器的正弦响应曲线、跟踪误差图分别如图15和图16所示。
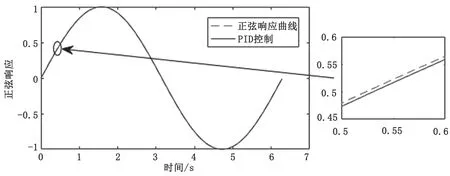
图13 X轴的PID控制器正弦响应曲线与跟踪误差图

图14 X轴的PID控制器正弦响应曲线与跟踪误差图
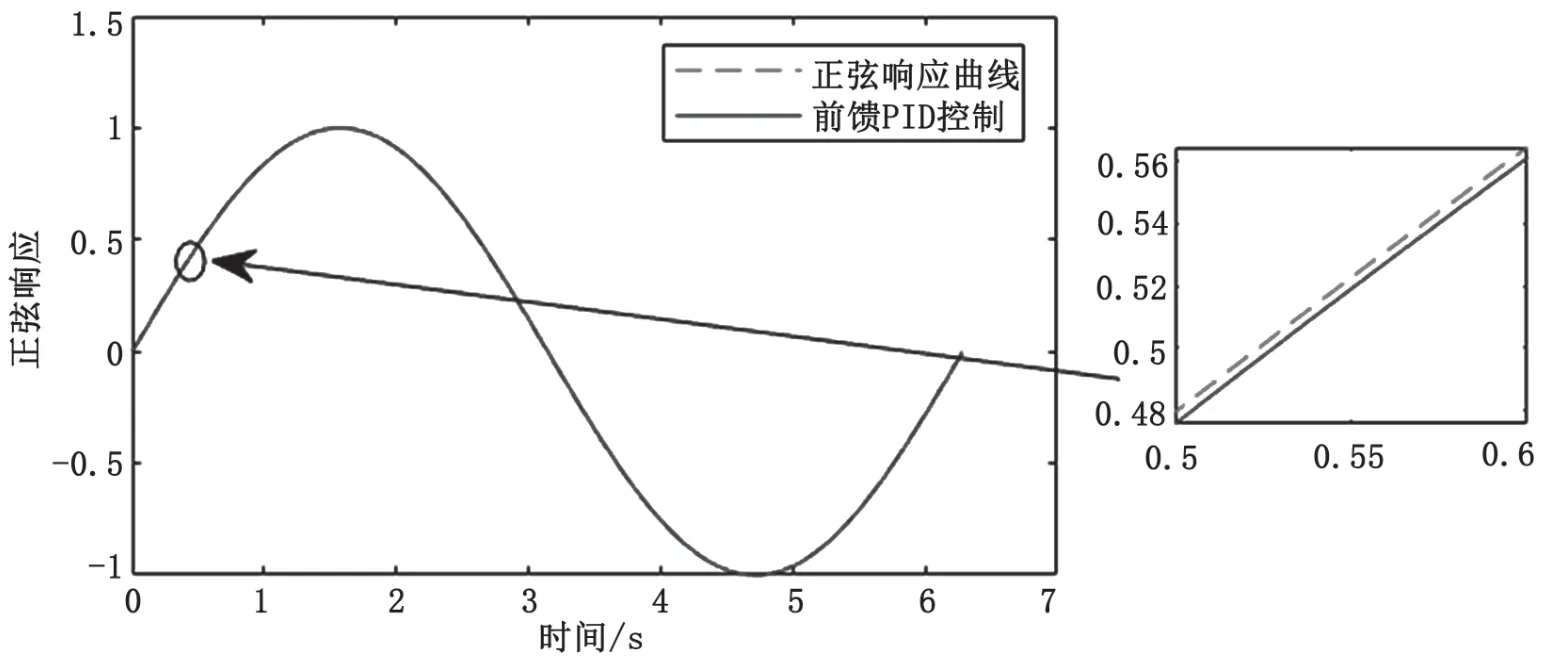
图15 X轴粒子群优化前馈PID控制器的正弦响应曲线
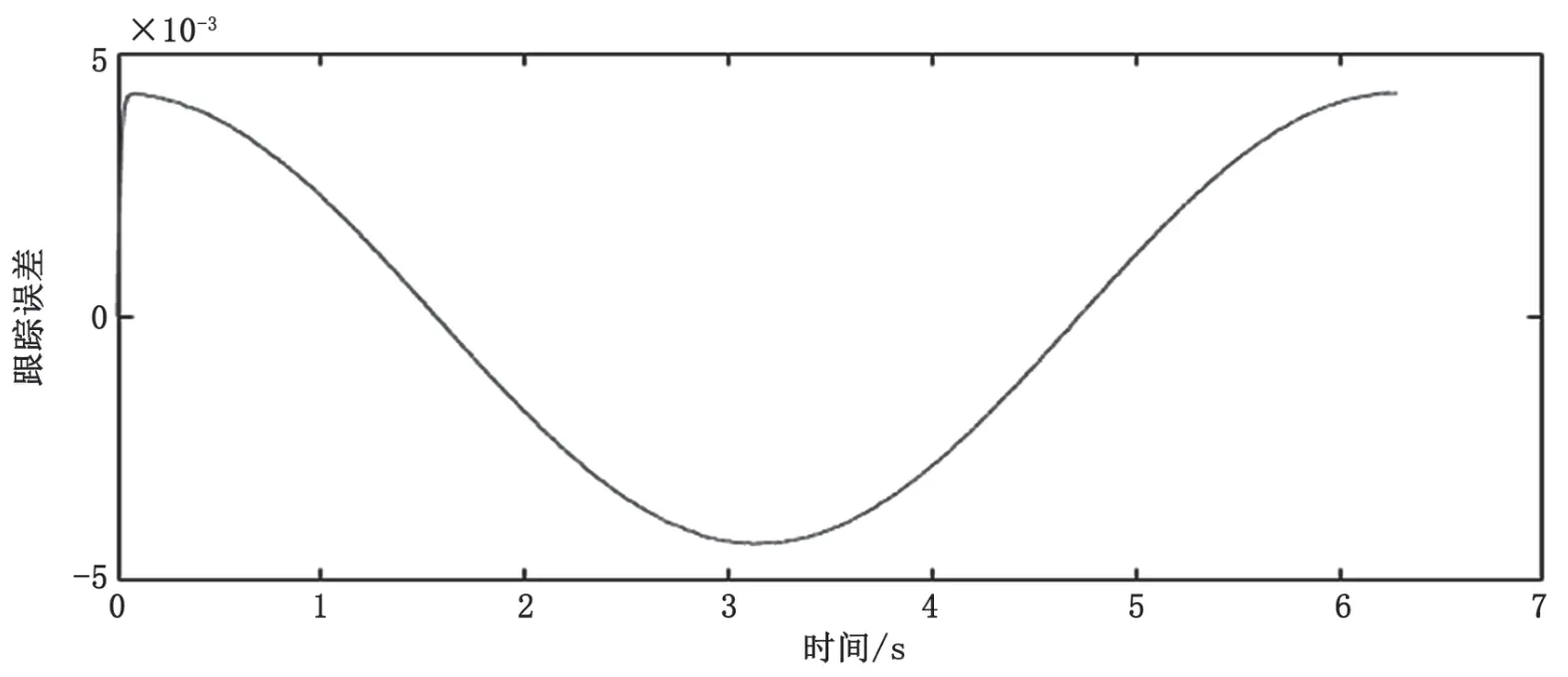
图16 X轴粒子群优化前馈PID控制器的正弦跟踪误差图
经200次迭代后,C轴和X轴经过粒子群优化前馈PID控制的跟踪误差接近正弦状。通过传统PID控制和粒子群优化前馈PID控制的跟踪误差仿真结果对比得知,C轴的跟踪误差值由5.85×10-4rad下降到3.96×10-4rad,X轴的跟踪误差值由7.2 μm下降到4.36 μm,粒子群优化的前馈PID控制明显减小了系统的跟踪误差,提高了系统的跟踪性能。
5 结语
本文研究了基于粒子群算法优化数控滚齿机床工件轴和径向进给轴控制器参数的方法,构建了前馈与反馈相结合的伺服系统控制模型并进行了仿真,验证了此方法可以减少工件轴和径向进给轴的跟踪误差,提高两轴的跟踪性能,获得了较好的控制效果。

