塔里木河干流河段河道整治工程冲刷数值模拟
金庆日
(塔里木河流域干流管理局,新疆库尔勒841000)
0 引言
洪水是导致地形地貌变化和坡面侵蚀形成的主要原因[1],这些大多是人类无法控制的因素。每年6月至9月,我国部分流域受到季风的影响,降雨量陡增,平均降雨量可达1 800 mm/a[2,3]。丰富的水资源仍未得到充分利用,反而频繁的洪水造成了严重的灾难,流域内的一些地区不断受到河岸侵蚀和洪水的破坏[4]。下垫面的复杂构造和季风性降雨会导致河中的水流存在不稳定性,因此对于洪水的形成,预报的难度较大[5]。但是可以通过物理模型和数值模拟对河流平衡冲刷深度进行预测,从而设计出合适的河道整治建筑物,进一步抵御侵蚀继续发展[6]。
1 研究区概况
塔里木河全长2 179 km,由叶尔羌河、和田河、喀什噶尔河、阿克苏河等汇合而成,由于来自冰山的融水含沙量大,河床很不稳定,被称为“无缰的野马”。位于阿克苏地区农一师阿拉尔市的塔里木河大桥,1995年建成,全长605 m,引道长673 m,是开发塔里木石油的第一座大桥,是通向塔克拉玛干大沙漠的必经之桥,为塔里木河上游与中下游的分界点。塔里木河不仅是中国最大的内流河,其河道的横截面和平面几何形状在洪水的作用下多年来不断变化,河道几次改变了路线。北岸由相对较硬的粘性物质组成,而南岸是由松散的物质组成的,这种物质极易被侵蚀,需要修建河道整治工程(RTW),以修复桥梁交叉处的岸线,尤其是南岸部分。
预计在项目使用寿命内,河道将向南迁移,在这种情况下,沿南护岸坡脚的最大冲刷深度可能超过65 m。本文采用该冲刷深度评估两种形态动力学模型的模拟能力。
2 塔里木大桥介绍
2.1 水力要素
通过查阅塔里木河流域干流管理局现有的资料、历年《新疆维吾尔自治区水文年鉴》中与塔里木河阿拉尔段径流、水文相关的部分,经过统计,历年桥址的岸滩流量在60 000~90 000 m3/s之间变化,平均约为75 000 m3/s。大桥附近主要流量与水位情况见表1。由于水位流量曲线呈现较大的分散性,因此,表1中的水位视为平均值。100年一遇的洪水估计为128 000 m3/s,考虑到气候变化的潜在影响,将其设计为148 000 m3/s,用作桥梁工程的设计洪水。

表1 大桥附近主要流量与水位情况
桥址附近的平均坡度为0.000 05(5 cm/km)。在2009年,汛期测量桥梁交叉口周围几个横断面上的水深和流速,当时岸边的流速为76 000 m3/s,测得的平均水深和流速分别为11 m和1.4 m/s,而相应的最大值分别为25 m和2.5 m/s。桥梁段100年重现期的平均流速估计为4.6 m/s。
2.2 河道整治工程
河道整治工程是保证桥梁稳定过水的必要条件也是物理模型试验的重点。南岸由易受侵蚀的松散冲积矿床组成,如果没有河道整治建筑物,南岸很容易受到侵蚀。建议沿南岸设置8.0 km长的导向护岸作为河道整治工程,护岸从桥的上游延伸7.2 km,从桥的下游延伸0.8 km。通过物理模型和两类数值模型进行冲刷等级模拟,每种方法都有其优缺点,使用多种方法并对照实测数据,识别出了一种较优越的方法。
3 河道整治工程冲刷的物理模型
设置4个动床物理模型,分别研究局部桥墩冲刷、对河道整治建筑物的冲刷和土工袋下水的冲刷。其中2个物理模型模拟河道整治建筑物的冲刷见表2。物理模型以大桥为边界,分别模拟上下游7.2 km和0.8 km的来水情况,来水条件模拟百年设计洪水的流速,所用的轻型砂与天然砂的比重为1∶2。表2中的试验组模型尺寸是天然河床的缩略版,采用相同的设计洪水流速,为了修正流速带来的试验结果影响,用降低河床坡比的方式对其进行修正。
河床被天然沉积物覆盖,平均粒径为0.1 mm。测试的水流条件是多年平均流量和百年一遇洪水。研究发现,来水对局部桥墩的冲刷影响不大,桥墩并没有明显的损坏程度;但当河流以45°角冲击南岸河道整治工程时,情况最为不利。在此情况下,防洪堤坝脚处出现了凹陷,同时在防洪堤下部会形成一个深的冲刷坑。冲刷坑中的最低河床高程在-51~-61 m之间变化。由此可见,洪水对河道整治建筑物与土工袋下水的危害比较严重。

表2 原河床和试验河床对照表
试验组断面中上游平均流速在3.0~3.5 m/s之间变化,当水流经过弯曲的河道整治工程时,将增加到4.3~4.6 m/s,类似于百年一遇洪水的流速。流速的增加导致了道整治工程周围局部冲刷的加剧,特别是在凸起防洪堤头部附近,这也是在原河床模型中观察到的。剖面模型中测量的最小河床高程在标高之间变化如图1所示。
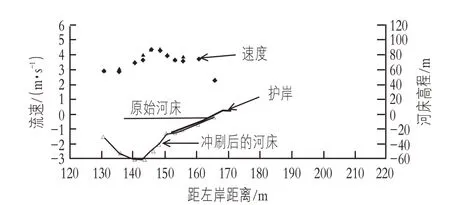
图1 河道冲刷横截面测量示例图
物理模型试验表明,尽管流量、输沙方式会影响冲刷破坏的发展速率,但它们对平均流量下的冲刷没有显著影响。
4 数值模型设置
物理模型显示,当水流沿南岸集中时,将出现对南岸河道整治工程最不利的条件,因此数值模型也设置了这些水流条件。数值模型中保留了物理模型中沿南岸的水流线形、几何形状和弯道。模型中引入了一个与南岸平行的虚拟北岸,以保持恒定的河道宽度,避免人为因素导致的收缩效应。模型包括主河道、部分邻近洪泛区、导向护岸、高防洪堤和一段引道。数值模型长8.0 km,主河道宽230 m。对河道冲刷数值模型进行网格划分见图2,在4 023个节点中设置7 587个三角形元素,除了凸起的堤岸附近,节点之间的距离减少到1 m。
在泥沙输移计算中,假定河床被均匀的0.1 mm泥沙覆盖,运输率是用恩格尔隆德-汉森方程计算的。护岸的边坡比假定为1∶1,边界条件:上游部分的流量为148 000 m3/s,并假设泥沙流入处于平衡状态,即通过泥沙输移方程计算。

图2 河道冲刷数值模型网格划分
使用T2D和R2D两个形态动力学模型来模拟河道整治工程冲刷。这两个模型使用的是非结构化网格,设定了相同的网格和边界条件。对于湍流模型而言,R2D使用了一个简单的方程模型,该模型假设涡流粘度与当地水深和剪切速度的乘积成比例;而T2D使用的是双方程k-ε湍流模型。
5 结果分析
5.1 流体力学
在形态动力学模拟开始之前,通过两个流体动力学模型计算的标量速度场的对比情况见图3。尽管使用了相同的网格、粗糙度和边界条件,但两个模型预测的速度场并不相同。
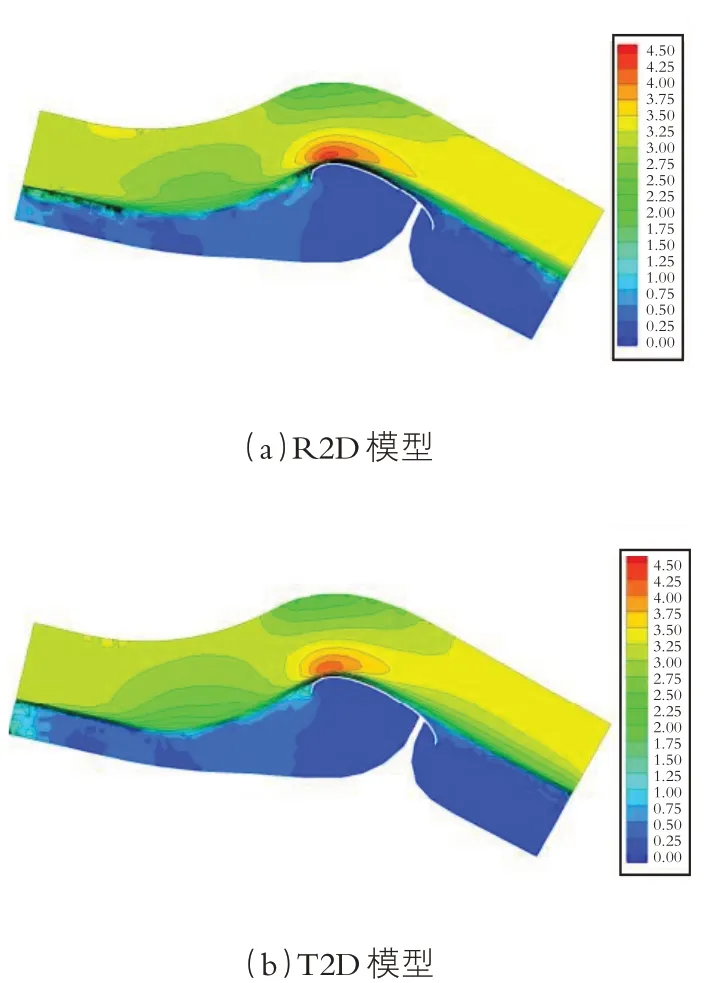
图3 初始速度场分布情况
在断面模型中观察到的范围内,两个模型中计算的流入速度均为3.1 m/s。两个模型都预测最高局部速度出现在防洪堤的上游,即河岸整治建筑的最大曲率位置,见图3。R2D预测峰值速度为4.3 m/s,而T2D预测为4.2 m/s,物理模型也呈现了这个结果。由于T2D模拟系统相当复杂,开始模拟之前需要设置几个数值选项(例如边界条件处理、摩擦定律、湍流模拟、平流类型等)。为了获得图3所示的T2D结果,需要对输入参数进行大量的测试和更改。在这种特殊情况下,使用T2D的默认选项进行模拟并不能产生真实的速度分布。相比之下,R2D的设置相对简单,只使用了默认选项。
5.2 形态动力学
在计算初始速度场后,将模型与形态动力学模块相结合,进一步预测河床随时间的变化。在50 d后达到最大冲刷深度,通过形态动力学模型计算的河床水位见图4。

图4 50 d后通过形态动力学模型计算的河床水位
位于凸起防洪堤顶部的横断面(垂直于水流)上的河床高程如图5所示。两种模型预测的初始冲刷率相似;30 d后,两个模型都产生了相同的现象。但是,此后T2D模型不再继续冲刷,护岸坡脚处的最小河床高程保持在-50 m。相比之下,R2D的河床水位持续下降,50 d后达到-60 m,此后保持不变。
两种模型预测的冲刷坑位置和形状相似,并且都处在局部水流速度高的位置,而R2D模拟结果中产生了更深的冲刷坑,这与物理模型中的观察结果更为一致。
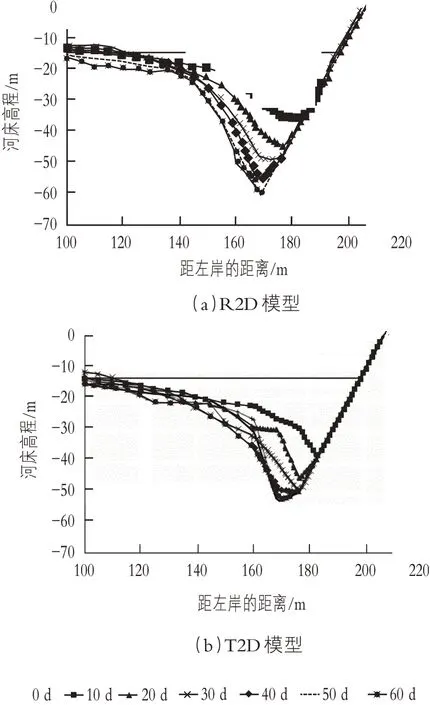
图5 凸起防洪堤上游段河床演变
6 结语
文中用形态动力学模型R2D和T2D预测塔里木河大桥南河岸整治工程,冲刷坑的形状和位置与物理模型中观察到的一致,但R2D能更好地模拟冲刷坑的深度,与物理模型结果一致,而T2D预测的结果要小15%。结合本文的研究可以得出,二维数值模拟是预测河流平均冲刷深度的一个有效手段。模型具有较强的适用性,能够很好地模拟河道冲刷的计算,可以为防汛抗旱工作提供数据支撑。但不同的数值模型可能产生不同的冲刷模拟结果,出于设计目的,将数值模型与其他方法(如分析方法、现场观测或物理模型)结合或相互验证对于提升精度是很有必要的。

