浅析我国几种常用测量坐标系与坐标转换方法

毕研磊

（信阳市水利勘测设计院，河南 信阳 464000）

0 引言

坐标系作为测量中的一部分，一直是测量中最核心、最基本的问题。任何物体的空间表达都体现在坐标上，所以它是测量的基础。1949年以来，我国陆续更新了三次坐标基准，每次坐标系统的更新，其椭球参数都有较大变化（如坐标系原点、长半轴、扁率等），这造成同一点坐标值会不同程度改变，所以每次测绘基准的更新势必关系到坐标转换，以保证新旧测绘成果之间的无损变换。近些年随着GNSS卫星导航定位技术的飞速发展，GNSS-RTK技术广泛应用于测绘中，但是GNSS卫星定位技术一般提供的是WGS-84坐标，为了得到我们所需要的坐标系坐标，也需通过坐标转换来实现。坐标转换一般包括两种形式：①同一基准下的坐标转换，比如同一基准下空间直角坐标与经纬度坐标的转换、或者是经纬度坐标与高斯平面坐标之间的转换；②不同基准下的坐标转换，即不同参考椭球下，各种坐标之间的转换，这种坐标转换常用到莫洛金斯基三参数、平面四参数、布尔莎七参数等方法。由于同一基准下的坐标转换有固定的公式，而且转换精度较高，我们这里不做探讨，本文主要介绍不同基准下的坐标转换问题。

1 我国常用测量坐标系简介

1.1 北京54坐标系

1949年，我国开始大规模的工程建设活动，由于当时测绘资料不足以及技术条件的限制，我国还未有自己的坐标系统。为满足国民经济和国防建设的需要，我们利用前苏联在东北地区建立的一等三角锁，分别向东南地区、中部地区、西北地区进行延伸，然后进行局部平差，建立起我国第一代测量坐标系统——1954北京坐标系，该坐标系相当于前苏联1942普尔科沃坐标系在我国的延伸。由于其参考椭球面是与苏联的大地水准面最佳拟合，而我国的坐标是在其坐标原点逐级推算过来，随着距离的增加，推算过程也会造成误差积累，这就导致该参考椭球面与我国水准面符合性越来越差；且当时1954北京坐标系仅进行局部三角网的平差，这也造成坐标值存在较大误差。

1.2 西安80坐标系（GDZ80）

1980西安大地坐标系是我国建立的第二代测量坐标基准，该坐标系弥补了北京54坐标系中的诸多不足，如坐标轴指向不明确、参考椭球与我国的大地水准面符合较差以及没有进行全国三角网整体平差等问题，这些问题都会影响坐标的精度。为保证平面坐标我国的准确性，西安80坐标系遵循以下几点原则进行建立：①大地原点必须选在我国内部（最终确定为西安市泾阳县永乐镇）；②选用国际最为前沿的椭球参数；③基于最小二乘原理保证全国范围内椭球高与正常高的差值（即高程异常值）最小；④三角网除了局部平差外，还应在全国范围完成系统平差；⑤基准面选用近30年青岛验潮站的水准成果（1985国家高程基准）。经以上原则建立起的西安80坐标系，其坐标精度大幅提高，并且系统误差明显减小，为我国之后的国防、经济建设奠定了深厚的测量基础。

1.3 国家2000坐标系（CGCS2000）

参心坐标系一般是基于传统大地测量计算得来，其坐标表现形式为高斯投影得到的二维平面坐标，高程一般是通过水准来获取。当地球上两点距离较远时，利用此坐标系计算的空间距离会引起较大误差。随着空间技术的发展，尤其是全球范围GNSS导航定位技术的发展，如何获取全球高精度的三维地心坐标成为我们关注的要点，所以我国迫切需要建立高精度的地心坐标系。在这种背景下2008年我国建立新一代地心测量坐标系——CGCS2000，经过近十几年的发展，国家2000坐标系已广泛应用到水利、交通、航天、海洋等各个工程领域，为我国的经济建设带来巨大帮助。

我国现行的坐标系主要为以上三种，也有部分城市建立的独立坐标系，各种坐标系椭球参数对比如表1所示。

表1 我国常用坐标系椭球参数对比

2 不同基准坐标转换方法

测量工作中，我们经常遇到坐标转换问题，尤其是不同基准下的坐标转换，其关键是确定数学模型和转换参数。数学模型即为我们常用的三参数、四参数以及布尔莎七参数等模型；数学模型确定后，再利用公共点计算参数建立不同坐标系之间的关系，目前常用的参数计算方法为最小二乘原理；最后利用转换参数对其他待求点进行转换。由于整个计算过程较为烦琐，一般需要在计算机上完成计算。以下简单介绍三种转换模型：

2.1 莫洛琴斯基三参数

三参数模型是假定不同基准的两种坐标系其坐标轴指向是一样的，只需要对坐标轴进行平移即可完成坐标系转换，所以该模型只有三个平移参数，即X轴平移、Y轴平移、Z轴平移。由于该模型是在空间直角坐标系下进行建立的，所以求解参数前需将两个基准下的坐标转换为空间直角坐标，再进行三参数计算，参数计算完毕即建立了两种坐标系的关系。正常情况三参数计算只需1个公共点，但为了校核参数，最好选用两个或两个以上的公共点计算。其模型计算公式见式（1）：

式中：（X，Y，Z）-目标坐标系空间直角坐标；（X0，Y0，Z0）-待转换坐标系空间直角坐标；（ΔX，ΔY，ΔZ）分别表示X轴平移、Y轴平移与Z轴平移。由于该模型只进行了平移变换，所以该模型一般适用于范围较小（一般在3～5km以内）的工程。

2.2 平面四参数

四参数模型是基于平面直角坐标系的转换模型，求解参数前需将公共点转换至本基准下的高斯投影坐标，再对待求点坐标经平移、旋转以及尺度变换转换至目标坐标系。该模型包含四个参数：分别为x轴平移、y轴平移、坐标轴旋转以及尺度变换，该方法需要求解四个参数，由于一个公共点只能建立两个方程，所以至少需要两个公共点，其模型计算公式见式（2）：

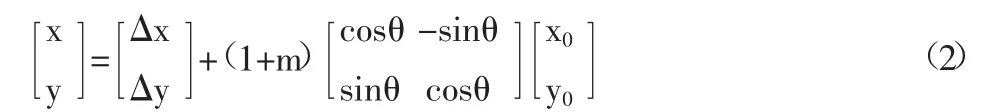
式中：（x，y）-目标坐标系平面坐标；（x0，y0）-原坐标系平面坐标；（Δx，Δy）-平移参数；θ-旋转参数；m-尺度变换参数。四参数模型不仅进行平移变换，还对坐标轴进行旋转和尺度缩放，其精度有所提高，但该模型是投影到平面进行的坐标变换，所以这种模型也只适用于中小范围（一般在5～7km以内）的工程区域。

2.3 布尔莎七参数

与莫洛琴斯基三参数模型类似，布尔莎七参数模型也是基于空间直角坐标系的转换模型，所以计算参数需将两种基准下的坐标转换为空间直角坐标。不同的是七参数模型除了对坐标系进行平移外，还对三个坐标轴进行旋转变换，以及空间尺度缩放，这里需要求解七个参数。由于一个公共点可以列出三个方程，所以七个参数至少需要三个公共点求解。坐标转换模型公式见式（3）：

式中：（X，Y，Z）-目标坐标系空间直角坐标；（X0，Y0，Z0）-待求点坐标系空间直角坐标；（ΔX，ΔY，ΔZ）-三个平移参数；（εx，εy，εz）-三个旋转参数；m-尺度变换参数。七参数模型是在空间直角系下的转换模型，又同时考虑了旋转和尺度两个因素，相较于三参数、四参数其模型精度更高。所以七参数模型常用于范围较大（一般在10km以上）的工程区域，确保待求点的转换精度。

3 结语

通过理论分析并经大量实践证明，三参数、四参数模型一般适用于中小范围（一般在5～7km以内）的工程区域，对于跨度范围较大的工程（如公路、电力、河道等工程），为保证坐标精度，常用布尔莎七参数模型建立转换关系。目前常用的坐标转换工具较多，比如笑脸工具、Coord、Proj等商业软件都是比较成熟的坐标转换工具，且包含目前常用的莫洛金斯基三参数、平面四参数以及布尔莎七参数等转换方法。一些GNSS数据处理软件（如HGO、TGO、SGO等软件）也包含坐标转换工具插件，这为测绘工作者带来很大便利。本文简单介绍我国常用的三种坐标系，并从理论方面浅析其坐标转换方法，以期帮助测绘人员更深层次理解坐标转换原理。